3.2: Solve Percent Applications
- Last updated
- Save as PDF
- Page ID
- 30378
Learning Objectives
By the end of this section, you will be able to:
- Translate and solve basic percent equations
- Solve percent applications
- Find percent increase and percent decrease
- Solve simple interest applications
- Solve applications with discount or mark-up
Be prepared
Before you get started, take this readiness quiz.
- Convert 4.5% to a decimal.
If you missed this problem, review [link]. - Convert 0.6 to a percent.
If you missed this problem, review [link]. - Round 0.875 to the nearest hundredth.
If you missed this problem, review [link]. - Multiply (4.5)(2.38).
If you missed this problem, review [link]. - Solve 3.5=0.7n.
If you missed this problem, review [link]. - Subtract 50−37.45.
If you missed this problem, review [link].
Translate and Solve Basic Percent Equations
We will solve percent equations using the methods we used to solve equations with fractions or decimals. Without the tools of algebra, the best method available to solve percent problems was by setting them up as proportions. Now as an algebra student, you can just translate English sentences into algebraic equations and then solve the equations.
We can use any letter you like as a variable, but it is a good idea to choose a letter that will remind us of what you are looking for. We must be sure to change the given percent to a decimal when we put it in the equation.
Example \(\PageIndex{1}\)
Translate and solve: What number is 35% of 90?
Solution
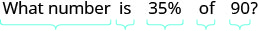 |
|
| Translate into algebra. Let n= the number. | 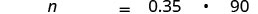 |
| Remember "of" means multiply, "is" means equals. | |
| Multiply. | 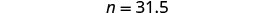 |
| 31.5 is 35% of 90 |
Try It \(\PageIndex{2}\)
Translate and solve:
What number is 45% of 80?
- Answer
-
36
Try It \(\PageIndex{3}\)
Translate and solve:
What number is 55% of 60?
- Answer
-
33
We must be very careful when we translate the words in the next example. The unknown quantity will not be isolated at first, like it was in Example. We will again use direct translation to write the equation.
Example \(\PageIndex{4}\)
Translate and solve: 6.5% of what number is $1.17?
Solution
 |
|
| Translate. Let n= the number. | 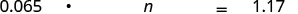 |
| Multiply. | 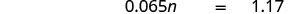 |
| Divide both sides by 0.065 and simplify. |  |
| 6.5% of $18 is $1.17 |
Try It \(\PageIndex{5}\)
Translate and solve:
7.5% of what number is $1.95?
- Answer
-
$26
Try It \(\PageIndex{6}\)
Translate and solve:
8.5% of what number is $3.06?
- Answer
-
$36
In the next example, we are looking for the percent.
Example \(\PageIndex{7}\)
Translate and solve: 144 is what percent of 96?
Solution
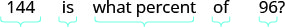 |
|
| Translate into algebra. Let p= the percent. | 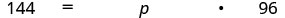 |
| Multiply. |  |
| Divide by 96 and simplify. |  |
| Convert to percent. |  |
| 144 is 150% of 96 |
Note that we are asked to find percent, so we must have our final result in percent form.
Try It \(\PageIndex{8}\)
Translate and solve:
110 is what percent of 88?
- Answer
-
125%
Try It \(\PageIndex{9}\)
Translate and solve:
126 is what percent of 72?
- Answer
-
175%
Solve Applications of Percent
Many applications of percent—such as tips, sales tax, discounts, and interest—occur in our daily lives. To solve these applications we’ll translate to a basic percent equation, just like those we solved in previous examples. Once we translate the sentence into a percent equation, we know how to solve it.
We will restate the problem solving strategy we used earlier for easy reference.
USE A PROBLEM-SOLVING STRATEGY TO SOLVE AN APPLICATION.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Now that we have the strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications will involve everyday situations, you can rely on your own experience.
Example \(\PageIndex{10}\)
Dezohn and his girlfriend enjoyed a nice dinner at a restaurant and his bill was $68.50. He wants to leave an 18% tip. If the tip will be 18% of the total bill, how much tip should he leave?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the amount of tip should Dezohn leave |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let t = amount of tip. |
| Step 4. Translate into an equation. | 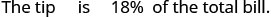 |
| Write a sentence that gives the information to find it. |  |
| Translate the sentence into an equation. | 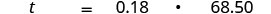 |
| Step 5. Solve the equation. Multiply. | 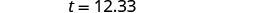 |
| Step 6. Check. Does this make sense? | |
| Yes, 20% is close to 18%, and 20% of $70 is $14. | |
| Step 7. Answer the question with a complete sentence. | Dezohn should leave a tip of $12.33. |
Try It \(\PageIndex{11}\)
Cierra and her sister enjoyed a dinner in a restaurant and the bill was $81.50. If she wants to leave 18% of the total bill as her tip, how much should she leave?
- Answer
-
$14.67
Try It \(\PageIndex{12}\)
Kimngoc had lunch at her favorite restaurant. She wants to leave 15% of the total bill as her tip. If her bill was $14.40, how much will she leave for the tip?
- Answer
-
$2.16
Example \(\PageIndex{13}\)
The label on Masao’s breakfast cereal said that one serving of cereal provides 85 milligrams (mg) of potassium, which is 2% of the recommended daily amount. What is the total recommended daily amount of potassium?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the total amount of potassium that is recommended |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let a= total amount of potassium. |
| Step 4. Translate. Write a sentence that gives the information to find it. |  |
| Translate into an equation. | 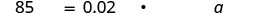 |
| Step 5. Solve the equation. |  |
| Step 6. Check. Does this make sense? | |
| Yes, 2% is a small percent and 85 is a small part of 4,250. | |
| Step 7. Answer the question with a complete sentence. | The amount of potassium that is recommended is 4,250 mg. |
Try It \(\PageIndex{14}\)
One serving of wheat square cereal has seven grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?
- Answer
-
25 grams
Try It \(\PageIndex{15}\)
One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?
- Answer
-
2,375 mg
Example \(\PageIndex{16}\)
Mitzi received some gourmet brownies as a gift. The wrapper said each brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the percent of the total calories from fat |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let p= percent of fat. |
| Step 4. Translate. Write a sentence that gives the information to find it. |  |
| Translate into an equation. | 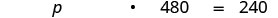 |
| Step 5. Solve the equation. |  |
| Divide by 480. |  |
| Put in a percent form. |  |
| Step 6. Check. Does this make sense? | |
| Yes, 240 is half of 480, so 50% makes sense. | |
| Step 7. Answer the question with a complete sentence. | Of the total calories in each brownie, 50% is fat. |
Try It \(\PageIndex{17}\)
Solve. Round to the nearest whole percent.
Veronica is planning to make muffins from a mix. The package says each muffin will be 230 calories and 60 calories will be from fat. What percent of the total calories is from fat?
- Answer
-
26%
Try It \(\PageIndex{18}\)
Solve. Round to the nearest whole percent.
The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat?
- Answer
-
40%
Find Percent Increase and Percent Decrease
People in the media often talk about how much an amount has increased or decreased over a certain period of time. They usually express this increase or decrease as a percent.
To find the percent increase, first we find the amount of increase, the difference of the new amount and the original amount. Then we find what percent the amount of increase is of the original amount.
FIND THE PERCENT INCREASE.
- Find the amount of increase.
\(\text{new amount }−\text{ original amount }=\text{ increase}\) - Find the percent increase.
The increase is what percent of the original amount?
Example \(\PageIndex{19}\)
In 2011, the California governor proposed raising community college fees from $26 a unit to $36 a unit. Find the percent increase. (Round to the nearest tenth of a percent.)
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the percent increase |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let \(p\) = the percent. |
| Step 4. Translate. Write a sentence that gives the information to find it. | |
| First find the amount of increase. | new amount − original amount = increase |
| 36−26=10 | |
| Find the percent. | Increase is what percent of the original amount? |
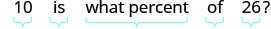 |
|
| Translate into an equation. | 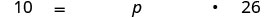 |
| Step 5. Solve the equation. |  |
| Divide by 26. | \(0.3846... = p\) |
| Change to percent form; round to the nearest tenth. | \( 38.5 \% = p \) |
| Step 6. Check. Does this make sense? | |
| Yes, 38.5% is close to \(\frac{1}{3}\), and 10 is close to \(\frac{1}{3}\) of 26. | |
| Step 7. Answer the question with a complete sentence. | The new fees represent a 38.5% increase over the old fees. |
Try It \(\PageIndex{20}\)
Find the percent increase. (Round to the nearest tenth of a percent.)
In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.
- Answer
-
8.8%
Try It \(\PageIndex{21}\)
Find the percent increase.
In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was $2.25.
- Answer
-
50%
Finding the percent decrease is very similar to finding the percent increase, but now the amount of decrease is the difference of the original amount and the new amount. Then we find what percent the amount of decrease is of the original amount.
FIND THE PERCENT DECREASE.
- Find the amount of decrease.
\(\text{original amount }−\text{ new amount }=\text{ decrease}\) - Find the percent decrease.
The decrease is what percent of the original amount?
Example \(\PageIndex{22}\)
The average price of a gallon of gas in one city in June 2014 was $3.71. The average price in that city in July was $3.64. Find the percent decrease.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the percent decrease |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent that quantity. | Let p= the percent decrease. |
| Step 4. Translate. Write a sentence that gives the information to find it. | |
| First find the amount of decrease. | 3.71−3.64=0.07 |
| Find the percent. | Decrease is what percent of the original amount? |
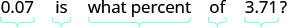 |
|
| Translate into an equation. | 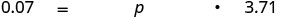 |
| Step 5. Solve the equation. |  |
| Divide by 3.71. | \( 0.0188... = p\) |
| Change to percent form; round to the nearest tenth. |  |
| Step 6. Check. Does this make sense? | |
| Yes, if the original price was $4, a 2% decrease would be 8 cents. | |
| Step 7. Answer the question with a complete sentence. | The price of gas decreased 1.9%. |
Try It \(\PageIndex{23}\)
Find the percent decrease. (Round to the nearest tenth of a percent.)
The population of North Dakota was about 672,000 in 2010. The population is projected to be about 630,000 in 2020.
- Answer
-
6.3%
Try It \(\PageIndex{24}\)
Find the percent decrease.
Last year, Sheila’s salary was $42,000. Because of furlough days, this year, her salary was $37,800.
- Answer
-
10%
Solve Simple Interest Applications
Do you know that banks pay you to keep your money? The money a customer puts in the bank is called the principal, P, and the money the bank pays the customer is called the interest. The interest is computed as a certain percent of the principal; called the rate of interest, r. We usually express rate of interest as a percent per year, and we calculate it by using the decimal equivalent of the percent. The variable t, (for time) represents the number of years the money is in the account.
To find the interest we use the simple interest formula, I=Prt.
SIMPLE INTEREST
If an amount of money, P, called the principal, is invested for a period of t years at an annual interest rate r, the amount of interest, I, earned is
\[\begin{array}{lllll} {} &{} &{I} &{=} &{\text { interest }}\\ {I = Prt} &{\text{where}} &{P} &{=} &{\text { principle }}\\ {} &{} &{r} &{=} &{\text { rate }}\\ {} &{} &{t} &{=} &{\text { time }} \end{array}\]
Interest earned according to this formula is called simple interest.
Interest may also be calculated another way, called compound interest. This type of interest will be covered in later math classes.
The formula we use to calculate simple interest is I=Prt. To use the formula, we substitute in the values the problem gives us for the variables, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
Example \(\PageIndex{25}\)
Nathaly deposited $12,500 in her bank account where it will earn 4% interest. How much interest will Nathaly earn in 5 years?
\[\begin{aligned} I &=? \\ P &=\$ 12,500 \\ r &=4 \% \\ t &=5 \text { years } \end{aligned}\]
Solution
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of interest earned}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for.}} &{\text{Let I = the amount of interest.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{I = (12500)(.04)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{I = 2500} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {\qquad \text{Is } $2,500 \text{ is a reasonable interest} } &{} \\ {\qquad \text{on }$12,500? \text{ Yes.}} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The interest is }$2500} \\ {\text{complete sentence.}} &{} \ \end{array}\)
Try It \(\PageIndex{26}\)
Areli invested a principal of $950 in her bank account with interest rate 3%. How much interest did she earn in 5 years?
- Answer
-
$142.50
Try It \(\PageIndex{27}\)
Susana invested a principal of $36,000 in her bank account with interest rate 6.5%. How much interest did she earn in 3 years?
- Answer
-
$7020
There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we don’t know the rate. To find the rate, we use the simple interest formula, substitute in the given values for the principal and time, and then solve for the rate.
Example \(\PageIndex{28}\)
Loren loaned his brother $3,000 to help him buy a car. In 4 years his brother paid him back the $3,000 plus $660 in interest. What was the rate of interest?
\[\begin{array}{lll} {I} &{=} &{\$ 660} \\ {P} &{=} &{\$ 3000} \\ {r} &{=} &{?} \\ {t} &{=} &{4 \text { years } }\end{array}\]
Solution
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the rate of interest}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. Choose}} &{\text{Let r = the rate of interest.}} \\ {\text{ a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{660 = (3000)r(4)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{660 = (12000)r} \\ {\text{Divide.}} &{0.055 = r} \\ {\text{Change to percent form.}} &{5.5\% = r} \\\\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {I = Prt} &{} \\ {660 \stackrel{?}{=} (3000)(0.055)(4)} &{} \\ {660 = 660\checkmark} &{} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The rate of interest was }5.5\%} \\ {\text{complete sentence.}} &{} \end{array}\)
Notice that in this example, Loren’s brother paid Loren interest, just like a bank would have paid interest if Loren invested his money there.
Try It \(\PageIndex{29}\)
Jim loaned his sister $5,000 to help her buy a house. In 3 years, she paid him the $5,000, plus $900 interest. What was the rate of interest?
- Answer
-
6%
Try It \(\PageIndex{30}\)
Hang borrowed $7,500 from her parents to pay her tuition. In 5 years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of interest?
- Answer
-
4%
Example \(\PageIndex{31}\)
Eduardo noticed that his new car loan papers stated that with a 7.5% interest rate, he would pay $6,596.25 in interest over 5 years. How much did he borrow to pay for his car?
Solution
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount borrowed (the principal)}} \\ {\text{a variable to represent that quantity.}} &{} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{Let P = principal borrowed.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{6596.25 = P(0.075)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{6596.25 = 0.375P} \\ {\text{Divide.}} &{17590 = P} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ {I = Prt} &{} \\ {6596.25 \stackrel{?}{=} (17590)(0.075)(5)} &{} \\ {6596.25 = 6596.25\checkmark} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The principal is }$17590} \\ {\text{complete sentence.}} &{} \ \end{array}\)
Try It \(\PageIndex{32}\)
Sean’s new car loan statement said he would pay $4,866.25 in interest from an interest rate of 8.5% over 5 years. How much did he borrow to buy his new car?
- Answer
-
$11,450
Try It \(\PageIndex{33}\)
In 5 years, Gloria’s bank account earned $2,400 interest at 5%. How much had she deposited in the account?
- Answer
-
$9,600
Solve Applications with Discount or Mark-up
Applications of discount are very common in retail settings. When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price.
We summarize the discount model in the box below.
DISCOUNT
\[\begin{array}{l}{\text { amount of discount }=\text { discount rate } \times \text { original price }} \\ {\text { sale price }=\text { original price - amount of discount }}\end{array}\]
Keep in mind that the sale price should always be less than the original price.
Example \(\PageIndex{34}\)
Elise bought a dress that was discounted 35% off of the original price of $140. What was (a) the amount of discount and (b) the sale price of the dress?
Solution
\(\begin{array} {llll} { \text{(a)} } &{\text{Original price}} &{=} &{$140} \\
&{ \text{ Discount rate}} &{=} &{35\%} \\
&{ \text{ Discount}} &{=} &{?} \end{array}\)
\(\begin{array} {ll} {\textbf{Step 1. Read}} {\text{ the problem.}} &{} \\ \\
{\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\
{\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\
{\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\
{\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\
{\text{sentence that gives the information to find it.}} &{} \\
{\text{Translate into an equation}} &{d = 0.35(140)} \\ \\
{\textbf{Step 5. Solve} \text{ the equation.}} &{d = 49} \\ \\
{\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\
{ \text{Is a } $49 \text{ discount reasonable for a } $140 \text{ dress?} } &{} \\
{ \text{Yes.}} &{} \\\\ {\textbf{Step 7. Write} \text{ a complete sentence to answer}} &{\text{The amount of discount was }$49} \\ {\text{the question.}} &{}
\end{array}\)
(b) Read the problem again.
| Step 1. Identify what we are looking for. | the sale price of the dress |
| Step 2. Name what we are looking for. | |
| Choose a variable to represent that quantity. | Let s= the sale price. |
| Step 3. Translate into an equation. | |
| Write a sentence that gives the information to find it. |  |
| Translate into an equation. |  |
| Step 4. Solve the equation. |  |
| Step 5. Check. Does this make sense? | |
| Is the sale price less than the original price? | |
| Yes, $91 is less than $140. | |
| Step 6. Answer the question with a complete sentence. | The sale price of the dress was $91. |
Try It \(\PageIndex{35}\)
Find (a) the amount of discount and (b) the sale price:
Sergio bought a belt that was discounted 40% from an original price of $29.
- Answer
-
(a) $11.60, (b) $17.40
Try It \(\PageIndex{36}\)
Find (a) the amount of discount and (b) the sale price:
Oscar bought a barbecue that was discounted 65% from an original price of $395.
- Answer
-
(a) $256.75, (b) $138.25
There may be times when we know the original price and the sale price, and we want to know the discount rate. To find the discount rate, first we will find the amount of discount and then use it to compute the rate as a percent of the original price. Example \(\PageIndex{37}\) will show this case.
Example \(\PageIndex{37}\)
Jeannette bought a swimsuit at a sale price of $13.95. The original price of the swimsuit was $31. Find the (a) amount of discount and (b) discount rate.
Solution
\(\begin{array} {llll} { \text{(a)} } &{\text{Original price}} &{=} &{$31} \\
&{ \text{ Discount rate}} &{=} &{?} \\
&{ \text{ Discount}} &{=} &{$13.95} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{\text{The discount is the difference between the original}} \\ {} &{\text{price and the sale price.}} \\{\text{Translate into an equation}} &{d = 31 - 13.95} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 17.05} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is }17.05\text{ less than 31? Yes.}} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a complete sentence.}} &{\text{The amount of discount was }$17.05} \end{array}\)
(b) Read the problem again.
| Step 1. Identify what we are looking for. | the discount rate |
| Step 2. Name what we are looking for. | |
| Choose a variable to represent it. | Let \(r\) = the discount rate. |
| Step 3. Translate into an equation. | |
| Write a sentence that gives the information to find it. | 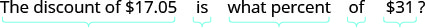 |
| Translate into an equation. | 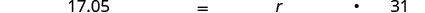 |
| Step 4. Solve the equation. | 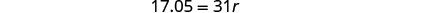 |
| Divide both sides by 31. | 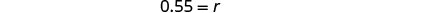 |
| Change to percent form. | 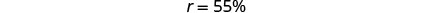 |
| Step 5. Check. Does this make sense? | |
| Is $17.05 equal to 55% of $31? | |
| \(17.05\stackrel{?}{=}0.55(31)\) | |
| \(17.05=17.05\checkmark\) | |
| Step 6. Answer the question with a complete sentence. | The rate of discount was 55%. |
Try It \(\PageIndex{38}\)
Find
- the amount of discount and
- the discount rate.
Lena bought a kitchen table at the sale price of $375.20. The original price of the table was $560.
- Answer
-
- $184.80
- 33%
Try It \(\PageIndex{39}\)
Find
- the amount of discount and
- the discount rate.
Nick bought a multi-room air conditioner at a sale price of $340. The original price of the air conditioner was $400.
- Answer
-
- $60
- 15%
Applications of mark-up are very common in retail settings. The price a retailer pays for an item is called the original cost. The retailer then adds a mark-up to the original cost to get the list price, the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.
We summarize the mark-up model in the box below.
MARK-UP
\[\begin{array}{l}{\text { amount of mark-up }=\text { mark-up rate } \times \text { original cost }} \\ {\text { list price }=\text { original cost }+\text { amount of mark up }}\end{array}\]
Keep in mind that the list price should always be more than the original cost.
Example \(\PageIndex{40}\)
Adam’s art gallery bought a photograph at original cost $250. Adam marked the price up 40%. Find the
- amount of mark-up and
- the list price of the photograph.
Solution
a.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the amount of mark-up |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let m = the amount of markup. |
| Step 4. Translate into an equation. | |
| Write a sentence that gives the information to find it. | 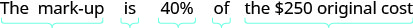 |
| Translate into an equation. |  |
| Step 5. Solve the equation. |  |
| Step 6. Check. Does this make sense? | |
| Yes, 40% is less than one-half and 100 is less than half of 250. | |
| Step 7. Answer the question with a complete sentence. | The mark-up on the photograph was $100. |
| Step 1. Read the problem again. | |
| Step 2. Identify what we are looking for. | the list price |
| Step 3. Name what we are looking for. | |
| Choose a variable to represent it. | Let p= the list price. |
| Step 4. Translate into an equation. | |
| Write a sentence that gives the information to find it. |  |
| Translate into an equation. | 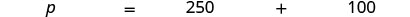 |
| Step 5. Solve the equation. |  |
| Step 6. Check. Does this make sense? | |
| Is the list price more than the net price? Is $350 more than $250? Yes. |
|
| Step 7. Answer the question with a complete sentence. | The list price of the photograph was $350. |
Try It \(\PageIndex{41}\)
Find
- the amount of mark-up and
- the list price.
Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.
- Answer
-
- $600
- $1,800
Try It \(\PageIndex{42}\)
Find
- the amount of mark-up and
- the list price.
The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.
- Answer
-
- $2,975
- $11,475
Key Concepts
- Percent Increase To find the percent increase:
- Find the amount of increase. increase=new amount−originalamount
- Find the percent increase. Increase is what percent of the original amount?
- Percent Decrease To find the percent decrease:
- Find the amount of decrease. decrease=original amount−newamount
- Find the percent decrease. Decrease is what percent of the original amount?
- Simple Interest If an amount of money, P, called the principal, is invested for a period of t years at an annual interest rate r, the amount of interest, I, earned is
\[\begin{array}{lllll} {} &{} &{I} &{=} &{\text { interest }}\\ {I = Prt} &{\text{where}} &{P} &{=} &{\text { principle }}\\ {} &{} &{r} &{=} &{\text { rate }}\\ {} &{} &{t} &{=} &{\text { time }} \end{array}\]
- Discount
- amount of discount is discount rate \( \times \) original price
- sale price is original price – discount
- Mark-up
- amount of mark-up is mark-up rate \( \times \) original cost
- list price is original cost + mark up
Glossary
- amount of discount
- The amount of discount is the amount resulting when a discount rate is multiplied by the original price of an item.
- discount rate
- The discount rate is the percent used to determine the amount of a discount, common in retail settings.
- interest
- Interest is the money that a bank pays its customers for keeping their money in the bank.
- list price
- The list price is the price a retailer sells an item for.
- mark-up
- A mark-up is a percentage of the original cost used to increase the price of an item.
- original cost
- The original cost in a retail setting, is the price that a retailer pays for an item.
- principal
- The principal is the original amount of money invested or borrowed for a period of time at a specific interest rate.
- rate of interest
- The rate of interest is a percent of the principal, usually expressed as a percent per year.
- simple interest
- Simple interest is the interest earned according to the formula I=Prt.


