2.6.6E: Exercises for Quadric Surfaces

Last updated

Jan 15, 2020
Save as PDF
- 2.6: Quadric Surfaces
- 2.7: Cylindrical and Spherical Coordinates

( \newcommand{\kernel}{\mathrm{null}\,}\)

For exercises 1 - 6, sketch and describe the cylindrical surface of the given equation.

1) [T] $𝑥 2 + 𝑧 2 = 1$

Answer

The surface is a cylinder with the rulings parallel to the $𝑦$ -axis.

$CNX_Calc_Figure_12_06_219.jfif$

2) [T] $𝑥 2 + 𝑦 2 = 9$

3) [T] $𝑧 = c o s (𝜋 2 + 𝑥)$

Answer

The surface is a cylinder with rulings parallel to the $𝑦$ -axis.

$CNX_Calc_Figure_12_06_202.jfif$

4) [T] $𝑧 = 𝑒 𝑥$

5) [T] $𝑧 = 9 - 𝑦 2$

Answer

The surface is a cylinder with rulings parallel to the $𝑥$ -axis.

$CNX_Calc_Figure_12_06_207.jfif$

6) [T] $𝑧 = l n 𝑥$

For exercises 7 - 10, the graph of a quadric surface is given.

a. Specify the name of the quadric surface.

b. Determine the axis of symmetry of the quadric surface.

$CNX_Calc_Figure_12_06_215.jfif$

Answer: a. Cylinder; b. The $𝑥$ -axis

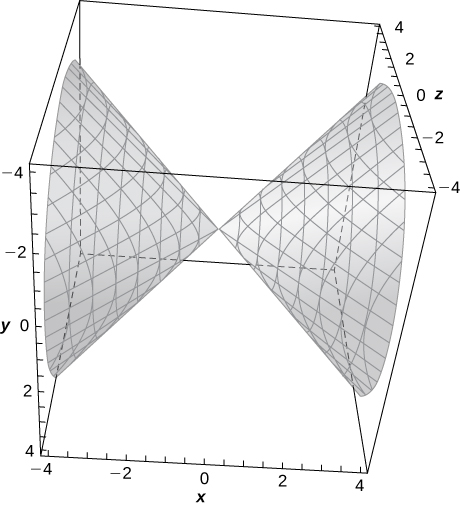
$CNX_Calc_Figure_12_06_214.jpg$

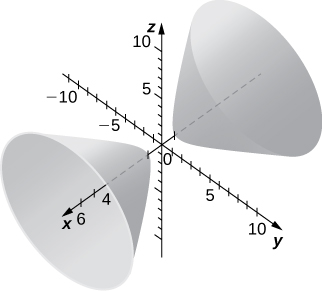
$CNX_Calc_Figure_12_06_221.jpg$

Answer: a. Hyperboloid of two sheets; b. The $𝑥$ -axis

10)

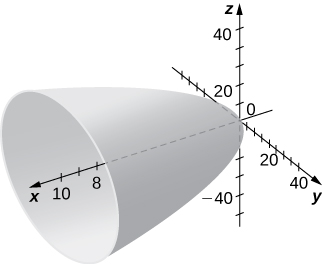
$CNX_Calc_Figure_12_06_222.jpg$

For exercises 11 - 16, match the given quadric surface with its corresponding equation in standard form.

a. $𝑥 2 4 + 𝑦 2 9 - 𝑧 2 12 = 1$

b. $𝑥 2 4 - 𝑦 2 9 - 𝑧 2 12 = 1$

c. $𝑥 2 4 + 𝑦 2 9 + 𝑧 2 12 = 1$

d. $𝑧 = 4 𝑥 2 + 3 𝑦 2$

e. $𝑧 = 4 𝑥 2 - 𝑦 2$

f. $4 𝑥 2 + 𝑦 2 - 𝑧 2 = 0$

11) Hyperboloid of two sheets

Answer: b.

12) Ellipsoid

13) Elliptic paraboloid

Answer: d.

14) Hyperbolic paraboloid

15) Hyperboloid of one sheet

Answer: a.

16) Elliptic cone

For exercises 17 - 28, rewrite the given equation of the quadric surface in standard form. Identify the surface.

17) $- 𝑥 2 + 36 𝑦 2 + 36 𝑧 2 = 9$

Answer: $- 𝑥 2 9 + 𝑦 2 14 + 𝑧 2 14 = 1,$ hyperboloid of one sheet with the $𝑥$ -axis as its axis of symmetry

18) $- 4 𝑥 2 + 25 𝑦 2 + 𝑧 2 = 100$

19) $- 3 𝑥 2 + 5 𝑦 2 - 𝑧 2 = 10$

Answer: $- 𝑥 2 103 + 𝑦 2 2 - 𝑧 2 10 = 1,$ hyperboloid of two sheets with the $𝑦$ -axis as its axis of symmetry

20) $3 𝑥 2 - 𝑦 2 - 6 𝑧 2 = 18$

21) $5 𝑦 = 𝑥 2 - 𝑧 2$

Answer: $𝑦 = - 𝑧 2 5 + 𝑥 2 5,$ hyperbolic paraboloid with the $𝑦$ -axis as its axis of symmetry

22) $8 𝑥 2 - 5 𝑦 2 - 10 𝑧 = 0$

23) $𝑥 2 + 5 𝑦 2 + 3 𝑧 2 - 15 = 0$

Answer: $𝑥 2 15 + 𝑦 2 3 + 𝑧 2 5 = 1,$ ellipsoid

24) $63 𝑥 2 + 7 𝑦 2 + 9 𝑧 2 - 63 = 0$

25) $𝑥 2 + 5 𝑦 2 - 8 𝑧 2 = 0$

Answer: $𝑥 2 40 + 𝑦 2 8 - 𝑧 2 5 = 0,$ elliptic cone with the $𝑧$ -axis as its axis of symmetry

26) $5 𝑥 2 - 4 𝑦 2 + 20 𝑧 2 = 0$

27) $6 𝑥 = 3 𝑦 2 + 2 𝑧 2$

Answer: $𝑥 = 𝑦 2 2 + 𝑧 2 3,$ elliptic paraboloid with the $𝑥$ -axis as its axis of symmetry

28) $49 𝑦 = 𝑥 2 + 7 𝑧 2$

For exercises 29 - 34, find the trace of the given quadric surface in the specified plane of coordinates and sketch it.

29) [T] $𝑥 2 + 𝑧 2 + 4 𝑦 = 0, 𝑧 = 0$

Answer

Parabola $𝑦 = - 𝑥 2 4,$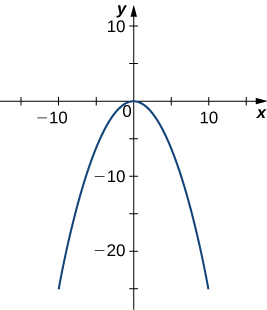

$CNX_Calc_Figure_12_06_223.jpg$

30) [T] $𝑥 2 + 𝑧 2 + 4 𝑦 = 0, 𝑥 = 0$

31) [T] $- 4 𝑥 2 + 25 𝑦 2 + 𝑧 2 = 100, 𝑥 = 0$

Answer

Ellipse $𝑦 2 4 + 𝑧 2 100 = 1,$

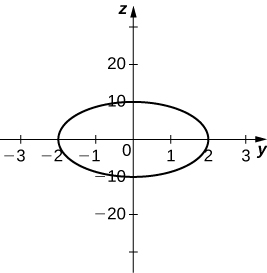
$CNX_Calc_Figure_12_06_206.jpg$

32) [T] $- 4 𝑥 2 + 25 𝑦 2 + 𝑧 2 = 100, 𝑦 = 0$

33) [T] $𝑥 2 + 𝑦 2 4 + 𝑧 2 100 = 1, 𝑥 = 0$

Answer

Ellipse $𝑦 2 4 + 𝑧 2 100 = 1,$

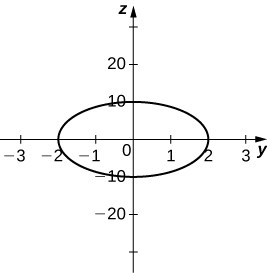
$CNX_Calc_Figure_12_06_209.jpg$

34) [T] $𝑥 2 - 𝑦 - 𝑧 2 = 1, 𝑦 = 0$

35) Use the graph of the given quadric surface to answer the questions.

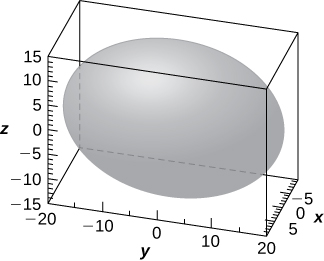
$CNX_Calc_Figure_12_06_226.jpg$

a. Specify the name of the quadric surface.

b. Which of the equations— $16 𝑥 2 + 9 𝑦 2 + 36 𝑧 2 = 3600, 9 𝑥 2 + 36 𝑦 2 + 16 𝑧 2 = 3600,$ or $36 𝑥 2 + 9 𝑦 2 + 16 𝑧 2 = 3600$ —corresponds to the graph?

c. Use b. to write the equation of the quadric surface in standard form.

Answer: a. Ellipsoid
b. The third equation
c. $𝑥 2 100 + 𝑦 2 400 + 𝑧 2 225 = 1$

36) Use the graph of the given quadric surface to answer the questions.

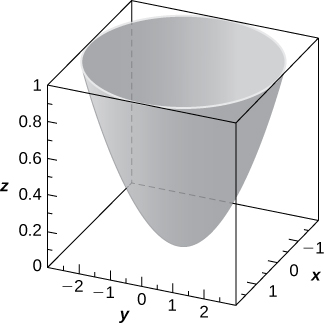
$CNX_Calc_Figure_12_06_227.jpg$

a. Specify the name of the quadric surface.

b. Which of the equations— $36 𝑧 = 9 𝑥 2 + 𝑦 2, 9 𝑥 2 + 4 𝑦 2 = 36 𝑧$ , or $- 36 𝑧 = - 81 𝑥 2 + 4 𝑦 2$ —corresponds to the graph above?

c. Use b. to write the equation of the quadric surface in standard form.

For exercises 37 - 42, the equation of a quadric surface is given.

a. Use the method of completing the square to write the equation in standard form.

b. Identify the surface.

37) $𝑥 2 + 2 𝑧 2 + 6 𝑥 - 8 𝑧 + 1 = 0$

Answer: a. $(𝑥 + 3) 2 16 + (𝑧 - 2) 2 8 = 1$
b. Cylinder centered at $(- 3, 2)$ with rulings parallel to the $𝑦$ -axis

38) $4 𝑥 2 - 𝑦 2 + 𝑧 2 - 8 𝑥 + 2 𝑦 + 2 𝑧 + 3 = 0$

39) $𝑥 2 + 4 𝑦 2 - 4 𝑧 2 - 6 𝑥 - 16 𝑦 - 16 𝑧 + 5 = 0$

Answer: a. $(𝑥 - 3) 2 4 + (𝑦 - 2) 2 - (𝑧 + 2) 2 = 1$
b. Hyperboloid of one sheet centered at $(3, 2, - 2),$ with the $𝑧$ -axis as its axis of symmetry

40) $𝑥 2 + 𝑧 2 - 4 𝑦 + 4 = 0$

41) $𝑥 2 + 𝑦 2 4 - 𝑧 2 3 + 6 𝑥 + 9 = 0$

Answer: a. $(𝑥 + 3) 2 + 𝑦 2 4 - 𝑧 2 3 = 0$
b. Elliptic cone centered at $(- 3, 0, 0),$ with the $𝑧$ -axis as its axis of symmetry

42) $𝑥 2 - 𝑦 2 + 𝑧 2 - 12 𝑧 + 2 𝑥 + 37 = 0$

43) Write the standard form of the equation of the ellipsoid centered at the origin that passes through points $𝐴 (2, 0, 0), 𝐵 (0, 0, 1),$ and $𝐶 (12, \sqrt 11, 12) .$

Answer: $𝑥 2 4 + 𝑦 2 16 + 𝑧 2 = 1$

44) Write the standard form of the equation of the ellipsoid centered at point $𝑃 (1, 1, 0)$ that passes through points $𝐴 (6, 1, 0), 𝐵 (4, 2, 0)$ and $𝐶 (1, 2, 1)$ .

45) Determine the intersection points of elliptic cone $𝑥 2 - 𝑦 2 - 𝑧 2 = 0$ with the line of symmetric equations $𝑥 - 1 2 = 𝑦 + 1 3 = 𝑧 .$

Answer: $(1, - 1, 0)$ and $(133, 4, 53)$

46) Determine the intersection points of parabolic hyperboloid $𝑧 = 3 𝑥 2 - 2 𝑦 2$ with the line of parametric equations $𝑥 = 3 𝑡, 𝑦 = 2 𝑡, 𝑧 = 19 𝑡$ , where $𝑡 \in 𝑅 .$

47) Find the equation of the quadric surface with points $𝑃 (𝑥, 𝑦, 𝑧)$ that are equidistant from point $𝑄 (0, - 1, 0)$ and plane of equation $𝑦 = 1 .$ Identify the surface.

Answer: $𝑥 2 + 𝑧 2 + 4 𝑦 = 0,$ elliptic paraboloid

48) Find the equation of the quadric surface with points $𝑃 (𝑥, 𝑦, 𝑧)$ that are equidistant from point $𝑄 (0, 2, 0)$ and plane of equation $𝑦 = - 2 .$ Identify the surface.

49) If the surface of a parabolic reflector is described by equation $400 𝑧 = 𝑥 2 + 𝑦 2,$ find the focal point of the reflector.

Answer: $(0, 0, 100)$

50) Consider the parabolic reflector described by equation $𝑧 = 20 𝑥 2 + 20 𝑦 2 .$ Find its focal point.

51) Show that quadric surface $𝑥 2 + 𝑦 2 + 𝑧 2 + 2 𝑥 𝑦 + 2 𝑥 𝑧 + 2 𝑦 𝑧 + 𝑥 + 𝑦 + 𝑧 = 0$ reduces to two parallel planes.

52) Show that quadric surface $𝑥 2 + 𝑦 2 + 𝑧 2 - 2 𝑥 𝑦 - 2 𝑥 𝑧 + 2 𝑦 𝑧 - 1 = 0$ reduces to two parallel planes passing.

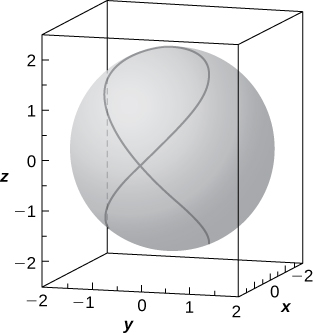
53) [T] The intersection between cylinder $(𝑥 - 1) 2 + 𝑦 2 = 1$ and sphere $𝑥 2 + 𝑦 2 + 𝑧 2 = 4$ is called a Viviani curve.

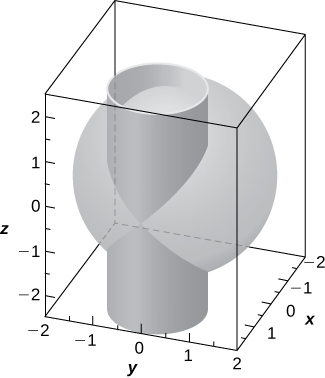
$CNX_Calc_Figure_12_06_228.jpg$

a. Solve the system consisting of the equations of the surfaces to find the equation of the intersection curve. (Hint: Find $𝑥$ and $𝑦$ in terms of $𝑧$ .)

b. Use a computer algebra system (CAS) or CalcPlot3D to visualize the intersection curve on sphere $𝑥 2 + 𝑦 2 + 𝑧 2 = 4$ .

Answer

a. $𝑥 = 2 - 𝑧 2 2, 𝑦 = \pm 𝑧 2 \sqrt 4 - 𝑧 2,$ where $𝑧 \in [- 2, 2];$

$CNX_Calc_Figure_12_06_229.jpg$

54) Hyperboloid of one sheet $25 𝑥 2 + 25 𝑦 2 - 𝑧 2 = 25$ and elliptic cone $- 25 𝑥 2 + 75 𝑦 2 + 𝑧 2 = 0$ are represented in the following figure along with their intersection curves. Identify the intersection curves and find their equations (Hint: Find y from the system consisting of the equations of the surfaces.)

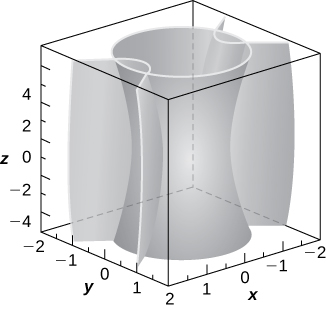
$CNX_Calc_Figure_12_06_230.jpg$

55) [T] Use a CAS or CalcPlot3D to create the intersection between cylinder $9 𝑥 2 + 4 𝑦 2 = 18$ and ellipsoid $36 𝑥 2 + 16 𝑦 2 + 9 𝑧 2 = 144$ , and find the equations of the intersection curves.

Answer

two ellipses of equations $𝑥 2 2 + 𝑦 2 92 = 1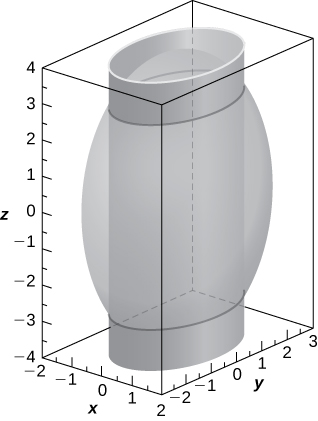$ in planes $𝑧 = \pm 2 \sqrt 2$

$CNX_Calc_Figure_12_06_231.jpg$

56) [T] A spheroid is an ellipsoid with two equal semiaxes. For instance, the equation of a spheroid with the z-axis as its axis of symmetry is given by $𝑥 2 𝑎 2 + 𝑦 2 𝑎 2 + 𝑧 2 𝑐 2 = 1$ , where $𝑎$ and $𝑐$ are positive real numbers. The spheroid is called oblate if $𝑐 < 𝑎$ , and prolate for $𝑐 > 𝑎$ .

a. The eye cornea is approximated as a prolate spheroid with an axis that is the eye, where $𝑎 = 8.7 𝑚 𝑚$ and $𝑐 = 9.6 𝑚 𝑚$ .Write the equation of the spheroid that models the cornea and sketch the surface.

b. Give two examples of objects with prolate spheroid shapes.

57) [T] In cartography, Earth is approximated by an oblate spheroid rather than a sphere. The radii at the equator and poles are approximately $3963$ mi and $3950$ mi, respectively.

a. Write the equation in standard form of the ellipsoid that represents the shape of Earth. Assume the center of Earth is at the origin and that the trace formed by plane $𝑧 = 0$ corresponds to the equator.

b. Sketch the graph.

c. Find the equation of the intersection curve of the surface with plane $𝑧 = 1000$ that is parallel to the $𝑥 𝑦$ -plane. The intersection curve is called a parallel.

d. Find the equation of the intersection curve of the surface with plane $𝑥 + 𝑦 = 0$ that passes through the $𝑧$ -axis. The intersection curve is called a meridian.

Answer

a. $𝑥 2 39632 + 𝑦 2 39632 + 𝑧 2 39502 = 1$

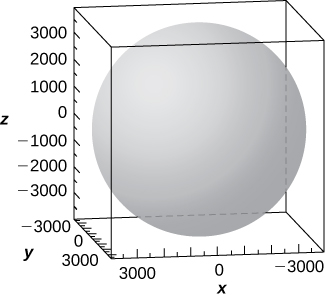
$CNX_Calc_Figure_12_06_233.jpg$

c. The intersection curve is the ellipse of equation $𝑥 2 39632 + 𝑦 2 39632 = (2950) (4950) 39502$ , and the intersection is an ellipse.
d. The intersection curve is the ellipse of equation $2 𝑦 2 39632 + 𝑧 2 39502 = 1 .$

58) [T] A set of buzzing stunt magnets (or “rattlesnake eggs”) includes two sparkling, polished, superstrong spheroid-shaped magnets well-known for children’s entertainment. Each magnet is $1.625$ in. long and $0.5$ in. wide at the middle. While tossing them into the air, they create a buzzing sound as they attract each other.

a. Write the equation of the prolate spheroid centered at the origin that describes the shape of one of the magnets.

b. Write the equations of the prolate spheroids that model the shape of the buzzing stunt magnets. Use a CAS or CalcPlot3D to create the graphs.

59) [T] A heart-shaped surface is given by equation $(𝑥 2 + 94 𝑦 2 + 𝑧 2 - 1) 3 - 𝑥 2 𝑧 3 - 980 𝑦 2 𝑧 3 = 0 .$

a. Use a CAS or CalcPlot3D to graph the surface that models this shape.

b. Determine and sketch the trace of the heart-shaped surface on the $𝑥 𝑧$ -plane.

Answer

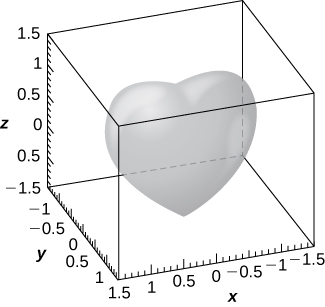
$CNX_Calc_Figure_12_06_237.jpg$

b. The intersection curve is $(𝑥 2 + 𝑧 2 - 1) 3 - 𝑥 2 𝑧 3 = 0 .$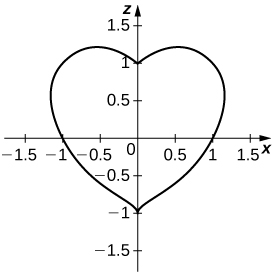

$CNX_Calc_Figure_12_06_238.jpg$

60) [T] The ring torus symmetric about the $𝑧$ -axis is a special type of surface in topology and its equation is given by $(𝑥 2 + 𝑦 2 + 𝑧 2 + 𝑅 2 - 𝑟 2) 2 = 4 𝑅 2 (𝑥 2 + 𝑦 2)$ , where $𝑅 > 𝑟 > 0$ . The numbers $𝑅$ and $𝑟$ are called are the major and minor radii, respectively, of the surface. The following figure shows a ring torus for which $𝑅 = 2$ and $𝑟 = 1$ .

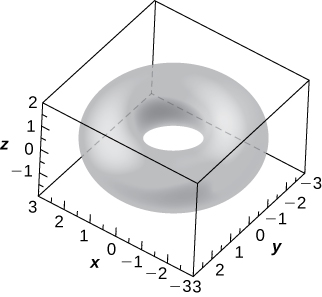
$CNX_Calc_Figure_12_06_239.jpg$

a. Write the equation of the ring torus with $𝑅 = 2$ and $𝑟 = 1$ , and use a CAS or CalcPlot3D to graph the surface. Compare the graph with the figure given.

b. Determine the equation and sketch the trace of the ring torus from a. on the $𝑥 𝑦$ -plane.

c. Give two examples of objects with ring torus shapes.

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors

Contributors

Support Center

How can we help?