2.1: Systems of Equations

Back when studying linear equations, we found the intersection of two lines.  Doing so allowed us to solve interesting problems by finding a pair of values that satisfied two different equations.  While we did not call it this at the time, we were solving a system of equations.  To start out, we will review an example of the type of problem we've solved before.

Example $\PageIndex{1}$

A small business produces soap and lotion gift baskets.  Labor, utilities, and other fixed expenses cost $6,000 a month.  Each basket costs $8 to produce, and sells for $20.  How many baskets does the company need to sell each month to break even?

Solution

In business terms, "break even" means for revenue (money brought in) to equal costs.  While this problem can be approached in several ways, we will approach here by first creating two linear functions, one for the costs, and another for revenue.

 

Let's define $n$ to be the number of gift baskets the company sells in a month.  There are $6,000 of fixed costs each month, and costs increase by $8 for each basket, so we can write the linear function for costs, $C$, as:

$$C(n) = 6000 + 8n \nonumber$$

Each sale brings in $20, so the revenue, $R$, after selling $n$ baskets will be:

 $$R(n) = 20n \nonumber$$

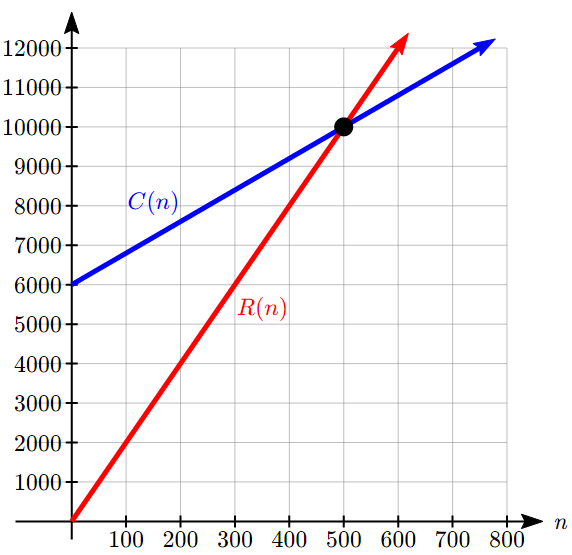To find the break-even point, we are looking for the number of baskets where the revenue will equal the costs.  In other words, if we were to graph the two linear functions, we are looking for the point that lies on both lines; the solution is the point that satisfies both equations.

In this case we could probably solve the problem from the graph itself, but we can also solve it algebraically by setting the equations equal:

$$\begin{array}{rclll} R(n) &=& C(n) && \\ 20n &=& 6000 + 8n && \text{Subtract } 8n \text{ from both sides} \\ 12n &=& 6000 && \text{Divide} \\ n &=& \frac{6000}{12} = 500 && \text{Evaluate either function at this input} \\ R(500) &=& C(500) = 10,000 && \end{array} \nonumber$$

The break even point is at 500 baskets.  The company must sell 500 baskets a month, at which point their revenue of $10,000 will cover their total costs of $10,000.

The example above illustrates one type of system of equations, one where both equations are given in functional form.  When the equations are written this way, it is easy to solve the system using substitution, by setting the two outputs equal, and solving for the input.  However, many system of equations problems are not written this way.

Example $\PageIndex{2}$

A company produces a basic and premium version of its product.  The basic version requires 20 minutes of assembly and 15 minutes of painting.  The premium version requires 30 minutes of assembly and 30 minutes of painting.  If the company has staffing for 3,900 minutes of assembly and 3,300 minutes of painting each week.  If the company wants to fully utilize all staffed hours, how many of each item should they produce?

Solution

Notice first that this problem has two variables, or two unknowns - the number of basic products to make, and the number of premium products to make.  There are also two constraints - the hours of assembly and the hours of painting available.  This is going to give us two equations in two unknowns, what we call a 2 by 2 system of equations.

We will start by defining our variables:

$b$: the number of basic products produced

$p$: the number of premium products produced

Now we can create our equations based on the constraints.  Each basic product requires 20 minutes of assembly, so producing $b$ items will require 20$b$ minutes.   Each premium product requires 30 minutes of assembly, so producing $p$ items will require 30$p$ minutes. Together we have 3,900 minutes available, giving us the equation:

$$20b + 30p = 3900 \nonumber$$

Using the same approach for painting gives the equation

$$15b + 30p = 3300 \nonumber$$

Together, these form our system of equations.  They are sometimes written as a pair with a curly bracket on the left to indicate that they should be considered as connected equations. 

$$\left\{ \begin{gathered} 20b + 30p = 3900 \\ 15b + 30p = 3300 \end{gathered} \right. \nonumber$$

As before, our goal is to find a pair of values, $b, p$, that satisfies both equations.  We will return to this problem and solve it shortly.

While it may not be clear, the equation $20b + 30p = 3900$ we constructed above is a linear equation, like the linear equations from the first example, it is just written differently. We could, if desired, solve this equation for $p$ to get it written in slope-intercept form:

$$30p = 3900 - 20b, \quad \text{so} \quad p = 130 - \frac{2}{3}b \nonumber$$

We typically do not do this, since it often makes the system harder to solve then when using other techniques.  To dive into this further, let's first clarify what it means to find a solution to a system of linear equations.

Definition: System of Linear Equations

A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously.

A solution to a system is a set of numerical values for each variable in the system that will satisfy all equations in the system at the same time.

Not every system will have exactly one solution, but we'll look more closely at that later.  To check to see if an ordered pair is a solution to a system of equations, you would:

1. Substitute the ordered pair into each equation in the system.
2. Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.

Example $\PageIndex{3}$

Determine whether the ordered pair $(5,1)$ is a solution to the given system of equations.

Solution

$$\left\{ \begin{gathered} x + 3y = 8 \hfill \\ 2x - 9 = y \hfill \\ \end{gathered} \right. \nonumber$$

Substitute the ordered pair $(5,1)$ into both equations.

$$\begin{align*} (5) + 3(1) &= 8 & \\ 8 &= 8 & {\text{True}} \\ 2(5) - 9 &= (1)&\\ 1 &= 1 & {\text{True}} \\ \end{align*} \nonumber$$

The ordered pair $(5,1)$ satisfies both equations, so it is the solution to the system.

There are three common methods for solving systems of linear equations with two variables.  The first is solving by graphing.  In the first example above we graphed both equations, and the solution to the system was the intersection of the lines. 

Example $\PageIndex{4}$

Solve the following system of equations by graphing.

$$\begin{gathered} 2x + y = - 8 \\ x - y = - 1 \\ \end{gathered} \nonumber$$

Solution

Solve the first equation for $y.$

$$\begin{align*} 2x + y &= - 8 \\ y &= - 2x - 8 \\ \end{align*} \nonumber$$

Solve the second equation for $y.$

$$\begin{align*} x - y &= - 1 \\ y &= x + 1 \\ \end{align*} \nonumber$$

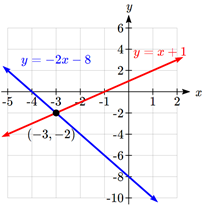Graph both equations on the same set of axes. The lines appear to intersect at the point $(- 3, - 2)$. We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations.

$$\begin{align*} 2( - 3) + ( - 2) &= - 8& \\ - 8 &= - 8 & \text{True} \\ ( - 3) - ( - 2) &= - 1 & \\ - 1 &= - 1 & \text{True} \\ \end{align*} \nonumber$$

The solution to the system is the ordered pair $(- 3, - 2)$.

 

Exercise $\PageIndex{1}$

Solve the following system of equations by graphing.

$$\begin{align*} 2x - 5y & = - 25 \\ - 4x + 5y &= 35 \\ \end{align*} \nonumber$$

Answer

The solution to the system is the ordered pair $( - 5,3)$.

While this method can work well enough when the solution values are both integers, it is not very useful when the intersection is not at a clear point.  Additionally, it requires solving both equations for $y$, which adds extra steps.  Because of these limitations, solving by graphing is rarely used, but can be useful for checking whether your algebraic answers are reasonable.

Solving a System by Substitution

Another method for solving a system of equations is the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable.

Solving a system using substitution

1. Solve one of the two equations for one of the variables in terms of the other.
2. Substitute the expression for this variable into the second equation, then solve for the remaining variable.
3. Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
4. Check the solution in both equations.

The problem we did in Example 1 was technically done by substitution, but it was made easier since both equations were already solved for one variable, $y$.  An example of a more typical case is shown next.

Example $\PageIndex{5}$

Solve the following system of equations by substitution.

$$\begin{align*} - x + y &= - 5 \\ 2x - 5y &= 1 \\ \end{align*} \nonumber$$

Solution

First, we will solve the first equation for $y$.

$$\begin{align*} - x + y &= - 5 \\ y &= x - 5 \\ \end{align*} \nonumber$$

Now we can substitute the expression $x - 5$ for $y$ in the second equation.

$$\begin{align*} 2x - y &= - 5y \\ 2x-5(x-5) &=1 \\ 2x-5x+25 &=1\\ -3x &= -24 \\ x &=8 \end{align*} \nonumber$$

Now, we substitute $x = 8$ into the first equation and solve for $y.$

$$\begin{align*} - (8) + y &= - 5 \\ y &= 3 \\ \end{align*} \nonumber$$

Our solution is $(8,3)$.

We can check the solution by substituting $(8,3)$ into both equations.

$$\begin{align*} - x + y &= - 5 & \\ -(8) + (3) &= -5 & \text{True} \\ 2x-5 &= 1 &\\ 2(8)-5(3) &= 1 & \text{True} \end{align*} \nonumber$$

Exercise $\PageIndex{2}$

 Solve the following system of equations by substitution.

$$\begin{align*} x &= y + 3 \\ 4 &= 3x - 2y \\ \end{align*} \nonumber$$

Answer

$(-2, -5)$

Substitution can always be used, but is an especially good choice when one of the variables in one of the equations has a coefficient of 1 or -1, making it easy to solve for that variable without introducing fractions.  This is fairly common in many applications.

Example $\PageIndex{6}$

Julia has just retired, and has $600,000 in her retirement account that she needs to reallocate to produce income.  She is looking at two investments:  a very safe guaranteed annuity that will provide 3% interest, and a somewhat riskier bond fund that averages 7% interest.  She would like to invest as little as possible in the riskier bond fund, but needs to produce $40,000 a year in interest to live on.  How much should she invest in each account?

Solution

Notice there are two unknowns in this problem: the amount she should invest in the annuity and the amount she should invest in the bond fund.  We can start by defining variables for the unknowns:

$a$: The amount (in dollars) she invests in the annuity

$b$: The amount (in dollars) she invests in the bond fund.

Our first equation comes from noting that together she is going to invest $600,000:

$$a + b = 600,000 \nonumber$$

Our second equation will come from the interest.  She earns 3% on the annuity, so the interest earned in a year would be $0.03a$.  Likewise, the interest earned on the bond fund in a year would be $0.07b$.  Together, these need to total $40,000, giving the equation:

$$0.03a + 0.07b = 40,000 \nonumber$$

Together, these two equations form our system.  The first equation is an ideal candidate for the first step of substitution - we can easily solve the equation for $a$ or $b$:

$$a = 600,000 - b \nonumber$$

Then we can substitute this expression for a in the second equation and solve.

$$\begin{align*} 0.03(600,000 - b) + 0.07b &= 30,000 \\ 18,000 - 0.03b + 0.07b &= 40,000 \\ 0.04b &= 22,000 \\ b &= 550,000 \end{align*} \nonumber$$

Now substitute this back into the equation $a = 600,000 - b$ to find $a$

$$\begin{align*} a &= 600,000 - 550,000 \\ a &= 50,000 \\ \end{align*} \nonumber$$

In order to reach her goal, Julia will have to invest $550,000 in the bond fund, and $50,000 in the annuity.

Solving a System by the Addition Method

A third method of solving systems of linear equations is the addition method, also called the elimination method.  In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero.  Of course, not all systems are set up with the two terms of one variable having opposite coefficients.  Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.

Solving a System by the Addition Method 

1. Write both equations with $x$ and $y$-variables on the left side of the equal sign and constants on the right.
2. Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
3. Solve the resulting equation for the remaining variable.
4. Substitute that value into one of the original equations and solve for the second variable.
5. Check the solution by substituting the values into the other equation.

Often using the addition method will require multiplying one or both equations by a constant so terms will eliminate.  Using these approaches, we can revisit the equation from Example 2.

Example $\PageIndex{7}$

In Example 2, we set up the system below. Solve it.

$$\left\{ {\begin{array}{c} {20b + 30p = 3900} \\ {15b + 30p = 3300} \end{array}} \right. \nonumber$$

Solution

Adding the equations would not eliminate a variable, but we notice that the coefficients on $p$ are the same, so multiplying one of the equations by $-1$ will change the sign of the coefficients.  Multiplying the second equation by $-1$ gives the system

$$\begin{array}{c} {20b + 30p = 3900} \\ { - 15b - 30p = - 3300} \end{array} \nonumber$$

Adding these equations gives

$$\begin{gathered} 5b = 600 \hfill \\ b = 120 \hfill \\ \end{gathered} \nonumber$$

Substituting $b = 30$ into the first equation,

$$\begin{align*} 20(120) + 30p &= 3900 \\ 2400 + 30p &= 3900 \\ 30p &= 1500 \\ p &= 50 \\ \end{align*} \nonumber$$

The solution is $b = 120, p = 50$, meaning the company should produce 120 basic products and 50 premium products to full utilize staffed hours.

Checking our answer in the second equation:

$$\begin{align*} 15(120) + 30(50) &= 3300 \\ 1800 + 1500 &= 3300 \\ 3300 &= 3300 \\ \end{align*} \nonumber$$

Exercise $\PageIndex{3}$

Solve the system of equations by addition.

$$\begin{align*} 2x - 7y &= 2 \\ 3x + y &= - 20 \\ \end{align*} \nonumber$$

Answer

$(-6, -2)$

Example $\PageIndex{8}$

Solve the given system of equations in two variables by addition.

$$\begin{align*} 2x + 3y &= -16 \\ 5x - 10y &= 30 \end{align*}$$

Solution

One equation has $2x$ and the other has $5x.$ The least common multiple is $10x$  so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate $x$ by multiplying the first equation by $- 5$ and the second equation by $2$.

$$\begin{align*} -5(2x + 3y) &= - 5(- 16) \\ - 10x - 15y &= 80 \\ 2(5x - 10y) &= 2(30) \\ 10x - 20y &= 60 \\ \end{align*} \nonumber$$

Then, we add the two equations together.

$$\begin{align*} - 10x - 15y &= 80 \\ 10x - 20y &= 60 \\ \hline - 35y &= 140 \\ y &= - 4 \\ \end{align*} \nonumber$$

Substitute $y = - 4$ into the original first equation.

$$\begin{align*} 2x + 3( - 4) &= - 16 \\ 2x - 12 &= - 16 \\ 2x &= - 4 \\ x &= - 2 \\ \end{align*} \nonumber$$

The solution is $( - 2, - 4 )$. Check it in the other equation.

$$\begin{align*} 5x - 10y &= 30 \\ 5(- 2) - 10(- 4)&= 30 \\ -10 + 40 &= 30 \\ 30 &= 30 \\ \end{align*} \nonumber$$

Exercise $\PageIndex{4}$

Solve the system of equations by addition.

$$\begin{align*} 2x + 3y &= 8 \\ 3x + 5y &= 10 \\ \end{align*}$$

Answer

$(10, -4)$

Dependent and Inconsistent Systems

Up until now, we have only considered cases where there is exactly one solution to the system.  We can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution, such as the examples we just explored. The two lines have different slopes and intersect at one point in the plane.

A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.

Another type of system of linear equations is an inconsistent system, which is one in which the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.

Types of Linear Systems

• An independent system has exactly one solution pair $(x,y)$. The point where the two lines intersect is the only solution.
• An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
• A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.

  Independent System

  Inconsistent System

  Dependent System

We can use substitution or addition to identify inconsistent systems. Recall that an inconsistent system consists of parallel lines that have the same slope but different y-intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement, such as $12 = 0$.

Example $\PageIndex{9}$

Solve the following system of equations.

$$\begin{align*} x &= 9 - 2y \\ x + 2y &= 13 \end{align*}$$

Solution

We can approach this problem in two ways. Because one equation is already solved for $x,$ the most obvious step is to use substitution.

$$\begin{align*} x + 2y &= 13 \\ (9 - 2y) + 2y &= 13 \\ 9 + 0y &= 13 \\ 9 &= 13 \\ \end{align*} \nonumber$$

Clearly, this statement is a contradiction (a false statement) because $9 \ne 13$. Therefore, the system has no solution, and the system is inconsistent.

Recall that a dependent system of equations in two variables is a system in which the two equations represent the same line. Dependent systems have an infinite number of solutions because all of the points on one line are also on the other line. After using substitution or addition, the resulting equation will be an identity, such as $0 = 0.$

Example $\PageIndex{10}$

Find a solution to the system of equations using the addition method.

$$\begin{align*} x + 3y &= 2 \\ 3x + 9y &= 6 \end{align*} \nonumber$$

Solution

With the addition method, we want to eliminate one of the variables by adding the equations. In this case, let’s focus on eliminating $x.$ If we multiply both sides of the first equation by $- 3$, then we will be able to eliminate the $x$-variable.

$$x + 3y = 2$$

Multiply both sides of the equation by - 3,

$$\begin{align*} (- 3)(x + 3y) &= (- 3)(2) \\ - 3x - 9y &= - 6 \\ \end{align*} \nonumber$$

$$\begin{align*} - 3x - 9y &= - 6 \\ 3x + 9y &= 6 \\ \hline 0 &= 0 \hfill \\ \end{align*} \nonumber$$

We can see that there will be an infinite number of solutions that satisfy both equations.  In some cases, realizing there are an infinite number of solutions is enough, and we can stop there.  In other cases, we will want to describe the set of solutions. 

One way is to simply say it's the set of points that satisfy $x + 3y = 2$, but often we would solve that equation for $y$ and describe the solution as set of points $\left( x, - \frac{1}{3}x + \frac{2}{3} \right)$.

Exercise $\PageIndex{5}$

Solve the systems:

a.  $$\begin{align*} 2y - 2x &= 2 \\ 2y - 2x &= 6 \end{align*}$$

b. $$\begin{align*} y - 2x &= 5 \\ - 3y + 6x &= - 15 \end{align*}$$

Answer

a. No solution.  The system is inconsistent.

b. The system is dependent so there are infinite solutions of the form $(x,2x + 5).$

Systems with 3 variables in 3 unknowns

In systems of two variables, a solution was an ordered pair $(x, y)$ that satisfied both equations.  The solution set to a three-by-three system is an ordered triple $(x,y,z)$. Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room.  A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.

Example $\PageIndex{11}$

Determine whether the ordered triple $(3, - 2,1)$ is a solution to the system.

$$\begin{align*} x + y + z &= 2 \\ 6x - 4y + 5z &= 31 \\ 5x + 2y + 2z &= 13 \\ \end{align*}$$

Solution

We will check each equation by substituting in the values of the ordered triple for $x,$ $y,$ and $z.$

$$\begin{align*} x + y + z &= 2 \\ (3) + (-2) + (1) &= 2 \\ \text{True}& \\ \end{align*}$$

$$\begin{align*} 6x - 4y + 5z &= 31 \\ 6 (3) - 4(-2) + 5(1) &= 31 \\ 18 + 8 + 5 &= 31 \\ \text{True}& \\ \end{align*}$$

$$\begin{align*} 5x + 2y + 2z &= 13 \\ 5(3) + 2(-2) + 2(1) &= 13 \\ 15 - 4 + 2 &= 13 \\ \text{True}& \\ \end{align*}$$

The ordered triple $( 3, - 2,1)$  is indeed a solution to the system.

We can utilize the techniques we learned in the last section to solve $3\times 3$ systems of equations by reducing the problem to one we already know how to solve.

Given a linear system of three equations, solve for three unkowns

1. Pick any pair of equations and solve for one variable.

2. Pick another pair of equations and solve for the same variable.

3. You have created a system of two equations in two unknowns.  Solve the resulting two-by-two system. 

4. Back-substitute known variables into any one of the original equations and solve for the missing variable.

Example $\PageIndex{12}$

Find a solution to the following system.  The equations are numbered so we can refer to them more easily.

$$\begin{align*} x - 2y + 3z &= 9 & (1) \\ - x + 3y - z &= - 6 &(2) \\ 2x - 5y + 5z &= 17 &(3) \\ \end{align*} \nonumber$$

Solution

There will always be several choices as to where to begin, but the most obvious first step here is to eliminate $x$ by adding equations (1) and (2).

$$\begin{align*} x - 2y + 3z &= 9 &(1) \\ - x + 3y - z &= - 6 &(2) \\ \hline y + 2z &= 3 &(4) \\ \end{align*} \nonumber$$

The second step is multiplying equation (1) by $- 2$ and adding the result to equation (3). These two steps will eliminate the variable $x.$

$$\begin{align*} - 2x + 4y - 6z &= - 18 & (1) \text{ multiplied by -2} \\ 2x - 5y + 5z &= 17 &(3) \\ \hline - y - z &= - 1 &(5) \hfill \\ \end{align*} \nonumber$$

In equations (4) and (5), we have created a new two-by-two system. We can solve for $z$ by adding the two equations.

$$\begin{align*} y + 2z &= 3 &(4) \\ - y - z &= - 1 &(5) \\ \hline z &= 2 &(6) \\ \end{align*} \nonumber$$

Choosing one equation from each new system, we obtain the upper triangular form:

$$\begin{align*} x - 2y + 3z &= 9 &(1) \\ y + 2z &= 3 &(4) \\ z &= 2 &(6) \\ \end{align*} \nonumber$$

Next, we back-substitute  $z = 2$ into equation (4) and solve for $y$.

$$\begin{align*} y + 2(2) &= 3 \\ y + 4 &= 3 \\ y &= -1 \\ \end{align*} \nonumber$$

Finally, we can back-substitute $z = 2$ and $y = - 1$ into equation (1). This will yield the solution for $x$.

$$\begin{align*} x - 2(- 1) + 3(2) &= 9 \\ x + 2 + 6 &= 9 \\ x &= 1 \\ \end{align*} \nonumber$$

The solution is the ordered triple $(1, - 1,2)$.

Exercise $\PageIndex{6}$

Solve the system of equations in three variables.

$$\begin{align*} 2x + y - 2z &= - 1 \\ 3x - 3y - z &= 5 \\ x - 2y + 3z &= 6 \\ \end{align*} \nonumber$$

Answer

$(1, -1, 1)$

Many problems in real life depend on more than two unknowns.

Example $\PageIndex{13}$

Chad is trying to plan a meal to meet specific nutritional goals.  He wants to construct a dish containing rice, tofu, and peanuts that will provide 30g of protein, 14g of fat, and 50g of carbohydrates.  How much of each ingredient should he use?

Solution

First off, we're assuming any other ingredients used in the recipe aren't contributing significantly enough to the nutrition to be considered.  To answer this question, we'll first need to know the nutritional content for the ingredients.  Looking these up:

White rice:  1 cup provides:  0g fat, 44g carbohydrates, 4g protein

Tofu:          1 cup provides:  10g fat, 5g carbohydrates, 20g protein

Peanuts:     1 cup provides:  72g fat, 31g carbohydrates, 35g protein

 

Now we can define our variables.  We are interested in the amount of each ingredient to use, so we'll define our variables as the quantity of each ingredient:

$r$:  cups of rice, $t$: cups of tofu, $p$: cups of peanuts.

Now for each nutrient, we can create an equation.  Since 1 cup of rice provides 44g carbohydrates, $r$ cups will provide $44r$ grams of carbohydrates.  Likewise t cups of tofu will provide $5t$ grams, and $p$ cups of peanuts will provide $31p$ grams.  Together we want our recipe to provide 50g of carbohydrates, giving the equation:

$$44r + 5t + 31p = 50 \nonumber$$

Doing the same for fat and protein gives the full system:

$$\begin{align*} 44r + 5t + 31p &= 50 \\ 10t + 72p &= 14 \\ 4r + 20t + 35p &= 30 \\ \end{align*} \nonumber$$

Now we can solve the system.

Step 1. Notice that the section equation already does not involve the variable $r$.  to make things simpler, a first step might be to interchange the last two equations so the two equations with three variables will line up.

$$\begin{align*} 44r + 5t + 31p &= 50 &(1) \\ 4r + 20t + 35p &= 30 &(2) \\ 10t + 72p &= 14 &(3) \\ \end{align*}$$

Step 2.  Since $r$ is already eliminated in the last equation, we will eliminate $r$ from the first two equations.  Multiply equation (2) by -11.

$$\begin{align*} 44r + 5t + 31p &= 50 &(1) \\ - 44r - 220t - 385p &= -330 &(2) \\ 10t + 72p &= 14 &(3) \\ \end{align*} \nonumber$$

Step 3.  Add equations (1) and (2), writing the result as row 2.

$$\begin{align*} 44r + 5t + 31p &= 50 &(1) \\ - 215t - 384p &= -280 &(2) \\ 10t + 72p &= 14 &(3) \\ \end{align*}$$

Step 4.  Multiply equation (2) by 2 and equation (3) by 43

$$\begin{align*} 44r + 5t + 31p &= 50 &(1) \\ -430t - 708p &= -560 &(2) \\ 430t + 3096p &= 602 &(3) \\ \end{align*}$$

Step 5.  Add equations (2) and (3), writing the result in row 3

$$\begin{align*} 44r + 5t + 31p &= 50 &(1) \\ - 430t - 708p &= - 560 &(2) \\ 2388p &= 42 &(3) \\ \end{align*} \nonumber$$

Step 6.  Solve for $p$ in equation 3.  For a real life problem like this, decimal approximations are probably fine.

$$\begin{align*} 2388p &= 42 \\ p &= \frac{42}{2388} \approx 0.0176 \\ \end{align*} \nonumber$$

Step 7.  Back substitute the value for $p$ into equation (2) to solve for $t$.

$$\begin{align*} - 430t - 708(0.0176) &= - 560 \\ - 430t - 12.4608 &= - 560 \\ - 430t &= - 547.5392 \\ t &= \frac{- 547.5392}{-430} \approx 1.273 \\ \end{align*} \nonumber$$

Step 8.  Back substitute the values for $p$ and $t$ and into equation (1) and solve for $r$.

$$\begin{align*} 44r + 5(1.273) + 31(0.0176) &= 50 \\ 44r &= 43.0894 \\ r & \approx 0.979 \\ \end{align*}$$

To meet his nutritional goals, Chad should use 0.979 cups of rice, 1.273 cups of tofu, and 0.0176 cups of peanuts.

This particular system was rather unpleasant to solve.  In the rest of the chapter we will learn some other techniques for solving complex systems.

Important Topics of this Section

Solving systems

   Graphing

   Elimination

   Addition

Setting up systems of equations

Inconsistent and dependent systems

Solving 3 by 3 systems