1.4: Definition of Limit

Last updated
Save as PDF

Page ID: 212008

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

It may seem strange that we have been using and calculating the values of limits for quite a while without having a precise definition of “limit,” but the history of mathematics shows that many concepts — including limits — were successfully used before they were precisely defined or even fully understood. We have chosen to follow the historical sequence, emphasizing the intuitive and graphical meaning of limit because most students find these ideas and calculations easier than the definition. (This intuitive and graphical understanding of limit was sufficient for the first 100-plus years of the development of calculus — from Newton and Leibniz in the late 1600s to Cauchy in the early 1800s — and it is sufficient for using and understanding the results in beginning calculus.}

Mathematics, however, is more than a collection of useful tools, and part of its power and beauty comes from the fact that in mathematics terms are precisely defined and results are rigorously proved. Mathematical tastes (what is mathematically beautiful, interesting, useful) change over time, but because of careful definitions and proofs, the results remain true — everywhere and forever. Textbooks seldom give all of the definitions and proofs, but it is important to mathematics that such definitions and proofs exist.

The goal of this section is to provide a precise definition of the limit of a function. The definition will not help you calculate the values of limits, but it provides a precise statement of what a limit is. The definition of limit is then used to verify the limits of some functions and prove some general results.

The Intuitive Approach

The precise (“formal”) definition of limit carefully states the ideas that we have already been using graphically and intuitively. The following side-by-side columns show some of the phrases we have been using to describe limits, and those phrases — particularly the last ones — provide the basis on which to build the definition of limit.

A Particular Limit	General Limit
$\displaystyle\lim_{x\to 3} \, 2x - 1 = 5$	$\displaystyle\lim_{x\to a} \, f(x) = L$
“as the values of $x$ approach $3$, the values of $2x-1$ approach (are arbitrarily close to) $5$”	“as the values of $x$ approach $a$, the values of $f(x)$ approach (are arbitrarily close to) $L$”
“when $x$ is close to $3$ (but not equal to $3$), the value of $2x-1$ is close to $5$”	“when $x$ is close to $a$ (but not equal to $a$), the value of $f(x)$ is close to $L$”
“we can guarantee that the values of $2x-1$ are as close to $5$ as we want by restricting the values of $x$ to be sufficiently close to $3$ (but not equal to $3$)”	“we can guarantee that the values of $f(x)$ are as close to $L$ as we want by restricting the values of $x$ to be sufficiently close to $a$(but not equal to $a$)”

Let’s examine what the last phrase (“we can …”) means for the Particular Limit in the previous discussion.

Example $\PageIndex{1}$

We know $\displaystyle\lim_{x\to 3} \, 2x - 1 = 5$ and need to show that we can guarantee that the values of $f(x) = 2x - 1$ are as close to $5$ as we want by restricting the values of $x$ to be sufficiently close to $3$. What values of $x$ guarantee that $f(x) = 2x - 1$ is within:

$1$ unit of $5$?
$0.2$ units of $5$?
$E$ units of $5$?

Solution

“Within $1$ unit of $5$” means between $5-1 = 4$ and $5+1 = 6$, so the question can be rephrased as “for what values of $x$ is $y = 2x - 1$ between $4$ and $6$: $4 < 2x - 1 < 6$?” We want to know which values of $x$ ensure the values of $y = 2x -1$ are in the the shaded band:
$A first-quadrant graph showing a solid blue straight line f(x) = 2x-1. A wide horizontal yellow band stretches across the graph between y = 4 and y = 6, labeled 'y is within 1 of 5' and the spans between 4 and 5, and 5 and 6, denoted by double-sided arrows of length 1.$
The algebraic process is straightforward:\[4 < 2x - 1 < 6 \quad \Rightarrow \quad 5 < 2x < 7 \quad \Rightarrow \quad 2.5 < x < 3.5\nonumber\]We can restate this result as follows: “If $x$ is within $0.5$ units of $3$, then $y = 2x-1$ is within $1$ unit of $5$.”
$The same image as the previous figure, but with a vertical orange band stretching from x = 2.5 to x = 3.5, labeled 'x is withing 0.5 of 3.'$
Any smaller distance also satisfies the guarantee: for example, “If $x$ is within $0.4$ units of $3$, then $y = 2x-1$ is within $1$ unit of $5$.”
$The same image as in the previous figure but with a second, narrower, vertical band centered at x = 3 and labeled 'x is within 0.4 of 3.'$
“Within $0.2$ units of $5$” means between $5-0.2 = 4.8$ and $5+0.2 = 5.2$, so the question can be rephrased as “for which values of $x$ is $y = 2x - 1$ between $4.8$ and $5.2$: $4.8 < 2x - 1 < 5.2$?” Solving for $x$, we get $5.8 < 2x < 6.2$ and $2.9 < x < 3.1$. “If $x$ is within $0.1$ units of $3$, then $y = 2x-1$ is within $0.2$ units of $5$.”
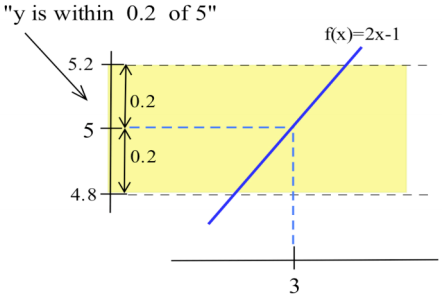
$A graph of a blue line f(x) = 2x-1 near the point (3,5) with a horizontal yellow band extending from y=4.8 to y=5.2, labeled 'y is within 0.2 of 5'; the vertical spans from 4.8 to 5 and 5 to 5.2 are denoted by vertical double arrows labeled 0.2.$
Any smaller distance also satisfies the guarantee.

Rather than redoing these calculations for every possible distance from $5$, we can do the work once, generally:

“Within $E$ unit of $5$” means between $5-E$ and $5+E$, so the question becomes, “For what values of $x$ is $y = 2x - 1$ between $5-E$ and $5+E$: $5-E < 2x - 1 < 5+E$?” Solving $5-E < 2x - 1 < 5+E$ for $x$, we get:\[6-E < 2x < 6+E \quad \Rightarrow \quad 3 - \frac{E}{2} < x < 3 + \frac{E}{2}\nonumber\]“If $x$ is within $\frac{E}{2}$ units of $3$, then $y = 2x-1$ is within $E$ units of $5$.”
$The same image as in the previous figure, but with a vertical orange band extending from x=2.9 to x=3.1 labeled 'x is within 0.1 of 3.'$
Any smaller distance also works.

Part (c) of Example 1 illustrates the power of general solutions in mathematics. Rather than redoing similar calculations every time someone demands that $f(x) = 2x - 1$ be within some given distance of $5$, we did the calculations once. And then we can quickly respond for any given distance. For the question “What values of $x$ guarantee that $f(x) = 2x - 1$ is within $0.4$, $0.1$ or $0.006$ units of $5$?” we can answer, “If $x$ is within $0.2$ (\)= \frac{0.4}{2}\)), $0.05$ (\)=\frac{0.1}{2}\)) or $0.003$ ($=\frac{0.006}{2}$) units of $3$.”

Practice $\PageIndex{1}$

Knowing that $\displaystyle\lim_{x\to 2} \, 4x - 5 = 3$, determine which values of $x$ guarantee that $f(x) = 4x - 5$ is within

$1$ unit of $3$.
$0.08$ units of $3$.
$E$ units of $3$.

$A graph of a blue line f(x) = 4x-5 near the point (2,3) with a horizontal yellow band extending from y=3-E to y=3+E, labeled 'y is within E of 3'; the vertical spans from 3-E to 3 and 3 to 3+E are denoted by vertical double arrows labeled E.$

Answer

$3 - 1 < 4x - 5 < 3 + 1 \Rightarrow 7 < 4x < 9 \Rightarrow 1.75 < x < 2.25$:\\ “$x$ within $\frac14$ unit of $2$.”
$3 - 0.08 < 4x - 5 < 3 + 0.08 \Rightarrow 7.92 < 4x < 8.08 \Rightarrow 1.98 < x < 2.02$: “$x$ within $0.02$ units of $2$.”
$3 - E < 4x - 5 < 3 + E \Rightarrow 8 - E < 4x < 8 + E \Rightarrow 2 - \frac{E}{4} < x < 2 + \frac{E}{4}$: “$x$ within $\frac{E}{4}$ units of $2$.”

The same ideas work even if the graphs of the functions are not straight lines, but the calculations become more complicated.

Example $\PageIndex{2}$

Knowing that $\displaystyle\lim_{x\to 2} \, x^2 = 4$, determine which values of $x$ guaranteethat $f(x) = x^2$ is within:

$1$ unit of $4$.
$0.2$ units of $4$.

State each answer in the form: “If $x$ is within units of $2$, then $f(x)$ is within units of $4$.”

$A graph of a blue curve f(x) = x^2 near the point (2,4) with a horizontal yellow band extending from y=3 to y=5, labeled 'y is within 1 of 4'; the vertical spans from 3 to 4 and 4 to 5 are denoted by vertical double arrows labeled 1.$

Solution

If $x^2$ is within $1$ unit of $4$ (and $x$ is near $2$, hence positive) then $3 < x^2 < 5$ so $\sqrt{3} < x < \sqrt{5}$ or $1.732 < x < 2.236$. The interval containing these $x$ values extends from $2 - \sqrt{3} \approx 0.268$ units to the left of $2$ to $\sqrt{5} - 2 \approx 0.236$ units to the right of $2$.
$The same image as in the previous figure, but with a vertical orange band extending from x = 1.724 to x = 2.236 labeled 'x is withing 0.236 of 3.'$
Because we want to specify a single distance on each side of $2$, we can pick the {\em smaller} of the two distances, $0.236$, and say: “If $x$ is within $0.236$ units of $2$, then $f(x)$ is within $1$ unit of $4$.”
Similarly, if $x^2$ is within $0.2$ units of $4$ (and $x$ is near $2$, so $x>0$) then $3.8 < x^2 < 4.2$ so $\sqrt{3.8} < x < \sqrt{4.2}$ or $1.949 < x < 2.049$. The interval containing these $x$ values extends from $2 - \sqrt{3.8} \approx 0.051$ units to the left of $2$ to $\sqrt{4.2} - 2 \approx 0.049$ units to the right of $2$. Again picking the smaller of the two distances, we can say: “If $x$ is within $0.049$ units of $2$, then $f(x)$ is within $1$ unit of $4$.”

The situation in Example $\PageIndex{2}$ — with different distances on the left and right sides — is very common, and we always pick our single distance to be the smaller of the distances to the left and right. By using the smaller distance, we can be certain that if $x$ is within that smaller distance on either side, then the value of $f(x)$ is within the specified distance of the value of the limit.

Practice $\PageIndex{2}$

Knowing that $\displaystyle\lim_{x\to 9} \sqrt{x} = 3$, determine which values of $x$ guarantee that $f(x) = \sqrt{x}$ is within:

$1$ unit of $3$.
$0.2$ units of $3$.

State each answer in the form: “If $x$ is within units of $9$, then $f(x)$ is within units of $3$.”

$A graph of a blue curve f(x) = sqrt(x) near the point (9,3) with a horizontal yellow band extending from y=2 to y=4, labeled 'y is within 1 of 3'; the vertical spans from 2 to 3 and 3 to 4 are denoted by vertical double arrows labeled 1.$

Answer

“Within $1$ unit of $3$”: If $2 < \sqrt{x} < 4$, then $4 < x < 16$, which extends from $5$ units to the left of $9$ to $7$ units to right of $9$. Using the smaller of these two distances from $9$: “If $x$ is within $5$ units of $9$, then $\sqrt{x}$ is within $1$ unit of $3$.”
“Within $0.2$ units of $3$”: If $2.8 < \sqrt{x} < 3.2$, then $7.84 < x < 10.24$, which extends from $1.16$ units to the left of $9$ to $1.24$ units to the right of $9$. “If $x$ is within $1.16$ units of $9$, then $x$ is within $0.2$ units of $3$.

The same ideas can also be used when the function and the specified distance are given graphically, and in that case we can give the answer graphically.

Example $\PageIndex{3}$

In the figure below, $\displaystyle\lim_{x\to 2} \, f(x) = 3$:

$A graph of a blue curve f(x) near the point (2,3) that consists of a line segment with negative slope to the left of x = 3 and a steeper line segment with positive slope to the right of x = 3. A vertical distance is denoted E.$

Which values of $x$ guarantee that $y = f(x)$ is within $E$ units (given graphically) of $3$? State your answer in the form: “If $x$ is within ({\em show a distance $D$ graphically}) of $2$, then $f(x)$ is within $E$ units of $3$.”

Solution

The solution process requires several steps:

Use the given distance $E$ to find the values $3 - E$ and $3 + E$ on the $y$-axis:
$The same image as in the previous figure, but with a horizontal yellow band extendning from y = 3-E to y = 3+E and two intervals on the horizontal axis, labeled D_L and D_R, that correspond to the inputs to the left and right of x = 2, respectively, that yield values of f(x) in the yellow band.$
Sketch the horizontal band with lower edge at $y = 3 - E$ and upper edge at $y = 3 + E$.
Find the first locations to the right and left of $x = 2$ where the graph of $y = f(x)$ crosses the lines $y = 3 - E$ and $y = 3 + E$, and at these locations draw vertical line segments extending to the $x$-axis.
On the $x$-axis, graphically determine the distance from $2$ to the vertical line on the left (labeled $D_L$) and from $2$ to the vertical line on the right (labeled $D_R$).
Let the length $D$ be the smaller of the lengths $D_L$ and $D_R$.
$The same image as in the previous figure, but with a vertical orange band extending from x = 2-D to x = 2+D, where D is the same as D_R in the previous image.$

If $x$ is within $D$ units of $2$, then $f(x)$ is within $E$ units of $3$.

Practice $\PageIndex{3}$

In figure below, $\displaystyle\lim_{x\to 3} f(x) = 1.8$. Which values of $x$ guarantee that $y = f(x)$ is within $E$ units (given graphically) of $1.8$?

$A graph of a red curve f(x) near the point (3,1.8) that consists of a line segment with positive slope to the left of x = 3 and a less steep line segment with negative slope to the right of x = 3. A vertical distance is denoted E. An open dot appears at (3,1.8) and closed dot appears a distance (greather than E) above the open dot.$

Answer: $A graph of a red curve f(x) near the point (3,1.8) that consists of a line segment with positive slope to the left of x = 3 and a less steep line segment with negative slope to the right of x = 3. A vertical distance is denoted E. An open dot appears at (3,1.8) and closed dot appears a distance (greather than E) above the open dot. A horizontal yellow band extends from y = 1.8-E to y=1.8+E with the distances from 1.8-E to 1.8 and 1.8 to 1.8+E indicated as E. A vertical orange band is centered at x=3. The distance from x= to the left edge of the orange band is indicated as D_L and a greater distance from x= to a point beyond the orange band is indicated as D_R. A caption reads: D = smaller of D_L and D_R = {a double arrow the same length as D_L}.$

The Formal Definition of Limit

The ideas from the previous Examples and Practice problems, restated for general functions and limits, provide the basis for the definition of limit given below. The use of the lowercase Greek letters $\epsilon$ (epsilon) and $\delta$ (delta) in the definition is standard, and this definition is sometimes called the “epsilon-delta” definition of a limit.

Definition of $\displaystyle\lim_{x\to a} f(x) = L$

For every given number $\epsilon > 0$ there is a number $\delta > 0$ so that:

if: $x$ is within $\delta$ units of $a$ (and $x \neq a$)

then: $f(x)$ is within $\epsilon$ units of $L$

Equivalently: $\left|f(x)-L\right|<\epsilon$ whenever $0<\left|x-a\right|<\delta$

In this definition, $\epsilon$ represents the given distance on either side of the limiting value $y = L$, and $\delta$ is the distance on each side of the point $x = a$ on the $x$-axis that we have been finding in the previous examples. This definition has the form of a “challenge and response”: for any positive challenge $\epsilon$ (make $f(x)$ within $\epsilon$ of $L$), there is a positive response $\delta$ (start with $x$ within $\delta$ of $a$ and $x \neq a$).

$A graph of a blue curve y = f(x) centered at (a,L) with a horizontal yellow band extending from L-epsilon to L+epsilon labeled 'y is within epsilon of L' and a vertical orange band extending from a-delta to a+delta labeled 'x is within delta of a.'$

Example $\PageIndex{4}$

As seen in the figure below, $\displaystyle\lim_{x\to a} f(x) = L$, with a value for $\epsilon$ given graphically as a length:

$A graph of a blue curve y = f(x) centered at (a,L) with an open dot at (a,L), a closed dot below that open dot, and a vertical distance labeled epsilon.$

Find a length for $\delta$ that satisfies the definition of limit (so “if $x$ is within $\delta$ of $a$, and $x \neq a$, then $f(x)$ is within $\epsilon$ of $L$”).

Solution

Follow the steps outlined in Example $\PageIndex{3}$. The length for $\delta$ is shown here:

$A graph of a blue curve y = f(x) centered at (a,L) with an open dot at (a,L), a closed dot below that open dot, and a vertical distance labeled epsilon. A horizontal yellow band extends from L-epsilon to L+epsilon and a vertical orange band extends from a-delta to a+delta, labeled 'x is within delta of a.'$

and any shorter length for $\delta$ also satisfies the definition.

Practice $\PageIndex{4}$

In figure below, $\displaystyle\lim_{x\to a} f(x) = L$, with a value for $\epsilon$ given graphically:

$A graph of a blue curve y = f(x) centered at (a,L) with an open dot at (a,L), a closed dot above that open dot, and a vertical distance labeled epsilon.$

Find a length for $\delta$ that satisfies the definition of limit.

Answer: $A graph of a blue curve y = f(x) centered at (a,L) with an open dot at (a,L), a closed dot above that open dot, and a vertical distance labeled epsilon. A horizontal yellow band extends from L-epsilon to L+epsilon, labeled 'y is within epsilon of L,' and a vertical orange band extends from a-delta to a+delta, labeled 'x is within delta of a.'$

Example $\PageIndex{5}$

Prove that $\displaystyle\lim_{x\to 3} \, 4x - 5 = 7$.

Solution

We need to show that “for every given $\epsilon > 0$ there is a $\delta > 0$ so that if $x$ is within $\delta$ units of $3$ (and $x \neq 3$) then $4x - 5$ is within $\epsilon$ units of $7$.”

Actually, there are two things we need to do. First, we need to find a value for $\delta$ (typically depending on $\epsilon$) and, second, we need to show that our $\delta$ really does satisfy the “if … then … ” part of the definition.

Finding $\delta$ is similar to part (c) in Example 1 and Practice 1: Assume $4x - 5$ is within $\epsilon$ units of $7$ and solve for $x$. If $7 - \epsilon < 4x - 5 < 7 + \epsilon$ then $12 - \epsilon < 4x < 12 + \epsilon \Rightarrow 3 - \frac{\epsilon}{4} < x < 3 + \frac{\epsilon}{4}$ so $x$ is within $\frac{\epsilon}{4}$ units of $3$. Put $\delta = \frac{\epsilon}{4}$.

To show that $\delta = \frac{\epsilon}{4}$ satisfies the definition, we merely reverse the order of the steps in the previous paragraph. Assume that $x$ is within $\delta$ units of $3$. Then $3 - \delta < x < 3 + \delta$, so: \begin{align*}3 - \frac{\epsilon}{4} < x < 3 + \frac{\epsilon}{4} \quad &\Rightarrow \quad 12 - \epsilon < 4x < 12 + \epsilon\\ &\Rightarrow \quad 7 - \epsilon < 4x - 5 < 7 + \epsilon\end{align*} so we can conclude that $f(x) = 4x - 5$ is within $\epsilon$ units of $7$. This formally verifies that $\displaystyle\lim_{x\to 3} \, 4x - 5 = 7$.

Practice $\PageIndex{5}$

Prove that $\displaystyle\lim_{x\to 4} \, 5x + 3 = 23$.

Answer

Given any $\epsilon > 0$, take $\delta = \frac{\epsilon}{5}$. If $x$ is within $\delta = \frac{\epsilon}{5}$ of $4$, then $4 - \frac{\epsilon}{5} < x < 4 + \frac{\epsilon}{5}$ so:\[- \frac{\epsilon}{5} < x - 4 < \frac{\epsilon}{5} \Rightarrow -\epsilon < 5x - 20 < \epsilon \Rightarrow -\epsilon < (5x + 3) - 23 < \epsilon\nonumber\]so, finally, $f(x) = 5x + 3$ is within $\epsilon$ of $L = 23$.

We have shown that “for any $\epsilon > 0$, there is a $\delta > 0$ (namely $\delta = \frac{\epsilon}{5}$)” so that the rest of the definition is satisfied.

The method used to prove the values of the limits for these particular linear functions can also be used to prove the following general result about the limits of linear functions.

Theorem

$\displaystyle\lim_{x\to a} \, mx+b = ma+b$

Proof

Let $f(x) = mx + b$.

Case 1: $m = 0$. Then $f(x) = 0x + b = b$ is simply a constant function, and any value for $\delta > 0$ satisfies
the definition. Given any value of $\epsilon > 0$, let $\delta = 1$ (any positive value for $\delta$ works). If $x$ is
is within $1$ unit of $a$, then $f(x) - f(a) = b - b = 0 < \epsilon$, so we have shown that for any $\epsilon > 0$ there is a $\delta > 0$ that satisfies the limit definition.

Case 2: $m \neq 0$. For any $\epsilon > 0$, put $\delta = \frac{\epsilon}{\left|m\right|} > 0$. If $x$ is within $\delta = \frac{\epsilon}{\left|m\right|}$ of $a$ then\[a - \frac{\epsilon}{\left|m\right|} < x < a + \frac{\epsilon}{\left|m\right|} \Rightarrow \frac{\epsilon}{\left|m\right|} < x - a < \frac{\epsilon}{\left|m\right|}
\Rightarrow \left| x - a \right| < \frac{\epsilon}{\left|m\right|}\nonumber\]
Then the distance between $f(x)$ and $L = ma + b$ is:
\begin{align*}\left| f(x) - L \right| &= \left| (mx + b) - (ma + b) \right| = \left|mx-ma\right|\\
&= \left|m\right| \cdot \left| x - a \right| < \left|m\right| \frac{\epsilon}{\left|m\right|} = \epsilon
\end{align*}
so $f(x)$ is within $\epsilon$ of $L = ma + b$.

$A graph of a blue line y = mx+b centered at (a,L), where L=ma+b, with a horizontal yellow band extending from L-epsilon to L+epsilon, and a vertical orange band extending from a-delta to a+delta. A vertical distance is denoted epsilon and a caption reads delta = epsilon/m.$

In each case, we have shown that “given any $\epsilon > 0$, there is a $\delta > 0$” that satisfies the rest of the limit definition.

If there is even a single value of $\epsilon$ for which there is no $\delta$, then we say that the limit “{\bf does not exist}.”

Example $\PageIndex{6}$

With $f(x)$ defined as:$f(x) = \left\{
\begin{array}{rl}
{ 2 } & { \text{if } x < 1 } \\
{ 4 } & { \text{if } x > 1 } \end{array}\right.$use the limit definition to prove that $\displaystyle\lim_{x\to 1} f(x)$ does not exist.

$A graph of a blue piecewise graph with f(x) = 2 for x<1, f(x) = 4 for x>1, and open dots at (1,2) and (1,4).$

Solution

One common proof technique in mathematics is called “proof by contradiction” and that is the method we use here:

We assume that the limit does exist and equals some number $L$.
We show that this assumption leads to a contradiction
We conclude that the assumption must have been false.

We therefore conclude that the limit does not exist.

First, assume that the limit exists: $\displaystyle\lim_{x\to 1} f(x) = L$ for some value for $L$. Let $\epsilon = \frac12$. Then, because we are assuming that the limit exists, there is a $\delta > 0$ so that if $x$ is within $\delta$ of $1$ then $f(x)$ is within $\epsilon$ of $L$. (The definition says “for every $\epsilon$” so we can certainly pick $\frac12$ as our $\epsilon$ value; why we chose this particular value for $\epsilon$ shows up later in the proof.)

Next, let $x_1$ be between $1$ and $1 + \delta$. Then $x_1 > 1$ so $f(x_1) = 4$. Also, $x_1$ is within $\delta$ of $1$ so $f(x_1) = 4$ is within $\frac12$ of $L$, which means that $L$ is between $3.5$ and $4.5$: $3.5 < L < 4.5$.

Let $x_2$ be between $1$ and $1 - \delta$. Then $x_2 < 1$, so $f(x_2) = 2$. Also, $x_2$ is within $\delta$ of $1$ so $f(x_2) = 2$ is within $\frac12$ of $L$, which means that $L$ is between $1.5$ and $2.5$: $1.5 < L < 2.5$.

These inequalities provide the contradiction we hoped to find. There is no value $L$ that satisfies both $3.5 < L < 4.5$ {\bf and} $1.5 < L < 2.5$, so our assumption must be false: $f(x)$ does not have a limit as $x \rightarrow 1$.

Practice $\PageIndex{6}$

Use the limit definition to prove that $\displaystyle\lim_{x\to 0} \, \frac{1}{x}$ does not exist.

$A graph of y = 1/x.$

Answer

Using “proof by contradiction” as in the solution to Example $\PageIndex{6}$ (this is a much more sophisticated [= harder] problem):

Assume that the limit exists: $\displaystyle\lim_{x\to 0} \, \frac{1}{x} = L$ for some value of $L$. Let $\epsilon = 1$. Since we’re assuming that the limit exists, there is a $\delta > 0$ so that if $x$ is within $\delta$ of $0$ then $f(x) = \frac{1}{x}$ is within $\epsilon = 1$ of $L$. (The definition says “for every $\epsilon$” so we can pick $\epsilon = 1$. For this particular limit, the definition fails for every $\epsilon > 0$.) FIGURE
Let $x_1$ be between $0$ and $0 + \delta$ and also require that $x_1 < \frac12$. Then $0 < x_1 < \frac12$ so $f(x_1) = \frac{1}{x_1} > 2$. Because $x_1$ is within $\delta$ of $0$, $f(x_1) > 2$ is within $\epsilon = 1$ of $L$, so $L > 2 - \epsilon = 1$: that is, $1 < L$. Let $x_2$ be between $0$ and $0 - \delta$ and also require $x_2 > -\frac12$. Then $0 > x_2 > \frac12$ so $f(x_2) = \frac{1}{x_2} < -2$. Since $x_2$ is within $\delta$ of $0$, $f(x_2) < -2$ is within $\epsilon = 1$ of $L$, so $L < -2 + \epsilon = -1 \Rightarrow -1 > L$.
The two inequalities derived above provide the contradiction we were hoping to find. There is no value $L$ that satisfies {\bf both} $1 < L$ and $L < -1$, so we can conclude that our assumption was false and that $f(x) = \frac{1}{x}$ does not have a limit as $x \rightarrow 0$.

Proofs of Two Limit Theorems

We conclude with proofs of two parts of the Main Limit Theorem so you can see how such proofs proceed — you have already used these theorems to evaluate limits. (There are rigorous proofs of all of the other limit properties in the Main Limit Theorem, but they are somewhat more complicated than the proofs given here.)

Theorem

If: $\displaystyle\lim_{x\to a} \, f(x) = L$

then: $\displaystyle\lim_{x\to a} \, k\cdot f(x) = kL$

Proof

Case $k = 0$: The theorem is true but not very interesting:\[\lim_{x\to a} k\cdot f(x) = \lim_{x\to a} 0\cdot f(x) = \lim_{x\to a} 0 = 0 = 0\cdot L = kL\nonumber\]

Case $k \neq 0$: Because $\displaystyle\lim_{x\to a} f(x) = L$, then, by the definition, for every $\epsilon > 0$ there is a $\delta > 0$ so that $\left| f(x) - L \right| < \epsilon$ whenever $\left| x - a \right| < \delta$. For any $\epsilon > 0$, we know $\frac{\epsilon}{\left|k\right|} > 0$, so pick a value of $\delta$ that satisfies $\left| f(x) - L \right| < \frac{\epsilon}{\left|k\right|}$ whenever $\left| x - a \right| < \delta$.

When $\left| x - a \right| < \delta$ (“\)x\) is within $\delta$ of $a$”) then $\left| f(x) - L \right| < \frac{\epsilon}{\left|k\right|}$ (“\)f(x)\) is within $\frac{\epsilon}{\left|k\right|}$ of $L$”) so $\left|k\right|\cdot \left| f(x) - L \right| < \epsilon \quad \Rightarrow \quad \left| k\cdot f(x) - k\cdot L \right| < \epsilon$ (that is, $k\cdot f(x)$ is within $\epsilon$ of $k\cdot L$).

Theorem

If: $\displaystyle\lim_{x\to a} \, f(x) = L$ \quad and \quad $\displaystyle\lim_{x\to a} g(x) = M$

then: $\displaystyle\lim_{x\to a} \, \left[f(x) + g(x)\right] = L+M$.

Proof

Given any $\epsilon > 0$, we know $\frac{\epsilon}{2} > 0$, so there is a number $\delta_{f} > 0$ such that when $\left| x - a \right| < \delta_{f}$ then $\left| f(x) - L \right| < \frac{\epsilon}{2}$ (“if $x$ is within $\delta_{f}$ of $a$, then $f(x)$ is within $\frac{\epsilon}{2}$ of $L$”).

Likewise, there is a number $\delta_{g} > 0$ such that when $\left| x - a \right| < \delta_{g}$ then $\left| g(x) - M \right| < \frac{\epsilon}{2}$ (“if $x$ is within $\delta_{g}$ of $a$, then $g(x)$ is within $\frac{\epsilon}{2}$ of $M$”).

Let $\delta$ be the smaller of $\delta_{f}$ and $\delta_{g}$. If $\left| x - a \right| < \delta$ then $\left| f(x) - L \right| < \frac{\epsilon}{2}$ and $\left| g(x) - M \right| < \frac{\epsilon}{2}$ so:
\begin{align*}
\left| (f(x) + g(x)) - (L + M)) \right| &= \left| (f(x) - L) + (g(x) - M) \right| \\
&\leq \left| f(x) - L \right| + \left| g(x) - M \right| < \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon %\qquad &(\mbox{rearranging the terms})\\ %&(\mbox{using the Triangle Inequality})\\
\end{align*}
so $f(x)+g(x)$ is within $\epsilon$ of $L+M$ whenever $x$ is within $\delta$ of $a$.

Problems

In Problems 1--4, state each answer in the form “If $x$ is within units of … ”

Knowing that $\displaystyle\lim_{x\to 3} \, 2x + 1 = 7$, what values of $x$ guarantee that $f(x) = 2x + 1$ is within:
1. $1$ unit of $7$?
2. $0.6$ units of $7$?
3. $0.04$ units of $7$?
4. $\epsilon$ units of $7$?
Knowing that $\displaystyle\lim_{x\to 1} \, 3x + 2 = 5$, what values of $x$ guarantee that $f(x) = 3x + 2$ is within:
1. $1$ unit of $5$?
2. $0.6$ units of $5$?
3. $0.09$ units of $5$?
4. $\epsilon$ units of $5$?
Knowing that $\displaystyle\lim_{x\to 2} \, 4x - 3 = 5$, what values of $x$ guarantee that $f(x) = 4x - 3$ is within:
1. $1$ unit of $5$?
2. $0.4$ units of $5$?
3. $0.08$ units of $5$?
4. $\epsilon$ units of $5$?
Knowing that $\displaystyle\lim_{x\to 1} \, 5x - 3 = 2$, what values of $x$ guarantee that $f(x) = 5x - 3$ is within:
1. $1$ unit of $2$?
2. $0.5$ units of $2$?
3. $0.01$ units of $2$?
4. $\epsilon$ units of $2$?
For Problems 1--4, list the slope of each function $f$ and the $\delta$ (as a function of $\epsilon$). For these linear functions $f$, how is $\delta$ related to the slope?
You have been asked to cut two boards (exactly the same length after the cut) and place them end to end. If the combined length must be within $0.06$ inches of $30$ inches, then each board must be within how many inches of $15$?
You have been asked to cut three boards (exactly the same length after the cut) and place them end to end. If the combined length must be within $0.06$ inches of $30$ inches, then each board must be within how many inches of $10$?
Knowing that $\displaystyle\lim_{x\to 3} \, x^2 = 9$, what values of $x$ guarantee that $f(x) = x^2$ is within:
1. $1$ unit of $9$?
2. $0.2$ units of $9$?
Knowing that $\displaystyle\lim_{x\to 2} \, x^3 = 8$, what values of $x$ guarantee that $f(x) = x^3$ is within:
1. $0.5$ units of $8$?
2. $0.05$ units of $8$?
Knowing that $\displaystyle\lim_{x\to 16} \, \sqrt{x} = 4$, what values of $x$ guarantee that $f(x) = \sqrt{x}$ is within:
1. $1$ unit of $4$?
2. $0.1$ units of $4$?
Knowing that $\displaystyle\lim_{x\to 3} \, \sqrt{1+x} = 2$, what values of $x$ guarantee that $f(x) = \sqrt{1+x}$ is within:
1. $1$ unit of $2$?
2. $0.0002$ units of $2$?
You must cut four pieces of wire (all the same length) and form them into a square. If the area of the square must be within $0.06$ in\)^2\) of $100$ in\)^2\), then each piece of wire must be within how many inches of $10$ in?
You need to cut four pieces of wire (all the same length) and form them into a square. If the area of the square must be within $0.06$ in\)^2\) of $25$ in\)^2\), then each piece of wire must be within how many inches of $5$ in?

Problems 14–17 give $\displaystyle\lim_{x\to a} \, f(x) = L$, the function $f$ and a value for $\epsilon$ graphically. Find a length for $\delta$ that satisfies the limit definition for the given function and value of $\epsilon$.

$A blue curve y = f(x) passing through (a,L) with a vertical distance epsilon indicated.$
$A blue curve y = f(x) passing through (a,L) with an open dot at that point and a vertical distance epsilon indicated.$
$A blue curve y = f(x) passing through (a,L) with an open dot at that point and closed dot above that point, as well as a vertical distance epsilon indicated. The graph to the left of x = a is concave up and the graph to the right is a line segment with negative slope.$
$A blue curve y = f(x) passing through (a,L) with an open dot at that point and closed dot above that point, as well as a vertical distance epsilon indicated. To the right of x =a the graph changes from an increasing smooth graph to a decreasing linear graph.$
Redo each of Problems 14--17 taking a new value of $\epsilon$ to be half the value of $\epsilon$ given in the problem.

In Problems 19–22, use the limit definition to prove that the given limit does not exist. (Find a value for $\epsilon > 0$ for which there is no $\delta$ that satisfies the definition.)

With $f(x)$ defined as: $f(x) = \left\{ \begin{array}{rl} { 4 } &{ \text{if } x < 2 } \\ { 3 } & { \text{if } x > 2 } \end{array}\right.$ show that $\displaystyle\lim_{x\to 2} \, f(x)$ does not exist.
Show that $\displaystyle\lim_{x\to 3} \, \left\lfloor x \right\rfloor$ does not exist.
With $f(x)$ defined as: $f(x) = \left\{ \begin{array}{rl} { x } & { \text{if } x < 2 } \\ { 6-x } & { \text{if } x > 2 } \end{array}\right.$ show that $\displaystyle\lim_{x\to 2} \, f(x)$ does not exist.
With $f(x)$ defined as: $f(x) = \left\{ \begin{array}{rl} { x+1 } & { \text{if } x < 2 } \\ { x^2 } & { \text{if } x > 2 } \end{array}\right.$ show that $\displaystyle\lim_{x\to 2} \, f(x)$ does not exist.
Prove: If $\displaystyle\lim_{x\to a} \, f(x) = L$ and $\displaystyle\lim_{x\to a} g(x) = M$ then $\displaystyle\lim_{x\to a} \, \left[f(x) - g(x)\right] = L-M$.

A Particular Limit	General Limit
\(\displaystyle\lim_{x\to 3} \, 2x - 1 = 5\)	\(\displaystyle\lim_{x\to a} \, f(x) = L\)
“as the values of \(x\) approach \(3\), the values of \(2x-1\) approach (are arbitrarily close to) \(5\)”	“as the values of \(x\) approach \(a\), the values of \(f(x)\) approach (are arbitrarily close to) \(L\)”
“when \(x\) is close to \(3\) (but not equal to \(3\)), the value of \(2x-1\) is close to \(5\)”	“when \(x\) is close to \(a\) (but not equal to \(a\)), the value of \(f(x)\) is close to \(L\)”
“we can guarantee that the values of \(2x-1\) are as close to \(5\) as we want by restricting the values of \(x\) to be sufficiently close to \(3\) (but not equal to \(3\))”	“we can guarantee that the values of \(f(x)\) are as close to \(L\) as we want by restricting the values of \(x\) to be sufficiently close to \(a\)(but not equal to \(a\))”

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Solution

Practice \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Solution

Practice \(\PageIndex{3}\)

Definition of \(\displaystyle\lim_{x\to a} f(x) = L\)

Example \(\PageIndex{4}\)

Solution

Practice \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Solution

Practice \(\PageIndex{5}\)

Theorem

Proof

Example \(\PageIndex{6}\)

Solution

Practice \(\PageIndex{6}\)

Theorem

Proof

Theorem

Proof