2.6: Chain Rule

The Chain Rule is more general than the Inverse Function Rule and deals with the case where \(x\) and \(y\) are both functions of a third variable \(t\). Suppose \[x = f(t), \quad y = G(x). \nonumber\]

Thus \(x\) depends on \(t\), and \(y\) depends on \(x\). But \(y\) is also a function of \(t\), \[y = g(t), \nonumber\]where \(g\) is defined by the rule \[g(t) = G(f(t)). \nonumber\]

The function \(g\) is sometimes called the composition of \(G\) and \(f\) (sometimes written \(g =G \circ f\)).

The composition of \(G\) and \(f\) may be described in terms of black boxes. The function \(g = G \circ f\) is a large black box operating on the input \(t\) to produce \(g(t) = G(f(t))\). If we look inside this black box (pictured in Figure \(\PageIndex{1}\)), we see two smaller black boxes, \(f\) and \(G\). First \(f\) operates on the input \(t\) to produce \(f(t)\), and then \(G\) operates on \(f(t)\) to produce the final output \(g(t) = G(f(t))\).

The Chain Rule expresses the derivative of g in terms of the derivatives of \(f\) and \(G\). It leads to the powerful method of "change of variables" in computing derivatives
and, later on, integrals.

Figure \(\PageIndex{1}\): A composition of two functions.

Chain Rule

Let \(f\), \(G\) be two real functions and define the new function \(g\) by the rule \[g(t) = G(f(t)). \nonumber\]

At any value of \(t\) where the derivatives \(f'(t)\) and \(G'(f(t))\) exist, \(g'(t)\) also exists and has the value \[g'(t) = G'(f(t)) f'(t). \nonumber\]

Proof

Let \(x = f(t), \quad y = g(t), \quad y = G(x)\).

Take \(t\) as the independent variable, and let \(\Delta t \neq 0\) be infinitesimal. Form the corresponding increments \(\Delta x\) and \(\Delta y\). By the Increment Theorem for \(x = f(t)\), \(\Delta x\) is infinitesimal. Using the Increment Theorem again but this time for \(y = G(x)\), we have \[\Delta y = G'(x) \Delta x + \varepsilon \Delta x \nonumber\]

for some infinitesimal \(\varepsilon\). Dividing by \(\Delta t\), \[\frac{\Delta y}{\Delta t} = G'(x) \frac{\Delta x}{\Delta t} + \varepsilon \frac{\Delta x}{\Delta t}. \nonumber\]

Then taking standard parts, \[\begin{align*} st \left(\frac{\Delta y}{\Delta t}\right) &= G'(x) st \left(\frac{\Delta x}{\Delta t}\right) + 0, \\ g'(t) &= G'(x) f'(t) = G'(f(t)) f'(t). \end{align*}\]

Example \(\PageIndex{1}\)

Find the derivative of \(g(t) = \ln (\sin t)\).

Solution

\(g(t)\) is the natural logarithm of the sine of \(t\). It can be written in the form \(g(t) = G(f(t))\) where \[f(t) = \sin t, \quad G(x) = \ln x. \nonumber\]

We have \[f'(t) = \cos t, \quad G'(s) = \frac{1}{x}. \nonumber\]

By the Chain Rule, \[\begin{align*} g'(t) &= G'(f(t)) f'(t) \\ &= \frac{1}{\sin t} \cdot \cos t = \frac{\cos t}{\sin t}. \end{align*}\]

Example \(\PageIndex{2}\)

Find the derivative of \(g(t) = \sqrt{3t + 1}\). 

Solution

\(g(t)\) has the form \(g(t) = G(f(t))\), where \[f(t) = 3t + 1, \quad G(x) = \sqrt{x}. \nonumber\]

We have \[f'(t) = 3, \quad G'(x) = \frac{1}{2} x^{-1/2}. \nonumber\]

Then \[\begin{align*} g'(t) &= G'(f(t)) f'(t) \\ \frac{1}{2} (3t + 1)^{-1/2} \cdot 3 = \frac{3}{2 \sqrt{3t + 1}}. \end{align*}\]

In practice it is more convenient to use the Chain Rule with dependent variables \(x\) and \(y\) instead of functions \(f\) and \(g\).

Chain Rule with Dependent Variables

Let \[x = f(t), \quad y = g(t) = G(x). \nonumber\]

Assume \(g'(t)\) and \(G'(x)\) exist. Then \[(\text{i}) \quad \frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt} \quad\quad (\text{ii}) \quad dy = \frac{dy}{dx} dt \nonumber\]

where \(dx/dt\), \(dy/dt\) are computed with \(t\) as the independent variable, and \(dy/dx\) is computed with \(x\) as the independent variable.

Let us work Examples \(\PageIndex{1}\) and \(\PageIndex{2}\) again with dependent variables.

Example \(\PageIndex{1}\) continued

Let \(x = \sin t, \quad y = \ln x\).

Find \(dy/dt\) using Chain Rule \((\text{i})\) and \(dy\) by using Chain Rule \((\text{ii})\). 

\[\begin{align*} &(\text{i}) \quad\quad\quad &&\frac{dx}{dt} = \cos t, \quad \frac{dy}{dx} = \frac{1}{x}, \\[4pt] &&&\frac{dy}{dt} = \frac{dy}{dx} \cdot \frac{dx}{dt} = \frac{1}{x} \cdot \cos t = \frac{\cos t}{\sin t}. \\[4pt] &(\text{ii}) \quad\quad\quad &&dx = \cos t \ dt, \quad \frac{dy}{dx} = \frac{1}{x}, \\[4pt] &&& dy = \frac{1}{x} \ dx = \frac{1}{x} \cos t \ dt = \frac{\cos t}{\sin t} \ dt. \end{align*}\]

Example \(\PageIndex{2}\) continued

Let \(x = 3t + 1, \quad y = \sqrt{x}\).

\[\begin{align*} &(\text{i}) \quad\quad\quad &&\frac{dx}{dt} 3, \quad \frac{dy}{dx} = \frac{1}{2} x^{-1/2}, \\[4pt] &&&\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt} = \frac{3}{2} x^{-1/2} = \frac{3}{2} (3t + 1)^{-1/2}. \\[4pt] &(\text{ii}) \quad\quad\quad &&dx = 3 \ dt, \quad \frac{dy}{dx} = \frac{1}{2} x^{-1/2}, \\[4pt] &&& dy = \frac{1}{2} x^{-1/2} \ dx = \frac{1}{2} (3t + 1)^{-1/2} \cdot 3 \ dt = \frac{3}{2} (3t + 1)^{-1/2} \ dt. \end{align*}\]

The equation \[\frac{dy}{dt} = \frac{dy}{dt} \frac{dx}{dt} \nonumber\]

with \(t\) as the independent variable is trivial. We simply cancel the \(dx\) instances. But when \(dy/dx\) is computed with \(x\) as the independent variable while \(dx/dt\) is computed with \(t\) as the independent variable, each \(dx\) has a different meaning, and the equation is not trivial.

Similarly, the equation \[dy = \frac{dy}{dx} dx \nonumber\]is trivial with \(x\) as the independent variable but not when \(t\) is the independent variable in \(dy\) and \(dx\), while \(x\) is independent in \(dy/dx\).

The Chain Rule shows that when we change independent variables the equations \[\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt}, \quad dy = \frac{dy}{dx} \ dx \nonumber\]remain true.

The Inverse Function Rule can be proved from the Chain Rule as follows. Let \[y = f(x), \quad x = g(y) \nonumber\]be inverse functions whose derivatives exist. Then \[\frac{dy}{dx} \frac{dx}{dt} = \frac{dy}{dy} = 1, \nonumber\]

whence \[\frac{dy}{dx} = \frac{1}{dx/dy}, \quad f'(x) = \frac{1}{g'(y)}. \nonumber\]

Using the Chain Rule we may write the Power Rule in a general form.

Power Rule

Let \(r\) be a rational number, and let \(u\) depend on \(x\). If \(u > 0\) and \(du/dx\) exists, then \[\frac{d \left(u^{r}\right)}{dx} = ru^{r-1} \frac{du}{dx}. \nonumber\]

This is proved by letting \(y = u^{r}\) and computing \(dy/dx\) by the Chain Rule. \[\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} = ru^{r-1} \frac{du}{dx}. \nonumber\]

The Chain Rule has two types of applications.

(1) Given \(x = f(t)\) and \(y = G(x)\), find \(\dfrac{dy}{dt}\). Use \(\dfrac{dy}{dt} = \dfrac{dy}{dx} \dfrac{dx}{dt}\).

(2) Given \(x = f(t)\) and \(y = g(t)\), find \(\dfrac{dy}{dx}\). Use \(\dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt}\).

Applications of type (1) often arise when a new dependent variable \(x\) is introduced to help compute \(\frac{dy}{dt}\). Applications of type (2) arise when two variables \(x\) and \(y\) both depend on a third variable \(t\), for example, when \(x\) and \(y\) are the coordinates of a moving particle and \(t\) is time.

We give three examples of type (1) and then three of type (2).

Example \(\PageIndex{3}\)

Suppose that by investing \(t\) dollars a company can produce \[x = \frac{t}{10} - 100, \quad t \geq 1000, \nonumber\]

items, and that it can sell \(x\) items for a total profit of \[y = 5x - \frac{x^{2}}{100}. \nonumber\]

Find \(\dfrac{dy}{dt}\), which is the marginal profit with respect to the amount invested.

Solution

We have \[\frac{dx}{dt} = \frac{1}{10}, \quad \frac{dy}{dx} = 5 - \frac{x}{50}. \nonumber\]

By the Chain Rule, \[\begin{align*} \frac{dy}{dt} &= \frac{dy}{dx} \frac{dx}{dt} = \left(5 - \frac{x}{50}\right) \frac{1}{10} \\ &= \left(5 - \frac{\frac{t}{10} - 100}{50}\right) \frac{1}{10} \\ &= 0.7 - \frac{t}{5000}. \end{align*}\]

Thus after \(t\) dollars have been invested, an additional dollar will bring \(0.7 - t/5000\) dollars of additional profit.

Example \(\PageIndex{4}\)

Find \(dy/dt\) where \(y = \left(5t^{2} - 2\right)^{1/4}\).

Solution

Let \[x = 5t^{2} - 2, \quad y = x^{1/4}. \nonumber\]

Then \[\begin{align*} \frac{dx}{dt} &= 10t, \quad \frac{dy}{dx} = \frac{1}{4} x^{-3/4}, \\[4pt] \frac{dy}{dt} &= \frac{dy}{dx} \frac{dx}{dt} = \left(\frac{1}{4} x^{-3/4}\right) (10t) \\ &= \frac{10}{4} \left(5t^{2} - 2\right)^{-3/4} t. \end{align*}\]

Example \(\PageIndex{5}\)

Find \(dy/dx\) where \(y = \sqrt{\sin (4x+1) + \cos (4x-1)}\). 

Solution

This problem requires three uses of the Chain Rule. Let \[u = \sin (4x+1) + \cos (4x-1), \quad y = \sqrt{u}. \nonumber\]

Then by the Chain Rule, \[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = \frac{1}{2\sqrt{u}} \cdot \frac{du}{dx}. \nonumber\]

Now let \[v = \sin (4x+1), \quad w = \cos (4x-1), \quad u = v + w. \nonumber\]

Then \[\frac{du}{dx} = \frac{dv}{dx} + \frac{dw}{dx}. \nonumber\]

We use the Chain Rule twice more to find \(dv/dx\) and \(dw/dx\). \[\begin{align*} v &= \sin (4x+1). \\[4pt] \frac{dv}{dx} &= \cos (4x+1) \frac{d (4x+1)}{dx} = 4 \cos (4x+1). \\ w &= \cos (4x-1). \\ \frac{dw}{dx} &= -\sin (4x-1) \frac{d (4x-1)}{dx} = -4 \sin (4x-1). \end{align*}\]

Finally, we combine everything to get \[\begin{align*} \frac{dy}{dx} &= \frac{1}{2 \sqrt{u}} \cdot \frac{du}{dx} = \frac{1}{2 \sqrt{u}} \left(\frac{dv}{dx} + \frac{dw}{dx}\right) \\ &= \frac{4 \cos (4x+1) - 4 \sin (4x-1)}{2 \sqrt{\sin (4x+1) + \cos (4x-1)}}. \end{align*}\] 

If a particle is moving in the plane, its position \((x, y)\) at time \(t\) will be given by a pair of equations \[x = f(t), \quad y = g(t). \nonumber\]

These are called parametric equations. The slope of the curve traced out by this particle can be found by the Chain Rule, \[\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{g'(t)}{f'(t)}, \nonumber\]whenever the derivatives exist and \(f'(t) \neq 0\). This is a Chain Rule application of type (2).

Example \(\PageIndex{6}\)

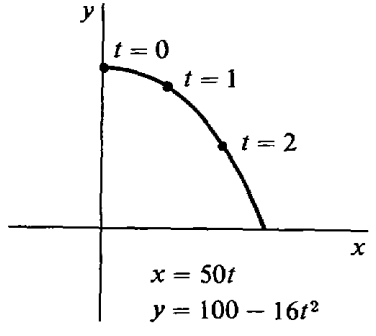
A ball thrown horizontally from a 100-foot cliff at a velocity of 50 ft/sec will follow the parametric equations \[x = 50t, \quad y = 100 - 16t^{2}, \quad \text{in feet}. \nonumber\]Find the slope of its path at time \(t\) (Figure \(\PageIndex{2}\)).

Solution

\[\frac{dx}{dt} = 50, \quad \frac{dy}{dt} = -32t, \nonumber\]

so \[\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = - \frac{32t}{50}. \nonumber\]

Figure \(\PageIndex{2}\): Graph of the ball's path in time.

Example \(\PageIndex{7}\)

A particle moves according to the parametric equations \[x = t^{3} - t, \quad y = t^{2}. \nonumber\]Find the slope of its path.

Solution

\[\frac{dx}{dt} = 3t^{2} - 1, \quad \frac{dy}{dt} = 2t. \nonumber\]

Therefore, \[\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{2t}{3t^{2} - 1}, \quad t \neq \pm \sqrt{1/3}. \nonumber\]

We see from Figure \(\PageIndex{3}\) that the path of this particle is not the graph of a function, and in fact contains a loop and crosses the point \((0, 1)\) twice, at \(t = -1\) and \(t = 1\). The path is vertical at the points \(t = \pm \sqrt{1/3}\), where there is no slope. At the point \((0, 1)\), the two slopes of the path are \(dy/dx = -1\) when \(t = -1\), and \(dy/dx = 1\) when \(t = 1\).

Figure \(\PageIndex{3}\): Graphs of the particle's path in time.

Example \(\PageIndex{8}\)

A particle moving according to the parametric equations \[x = \cos t, \quad y = \sin t \nonumber\]will move counterclockwise around the unit circle at one radian per second beginning at the point \((1, 0)\), as shown in Figure \(\PageIndex{4}\). Find the slope of its path at time \(t\).

Figure \(\PageIndex{4}\): Path in time of a particle moving around the unit circle.

Solution

\[\frac{dx}{dt} = -\sin t, \quad \frac{dy}{dt} = \cos t. \nonumber\]

The slope is \[\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = - \frac{\cos t}{\sin t}. \nonumber\]

In terms of \(x\) and \(y\) the slope is \[\frac{dy}{dx} = - \frac{x}{y}. \nonumber\]

Problems for Section 2.6

In Problems 1-44, find \(dy/dx\).I 

1.	\(y = \sqrt{x + 2}\)	2.	\(y = \sqrt{7 + 4x}\)
3.	\(y = \sqrt{5 - x}\)	4.	\(y = \sqrt{1 - 10x}\)
5.	\(y = \dfrac{1}{\sqrt{2 + 3x}}\)	6.	\(y = \dfrac{1}{\sqrt{4 - x}}\)
7.	\(y = \sqrt[3]{6x + 1}\)	8.	\(y = \sqrt[5]{2 - 3x}\)
9.	\(y = \sqrt{x^{2} + 1}\)	10.	\(y = \sqrt{1 - x^{2}}\)
11.	\(y = \sin (3x)\)	12.	\(y = \cos (4-2x)\)
13.	\(y = \sin \left(x^{-2}\right)\)	14.	\(y = \cos \sqrt{x}\)
15.	\(y = e^{4x}\)	16.	\(y = e^{-x^{2}}\)
17.	\(y = e^{\cos x}\)	18.	\(y = \ln (\ln x)\)
19.	\(y = \cos u, \quad u = e^{x}\)	20.	\(y = \tan u, \quad u = \ln x\)
21.	\(y = u^{10}, \quad 1 - 4x\)	22.	\(y = u^{-10}, \quad 1 - x^{2}\)
23.	\(y = \sin u + \sin v, \quad u = 1 - x^{2}, \quad v = 2x - 1\)
24.	\(y = e^{u} + e^{v}, \quad 1 - 3x, \quad v = 3 - 4x\)
25.	\(y = e^{u}, \quad u = \sqrt{v}, \quad v = \sin x\)
26.	\(y = \ln u, \quad u = \tan v, \quad v = 1/x\)
27.	\(y = u^{-1/3}, \quad u = 1 + \sqrt{v}, \quad v = x^{2} - 1\)
28.	\(y = u^{-1}, \quad u = 3v + 4, \quad v = 1/(x + 1)\)
29.	\(y = u^{4}, \quad u = 1 + 1/v, \quad v = x^{3} + 1\)
30.	\(y = u^{2} + 1, \quad u = v^{2} + 1, \quad v = x^{2} + 1\)
31.	\(y = \left(\sqrt{x^{2} + 1} + \sqrt{x^{2} + 1}\right)^{1/3}\)	32.	\(y = \left(x + \sqrt{3 - 4x}\right)^{-1/2}\)
33.	\(y = 3x \sin (2x - 1)\)	34.	\(y = \sin (2x) \cos (3x)\)
35.	\(x = \cos (3t), \quad y = \sin (3t)\)	36.	\(x = e^{t}, \quad y = \ln t\)
37.	\(x = \sin t, \quad y = \sin (2t)\)	38.	\(x = \sin (e^{t}), \quad y = \cos (e^{t})\)
39.	\(x = \ln (t + 1), \quad y = t^{2}\)	40.	\(x = e^{\cos t}, \quad y = e^{\sin t}\)
41.	\(x = \sqrt{t^{2} - 4}, \quad y = t^{2}\)	42.	\(x = 1 + \sqrt[3]{t}, \quad y = 2 + \sqrt[3]{t}\)
43.	\(x = \sqrt[3]{t + 1}, \quad y = \sqrt[3]{t + 2}\)	44.	\(x = \dfrac{2t + 1}{t + 2}, \quad y = \dfrac{2t + 3}{t + 2}\)
45.	A particle moves in the plane according to the parametric equations \[x = t^{2} + 1, \quad y = 3t^{3}. \nonumber\]Find the slope of its path.
46.	An ant moves in the plane according to the equations \[x = \left(1 - t^{2}\right)^{-1}, \quad y = \sqrt{t}. \nonumber\]Find the slope of its path.
\(\square\) 47.	Let \(y\) depend on \(u\), \(u\) depend on \(v\), and \(v\) depend on \(x\). Assume the derivatives \(dy/du\), \(du/dv\), and \(dv/dx\) exist. Prove that \[\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dv} \frac{dv}{dx}. \nonumber\]
\(\square\) 48.	Let the function \(f(x)\) be differentiable for all \(x\), and let \(g(x) = f(f(x))\). Show that \(g'(x) = f'(f(x)) f'(x)\).