7.2E: Exercises for Section 11.1

Last updated
Save as PDF

Page ID: 70647

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 4, sketch the curves below by eliminating the parameter $t$. Give the orientation of the curve.

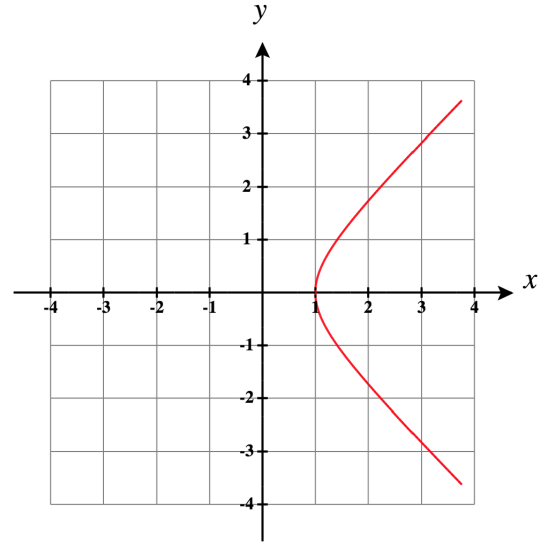
1) $ x=t^2+2t, \quad y=t+1$

Answer

Orientation: bottom to top

$A parabola open to the right with (−1, 0) being the point furthest the left with arrow going from the bottom through (−1, 0) and up.$

2) $ x=\cos(t), \quad y=\sin(t), \quad \text{for } (0,2π]$

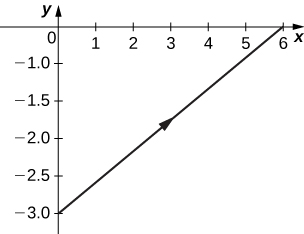
3) $ x=2t+4, \quad y=t−1$

Answer

Orientation: left to right

$A straight line passing through (0, −3) and (6, 0) with arrow pointing up and to the right.$

4) $ x=3−t, \quad y=2t−3, \quad \text{for }1.5≤t≤3$

In exercise 5, eliminate the parameter and sketch the graph.

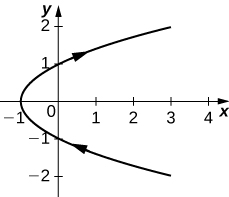
5) $x=2t^2,\quad y=t^4+1$

Answer

$ y=\dfrac{x^2}{4}+1$

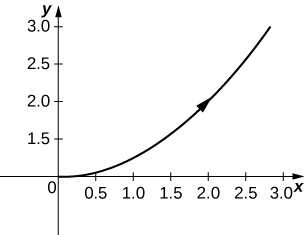
$Half a parabola starting at the origin and passing through (2, 2) with arrow pointed up and to the right.$

In exercises 6 - 9, use technology (CAS or calculator) to sketch the parametric equations.

6) [T] $x=t^2+t, \quad y=t^2−1$

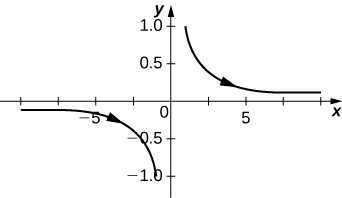
7) [T] $ x=e^{−t}, \quad y=e^{2t}−1$

Answer: $Curve graphed against X and Y axes. The right end of the curve is near point X equals 4, Y equals negative 1. Moving left, the curve rises, slowly at first and then ever faster, as if to asymptotically approach the positive Y axis, although the curve ends near point X equals 1 half, Y equals 6.$

8) [T] $ x=3\cos t, \quad y=4\sin t$

9) [T] $ x=\sec t, \quad y=\cos t$

Answer: $A graph with asymptotes at the x and y axes. There is a portion of the graph in the third quadrant with arrow pointing down and to the right. There is a portion of the graph in the first quadrant with arrow pointing down and to the right.$

In exercises 10 - 20, sketch the parametric equations by eliminating the parameter. Indicate any asymptotes of the graph.

10) $ x=e^t, \quad y=e^{2t}+1$

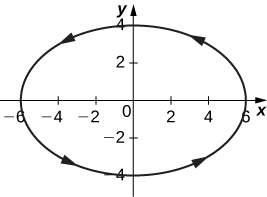
11) $ x=6\sin(2θ), \quad y=-4\cos(2θ)$

Answer: $An ellipse with minor axis vertical and of length 8 and major axis horizontal and of length 12 that is centered at the origin. The arrows go counterclockwise.$

12) $ x=\cos θ, \quad y=2\sin(2θ)$

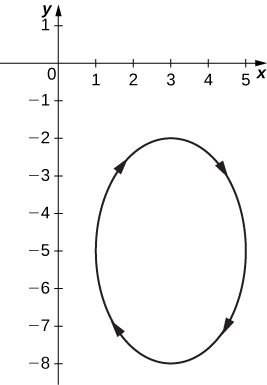
13) $ x=3−2\cos θ, \quad y=−5+3\sin θ$

Answer: $An ellipse in the fourth quadrant with minor axis horizontal and of length 4 and major axis vertical and of length 6. The arrows go clockwise.$

14) $ x=4+2\cos θ, \quad y=−1+\sin θ$

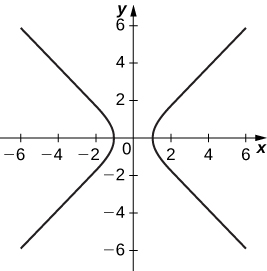
15) $ x=\sec t, \quad y=\tan t$

Answer

Asymptotes are $ y=x$ and $ y=−x$

$A graph with asymptotes at y = x and y = −x. The first part of the graph occurs in the second and third quadrants with vertex at (−1, 0). The second part of the graph occurs in the first and fourth quadrants with vertex as (1, 0).$

16) $ x=\ln(2t), \quad y=t^2$

17) $ x=e^t, \quad y=e^{2t}$

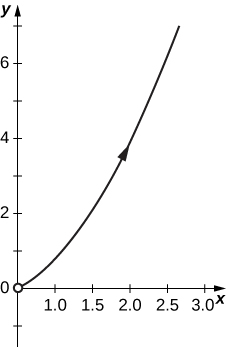
Answer: $A curve starting slightly above the origin and increasing to the right with arrow pointing up and to the right.$

18) $ x=e^{−2t}, \quad y=e^{3t}$

19) $ x=t^3, \quad y=3\ln t$

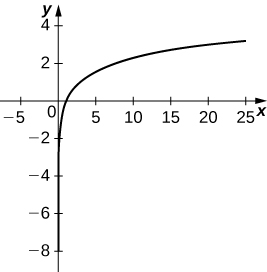
Answer: $A curve with asymptote being the y axis. The curve starts in the fourth quadrant and increases rapidly through (1, 0) at which point is increases much more slowly.$

20) $ x=4\sec θ, \quad y=3\tan θ$

In exercises 21 - 38, convert the parametric equations of a curve into rectangular form. No sketch is necessary. State the domain of the rectangular form.

21) $ x=t^2−1, \quad y=\dfrac{t}{2}$

Answer: $ x=4y^2−1;$ domain: $ x∈[1,∞)$.

22) $ x=\dfrac{1}{\sqrt{t+1}}, \quad y=\dfrac{t}{1+t}, \quad \text{for }t>−1$

23) $ x=4\cos θ, \quad y=3\sin θ, \quad \text{for }t∈(0,2π]$

Answer: $ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1;$ domain $ x∈[−4,4].$

24) $ x=\cosh t, \quad y=\sinh t$

25) $ x=2t−3, \quad y=6t−7$

Answer: $ y=3x+2;$ domain: all real numbers.

26) $ x=t^2, \quad y=t^3$

27) $ x=1+\cos t, \quad y=3−\sin t$

Answer: $ (x−1)^2+(y−3)^2=1$; domain: $ x∈[0,2]$.

28) $ x=\sqrt{t}, \quad y=2t+4$

29) $ x=\sec t, \quad y=\tan t, \quad \text{for } π≤t<\frac{3π}{2}$

Answer: $ y=\sqrt{x^2−1}$; domain: $ x∈(−\infty,-1]$.

30) $ x=2\cosh t, \quad y=4\sinh t$

31) $ x=\cos(2t), \quad y=\sin t$

Answer: $ y^2=\dfrac{1−x}{2};$ domain: $ x∈[-1,1].$

32) $ x=4t+3, \quad y=16t^2−9$

33) $ x=t^2, \quad y=2\ln t, \quad \text{for }t≥1$

Answer: $ y=\ln x;$ domain: $ x∈[1,∞).$

34) $ x=t^3, \quad y=3\ln t, \quad \text{for }t≥1$

35) $ x=t^n, \quad y=n\ln t, \quad \text{for } t≥1,$ where $n$ is a natural number

Answer: $ y=\ln x;$ domain: $ x∈(0,∞).$

36) $ x=\ln(5t), \quad y=\ln(t^2)$ where $ 1≤t≤e$

37) $ x=2\sin(8t), \quad y=2\cos(8t)$

Answer: $ x^2+y^2=4;$ domain: $ x∈[−2,2].$

38) $ x=\tan t, \quad y=\sec^2t−1$

In exercises 39 - 48, the pairs of parametric equations represent lines, parabolas, circles, ellipses, or hyperbolas. Name the type of basic curve that each pair of equations represents.

39) $ x=3t+4, \quad y=5t−2$

Answer: line

40) $ x−4=5t, \quad y+2=t$

41) $ x=2t+1, \quad y=t^2−3$

Answer: parabola

42) $ x=3\cos t, \quad y=3\sin t$

43) $ x=2\cos(3t), \quad y=2\sin(3t)$

Answer: circle

44) $ x=\cosh t, \quad y=\sinh t$

45) $ x=3\cos t, \quad y=4\sin t$

Answer: ellipse

46) $ x=2\cos(3t), \quad y=5\sin(3t)$

47) $ x=3\cosh(4t) \quad y=4\sinh(4t)$

Answer: the right branch of a horizontally opening hyperbola

48) $ x=2\cosh t, \quad y=2\sinh t$

49) Show that $ x=h+r\cos θ, \quad y=k+r\sin θ$ represents the equation of a circle.

50) Use the equations in the preceding problem to find a set of parametric equations for a circle whose radius is $5$ and whose center is $ (−2,3)$.

In exercises 51 - 53, use a graphing utility to graph the curve represented by the parametric equations and identify the curve from its equation.

51) [T] $ x=θ+\sin θ, \quad y=1−\cos θ$

Answer

The equations represent a cycloid.

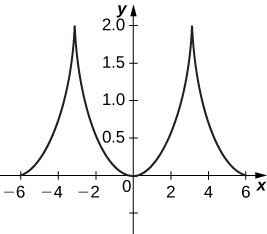
$A graph starting at (−6, 0) increasing rapidly to a sharp point at (−3, 2) and then decreasing rapidly to the origin. The graph is symmetric about the y axis, so the graph increases rapidly to (3, 2) before decreasing rapidly to (6, 0).$

52) [T] $ x=2t−2\sin t, \quad y=2−2\cos t$

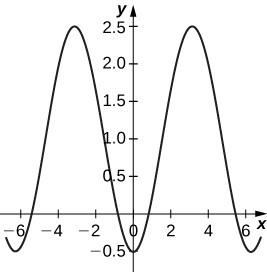
53) [T] $ x=t−0.5\sin t, \quad y=1−1.5\cos t$

Answer: $A graph starting at roughly (−6, 0) increasing to a rounded point and then decreasing to roughly (0, −0.5). The graph is symmetric about the y axis, so the graph increases to a rounded point before decreasing to roughly (6, 0).$

54) An airplane traveling horizontally at 100 m/s over flat ground at an elevation of 4000 meters must drop an emergency package on a target on the ground. The trajectory of the package is given by $ x=100t, \quad y=−4.9t^2+4000, \quad \text{where }t≥0$ where the origin is the point on the ground directly beneath the plane at the moment of release. How many horizontal meters before the target should the package be released in order to hit the target?

55) The trajectory of a bullet is given by $ x=v_0(\cos α)t, \quad y=v_0(\sin α)t−\frac{1}{2}gt^2$ where $ v_0=500$ m/s, $g=9.8=9.8\text{ m/s}^2$, and $ α=30$ degrees. When will the bullet hit the ground? How far from the gun will the bullet hit the ground?

Answer: 22,092 meters at approximately 51 seconds.

56) [T] Use technology to sketch the curve represented by $ x=\sin(4t), \quad y=\sin(3t), \quad \text{for }0≤t≤2π$.

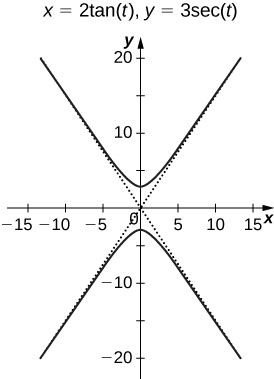
57) [T] Use technology to sketch $ x=2\tan(t), \quad y=3\sec(t), \quad \text{for }−π<t<π.$

Answer: $A graph with asymptotes roughly near y = x and y = −x. The first part of the graph is in the first and second quadrants with vertex near (0, 3). The second part of the graph is in the third and fourth quadrants with vertex near (0, −3).$

58) Sketch the curve known as an epitrochoid, which gives the path of a point on a circle of radius $b$ as it rolls on the outside of a circle of radius $a$. The equations are

$ x=(a+b)\cos t−c⋅\cos\left[\frac{(a+b)t}{b}\right], \quad y=(a+b)\sin t−c⋅\sin\left[\frac{(a+b)t}{b}\right]$.

Let $ a=1,\;b=2,\;c=1.$

59) [T] Use technology to sketch the spiral curve given by $ x=t\cos(t), \quad y=t\sin(t)$ for $ −2π≤t≤2π.$

Answer: $A graph starting at roughly (−6, −1) decreasing to a minimum in the third quadrant near (−1, −4.8) increasing through roughly (0, −4.7) and (3, 0) to a maximum near (1, 1.9) before decreasing through (0, 1.5) to the origin. The graph is symmetric about the y axis, so the graph increases through (0, 1.5) to a maximum in the second quadrant, decreases again through (0, −4.7), and then increases to (6, −1).$

60) [T] Use technology to graph the curve given by the parametric equations $ x=2\cot(t), \quad y=1−\cos(2t), \quad \text{for }−π/2≤t≤π/2.$ This curve is known as the witch of Agnesi.

61) [T] Sketch the curve given by parametric equations $ x=\cosh(t), \quad y=\sinh(t),$ for $ −2≤t≤2.$

Answer: $A vaguely parabolic graph with vertex at the point (1, 0) that opens to the right.$

Search

Text Color

Text Size

Margin Size

Font Type