4.1: Cyclic Subgroups

Often a subgroup will depend entirely on a single element of the group; that is, knowing that particular element will allow us to compute any other element in the subgroup.

Example \(4.1\)

Suppose that we consider \(3 \in {\mathbb Z}\) and look at all multiples (both positive and negative) of \(3\). As a set, this is

\[ 3 {\mathbb Z} = \{ \ldots, -3, 0, 3, 6, \ldots \}\text{.} \nonumber \]

Solution

It is easy to see that \(3 {\mathbb Z}\) is a subgroup of the integers. This subgroup is completely determined by the element \(3\) since we can obtain all of the other elements of the group by taking multiples of \(3\text{.}\) Every element in the subgroup is “generated” by \(3\text{.}\)

Example \(4.2\)

If \(H = \{ 2^n : n \in {\mathbb Z} \}\text{,}\)

Solution

then \(H\) is a subgroup of the multiplicative group of nonzero rational numbers, \({\mathbb Q}^*\text{.}\) If \(a = 2^m\) and \(b = 2^n\) are in \(H\text{,}\) then \(ab^{-1} = 2^m 2^{-n} = 2^{m-n}\) is also in \(H\text{.}\) By Proposition 3.31, \(H\) is a subgroup of \({\mathbb Q}^*\) determined by the element \(2\text{.}\)

Theorem \(4.3\)

Let \(G\) be a group and \(a\) be any element in \(G\text{.}\) Then the set

\[ \langle a \rangle = \{ a^k : k \in {\mathbb Z} \} \nonumber \]

is a subgroup of \(G\text{.}\) Furthermore, \(\langle a \rangle\) is the smallest subgroup of \(G\) that contains \(a\text{.}\)

Proof

The identity is in \(\langle a \rangle \) since \(a^0 = e\text{.}\) If \(g\) and \(h\) are any two elements in \(\langle a \rangle \text{,}\) then by the definition of \(\langle a \rangle\) we can write \(g = a^m\) and \(h = a^n\) for some integers \(m\) and \(n\text{.}\) So \(gh = a^m a^n = a^{m+n}\) is again in \(\langle a \rangle \text{.}\) Finally, if \(g = a^n\) in \(\langle a \rangle \text{,}\) then the inverse \(g^{-1} = a^{-n}\) is also in \(\langle a \rangle \text{.}\) Clearly, any subgroup \(H\) of \(G\) containing \(a\) must contain all the powers of \(a\) by closure; hence, \(H\) contains \(\langle a \rangle \text{.}\) Therefore, \(\langle a \rangle \) is the smallest subgroup of \(G\) containing \(a\text{.}\)

Remark \(4.4\)

If we are using the “+” notation, as in the case of the integers under addition, we write \(\langle a \rangle = \{ na : n \in {\mathbb Z} \}\text{.}\)

For \(a \in G\text{,}\) we call \(\langle a \rangle \) the cyclic subgroup generated by \(a\text{.}\) If \(G\) contains some element \(a\) such that \(G = \langle a \rangle \text{,}\) then \(G\) is a cyclic group. In this case \(a\) is a generator of \(G\text{.}\) If \(a\) is an element of a group \(G\text{,}\) we define the order of \(a\) to be the smallest positive integer \(n\) such that \(a^n= e\text{,}\) and we write \(|a| = n\text{.}\) If there is no such integer \(n\text{,}\) we say that the order of \(a\) is infinite and write \(|a| = \infty\) to denote the order of \(a\text{.}\)

Example \(\PageIndex{1}\)

Notice that a cyclic group can have more than a single generator. Both \(1\) and \(5\) generate \({\mathbb Z}_6\text{;}\)

Solution

hence, \({\mathbb Z}_6\) is a cyclic group. Not every element in a cyclic group is necessarily a generator of the group. The order of \(2 \in {\mathbb Z}_6\) is \(3\text{.}\) The cyclic subgroup generated by \(2\) is \(\langle 2 \rangle = \{ 0, 2, 4 \}\text{.}\)

The groups \({\mathbb Z}\) and \({\mathbb Z}_n\) are cyclic groups. The elements \(1\) and \(-1\) are generators for \({\mathbb Z}\text{.}\) We can certainly generate \({\mathbb Z}_n\) with 1 although there may be other generators of \({\mathbb Z}_n\text{,}\) as in the case of \({\mathbb Z}_6\text{.}\)

Example \(4.6\)

The group of units, \(U(9)\text{,}\) in \({\mathbb Z}_9\) is a cyclic group.

Solution

As a set, \(U(9)\) is \(\{ 1, 2, 4, 5, 7, 8 \}\text{.}\) The element 2 is a generator for \(U(9)\) since

\begin{align*} 2^1 & = 2 \qquad 2^2 = 4\\ 2^3 & = 8 \qquad 2^4 = 7\\ 2^5 & = 5 \qquad 2^6 = 1\text{.} \end{align*}

Example \(4.7\)

Not every group is a cyclic group. Consider the symmetry group of an equilateral triangle \(S_3\text{.}\) The multiplication table for this group is \(Figure \text { } 3.7\).

Solution

The subgroups of \(S_3\) are shown in \(Figure \text { } 4.8\). Notice that every subgroup is cyclic; however, no single element generates the entire group.

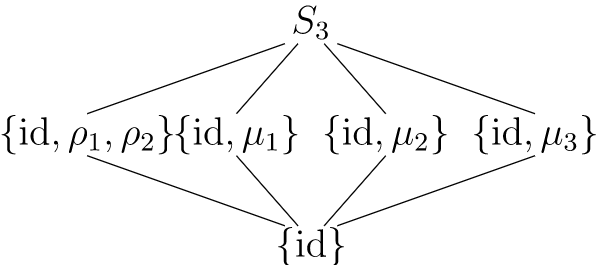
\(Figure \text { } 4.8.\) Subgroups of \(S_3\)

Theorem \(4.9\)

Every cyclic group is abelian.

Proof

Let \(G\) be a cyclic group and \(a \in G\) be a generator for \(G\text{.}\) If \(g\) and \(h\) are in \(G\text{,}\) then they can be written as powers of \(a\text{,}\) say \(g = a^r\) and \(h = a^s\text{.}\) Since

\[ g h = a^r a^s = a^{r+s} = a^{s+r} = a^s a^r = h g\text{,} \nonumber \]

\(G\) is abelian.

Subgroups of Cyclic Groups

We can ask some interesting questions about cyclic subgroups of a group and subgroups of a cyclic group. If \(G\) is a group, which subgroups of \(G\) are cyclic? If \(G\) is a cyclic group, what type of subgroups does \(G\) possess?

Theorem \(4.10\)

Every subgroup of a cyclic group is cyclic.

Proof

The main tools used in this proof are the division algorithm and the Principle of Well-Ordering. Let \(G\) be a cyclic group generated by \(a\) and suppose that \(H\) is a subgroup of \(G\text{.}\) If \(H = \{ e \}\text{,}\) then trivially \(H\) is cyclic. Suppose that \(H\) contains some other element \(g\) distinct from the identity. Then \(g\) can be written as \(a^n\) for some integer \(n\text{.}\) Since \(H\) is a subgroup, \(g^{-1} = a^{-n}\) must also be in \(H\text{.}\) Since either \(n\) or \(-n\) is positive, we can assume that \(H\) contains positive powers of \(a\) and \(n \gt 0\text{.}\) Let \(m\) be the smallest natural number such that \(a^m \in H\text{.}\) Such an \(m\) exists by the Principle of Well-Ordering.

We claim that \(h = a^m\) is a generator for \(H\text{.}\) We must show that every \(h' \in H\) can be written as a power of \(h\text{.}\) Since \(h' \in H\) and \(H\) is a subgroup of \(G\text{,}\) \(h' = a^k\) for some integer \(k\text{.}\) Using the division algorithm, we can find numbers \(q\) and \(r\) such that \(k = mq +r\) where \(0 \leq r \lt m\text{;}\) hence,

\[ a^k = a^{mq +r} = (a^m)^q a^r = h^q a^r\text{.} \nonumber \]

So \(a^r = a^k h^{-q}\text{.}\) Since \(a^k\) and \(h^{-q}\) are in \(H\text{,}\) \(a^r\) must also be in \(H\text{.}\) However, \(m\) was the smallest positive number such that \(a^m\) was in \(H\text{;}\) consequently, \(r=0\) and so \(k=mq\text{.}\) Therefore,

\[ h' = a^k = a^{mq} = h^q \nonumber \]

and \(H\) is generated by \(h\text{.}\)

Corollary \(4.11\)

The subgroups of \({\mathbb Z}\) are exactly \(n{\mathbb Z}\) for \(n = 0, 1, 2,\ldots\text{.}\)

Proposition \(4.12\)

Let \(G\) be a cyclic group of order \(n\) and suppose that \(a\) is a generator for \(G\text{.}\) Then \(a^k=e\) if and only if \(n\) divides \(k\text{.}\)

Proof

First suppose that \(a^k=e\text{.}\) By the division algorithm, \(k = nq + r\) where \(0 \leq r \lt n\text{;}\) hence,

\[ e = a^k = a^{nq + r} = a^{nq} a^r = e a^r = a^r\text{.} \nonumber \]

Since the smallest positive integer \(m\) such that \(a^m = e\) is \(n\text{,}\) \(r= 0\text{.}\)

Conversely, if \(n\) divides \(k\text{,}\) then \(k=ns\) for some integer \(s\text{.}\) Consequently,

\[ a^k = a^{ns} = (a^n)^s = e^s = e\text{.} \nonumber \]

Theorem \(4.13\)

Let \(G\) be a cyclic group of order \(n\) and suppose that \(a \in G\) is a generator of the group. If \(b = a^k\text{,}\) then the order of \(b\) is \(n/d\text{,}\) where \(d = \gcd(k,n)\text{.}\)

Proof

We wish to find the smallest integer \(m\) such that \(e = b^m = a^{km}\text{.}\) By Proposition 4.12, this is the smallest integer \(m\) such that \(n\) divides \(km\) or, equivalently, \(n/d\) divides \(m(k/d)\text{.}\) Since \(d\) is the greatest common divisor of \(n\) and \(k\text{,}\) \(n/d\) and \(k/d\) are relatively prime. Hence, for \(n/d\) to divide \(m(k/d)\) it must divide \(m\text{.}\) The smallest such \(m\) is \(n/d\text{.}\)

Corollary \(4.14\)

The generators of \({\mathbb Z}_n\) are the integers \(r\) such that \(1 \leq r \lt n\) and \(\gcd(r,n) = 1\text{.}\)

Example \(\PageIndex{1}\)

Let us examine the group \({\mathbb Z}_{16}\text{.}\)

Solution

The numbers \(1\text{,}\) \(3\text{,}\) \(5\text{,}\) \(7\text{,}\) \(9\text{,}\) \(11\text{,}\) \(13\text{,}\) and \(15\) are the elements of \({\mathbb Z}_{16}\) that are relatively prime to \(16\text{.}\) Each of these elements generates \({\mathbb Z}_{16}\text{.}\) For example,

\begin{align*} 1 \cdot 9 & = 9 & 2 \cdot 9 & = 2 & 3 \cdot 9 & = 11\\ 4 \cdot 9 & = 4 & 5 \cdot 9 & = 13 & 6 \cdot 9 & = 6\\ 7 \cdot 9 & = 15 & 8 \cdot 9 & = 8 & 9 \cdot 9 & = 1\\ 10 \cdot 9 & = 10 & 11 \cdot 9 & = 3 & 12 \cdot 9 & = 12\\ 13 \cdot 9 & = 5 & 14 \cdot 9 & = 14 & 15 \cdot 9 & = 7\text{.} \end{align*}