2.5: Group Tables

Recall that we could represent a binary operation on a finite set using a table. Since groups have binary operations at their core, we can represent a finite group (i.e., a group with finitely many elements) using a table, called a group table. For example, the group table for \(D_3\) is given below, where we have used \(\{r,s\}\) as the generating set (see Problem 2.4.2).

\(\begin{array}{c|c|c|c|c|c|c}
* & e & r & r^{2} & s & s r & s r^{2} \\
\hline e & e & r & r^{2} & s & s r & s r^{2} \\
\hline r & r & r^{2} & e & s r^{2} & s & s r \\
\hline r^{2} & r^{2} & e & r & s r & s r^{2} & s \\
\hline s & s & s r & s r^{2} & e & r & r^{2} \\
\hline s r & s r & s r^{2} & s & r^{2} & e & r \\
\hline s r^{2} & s r^{2} & s & s r & r & r^{2} & e
\end{array}\)

As a reminder, our convention is that if \(x\) appears in row \(i\) and \(y\) appears in column \(j\), then row \(i\) “times" column \(j\) will result in the element determined by \(xy\), where as usual we follow our right to left convention. That is, \(xy\) means we apply \(y\) first and then \(x\) (as in function composition).

Given an arbitrary group \(G\), we should probably say, “a group table for \(G\)" and not “the group table for \(G\)." The reason for this is that if we chose a different order of the elements (e.g., swap rows 1 and 4—which swaps columns 1 and 4, as well), then the table would look slightly different. Also, if we had chosen a different generating set, then the names of the elements would look different. Regardless, the table still captures the same information about the binary operation. Because every possible table for a given group conveys the same information about the architecture of the group, people may refer to any table for the group as “the" table. Regardless of the ordering of the other elements in the group, it is standard practice to list the identity first. That is, we will always put \(e\) in the top row and the leftmost column.

Problem \(\PageIndex{1}\)

For each of the following groups, identify a generating set and then create the group table.

1. \(R_4\)
2. \(D_4\)
3. \(S_3\)

Problem \(\PageIndex{2}\)

Given the table for a group, how can you identify which elements are inverses of each other? Does this tell you anything about which element must appear in every row and column of the group table?

Let’s introduce a couple of new groups.

Problem \(\PageIndex{3}\): Introducing \(S_2\)

Consider the symmetric group \(S_2\) that consists of the net actions that permute the positions of two coins (without flipping them over) that are sitting side by side in a line. Let \(s\) be the action that swaps the positions of the two coins.

1. Verify that \(S_2=\langle s\rangle\). What is the order of \(S_2\)?
2. Create the group table for \(S_2\).
3. Is \(S_2\) abelian?

Problem \(\PageIndex{4}\): Klein group

Consider a rectangle (which may or may not be a square) oriented so that one side is parallel to the ground. Let \(h\) be the symmetry that reflects the rectangle over the horizontal midline and let \(v\) be the symmetry that reflects the rectangle over the vertical midline. Define \(V_4:=\langle v, h\rangle\). This group is called the Klein group (or Vierergruppe, which is German for “four-group") after the German mathematician Felix Klein (1849–1925).

1. Verify that \(|V_4|=4\) by describing the symmetries in the group.
2. Create the group table for \(V_4\).
3. Is \(V_4\) abelian?
4. Is \(V_4\) cyclic?

Perhaps you noticed when creating the tables above that each element of the group appeared exactly once in each row and column, respectively. This is true in general for groups.

Theorem \(\PageIndex{1}\)

If \((G,*)\) is a finite group, then each element of \(G\) appears exactly once in each row and each column, respectively, in any group table for \(G\).

We can also use tables to define groups. For example, consider the following table on the set \(A=\{e,a,b,c\}\).

\(\begin{array}{c|c|c|c|c}
* & e & a & b & c \\
\hline e & e & a & b & c \\
\hline a & a & e & c & b \\
\hline b & b & c & e & a \\
\hline c & c & b & a & e
\end{array}\)

Is this a table for a group? First, we see that the binary operation determined by the table is closed. Second, we see that \(e\) is acting as the identity. Since every row and column has the identity element \(e\) appearing, we know that every element has an inverse (do you see why that follows?). The only thing left to check is associativity. Imagine for a moment what this entails. It’s messy right?! And this is only for a group of order 4.

Thankfully, we can rely on some prior knowledge to help out with associativity. It turns out that if you look closely, the group table for \(V_4\) looks the “same" as the table above. What do we mean by “same" here? The names for elements are different (except for \(e\)), but

the product of corresponding elements yields the corresponding result.

To see what I mean, let’s color both tables with white, red, blue, and green in such a way that each element corresponds to a unique color. If we choose our colors wisely, it is easy to see that both tables have the same structure.

Figure \(\PageIndex{1}\)

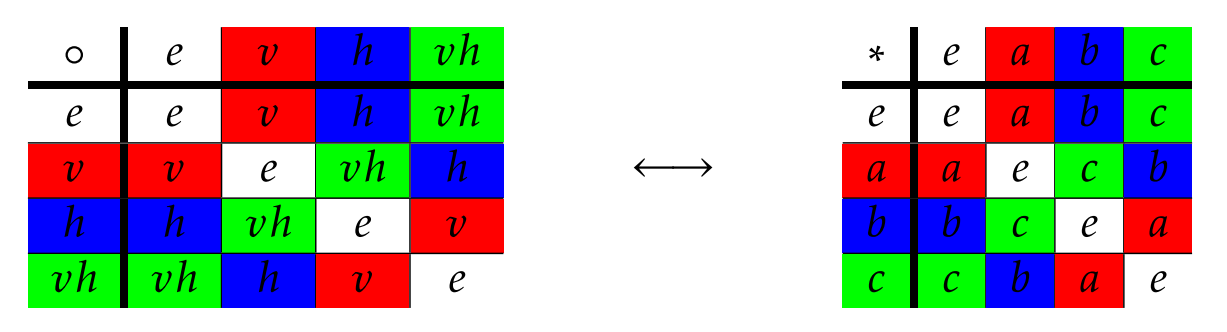
Since we already know that \(V_4\) is a group, we know that the binary operation for \(V_4\) is associative. This discussion verifies that \((A,*)\) is a group.

It is important to point out that if we had not chosen our colors wisely, then perhaps the colorings of the two tables would not agree. Moreover, if we had made the same color choices for elements, but then rearranged columns and rows of one table, the colorings of the two tables would not agree. This doesn’t imply anything. The point is whether we can get the tables to match.

Problem \(\PageIndex{5}\): \(V_4\) Not \(R_4\) Coloring

Is it possible to color the group table for \(R_4\) so that it matches the coloring of \(V_4\)? Explain your answer.