3.1: Subgroups

Problem \(\PageIndex{1}\)

Recall the definition of “subset." What do you think “subgroup" means? Try to come up with a potential definition. Try not to read any further before doing this.

Problem \(\PageIndex{2}\): \(R_4\) in \(D_4\)

Examine your Cayley diagrams for \(D_4\) (with generating set \(\{r,s\}\)) and \(R_4\) (with generating set \(\{r\}\)) and make some observations. How are they similar and how are they different? Can you reconcile the similarities and differences by thinking about the actions of each group?

Hopefully, one of the things you noticed in the previous problem is that we can “see" \(R_4\) inside of \(D_4\). You may have used different colors in each case and maybe even labeled the vertices with different words, but the overall structure of \(R_4\) is there nonetheless.

Problem \(\PageIndex{3}\): \(R_4\) Subgroup \(D_4\)

If you ignore the labels on the vertices and just pay attention to the configuration of arrows, it appears that there are two copies of the Cayley diagram for \(R_4\) in the Cayley diagram for \(D_4\). Isolate these two copies by ignoring the edges that correspond to the generator \(s\). Now, paying close attention to the words that label the vertices from the original Cayley diagram for \(D_4\), are either of these groups in their own right?

Recall that the identity must be one of the elements included in a group. If this didn’t occur to you when doing the previous problem, you might want to go back and rethink your answer. Just like in the previous problem, we can often “see" smaller groups living inside larger groups. These smaller groups are called subgroups.

Definition: Subgroup

Let \(G\) be a group and let \(H\) be a subset of \(G\). Then \(H\) is a subgroup of \(G\), written \(H\leq G\), provided that \(H\) is a group in its own right under the binary operation inherited from \(G\).

The phrase “under the binary operation inherited from \(G\)" means that to combine two elements in \(H\), we should treat the elements as if they were in \(G\) and perform the binary operation of \(G\).

In light of Problem \(\PageIndex{3}\), we would write \(R_4\leq D_4\). The second sub-diagram of the Cayley diagram for \(D_4\) (using \(\{r,s\}\) as the generating set) that resembles \(R_4\) cannot be a subgroup because it does not contain the identity. However, since it looks a lot like \(R_4\), we call it a clone of \(R_4\). For convenience, we also say that a subgroup is a clone of itself.

Problem \(\PageIndex{4}\): Informal Subgroup Criterion

[prob:informal_subgroup_criterion] Let \(G\) be a group and let \(H\subseteq G\). If we wanted to determine whether \(H\) is a subgroup of \(G\), can we skip checking any of the axioms? Which axioms must we verify?

Let’s make the observations of the previous problem a bit more formal.

Theorem \(\PageIndex{1}\): Subgroup Criterion

Suppose \(G\) is a group and \(H\) is a nonempty subset of \(G\). Then \(H\leq G\) if and only if (i) for all \(h\in H\), \(h^{-1} \in H\), as well, and (ii) \(H\) is closed under the binary operation of \(G\).

Notice that one of the hypotheses of Theorem \(\PageIndex{1}\) is that \(H\) be nonempty. This means that if we want to prove that a certain subset \(H\) is a subgroup of a group \(G\), then one of the things we must do is verify that \(H\) is in fact nonempty. In light of this, the “Two Step Subgroup Test" should probably be called the “Three Step Subgroup Test".

As Theorems \(\PageIndex{2}\) and \(\PageIndex{3}\) will illustrate, there are a couple of subgroups that every group contains.

Theorem \(\PageIndex{2}\): Trivial Subgroup

If \(G\) is a group, then \(\{e\}\leq G\).

The subgroup \(\{e\}\) is referred to as the trivial subgroup. All other subgroups are called nontrivial.

Problem \(\PageIndex{5}\)

Let \(G\) be a group. What does the Cayley diagram for the subgroup \(\{e\}\) look like? What are you using as your generating set?

Earlier, we referred to subgroups as being “smaller." However, our definition does not imply that this has to be the case.

Theorem \(\PageIndex{3}\): Improper Subgroup

If \(G\) is a group, then \(G\leq G\).

We refer to subgroups that are not equal to the whole group as proper subgroups. If \(H\) is a proper subgroup, then we may write \(H<G\).

Recall Theorem 2.4.1 that states that if \(G\) is a group under \(*\) and \(S\) is a subset of \(G\), then \(\langle S\rangle\) is also a group under \(*\). Let’s take this a step further.

Theorem \(\PageIndex{4}\): Smallest Subgroup Containing \(S\)

If \(G\) is a group and \(S\subseteq G\), then \(\langle S\rangle \leq G\). In particular, \(\langle S\rangle\) is the smallest subgroup of \(G\) containing \(S\).

The subgroup \(\langle S\rangle\) is called the subgroup generated by \(S\). In the special case when \(S\) equals a single element, say \(S=\{g\}\), then \[\langle g\rangle =\{g^k\mid k\in\mathbb{Z}\},\] which is called the (cyclic) subgroup generated by \(g\). Every subgroup can be written in the “generated by" form. That is, if \(H\) is a subgroup of a group \(G\), then there always exists a subset \(S\) of \(G\) such that \(\langle S\rangle=H\). In particular, \(\langle H\rangle=H\) for \(H\leq G\), and as a special case, we have \(\langle G\rangle=G\).

Problem \(\PageIndex{6}\)

Consider \(\text{Spin}_{1\times 2}\) with generating set \(\{s_{11}, s_{22},s_{12}\}\).

1. Find the Cayley diagram for the subgroup \(\langle s_{11}\rangle\) inside the Cayley diagram for \(\text{Spin}_{1\times 2}\). Identify all of the clones of \(\langle s_{11}\rangle\) inside \(\text{Spin}_{1\times 2}\).
2. Find the Cayley diagram for the subgroup \(\langle s_{11}, s_{22}\rangle\) inside the Cayley diagram of \(\text{Spin}_{1\times 2}\). Identify the clones of \(\langle s_{11}, s_{22}\rangle\) inside \(\text{Spin}_{1\times 2}\).

One of the benefits of Cayley diagrams is that they are useful for visualizing subgroups. However, recall that if we change our set of generators, we might get a very different looking Cayley diagram. The upshot of this is that we may be able to see a subgroup in one Cayley diagram for a given group, but not be able to see it in the Cayley diagram arising from a different generating set.

Problem \(\PageIndex{7}\)

We currently have two different Cayley diagrams for \(D_3\) (see Problems 2.2.5 and 2.4.3).

1. Can you find the Cayley diagram for the trivial subgroup \(\langle e\rangle\) in either Cayley diagram for \(D_3\)? Identify all of the clones of \(\langle e\rangle\) in both Cayley diagrams for \(D_3\).
2. Can you find the Cayley diagram for the subgroup \(\langle r\rangle =R_3\) in either Cayley diagram for \(D_3\)? If possible, identify all of the clones of \(R_3\) in the Cayley diagrams for \(D_3\).
3. Can you find the Cayley diagrams for \(\langle s\rangle\) and \(\langle s'\rangle\) in either Cayley diagram for \(D_3\)? If possible, identify all of the clones of \(\langle s\rangle\) and \(\langle s'\rangle\) in the Cayley diagrams for \(D_3\).

Problem \(\PageIndex{8}\): Subgroups \(D_4\)

Consider \(D_4\). Let \(h\) be the reflection of the square over the horizontal midline and let \(v\) be the reflection over the vertical midline. Which of the following are subgroups of \(D_4\)? In each case, justify your answer. If a subset is a subgroup, try to find a minimal generating set. Also, determine whether you can see the subgroups in our Cayley diagram for \(D_4\) with generating set \(\{r,s\}\).

1. \(\{e, r^2\}\)
2. \(\{e,h\}\)
3. \(\{e, h, v\}\)
4. \(\{e, h, v, r^2\}\)

Perhaps you recognized the set in part d of the previous problem as being the Klein four-group \(V_4\). It follows that \(V_4\leq D_4\).

Let’s introduce a group we haven’t seen yet. Define the quaternion group to be the group \(Q_8=\{1,-1,i,-i,j,-j,k,-k\}\) having the Cayley diagram with generating set \(\{i, j, -1\}\) given in Figure \(\PageIndex{1}\). In this case, 1 is the identity of the group.

Figure \(\PageIndex{1}\): Cayley Diagrem for \(Q_8\)with generating set \(\{-1, i, j\}\)

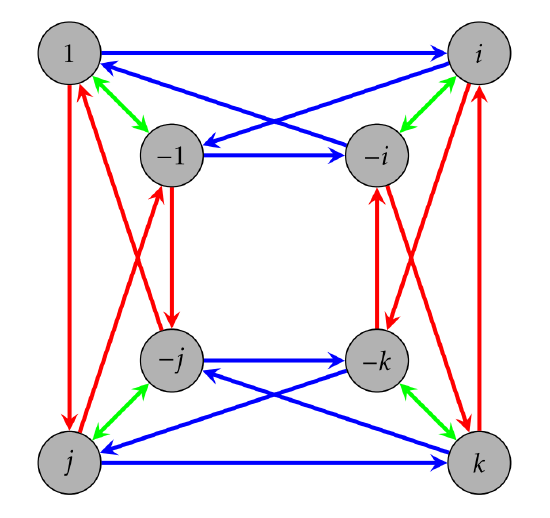
Notice that I didn’t mention what the actions actually do. For now, let’s not worry about that. The relationship between the arrows and vertices tells us everything we need to know. Also, let’s take it for granted that \(Q_8\) actually is a group.

Problem \(\PageIndex{9}\)

Consider the Cayley diagram for \(Q_8\) given in Figure \(\PageIndex{1}\).

1. Which arrows correspond to which generators in our Cayley diagram for \(Q_8\)?
2. What is \(i^2\) equal to? That is, what element of \(\{1,-1,i,-i,j,-j,k,-k\}\) is \(i^2\) equal to? How about \(i^3\), \(i^4\), and \(i^5\)?
3. What are \(j^2\), \(j^3\), \(j^4\), and \(j^5\) equal to?
4. What is \((-1)^2\) equal to?
5. What is \(ij\) equal to? How about \(ji\)?
6. Can you determine what \(k^2\) and \(ik\) are equal to?
7. Can you identify a generating set consisting of only two elements? Can you find more than one?
8. What subgroups of \(Q_8\) can you see in the Cayley diagram in Figure \(\PageIndex{1}\)?
9. Find a subgroup of \(Q_8\) that you cannot see in the Cayley diagram.

Problem \(\PageIndex{10}\)

Consider \((\mathbb{R}^3,+)\), where \(\mathbb{R}^3\) is the set of all 3-entry row vectors with real number entries (e.g., \((a,b,c)\) where \(a,b,c\in\mathbb{R}\)) and \(+\) is ordinary vector addition. It turns out that \((\mathbb{R}^3,+)\) is an abelian group with identity \((0,0,0)\).

1. Let \(H\) be the subset of \(\mathbb{R}^3\) consisting of vectors with first coordinate 0. Is \(H\) a subgroup of \(\mathbb{R}^3\)? Prove your answer.
2. Let \(K\) be the subset of \(\mathbb{R}^3\) consisting of vectors whose entries sum to 0. Is \(K\) a subgroup of \(\mathbb{R}^3\)? Prove your answer.
3. Construct a subset of \(\mathbb{R}^3\) (different from \(H\) and \(K\)) that is not a subgroup of \(\mathbb{R}^3\).

Problem \(\PageIndex{11}\): \(n \mathbb{Z}\)

Consider the group \((\mathbb{Z},+)\) (under ordinary addition).

1. Show that the even integers, written \(2\mathbb{Z}:=\{2k\mid k\in\mathbb{Z}\}\), form a subgroup of \(\mathbb{Z}\).
2. Show that the odd integers are not a subgroup of \(\mathbb{Z}\).
3. Show that all subsets of the form \(n\mathbb{Z}:=\{nk\mid k\in\mathbb{Z}\}\) for \(n\in\mathbb{Z}\) are subgroups of \(\mathbb{Z}\).
4. [prob:nZothers] Are there any other subgroups besides the ones listed in part (c)? Explain your answer.
5. For \(n\in \mathbb{Z}\), write the subgroup \(n\mathbb{Z}\) in the “generated by" notation. That is, find a set \(S\) such that \(\langle S\rangle =n\mathbb{Z}\). Can you find more than one way to do it?

Problem \(\PageIndex{12}\)

Consider the group of symmetries of a regular octagon. This group is denoted by \(D_8\), where the operation is composition of actions. The group \(D_8\) consists of 16 elements (8 rotations and 8 reflections). Let \(H\) be the subset consisting of the following clockwise rotations: \(0^\circ\), \(90^\circ\), \(180^\circ\), and \(270^\circ\). Determine whether \(H\) is a subgroup of \(D_8\) and justify your answer.

Problem \(\PageIndex{13}\)

Consider the groups \((\mathbb{R},+)\) and \((\mathbb{R}\setminus\{0\},\cdot)\). Explain why \(\mathbb{R}\setminus\{0\}\) is not a subgroup of \(\mathbb{R}\) despite the fact that \(\mathbb{R}\setminus\{0\}\subseteq\mathbb{R}\) and both are groups (under the respective binary operations).

Theorem \(\PageIndex{5}\)

If \(G\) is an abelian group such that \(H\leq G\), then \(H\) is an abelian subgroup.

Problem \(\PageIndex{14}\)

Is the converse of the previous theorem true? If so, prove it. Otherwise, provide a counterexample.

As we’ve seen, some groups are abelian and some are not. If \(G\) is a group, then we define the center of \(G\) to be \[Z(G):=\{z\in G\mid zg=gz\text{ for all } g\in G\}.\] Notice that if \(G\) is abelian, then \(Z(G)=G\). However, if \(G\) is not abelian, then \(Z(G)\) will be a proper subset of \(G\). In some sense, the center of a group is a measure of how close \(G\) is to being abelian.

Theorem \(\PageIndex{6}\)

If \(G\) is a group, then \(Z(G)\) is an abelian subgroup of \(G\).

Problem \(\PageIndex{15}\)

Find the center of each of the following groups.

1. \(S_2\)
2. \(V_4\)
3. \(S_3\)
4. \(D_3\)
5. \(D_4\)
6. \(R_4\)
7. \(R_6\)
8. \(\text{Spin}_{1\times 2}\)
9. \(Q_8\)
10. \((\mathbb{Z},+)\)
11. \((\mathbb{R}\setminus\{0\},\cdot)\)