3.2: Subgroup Lattices

One of the goals of this section is to gain better understanding of the structure of groups by studying their subgroups.

Suppose we wanted to find all of the subgroups of a finite group \(G\). Theorems 3.1.2 and 3.1.3 tell us that \(\{e\}\) and \(G\) itself are subgroups of \(G\), but there may be others. Theorem 3.1.1 tells us that if we want to find other subgroups of \(G\), we need to find nonempty subsets of \(G\) that are closed and contain all the necessary inverses. So, one method for finding subgroups would be to find all possible nonempty subsets of \(G\) and then go about determining which subsets are subgroups by verifying whether a given subset is closed under inverses and closed under the operation of \(G\). This is likely to be fairly time consuming.

Another approach would be to utilize the fact that every subgroup \(H\) of \(G\) has a generating set. That is, if \(H\) is a subgroup of a group \(G\), then there always exists a subset \(S\) of \(G\) such that \(\langle S\rangle=H\). Given a subset \(S\) of \(G\), \(\langle S\rangle\) is guaranteed to be closed under inverses and the operation of the group \(G\). So, we could determine all of the subgroups of \(G\) by generating groups with various subsets \(S\) of \(G\). Of course, one drawback is that it might take a bit of effort to determine what \(\langle S\rangle\) actually is. Another drawback is that two different subsets \(S\) and \(T\) may generate the same subgroup.

Let’s make this a bit more concrete by exploring an example. Consider the group \(R_4\). What are the subgroups of \(R_4\)? Since the order of \(R_4\) is 4, we know that there are \(2^4-1=15\) nonempty subsets of \(R_4\). Some of these are subgroups, but most of them are not. Theorems 3.1.2 and 3.1.3 guarantee that \(\{e\}\) and \(R_4\) itself are subgroups of \(R_4\). That’s 2 out of 15 so far. Are there any others? Let’s do an exhaustive search by playing with generating sets. We can certainly be more efficient, but below we list all of the possible subgroups we can generate using subsets of \(R_4\). As you scan the list, you should take a moment to convince yourself that the list is accurate.

\(\begin{array}{ll}
\langle e\rangle=\{e\} & \left\langle r, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\langle r\rangle=\left\{e, r, r^{2}, r^{3}\right\} & \left\langle r^{2}, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\left\langle r^{2}\right\rangle=\left\{e, r^{2}\right\} & \left\langle e, r, r^{2}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\left\langle r^{3}\right\rangle=\left\{e, r^{3}, r^{2}, r\right\} & \left\langle e, r, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\langle e, r\rangle=\left\{e, r, r^{2}, r^{3}\right\} & \left\langle e, r^{2}, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\left\langle e, r^{2}\right\rangle=\left\{e, r^{2}\right\} & \left\langle r, r^{2}, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\} \\
\left\langle e, r^{3}\right\rangle=\left\{e, r^{3}, r^{2}, r\right\} & \left\langle e, r, r^{2}, r^{3}\right\rangle=\left\{e, r, r^{2}, r^{3}\right\}
\end{array}\)

Let’s make a few observations. Scanning the list, we see only three distinct subgroups: \[\{e\}, \{e,r^2\},\{e,r,r^2,r^3\}.\] Out of 15 nonempty subsets of \(R_4\), only 3 subsets are subgroups. Our exhaustive search guarantees that these are the only subgroups of \(R_4\). It is also worth pointing out that if a subset contains either \(r\) or \(r^3\), then that subset generates all of \(R_4\). The reason for this is that \(\{r\}\) and \(\{r^3\}\) are each minimal generating sets for \(R_4\). More generally, observe that if we increase the size of the generating subset using an element that was already contained in the subgroup generated by the set, then we don’t get anything new. For example, consider \(\langle r^2\rangle=\{e,r^2\}\). Since \(e\in\langle r^2\rangle\), we don’t get anything new by including \(e\) in our generating set. We can state this as a general fact.

Theorem \(\PageIndex{1}\)

Let \(G\) be a group and let \(g_1,g_2,\ldots,g_n\in G\). If \(x\in\langle g_1,g_2,\ldots,g_n\rangle\), then \(\langle g_1,g_2,\ldots,g_n\rangle = \langle g_1,g_2,\ldots,g_n,x\rangle\).

In the previous theorem, we are not claiming that \(\{g_1,g_2,\ldots,g_n\}\) is a generating set for \(G\)—although this may be the case. Instead, are simply making a statement about the subgroup \(\langle g_1,g_2,\ldots,g_n\rangle\), whatever it may be.

We can capture the overall relationship between the subgroups of a group \(G\) using a subgroup lattice. Given a group \(G\), the lattice of subgroups of \(G\) is the partially ordered set whose elements are the subgroups of \(G\) with the partial order relation being set inclusion. It is common to depict the subgroup lattice for a group using a Hasse diagram. The Hasse diagram of subgroup lattice is drawn as follows:

1. Each subgroup \(H\) of \(G\) is a vertex.
2. Vertices corresponding to subgroups with smaller order are placed lower in the diagram than vertices corresponding to subgroups with larger order. In particular, the vertex for \(\{e\}\) is placed at the bottom of the diagram and the vertex for \(G\) is placed at the top.
3. There is an edge going up from \(H\) to \(K\) if \(H\leq K\) and there is no subgroup \(L\) such that \(H\leq L\leq K\) with \(L\neq H,K\).

Notice that there is an upward path of edges in the Hasse diagram from \(H\) to \(K\) if and only if \(H\leq K\). For convenience we will not make a distinction between the subgroup lattice for a group \(G\) and the corresponding Hasse diagram.

The Hasse diagram for the subgroup lattice for \(R_4\) is given in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Subgroup Lattice for \(R_4\)

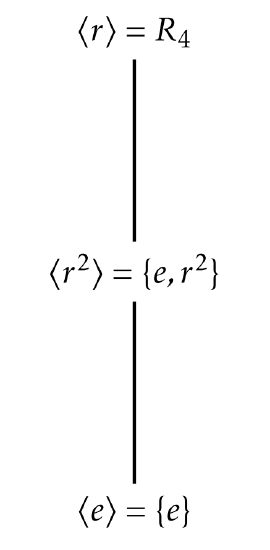
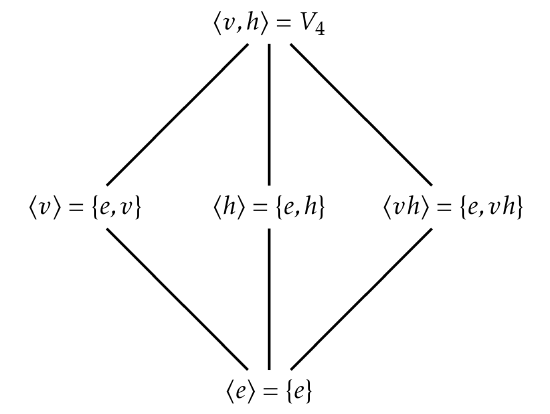
Let’s see what we can do with \(V_4=\{e,v,h,vh\}\). Using an exhaustive search, we find that there are five subgroups:

\(\langle e \rangle = \{e\}\)

\(\langle h \rangle = \{e,h\}\)

\(\langle v \rangle = \{e,v\}\)

\(\langle vh \rangle = \{e,vh\}\)

\(\langle v,h \rangle = \langle v,vh\rangle = \langle h, vh\rangle= \{e,v,h,vh\}=V_4\)

For each subgroup above, we’ve used minimal generating sets to determine the subgroup. The subgroup lattice for \(V_4\) is given in Figure \(\PageIndex{2}\). Notice that there are no edges among \(\langle v\rangle, \langle h\rangle\), and \(\langle vh\rangle\). The reason for this is that none of these groups are subgroups of each other.

The next two theorems provide some further insight into the overall structure of subgroups of a group.

Theorem \(\PageIndex{2}\): Subgroup Intersection

If \(G\) is a group such that \(H,K\leq G\), then \(H\cap K\leq G\). Moreover, \(H\cap K\) is the largest subgroup contained in both \(H\) and \(K\).

Figure \(\PageIndex{2}\): Subgroup Lattice for \(V_4\)

It turns out that we cannot simply replace “intersection" with “union" in the previous theorem.

Problem \(\PageIndex{1}\)

Provide an example of a group \(G\) and subgroups \(H\) and \(K\) such that \(H\cup K\) is not a subgroup of \(G\).

Theorem \(\PageIndex{3}\): Subgroup Generated Union

If \(G\) is a group such that \(H,K\leq G\), then \(\langle H\cup K\rangle\leq G\). Moreover, \(\langle H\cup K\rangle\leq G\) is the smallest subgroup containing both \(H\) and \(K\).

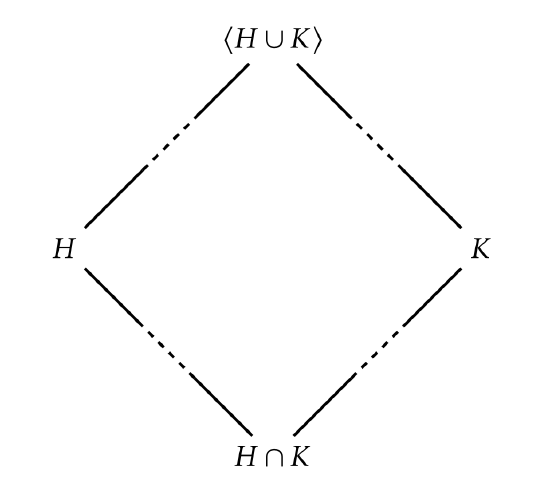
Theorems \(\PageIndex{2}\) and \(\PageIndex{3}\) justify the use of the word “lattice" in “subgroup lattice". In general, a lattice is a partially ordered set in which every two elements have a unique meet (also called a greatest lower bound or infimum) and a unique join (also called a least upper bound or supremum). In the case of a subgroup lattice for a group \(G\), the meet of subgroups \(H\) and \(K\) is \(H\cap K\) and the join is \(\langle H\cup K\rangle\). Figure \(\PageIndex{3}\) illustrates the meet (Theorem \(\PageIndex{2}\)) and join (Theorem \(\PageIndex{3}\)) in the case when \(H\) and \(K\) are not comparable.

Figure \(\PageIndex{3}\): Meet and join for subgroups \(H\) and \(K\)

In the next few problems, you are asked to create subgroup lattices. As you do this, try to minimize the amount of work it takes to come up with all the subgroups.

Problem \(\PageIndex{2}\)

Find all the subgroups of \(R_5=\{e,r,r^2,r^3,r^4\}\) (where \(r\) is clockwise rotation of a regular pentagon by \(72^{\circ}\)) and then draw the subgroup lattice for \(R_5\).

Problem \(\PageIndex{3}\)

Find all the subgroups of \(R_6=\{e,r,r^2,r^3,r^4,r^5\}\) (where \(r\) is clockwise rotation of a regular hexagon by \(60^{\circ}\)) and then draw the subgroup lattice for \(R_6\).

Problem \(\PageIndex{4}\): Lattice \(D_3\)

Find all the subgroups of \(D_3=\{e,r,r^2,s,sr,sr^2\}\) (where \(r\) and \(s\) are the usual symmetries of an equilateral triangle) and then draw the subgroup lattice for \(D_3\).

Problem \(\PageIndex{5}\)

Find all the subgroups of \(S_3=\langle s_1, s_2\rangle\) (where \(s_1\) is the action that swaps the positions of the first and second coins and \(s_2\) is the action that swaps the second and third coins; see Problem 2.4.5) and then draw the subgroup lattice for \(S_3\). How does your lattice compare to the one in Problem \(\PageIndex{4}\)? You should look back at parts (e) and (f) of Problem 2.6.5 and ponder what just happened.

Problem \(\PageIndex{6}\)

Find all the subgroups of \(D_4=\{e,r,r^2,r^3,s,sr,sr^2,sr^3\}\) (where \(r\) and \(s\) are the usual symmetries of a square) and then draw the subgroup lattice for \(D_4\).

Problem \(\PageIndex{7}\)

Find all the subgroups of \(Q_8=\{1,-1,i,-i,j,-j,k,-k\}\) and then draw the subgroup lattice for \(Q_8\).