5.2: Lagrange's Theorem
- Page ID
- 98001
We’re finally ready to state Lagrange’s Theorem, which is named after the Italian born mathematician Joseph Louis Lagrange. It turns out that Lagrange did not actually prove the theorem that is named after him. The theorem was actually proved by Carl Friedrich Gauss in 1801.
Let \(G\) be a finite group and let \(H\leq G\). Then \(|H|\) divides \(|G|\).
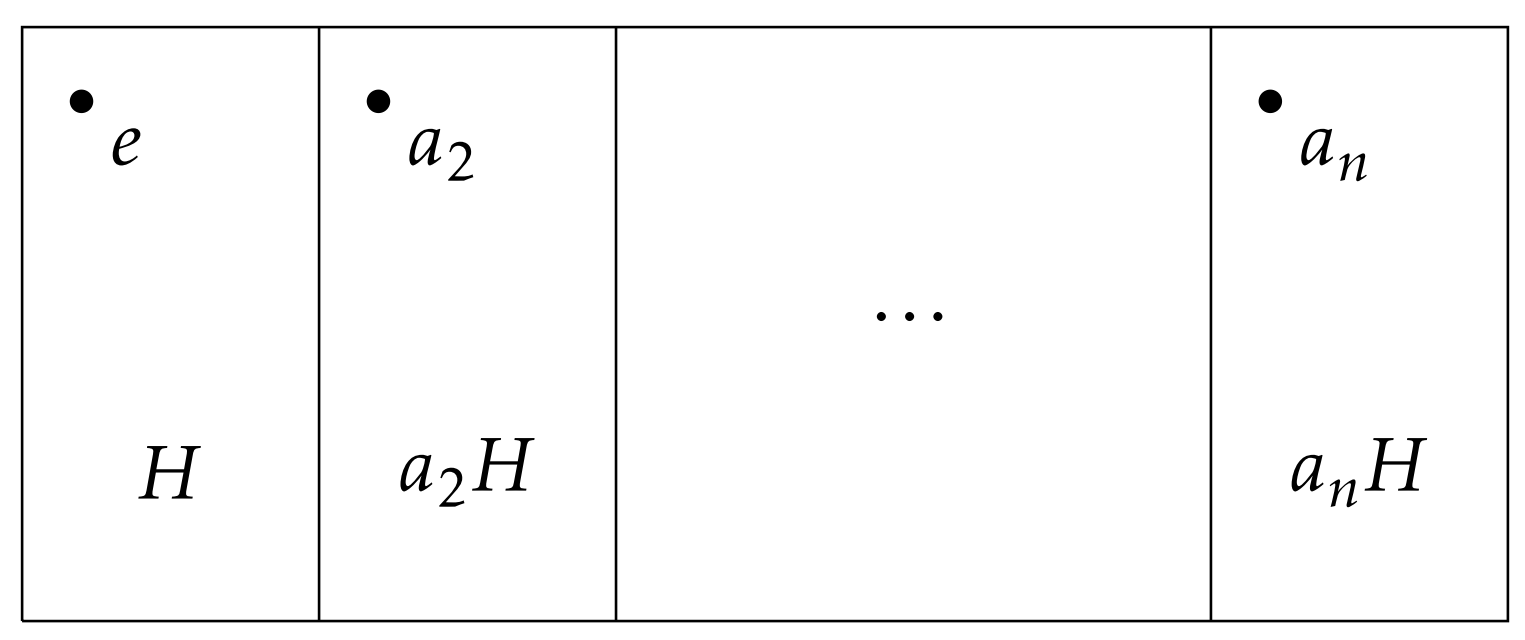
This simple sounding theorem is extremely powerful. One consequence is that groups and subgroups have a fairly rigid structure. Suppose \(G\) is a finite group and let \(H\leq G\). Since \(G\) is finite, there must be a finite number of distinct left cosets, say \(H, a_2H, \ldots, a_{n}H\). Corollary 5.1.2 tells us that each of these cosets is the same size. In particular, Lagrange’s Theorem implies that for each \(i\in\{1,\ldots, n\}\), \(|a_iH|=|G|/n\), or equivalently \(n=|G|/|a_iH|\). This is depicted in Figure \(\PageIndex{1}\), where each rectangle represents a coset and we’ve labeled a single coset representative in each case.
One important consequence of Lagrange’s Theorem is that it narrows down the possible sizes for subgroups.
Suppose \(G\) is a group of order 48. What are the possible orders for subgroups of \(G\)?
Lagrange’s Theorem tells us what the possible orders of a subgroup are, but if \(k\) is a divisor of the order of a group, it does not guarantee that there is a subgroup of order \(k\). It’s not too hard to show that the converse of Lagrange’s Theorem is true for cyclic groups. However, it’s not true, in general.
Provide an example of a finite group \(G\) such that \(|G|\) has a divisor \(k\) but \(G\) does not have a subgroup of order \(k\).
Using Lagrange’s Theorem, we can quickly prove both of the following theorems.
Let \(G\) be a finite group and let \(a\in G\). Then \(|a|\) divides \(|G|\).
The next exercise shows us that the converse of Theorem \(\PageIndex{2}\) is not true.
Argue that \(S_4\) does not have any elements of order 8.
For every prime \(p\), if \(G\) has order \(p\), then \(G\cong \mathbb{Z}_p\).
For every prime \(p\), there is a unique group of order \(p\) up to isomorphism.
Lagrange’s Theorem motivates the following definition.
Let \(G\) be a group and let \(H\leq G\). The index of \(H\) in \(G\) is the number of cosets (left or right) of \(H\) in \(G\). Equivalently, if \(G\) is finite, then the index of \(H\) in \(G\) is equal to \(|G|/|H|\). We denote the index via \([G:H]\).
Let \(H=\langle (1,2)(3,4),(1,3)(2,4)\rangle\).
- Find \([A_4:H]\).
- Find \([S_4:H]\).
Find \([\mathbb{Z}:4\mathbb{Z}]\).