6.1: Products of Groups

In this section, we will discuss a method for using existing groups as building blocks to form new groups.

Suppose \((G,*)\) and \((H,\odot)\) are two groups. Recall that the Cartesian product of \(G\) and \(H\) is defined to be \[G\times H=\{(g,h)\mid g\in G,h\in H\}\] Using the binary operations for the groups \(G\) and \(H\), we can define a binary operation on the set \(G\times H\). Define \(\star\) on \(G\times H\) via \[(g_1,h_1)\star(g_2,h_2)=(g_1*g_2,h_1\odot h_2).\] This looks fancier than it is. We’re just doing the operation of each group in the appropriate component. It turns out that \((G\times H,\star)\) is a group.

Theorem \(\PageIndex{1}\)

Suppose \((G,*)\) and \((H,\odot)\) are two groups, where \(e\) and \(e'\) are the identity elements of \(G\) and \(H\), respectively. Then \((G\times H,\star)\) is a group, where \(\star\) is defined as above. Moreover, \((e,e')\) is the identity of \(G\times H\) and the inverse of \((g,h)\in G\times H\) is given by \((g,h)^{-1}=(g^{-1},h^{-1})\).

We refer to \(G\times H\) as the direct product of the groups \(G\) and \(H\). In this case, each of \(G\) and \(H\) is called a factor of the direct product. We often abbreviate \((g_1,h_1)\star(g_2,h_2)=(g_1*g_2,h_1\odot h_2)\) by \((g_1,h_1)(g_2,h_2)=(g_1 g_2,h_1 h_2)\). One exception to this is if we are using the operation of addition in each component. For example, consider \(\mathbb{Z}_4\times \mathbb{Z}_2\) under the operation of addition mod 4 in the first component and addition mod 2 in the second component. Then \[\mathbb{Z}_4 \times \mathbb{Z}_2=\{(0,0),(1,0),(2,0),(3,0),(0,1),(1,1),(2,1),(3,1)\}.\] In this case, we will use additive notation in \(\mathbb{Z}_4\times \mathbb{Z}_2\). For example, in \(\mathbb{Z}_4 \times \mathbb{Z}_2\) we have \[(2,1)+(3,1)=(1,0)\] and \[(1,0)+(2,1)=(3,1).\] Moreover, the identity of the group is \((0,0)\). As an example, the inverse of \((1,1)\) is \((3,1)\) since \((1,1)+(3,1)=(0,0)\). There is a very natural generating set for \(\mathbb{Z}_4\times \mathbb{Z}_2\), namely, \(\{(1,0),(0,1)\}\) since \(1\in \mathbb{Z}_4\) and \(1\in \mathbb{Z}_2\) generate \(\mathbb{Z}_4\) and \(\mathbb{Z}_2\), respectively. The corresponding Cayley diagram is given in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Cayley diagram for \(\mathbb{Z}_4 \times \mathbb{Z}_2\) with generating set \(\{(1, 0),(0, 1)\}\).

Problem \(\PageIndex{1}\)

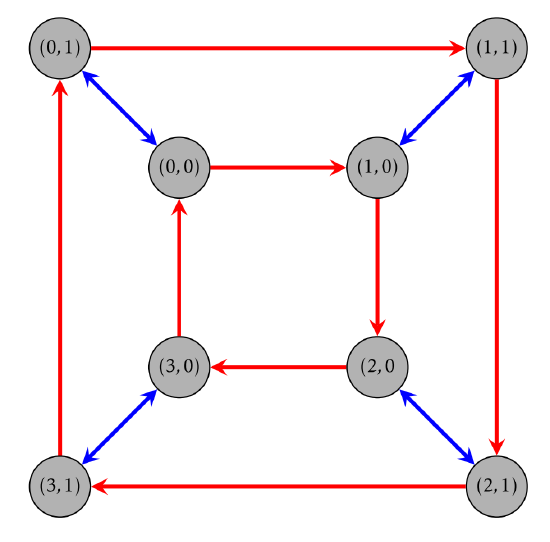
Consider the group \(\mathbb{Z}_4 \times \mathbb{Z}_2\). Is this group abelian? Is the group cyclic? Determine whether \(\mathbb{Z}_4 \times \mathbb{Z}_2\) is isomorphic to any of \(D_4\), \(Q_8\), \(\mathbb{Z}_8\), or \(L_3\).

The upshot of the previous problem is that there are at least five groups of order 8 up to isomorphism. It turns out that there are exactly five groups of order 8 up to isomorphism. In particular, every group of order 8 is isomorphic to one of the following groups: \(\mathbb{Z}_8\), \(\mathbb{Z}_4 \times \mathbb{Z}_2\), \(L_3\), \(D_4\), and \(Q_8\). Note that \(R_8\cong \mathbb{Z}_8\) and \(\text{Spin}_{1\times 2}\cong D_4\). Three of the isomorphism classes correspond to abelian groups while the other two correspond to non-abelian groups. Unfortunately, we will not develop the tools necessary to prove that this classification is complete.

The next two theorems should not be terribly surprising.

Theorem \(\PageIndex{2}\)

If \(G_1\) and \(G_2\) are groups, then \(G_1\times G_2\cong G_2\times G_1\).

Theorem \(\PageIndex{3}\)

Suppose \(G_1\) and \(G_2\) are groups with identities \(e_1\) and \(e_2\), respectively. Then \(\{e_1\}\times G_2\cong G_2\) and \(G_1\times \{e_2\}\cong G_1\).

There’s no reason we can’t take the direct product of more than two groups. If \(A_1, A_2, \ldots, A_n\) is a collection of sets, we define \[\prod_{i=1}^nA_i:=A_1\times A_2\times \cdots \times A_n.\] Each element of \(\prod_{i=1}^nA_i\) is of the form \((a_1,a_2,\ldots, a_n)\), where \(a_i\in A_i\).

Theorem \(\PageIndex{4}\)

Let \(G_1, G_2,\ldots, G_n\) be groups. For \((a_1,a_2, \ldots, a_n), (b_1,b_2,\ldots, b_n)\in \prod_{i=1}^nG_i\), define \[(a_1,a_2, \ldots, a_n)(b_1,b_2,\ldots, b_n)=(a_1b_1,a_2b_2,\ldots, a_nb_n).\] Then \(\prod_{i=1}^nG_i\), the direct product of \(G_1,\ldots, G_n\), is a group under this binary operation.

One way to think about direct products is that we can navigate the product by navigating each factor simultaneously but independently. Computing the order of a group that is a direct product is straightforward.

Theorem \(\PageIndex{5}\)

Let \(G_1, G_2,\ldots, G_n\) be finite groups. Then \[|G_1\times G_2\times \cdots \times G_n|=|G_1|\cdot|G_2|\cdots |G_n|.\]

Theorem \(\PageIndex{6}\)

Let \(G_1, G_2,\ldots, G_n\) be groups. Then \(|G_1\times G_2\times \cdots \times G_n|\) is infinite if and only if at least one \(|G_i|\) is infinite.

The following theorem should be clear.

Theorem \(\PageIndex{7}\): Product Adelian Groups

Let \(G_1, G_2,\ldots, G_n\) be groups. Then \(\prod_{i=1}^nG_i\) is abelian if and only if each \(G_i\) is abelian.

Let’s play with a few more examples.

Problem \(\PageIndex{2}\)

Draw the Cayley diagram for \(\mathbb{Z}_2\times \mathbb{Z}_3\) using \(\{(1,0),(0,1)\}\) as the generating set. Is \(\mathbb{Z}_2\times \mathbb{Z}_3\) an abelian group? Is it cyclic? What familiar group is \(\mathbb{Z}_2\times \mathbb{Z}_3\) isomorphic to?

Problem \(\PageIndex{3}\)

Consider \(\mathbb{Z}_2\times \mathbb{Z}_2\) under the operation of addition mod 2 in each component. Find a generating set for \(\mathbb{Z}_2\times \mathbb{Z}_2\) and then create a Cayley diagram for this group. What well-known group is \(\mathbb{Z}_2\times \mathbb{Z}_2\) isomorphic to?

Consider the similarities and differences between \(\mathbb{Z}_2\times \mathbb{Z}_3\) and \(\mathbb{Z}_2\times \mathbb{Z}_2\). Both groups are abelian by Theorem \(\PageIndex{7}\), but only the former is cyclic. Here’s another exercise.

Problem \(\PageIndex{4}\)

Consider the group \(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\). Find a generating set for \(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\) and then create a Cayley diagram for this group. Is there a group that we have seen before that \(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\) isomorphic to?

The next theorem tells us how to compute the order of an element in a direct product of groups.

Theorem \(\PageIndex{8}\)

Suppose \(G_1, G_2,\ldots, G_n\) are groups and let \((g_1,g_2,\ldots, g_n)\in \prod_{i=1}^nG_i\). If \(|g_i|=r_i<\infty\), then \(|(g_1,g_2,\ldots, g_n)|=\text{lcm}(r_1,r_2,\ldots,r_n)\).

Problem \(\PageIndex{5}\)

Find the order of each of the following elements.

1. \((6,5)\in\mathbb{Z}_{12}\times \mathbb{Z}_7\).
2. \((r,i)\in D_3\times Q_8\).
3. \(((1,2)(3,4),3)\in S_4\times \mathbb{Z}_{15}\).

Problem \(\PageIndex{6}\)

Find the largest possible order of elements in each of the following groups.

1. \(\mathbb{Z}_6\times \mathbb{Z}_8\)
2. \(\mathbb{Z}_9\times \mathbb{Z}_{12}\)
3. \(\mathbb{Z}_4\times \mathbb{Z}_{18}\times \mathbb{Z}_{15}\)

Theorem \(\PageIndex{9}\)

The group \(\mathbb{Z}_m\times \mathbb{Z}_n\) is cyclic if and only if \(m\) and \(n\) are relatively prime.

Corollary \(\PageIndex{1}\)

The group \(\mathbb{Z}_m\times \mathbb{Z}_n\) is isomorphic to \(\mathbb{Z}_{mn}\) if and only if \(m\) and \(n\) are relatively prime.

The previous results can be extended to more than two factors.

Theorem \(\PageIndex{10}\)

The group \(\prod_{i=1}^n \mathbb{Z}_{m_i}\) is cyclic and isomorphic to \(\mathbb{Z}_{m_1m_2\cdots m_n}\) if and only if every pair from the collection \(\{m_1,m_2,\ldots, m_n\}\) is relatively prime.

Problem \(\PageIndex{7}\)

Determine whether each of the following groups is cyclic.

1. \(\mathbb{Z}_7\times \mathbb{Z}_8\)
2. \(\mathbb{Z}_7\times \mathbb{Z}_7\)
3. \(\mathbb{Z}_2\times \mathbb{Z}_7\times \mathbb{Z}_8\)
4. \(\mathbb{Z}_5\times \mathbb{Z}_7\times \mathbb{Z}_8\)

Theorem \(\PageIndex{11}\)

Suppose \(n=p_1^{n_1}p_2^{n_2}\cdots p_r^{n_r}\), where each \(p_i\) is a distinct prime number. Then \[\mathbb{Z}_n\cong \mathbb{Z}_{p_1^{n_1}}\times \mathbb{Z}_{p_2^{n_2}}\times \cdots \times \mathbb{Z}_{p_r^{n_r}}.\]

The next theorem tells us that the direct product of subgroups is always a subgroup.

Theorem \(\PageIndex{12}\): Product of Subgroups

Suppose \(G_1\) and \(G_2\) are groups such that \(H_1\leq G_1\) and \(H_2\leq G_2\). Then \(H_1\times H_2\leq G_1\times G_2\).

However, not every subgroup of a direct product has the form above.

Problem \(\PageIndex{8}\)

Find an example that illustrates that not every subgroup of a direct product is the direct product of subgroups of the factors.

Problem \(\PageIndex{9}\)

Can we extend Theorem \(\PageIndex{12}\) to normal subgroups? That is, if \(H_1\trianglelefteq G_1\) and \(H_2\trianglelefteq G_2\), is it the case that \(H_1\times H_2\trianglelefteq G_1\times G_2\)? If so, prove it. Otherwise, provide a counterexample.

The next theorem describes precisely the structure of finite abelian groups. We will omit its proof, but allow ourselves to utilize it as needed.

Theorem \(\PageIndex{13}\): Fundamental Theorem of Finitely Generated Abelian Groups

Every finitely generated abelian group \(G\) is isomorphic to a direct product of cyclic groups of the form \[\mathbb{Z}_{p_1^{n_1}}\times \mathbb{Z}_{p_2^{n_2}}\times \cdots \times \mathbb{Z}_{p_r^{n_r}}\times \mathbb{Z}^k,\] where each \(p_i\) is a prime number (not necessarily distinct). The product is unique up to rearrangement of the factors.

Note that the number \(k\) is called the Betti number. A finitely generated abelian group is finite if and only if the Betti number is 0.

Problem \(\PageIndex{10}\): Groups Order 8

Find all abelian groups up to isomorphism of order 8. How many different groups up to isomorphism (both abelian and non-abelian) have we seen and what are they?

Problem \(\PageIndex{11}\)

Find all abelian groups up to isomorphism for each of the following orders.

1. 16
2. 12
3. 25
4. 30
5. 60