6.2: Quotients of Groups

In the previous section, we discussed a method for constructing “larger" groups from “smaller" groups using a direct product construction. In this section, we will in some sense do the opposite.

Problem 5.3.2 hinted that if \(H\leq G\) and we arrange the group table according to the left cosets of \(H\), then the group table will have checkerboard pattern if and only if \(H\) is normal in G (i.e., the left and right cosets of \(H\) are the same). For example, see the colored table prior to Problem 5.1.2 versus the ones you created in Exercises 5.1.2, 5.1.3. If we have the checkerboard pattern in the group table that arises from a normal subgroup, then by “gluing together" the colored blocks, we obtain a group table for a smaller group that has the cosets as the elements.

For example, let’s consider \(K=\langle -1\rangle \leq Q_8\). Problem 5.1.3 showed us that \(K\) is normal \(Q_8\). The left (and right) cosets of \(K\) in \(Q_8\) are \[K=\{1,-1\}, iK=\{i,-i\}, jK=\{j,-j\}, \text{ and } kK=\{k,-k\}.\] As you found in Problem 5.1.3, if we arrange the rows and columns of \(Q_8\) according to these cosets, we obtain the following group table.

Figure \(\PageIndex{1}\)

If we consider the \(2\times 2\) blocks as elements, it appears that we have a group table for a group with 4 elements. Closer inspection reveals that this looks like the table for \(V_4\). If the table of \(2\times 2\) blocks is going to represent a group, we need to understand the binary operation. How do we “multiply" cosets? For example, the table suggests that the coset \(jK\) (colored in red) times the coset \(iK\) (colored in blue) is equal to \(kK\) (colored in purple) despite the fact that \(ji=-k\neq k\). Yet, it is true that the product \(ji=-k\) is an element in the coset \(kK\). In fact, if we look closely at the table, we see that if we pick any two cosets, the product of any element of the first coset times any element of the second coset will always result in an element in the same coset regardless of which representatives we chose.

In other words, it looks like we can multiply cosets by choosing any representative from each coset and then seeing what coset the product of the representatives lies in. However, it is important to point out that this will only work if we have a checkerboard pattern of cosets, which we have seen evidence of only happening when the corresponding subgroup is normal.

Before continuing, let’s continue tinkering with the same example. Consider the Cayley diagram for \(Q_8\) with generators \(\{i,j,-1\}\) that is given in Figure \(\PageIndex{2}\)a.

Figure \(\PageIndex{2}\): The left subfigure shows the Cayley diagram for \(Q_8\) with generating set \(\{i,j,-1\}\). The right subfigure shows the collapsed Cayley diagram for \(Q_8\) according to the left cosets of \(K=\langle -1\rangle\).

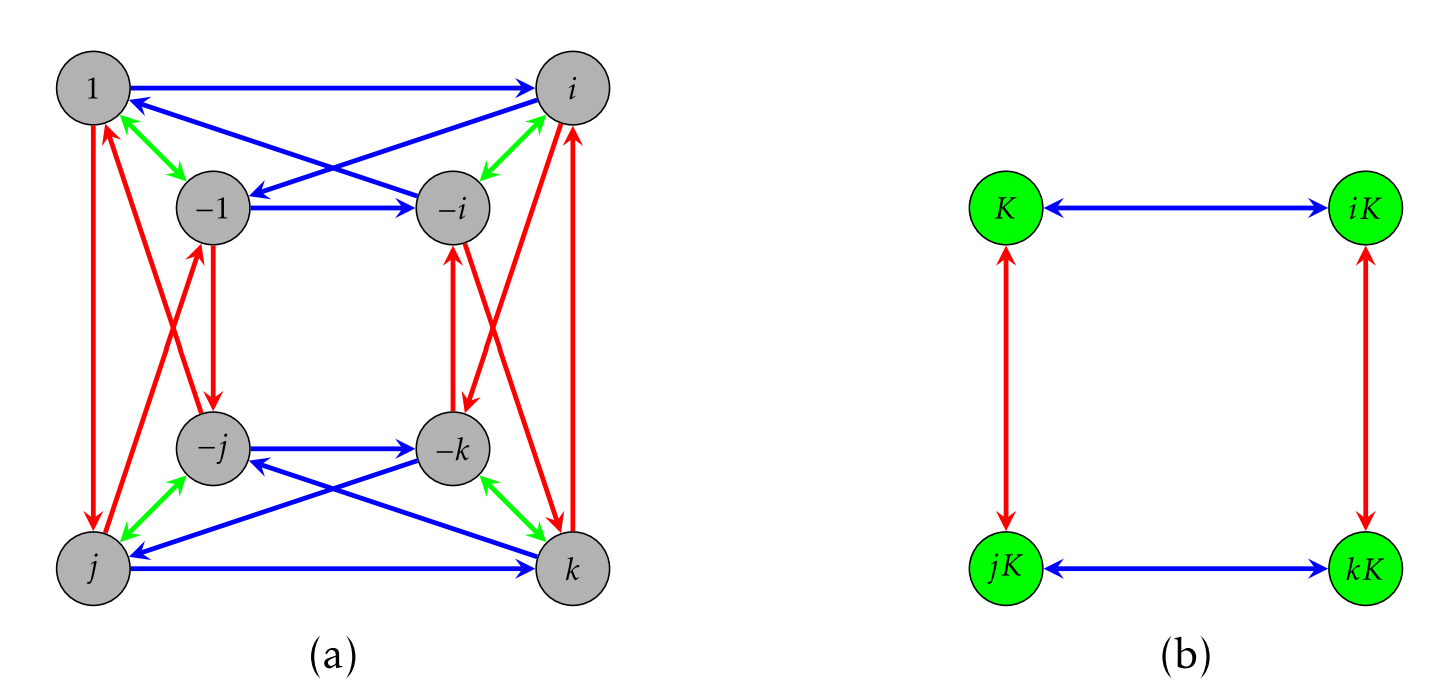
We can visualize the right cosets of \(K\) as the clumps of vertices connected together with the two-way green arrows. In this case, we are also seeing the left cosets since \(K\) is normal in \(Q_8\). If we collapse the cosets onto each other and collapse the corresponding arrows, we obtain the diagram given in Figure \(\PageIndex{2}\)(b). It is clear that this diagram is the Cayley diagram for a group that is isomorphic to \(V_4\). For reasons we will understand shortly, this processing of collapsing a Cayley diagram according to the cosets of a normal subgroup is called the “quotient process."

Problem \(\PageIndex{1}\): Bad Quotient

Let’s see what happens if we attempt the quotient process for a subgroup that is not normal. Consider \(H=\langle s\rangle \leq D_3\). In Problem 5.1.1, we discovered that the left cosets of \(H\) are not the same as the right cosets of \(H\). This implies that \(H\) is not normal in \(D_3\). Consider the standard Cayley diagram for \(D_3\) that uses the generators \(r\) and \(s\). Draw the diagram that results from attempting the quotient process on \(D_3\) using the subgroup \(H\). Explain why this diagram cannot be the diagram for a group.

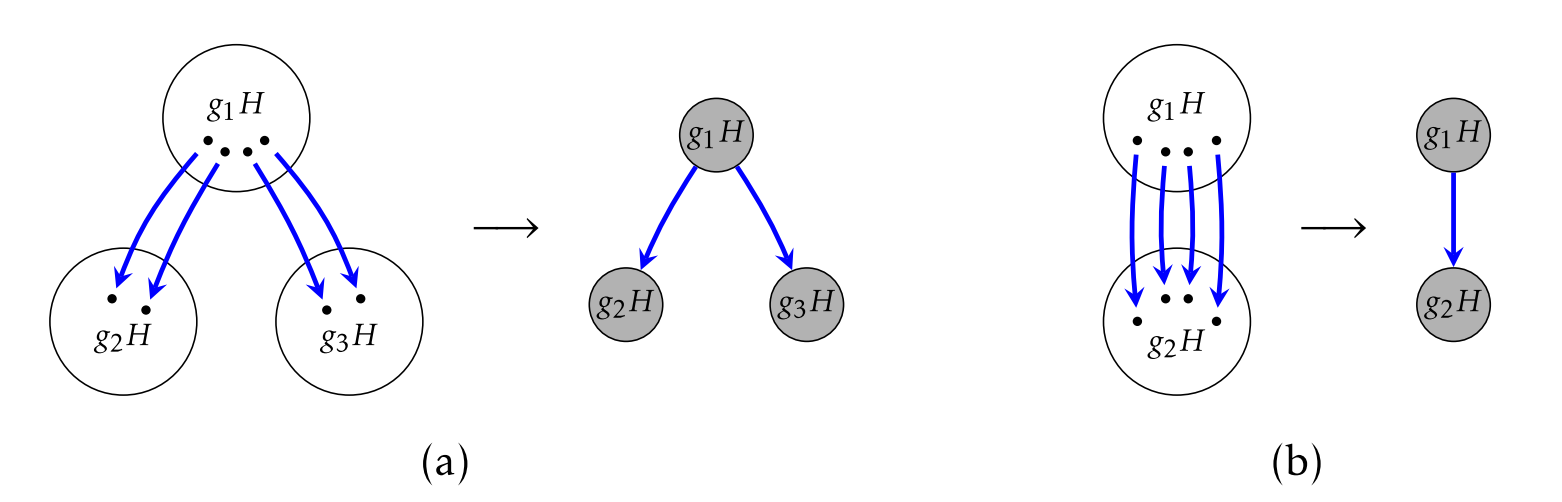
The problem that arises in Problem \(\PageIndex{1}\) is that if the same arrow types (i.e., those representing the same generator) leaving a coset do not point at elements in the same coset, attempting the quotient process will result in a diagram that cannot be a Cayley diagram for a group since we have more than one arrow of the same type leaving a vertex. In Figure \(\PageIndex{3}\)a, we illustrate what goes wrong if all the arrows for a generator pointing out of a coset do not unanimously point to elements in the same coset. In Figure \(\PageIndex{3}\)b, all the arrows point to elements in the same coset, and in this case, it appears that everything works out just fine.

Figure \(\PageIndex{3}\): In the left subfigure, blue arrows go from elements of the left coset \(g_1H\) to elements of multiple left cosets, which results in ambiguous blue arrows in the collapsed diagram. This implies that left coset multiplication is not well-defined in this case. In the right subfigure, blue arrows go from elements of the left coset \(g_1H\) to elements inside a unique left coset, which does not result in any ambiguity.

Problem \(\PageIndex{2}\)

In Problem 5.1.2, we learned that the subgroup \(K=\langle r\rangle\) is normal in \(D_3\) since the left cosets are equal to the right cosets. Note that this follows immediately from Theorem 5.3.3 since \([D_3:K]=2\). Draw the diagram that results from performing the quotient process to \(D_3\) using the subgroup \(K\). Does the resulting diagram represent a group? If so, what group is it isomorphic to?

Now, suppose \(G\) is an arbitrary group and let \(H\leq G\). Consider the set of left cosets of \(H\). We define \[(aH)(bH):=(ab)H.\] The natural question to ask is whether this operation is well-defined. That is, does the result of multiplying two left cosets depend on our choice of representatives? More specifically, suppose \(c\in aH\) and \(d\in bH\). Then \(cH=aH\) and \(dH=bH\). According to the operation defined above, \((cH)(dH)=cdH\). It better be the case that \(cdH=abH\), otherwise the operation is not well-defined.

Problem \(\PageIndex{3}\)

Let \(H=\langle s\rangle \leq D_3\). Find specific examples of \(a,b,c,d\in D_3\) such that \[(aH)(bH)\neq (cH)(dH)\] even though \(aH=cH\) and \(bH=dH\).

Theorem \(\PageIndex{1}\)

Let \(G\) be a group and let \(H\leq G\). Then left coset multiplication (as defined above) is well-defined if and only if \(H\trianglelefteq G\).

Theorem \(\PageIndex{2}\):Quotient Group

Let \(G\) be a group and let \(H\trianglelefteq G\). Then the set of left cosets of \(H\) in \(G\) forms a group under left coset multiplication.

The group from Theorem \(\PageIndex{2}\) is denoted by \(G/H\), read “\(G\) mod \(H\)", and is referred to as the quotient group (or factor group) of \(G\) by \(H\). If \(G\) is a finite group, then \(G/H\) is exactly the group that arises from “gluing together" the colored blocks in a checkerboard-patterned group table. It’s also the group that we get after applying the quotient process to the Cayley diagram. It’s important to point out once more that this only works properly if \(H\) is a normal subgroup.

Recall that Theorem [thm:AbelianImpliesNormal] tells us that if \(G\) is abelian, then every subgroup is normal. This implies that when \(G\) is abelian, \(G/H\) is a well-defined group for every subgroup \(H\) of \(G\). However, it is not necessary for \(G\) to be abelian in order for \(G/H\) to be a well-defined group. The quotient group \(Q_8/\langle -1\rangle\) is an example where this happens.

The next theorem tells us how to compute the order of a quotient group.

Theorem \(\PageIndex{3}\)

Let \(G\) be a group and let \(H\trianglelefteq G\). Then \(|G/H|=[G:H]\). In particular, if \(G\) is finite, then \(|G/H|=|G|/|H|\).

It’s important to point out that the order of a quotient group might be finite even if \(G\) has infinite order.

Problem \(\PageIndex{4}\)

Consider the group \((\mathbb{Z},+)\). Since \(\mathbb{Z}\) is abelian, every subgroup is normal. For example, \(4\mathbb{Z} \trianglelefteq \mathbb{Z}\), which implies that \(\mathbb{Z}/4\mathbb{Z}\) is a well-defined quotient group. Moreover, both \(\mathbb{Z}\) and \(4\mathbb{Z}\) have infinite order. What is \(|\mathbb{Z}/4\mathbb{Z}|\) equal to? Can you determine what well-known group \(\mathbb{Z}/4\mathbb{Z}\) is isomorphic to?

Suppose \(G\) is a group and \(H\trianglelefteq G\), so that \(G/H\) is a group. Recall that the elements of the group \(G/H\) are the left cosets of \(H\), which are of the form \(aH\) where \(a\in G\). The operation of the group is defined via \[(aH)(bH) = abH.\] Moreover, the identity in \(G/H\) is \(eH = H\) since \((aH)(eH) = aH\). By Corollary 4.1.2 \(|aH| = k\) if and only \((aH)^k = H\) and \(k\) is the smallest such positive exponent with this property. But notice that \((aH)^k = a^kH\). So, in order to compute the order of \(aH\), we need to find the smallest positive exponent \(k\) such that \(a^kH = H\), but \(a^kH = H\) exactly when \(a^k\) is in \(H\). The upshot is that to find the order of \(aH\) in \(G/H\), we need the smallest positive \(k\) such that \(a^k\) is in \(H\).

Problem \(\PageIndex{5}\)

Find the order of the given element in the quotient group. You may assume that we are taking the quotient by a normal subgroup.

1. \(s\langle r\rangle \in D_4/\langle r\rangle\)
2. \(j\langle -1\rangle \in Q_8/\langle -1\rangle\)
3. \(5+\langle 4\rangle \in \mathbb{Z}_{12}/\langle 4\rangle\)
4. \((2,1)+\langle (1,1)\rangle \in (\mathbb{Z}_3\times \mathbb{Z}_6)/\langle (1,1)\rangle\)
5. \((1,3)+\langle (0,2)\rangle\in (\mathbb{Z}_4\times \mathbb{Z}_8)/\langle (0,2)\rangle\)

Problem \(\PageIndex{6}\)

For each quotient group below, describe the group. If possible, state what group each is isomorphic to. You may assume that we are taking the quotient by a normal subgroup.

1. \(Q_8/\langle -1\rangle\)
2. \(Q_8/\langle i\rangle\)
3. \(\mathbb{Z}_4/\langle 2\rangle\)
4. \(V_4/\langle h\rangle\)
5. \(A_4/\langle (1,2)(3,4),(1,3)(2,4)\rangle\)
6. \((\mathbb{Z}_2\times \mathbb{Z}_2)/\langle (1,1)\rangle\)
7. \(\mathbb{Z}/4\mathbb{Z}\)
8. \(S_4/A_4\)
9. \((\mathbb{Z}_4\times \mathbb{Z}_2)/(\{0\}\times \mathbb{Z}_2)\)

Problem \(\PageIndex{7}\)

Compute the order of every element in the quotient group \((\mathbb{Z}_2\times \mathbb{Z}_4)/\langle (0,2)\rangle\). What well-known group is \((\mathbb{Z}_2\times \mathbb{Z}_4)/\langle (0,2)\rangle\) isomorphic to?

Theorem \(\PageIndex{4}\)

Let \(G\) be a group. Then

1. \(G/\{e\}\cong G\)
2. \(G/G\cong \{e\}\)

Theorem \(\PageIndex{5}\)

We have the following.

1. For \(n\geq 2\), \(S_n/A_n\cong \mathbb{Z}_2\).
2. For all \(n\in\mathbb{N}\), \(\mathbb{Z}/n\mathbb{Z}\cong \mathbb{Z}_n\).
3. For all \(n\in\mathbb{N}\), \(\mathbb{R}/n\mathbb{R}\cong \{e\}\).

Theorem \(\PageIndex{6}\)

Let \(G\) be a group and let \(H\trianglelefteq G\). If \(G\) is abelian, then so is \(G/H\).

Problem \(\PageIndex{8}\)

Show that the converse of the previous theorem is not true by providing a specific counterexample.

Problem \(\PageIndex{9}\)

Consider the quotient group \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\).

1. What is the order of \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\)?
2. Is the group abelian? Why?
3. Write down all the elements of \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\).
4. Does one of the elements generate the group?
5. What well-known group is \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\) isomorphic to?

Theorem \(\PageIndex{7}\)

Let \(G\) be a group and let \(H\trianglelefteq G\). If \(G\) is cyclic, then so is \(G/H\).

Problem \(\PageIndex{10}\)

Show that the converse of the previous theorem is not true by providing a specific counterexample.

Here are few additional exercises. These ones are a bit tougher.

Problem \(\PageIndex{11}\)

For each quotient group below, describe the group. If possible, state what group each is isomorphic to. You may assume that we are taking the quotient by a normal subgroup.

1. \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,2)\rangle\)
2. \((\mathbb{Z}\times \mathbb{Z})/\langle (1,1)\rangle\)
3. \(\mathbb{Q}/\langle 1\rangle\) (the operation on \(\mathbb{Q}\) is addition)