6.2: Orbits and Stabilizers
- Page ID
- 701
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we'll examine orbits and stabilizers, which will allow us to relate group actions to our previous study of cosets and quotients.
Let \(S\) be a \(G\)-set, and \(s\in S\). The orbit of \(s\) is the set \(G\cdot s = \{g\cdot s \mid g\in G\}\), the full set of objects that \(s\) is sent to under the action of \(G\).
There are a few questions that come up when encountering a new group action. The foremost is 'Given two elements \(s\) and \(t\) from the set \(S\), is there a group element such that \(g\cdot s=t\)?' In other words, can I use the group to get from any element of the set to any other? In the case of the action of \(S_n\) on a coin, the answer is yes. But in the case of \(S_4\) acting on the deck of cards, the answer is no. In fact, this is just a question about orbits. If there is only one orbit, then I can always find a group element to move from any object to any other object. This case has a special name.
A group action is transitive if \(G\cdot s = S\). In other words, for any \(s, t\in S\), there exists \(g\in G\) such that \(g\cdot s=t\). Equivalently, \(S\) contains a single orbit.
Equally important is the stabilizer of an element, the subset of \(G\) which leaves a given element \(s\) alone.
The stabilizer of \(s\) is the set \(G_s = \{g\in G \mid g\cdot s=s \}\), the set of elements of \(G\) which leave \(s\) unchanged under the action.
For example, the stabilizer of the coin with heads (or tails) up is \(A_n\), the set of permutations with positive sign. In our example with \(S_4\) acting on the small deck of eight cards, consider the card \(4D\). The stabilizer of \(4D\) is the set of permutations \(\sigma\) with \(\sigma(4)=4\); there are six such permutations.
In both of these examples, the stabilizer was a subgroup; this is a general fact!
| Proposition 6.1.3 |
|---|
| The stabilizer \(G_s\) of any element \(s \in S\) is a subgroup of \(G\). |
| Proof 6.1.4 |
|---|
| Let \(g, h \in G_s\). Then \(gh\cdot s = g\cdot (h\cdot s) = g\cdot s=s\). Thus, \(gh\in G_s\). If \(g\in G_s\), then so is \(g^{-1}\): By definition of a group action, \(1\in G_s\), so: Thus, \(G_s\) is a subgroup. |
Group action morphisms
And now some algebraic examples!
- Let \(G\) be any group and \(S=G\). The left regular action of \(G\) on itself is given by left multiplication: \(g\cdot h = gh\). The first condition for a group action holds by associativity of the group, and the second condition follows from the definition of the identity element. (There is also a right regular action, where \(g\cdot h = hg\); the action is 'on the right'.) The Cayley graph of the left regular action is the same as the usual Cayley graph of the group!
- Let \(H\) be a subgroup of \(G\), and let \(S\) be the set of cosets \(G/\mathord H\). The coset action is given by \(g\cdot (xH) = (gx)H\).
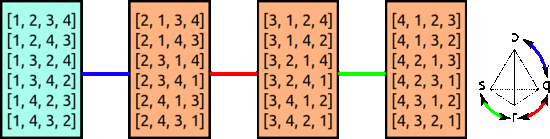
Figure 6.1: \(H\) is the subgroup of \(S_4\) with \(\sigma(1)=1\) for all \(\sigma\) in \(H\). This illustrates the action of \(S_4\) on cosets of \(H\).
- Show \(H_i\) is a subgroup of \(S_n\).
- Now let \(n=5\) and Sketch the Cayley graph of the coset action of \(S_5\) on \(H_1\) and \(H_3\).
| Proposition 6.1.6 |
|---|
| Let \(S\) be a \(G\)-set, with \(s\in S\) and \(G_s\). For any \(g, h\in G\), \(g\cdot s=h\cdot s\) if and only if \(gG_s=hG_s\). As a result, there is a bijection between elements of the orbit of \(s\) and cosets of the stabilizer \(G_s\). |
| Proof 6.1.7 |
|---|
| We have \(gG_s=hG_s\) if and only if \(h^{-1}g\in G_s\), if and only if \((h^{-1}g)\cdot s=s\), if and only if \(h\cdot s=g\cdot s\), as desired. |
In fact, we can generalize this idea considerably. We're actually identifying elements of the \(G\)-set with cosets of the stabilizer group, which is also a \(G\)-set; in other words, defining a function \(\phi\) between two \(G\)-sets. The theorem says that this function preserves the group operation: \(\phi(g\cdot s)=g\cdot \phi(s)\).
Let \(S, T\) be \(G\)-sets. A morphism of \(G\)-sets is a function \(\phi:S\rightarrow T\) such that \(\phi(g\cdot s)=g\cdot \phi(s)\) for all \(g\in G, s\in S\). We say the \(G\)-sets are isomorphic if \(\phi\) is a bijection.
We can then restate the proposition:
| Theorem 6.1.9 |
|---|
| For any \(s\) in a \(G\)-set \(S\), the orbit of \(S\) is isomorphic to the coset action on \(G_s\). |
Now we can use LaGrange's theorem in a very interesting way! We know that the cardinality of a subgroup divides the order of the group, and that the number of cosets of a subgroup \(H\) is equal to \(|G|/\mathord |H|\). Then we can use the relationship between cosets and orbits to observe the following:
| Theorem 6.1.10 |
|---|
| Let \(S\) be a \(G\)-set, with \(s\in S\). Then the size of the orbit of \(s\) is \(|G|/\mathord |G_s|\). |
For a somewhat obvious example, considering \(S_{13}\) acting on the numerical values of playing cards, we can observe that any given card is fixed by a subgroup of \(S_{13}\) isomorphic to \(S_{12}\) (switching around the other twelve numbers in any way doesn't change affect the given card). Then the size of the orbit of the card is \(|S_{13}|/\mathord |S_{12}| = 13\). That's a number we could have figured out directly by reasoning a bit, but it shows us that the theorem is working sensibly!
Now that we have a notion of isomorphism of \(G\)-sets, we can say something to classify \(G\)-sets. What kinds of actions are possible?
Let \(G\) be a finite group, and \(S\) a finite \(G\)-set. Then \(S\) is a collection of orbits. We knw that every orbit is isomorphic to \(G\) acting on the cosets of some subgroup of \(H\). So we have the following theorem:
| Theorem 6.1.11: Classification of \(G\)-Sets |
|---|
| Let \(G\) be a finite group, and \(S\) a finite \(G\)-set. Then \(S\) is isomorphic to a union of coset actions of \(G\) on subgroups. |
For example, \(S_{13}\) acting on a full deck of cards decomposes as a union of four orbits, each isomorphic to the coset action of \(S_{13}\) on a subgroup isomorphic to \(S_{12}\).
In short, to understand all possible \(G\)-sets, we should try to understand all of the subgroups of \(G\). In general, this is a hard problem, though it's easy for some cases.
- For \(n=15\), draw Cayley graphs of the coset action of \(\mathbb{Z}_{15}\) on each of it's cosets.
- Describe all the subgroups of \(\mathbb{Z}_n\) for arbitrary \(n\).
- Decompose the action of \(S_4\) on the subsets of \(\{1,2,3,4\}\) into orbits.
- Draw a Cayley graph of the action.
- Identify each orbit with the coset action on a subgroup of \(S_4\).
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


