2.1: Examples of groups

Groups are one of the most basic algebraic objects, yet have structure rich enough to be widely useful in all branches of mathematics and its applications. A group is a set \(G\) with a binary operation \(G\times G \to G\) that has a short list of specific properties. Before we give the complete definition of a group in the next section (see Definition 2.2.1), this section introduces examples of some important and useful groups.

Permutations

A permutation of a set \(X\) is a bijection from \(X\) to itself, that is, a function that is both one-to-one and onto. Given two permutations \(\alpha,\beta\) of a set \(X\text{,}\) we write \(\alpha\beta\) to denote the composition of functions \(\alpha\circ\beta\text{.}\)

Definition 2.1.1.

Let \(X\) be a set and let ⁡\(Perm(X)\) denote the set of all permutations of \(X\text{.}\) The group of permutations of \(X\) is the set \(G=Perm(X)\) together with the binary operation \(G\times G\to G\) given by function composition, that is, \((\alpha,\beta) \to \alpha\circ\beta\text{.}\) For the special case \(X = \{1,2,\ldots,n\}\) for some integer \(n\geq 1\text{,}\) the group \(Perm(X)\) is called the symmetric group, and is denoted \(S_n\text{.}\)

Checkpoint 2.1.2.

A permutation σ of \(X=\{1,2,\ldots,n\}\) can be specified by a list of values \([\sigma(1),\sigma(2),\ldots,\sigma(n)]\text{.}\)¹ For example, the list \([3,1,2]\) specifies the permutation \(\sigma\colon \{1,2,3\}\to\{1,2,3\}\) given by

\[
\sigma(1)=3, \; \sigma(2)=1,\; \sigma(3)=2.
\nonumber \]

Let \(\tau=[2,1,3]\text{.}\) Find \(\sigma\tau\text{,}\) \(\tau\sigma\text{,}\) and \(\sigma^2=\sigma\sigma\text{.}\)

Answer

\(\sigma\tau= [1,3,2]\text{,}\) \(\tau\sigma=[3,2,1]\text{,}\) \(\sigma^2=[2,3,1]\)

Symmetries of regular polygons

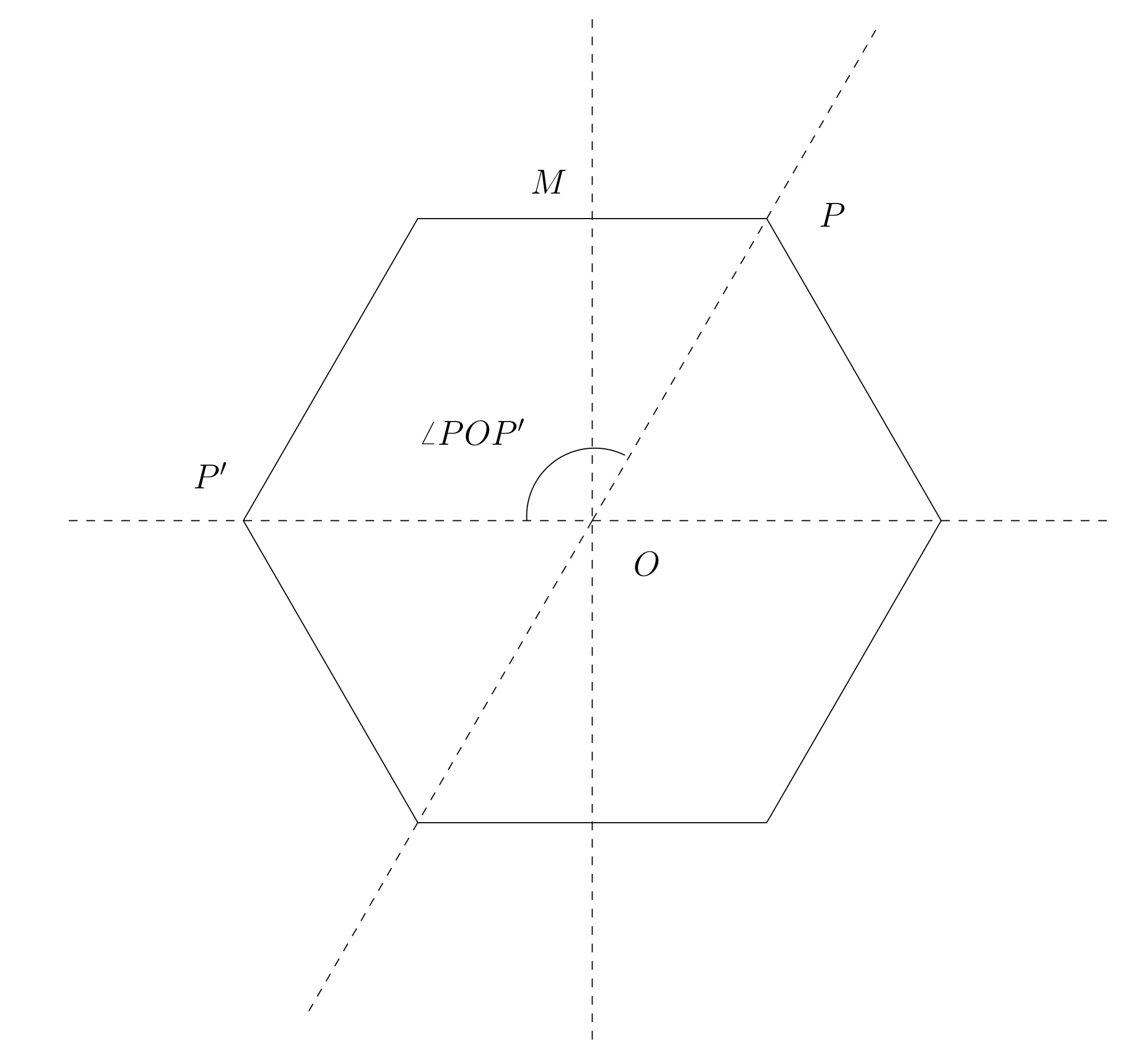
Informally and intuitively, we say that regular polygons have rotational and mirror symmetries. Specifically, the rotational symmetries are rotations about the center \(O\) of the polygon, clockwise or counterclockwise, by some angle \(\angle POP'\text{,}\) where \(P,P'\) are any two vertices. The mirror symmetries of the polygon are reflections across lines of the form \(\overline{OP}\) or \(\overline{OM}\text{,}\) where \(P\) is any vertex and \(M\) is the midpoint of any edge of the polygon. See Figure 2.1.3.

Figure 2.1.3. Symmetries of a regular \(n\)-gon

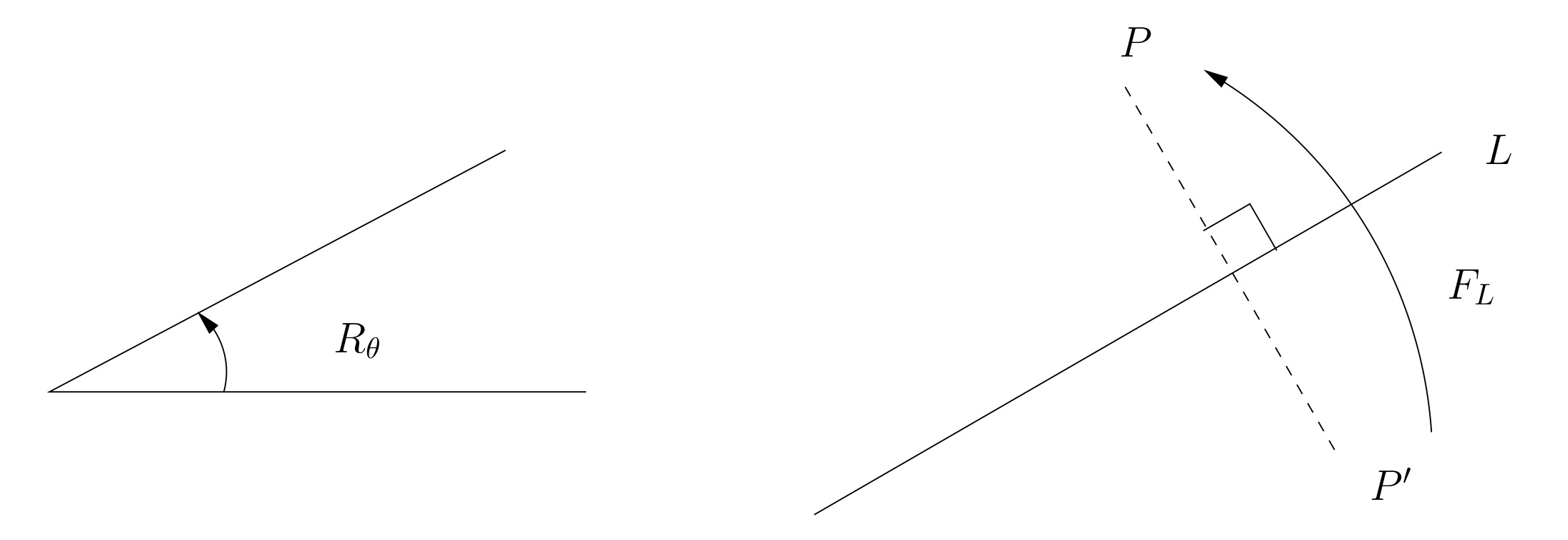
Here are some standard notations for rotations and reflections in the plane. See Figure 2.1.4.

Figure 2.1.4. Rotations and reflections in the plane

Rotations in the plane.

Fix a center point \(O\text{.}\) We write \(R_\theta\) to denote the rotation by angle \(\theta\) about the point \(O\text{.}\) Angle units can be revolutions or degrees or radians, whatever is most convenient. We observe the usual convention that positive values of \(\theta\) denote counterclockwise rotations and negative values of \(\theta\) denote clockwise rotations.

Reflections in the plane.

We write \(F_L\) to denote the reflection across the line \(L\text{.}\) This means that \(P'=F_L(P)\) if and only if \(\overline{PP'}\perp L\) and the distance from \(P\) to \(L\) is the same as the distance from \(P'\) to \(L\text{.}\)

Given symmetries \(A,B\text{,}\) we write \(AB\) to denote the composition \(A\circ B\text{.}\) For example, for the symmetries of the equilateral triangle, with angles in degrees, and with \(L=\overline{OP}\) for some vertex \(P\text{,}\) we have \(R_{240}R_{120}=R_{0}\) and \(F_LR_{120}=R_{-120}F_L\text{.}\)

Definition 2.1.5.

The dihedral group, denoted \(D_n\) is the set of rotation and reflection symmetries of the regular \(n\)-gon together with the binary operation of function composition.

Checkpoint 2.1.6.

Let \(X\) be the square centered at the origin in the \(x,y\)-plane with vertices at \((\pm 1,\pm 1)\text{.}\) The square \(X\) has lines of symmetry \(H,V,D,D'\) (horizontal, vertical, diagonal, and another diagonal) where \(H,V\) denote the \(x,y\) axes, respectively, and \(D,D'\) denote the lines \(y=-x,y=x\text{,}\) respectively. See Figure 2.1.7.

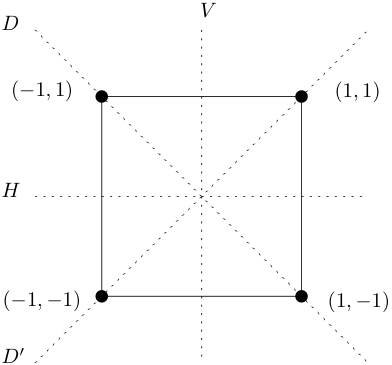
Figure 2.1.7. Lines of symmetry for the square.

The symmetries of the square \(X\) are

\[
D_4=\{R_0,R_{1/4},R_{1/2},R_{3/4},F_H,F_V,F_D,F_{D'}\}
\nonumber \]

where the rotation angles units are revolutions. Find the following.

1. \(\displaystyle R_{1/4}R_{1/2}\)
2. \(\displaystyle R_{1/4}F_H\)
3. \(\displaystyle F_HR_{1/4}\)
4. \(\displaystyle F_HF_D\)
5. \(\displaystyle F_DF_H\)
6. \(\displaystyle (F_DR_{1/2})^2= F_DR_{1/2}F_DR_{1/2}\)
7. \(\displaystyle (F_DR_{1/2})^3\)

Answer

1. \(\displaystyle R_{3/4}\)
2. \(\displaystyle F_{D'}\)
3. \(\displaystyle F_D\)
4. \(\displaystyle R_{1/4}\)
5. \(\displaystyle R_{3/4}\)
6. \(\displaystyle R_0\)
7. \(\displaystyle F_{D'}\)

The norm 1 complex numbers

Definition 2.1.8.

The circle group, denoted \(S^1\text{,}\) is the set

\[
S^1=\{z\in \mathbb{C}\colon |z|=1\}
\nonumber \]

of norm \(1\) complex numbers together with the binary operation \(S^1\times S^1\to S^2\) given by complex multiplication, that is, \((z,w)\to zw\text{.}\)

Checkpoint 2.1.9.

Show that if \(z,w\) are elements of \(S^1\text{,}\) then their product \(zw\) is also in \(S^1\text{.}\)

The n-th roots of unity

Let \(n\geq 1\) be an integer. The set

\[
C_n=\{z\in \mathbb{C}\colon
z^n=1\}
\nonumber \]

is called the set of (complex) \(n\)-th roots of unity.

Checkpoint 2.1.10.

1. Let \(\omega=e^{i2\pi/n}\text{.}\) Show that \(\omega^k\) is in \(C_n\) for all integers \(k\text{.}\)

2. Show that, if \(z\) is an element of \(C_n\text{,}\) then \(z=\omega^k\) for some integer \(k\text{.}\)

3. Show that the set \(C_n\) consists of precisely the \(n\) elements

\[
\{\omega^0,\omega^1,\omega^2,\ldots,\omega^{n-1}\}.
\nonumber \]

Definition 2.1.11.

The set \(C_n=\{\omega^0,\omega^1,\omega^2,\ldots,\omega^{n-1}\}\), together with the operation of complex multiplication, is called the group of \(n\)-th roots of unity.

Integers

Definition 2.1.12.

The set \(\mathbb{Z}\) of integers, together with the operation of addition, is called the group of integers. Similarly, the set \(\mathbb{Z}_n\) of integers modulo \(n\) (where \(n\) is some integer \(n\geq 1\)), together with the operation of addition modulo \(n\text{,}\) is called the group of integers mod \(n\).

Invertible matrices

Let \(n\geq 1\) be an integer. We write \(GL(n,\mathbb{R})\) to denote the set of \(n\times n\) invertible matrices with real entries. We write \(GL(n,\mathbb{C})\) to denote the set of \(n\times n\) invertible matrices with complex entries.

Definition 2.1.13.

The set \(GL(n,\mathbb{R})\) (respectively, \(GL(n,\mathbb{C})\), together with the binary operation of matrix multiplication, is called the group of \(n×n\) real (respectively, complex) invertible matrices, or also the general linear group

Nonzero elements in a field

Let \(\mathbb{F}\) be a field, such as the rational numbers \(\mathbb{Q}\), the real numbers \(\mathbb{R}\), or the complex numbers \(\mathbb{C}\). We write \(\mathbb{F}^\ast\) to denote the set of nonzero elements in \(\mathbb{F}\).

Definition 2.1.14.

Let \(\mathbb{F}\) be a field. The set \(\mathbb{F}^\ast\), together with the binary operation of multiplication, is called the group of nonzero elements in the field \(\mathbb{F}\).

Unit quaternions

Definition 2.1.15.

The set \(U(\mathbb{H})\) of quaternions of norm \(1\) (defined in Subsection 1.2.4), together with the binary operation of quaternion multiplication, is called the group of unit quaternions.

Exercises

Exercise 1

Matrices for the dihedral group D4. Let \(H\) denote the \(x\)-axis in the \(x,y\)-plane. The map \(F_H\colon \mathbb{R}^2\to \mathbb{R}^2\) is a linear map whose matrix is \(\displaystyle \left[\begin{array}{cc}1 & 0\\ 0 &
-1\end{array}\right]\text{.}\) The map \(R_{1/4}\colon \mathbb{R}^2\to \mathbb{R}^2\) is a linear map whose matrix is \(\displaystyle \left[\begin{array}{cc}0 & -1\\ 1 &
0\end{array}\right]\text{.}\) Find the matrices for the remaining elements of the dihedral group \(D_4\) as specified in Checkpoint 2.1.6.

Exercise 2

Complex number operations for the dihedral group \(D_4\). Let \(H\) denote the real line \(\mathbb{R}\) in the complex plane \(\mathbb{C}\text{.}\) The map \(F_H\colon \mathbb{C}\to \mathbb{C}\) is complex conjugation \(z\to {z}^\ast\text{.}\) The map \(R_{1/4}\colon \mathbb{C}\to \mathbb{C}\) is the map \(z\to e^{i\pi/2}z=iz\text{.}\) Find the maps \(\mathbb{C}\to \mathbb{C}\) for the remaining elements of the dihedral group \(D_4\) as specified in Checkpoint 2.1.6.

Exercise 3

Recall that a binary operation \((x,y)
\to x\ast y\) is commutative if \(x\ast
y=y\ast x\) for all possible values of \(x,y\text{.}\)

1. Which of the group operations in the examples in this section are commutative? Which are not?
2. Show that \(S_n\) is not commutative for \(n\gt 2\text{.}\)

Exercise 4

One of the properties of a group is the existence of an identity element. This is a group element e with the property that \(eg=ge=g\) for every \( g\) in \(G\text{.}\) Find an identity element for each of the groups in the examples in this section.

Exercise 5

One of the properties of a group is the existence of an inverse element for every element in the group. This means that for every \(g\) in a group \(G\text{,}\) there is an element \(h\) with the property that \(gh=hg=e\text{,}\) where \(e\) is the identity element of the group. Find inverses for the following list of group elements.

1. \([4,2,1,3]\) in \(S_4\)
2. \(R_{120}\) in \(D_6\) (where \(120\) is in degrees)
3. \(\frac{1}{\sqrt{2}}(-1+i)\) in \(S^1\)
4. \(7\) in \(\mathbb{Z}\)
5. \(7\) in \(\mathbb{Z}_9\)
6. \(\displaystyle \left[\begin{array}{cc}1 & 2\\ 2 & 1\end{array}\right]\) in \(GL(2,\mathbb{R})\)
7. \(r=a+bi+cj+dk\) in \(U(\mathbb{H})\)