3.6: Additional exercises

Exercises

Exercise 1

Euclidean subgroup of the Möbius group. 

Let \(\mathbf{E}\) denote the subgroup of the Möbius group \(\mathbf{M}\) generated by rotations and translations, that is, transformations of the type \(z\to e^{it}z\) for \(t\in \mathbb{R}\) and \(z\to z+b\) for \(b\in C\text{.}\) The geometry \((\mathbb{C},\mathbf{E})\) is sometimes called "Euclidean geometry". Is \((\mathbb{C},\mathbf{E})\) equivalent to the Euclidean geometry defined in Subsection 3.1.1? Why or why not?

Exercise 2

Elliptic geometry and spherical geometry.

Is elliptic geometry \((\hat{\mathbb{C}},\mathbf{S})\) equivalent to spherical geometry defined in Subsection 3.1.1? Why or why not?

Exercise 3

Parallel displacements in hyperbolic geometry. 

Let \(T\) be an element of the hyperbolic group \(\mathbf{H}\), with a single fixed point \(p\) and normal form

\begin{equation*}
\frac{1}{Tz-p} = \frac{1}{1-p}+\beta.
\end{equation*}

Show that \(p\beta\) must be a pure imaginary number, that is, there must be a real number \(k\) such that \(p\beta=ki\text{.}\)

Exercise 4

Prove that all elements of the elliptic group \(\mathbf{S}\) are elliptic in the normal form sense, i.e., we have \(|\alpha|=1\) in the normal form expression

\begin{equation*}
\frac{Tz-p}{Tz-q}= \alpha
\frac{z-p}{z-q}.
\end{equation*}

Suggestion: First find the fixed points \(p,q\text{,}\) then put \(z=\infty\) in the normal form equation and solve for \(\alpha\text{.}\)

Exercise 5

Alternative derivation of the formula for elliptic group elements. 

To obtain an explicit formula for elements of the elliptic group, we begin with a necessary condition. Let \(R=s^{-1}\circ
T\circ s\) be the rotation of \(S^2\) that lifts \(T\) via stereographic projection. If \(P,Q\) are a pair of endpoints of a diameter of \(S^2\text{,}\) then \(R(P),R(Q)\) must also be a pair of endpoints of a diameter. Exercise 1.3.3.7 establishes the condition that two complex numbers \(p,q\) are stereographic projections of endpoints of a diameter if and only if \(pq^\ast = -1\text{.}\) Thus we have the following necessary condition for \(T\text{.}\)

\begin{equation}
pq^\ast = -1 \;\;\text{ implies }\;\; Tp(Tq)^\ast =
-1\label{diamendpreservecond}\tag{3.6.1}
\end{equation}

Now suppose that \(Tz=\frac{az+b}{cz+d}\) with \(ad-bc=1\text{.}\) Solving the equation \(Tp =
\frac{-1}{(T(\frac{-1}{p^\ast}))^\ast}\) leads to \(c=-b^\ast\) and \(d=a^\ast\text{.}\) Thus we conclude that \(T\) has the following form.

\begin{equation}
Tz=\frac{az+b}{-b^\ast z+a^\ast},\;\;|a|^2+|b|^2=1\label{elliptictranssu2form}\tag{3.6.2}
\end{equation}

Carry out the computation to derive (3.6.2). Explain why there is no loss of generality by assuming \(ad-bc=1\text{.}\)

Exercise 6

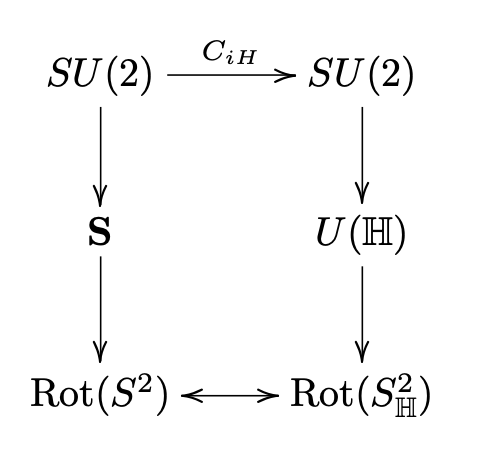
Identifications of U(H) and S with Rot⁡(S2). 

The discussion of elliptic geometry (Section 3.4) establishes two ways to construct rotations from matrices. The purpose of this exercise is to reconcile these identifications. Given \(a,b\in \mathbb{C}\) with \(|a|^2+|b|^2=1\text{,}\) let us define the following objects, all parameterized by \(a,b\text{.}\)

\begin{align*}
M_{a,b} & =\left[\begin{array}{cc}{a}&
{b}\\{-b^\ast}& {a^\ast}\end{array}\right]\\
r_{a,b}& = Re(a)+Im(a)i+Re(b)j+Im(b)k \\
R_{r_{a,b}}& = \left[u\to
r_{a,b}ur_{a,b}^\ast\right]\;\; \text{for }u\in S^2_\mathbb{H}\\
T_{a,b} & = \left[z\to \frac{az+b}{-b^\ast
z+a^\ast}\right] \;\;\text{for }z\in \hat{\mathbb{C}}\\
R_{T_{a,b}} & = s^{-1}\circ T_{a,b}\circ s
\end{align*}

The above objects are organized along two sequences of mappings. The rotation \(R_{r_{a,b}}\) is at the end of the "quaternion path"

\begin{align}
SU(2)& \to U(\mathbb{H})  \to Rot(S^2_\mathbb{H})\label{quatpath}\tag{3.6.3}\\
M_{a,b} &
\to r_{a,b} \to R_{r_{a,b}}\notag
\end{align}

and the rotation \(R_{T_{a,b}}\) is at the end of the "Möbius path"

\begin{align}
SU(2)& \to \S  \to Rot(S^2)\label{mobiuspath}\tag{3.6.4}\\
M_{a,b} &
\to T_{a,b} \to R_{T_{a,b}}.\notag
\end{align}

This problem is about comparing the rotations \(R_{r_{a,b}}\) and \(R_{T_{a,b}}\) (see Table 3.6.1) and reconciling the difference. The angles of rotation are the same, but the axes are different, but only by a reordering of coordinates and a minus sign.

Table 3.6.1. Axis and angle of rotation for quaternion and Möbius rotation constructions

\(R_{v,\theta}\)	axis of rotation \(v\)	angle of rotation \(\theta\)
\(R_{r_{a,b}}\)	\(\frac{(Im(a),Re(b),Im(b))}{\sqrt{1-(Re(a))^2}}\)	\(2\arccos(Re(a))\)
\(R_{T_{a,b}}\)	\(\frac{(Im(b),-Re(b),Im(a))}{\sqrt{1-(Re(a))^2}}\)	\(2\arccos(Re(a))\)

The exercises outlined below verify the values for \(v,\theta\) in Table 3.6.1.

1. Use Proposition 1.2.9 to justify the values for \(v\) and \(\theta\) for \(R_{r_{a,b}}\) in Table 3.6.1.
2. Solve \(T_{a,b}z=z\) to show that one of the fixed points of \(T_{a,b}\) is

   \begin{equation*}
   p=-ib\left( \frac{\sqrt{1-(Re(a))^2} + Im(a)}{|b|^2}\right).
   \end{equation*}

3. Show that \(s\left(\frac{(Im(b),-Re(b),Im(a))}{\sqrt{1-(Re(a))^2}}\right)=p\text{.}\)
4. Show that

   \begin{equation}
   T_{a,b} = s\circ h\circ R_{r_{a,b}}\circ h \circ s^{-1} \label{trhcommute}\tag{3.6.5}
   \end{equation}

   where \(h\colon \mathbb{R}^3\to \mathbb{R}^3\) is given by \((x,y,z)\to (z,-y,z)\text{.}\) Here's one way to do this: evaluate both sides of (3.6.5) on the three points \(p,0,\infty\text{.}\) Explain why this is sufficient! Use quaternion multiplication to evaluate \(R_{r_{a,b}}\text{.}\) For example, \(R_{r_{a,b}}(1,0,0)=r_{a,b}ir_{a,b}^\ast\) under the natural identification \(\mathbb{R}^3\leftrightarrow \mathbb{R}^3_\mathbb{H}\text{.}\)
5. Here is one way to reconcile the quaternion path (3.6.3) with the Möbius path (3.6.4). Let \(H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}
   1& 1 \\ 1& -1\end{array}\right]\) (the matrix \(H\) is sometimes called the Hadamard matrix) and let \(C_{iH}\) denote the map \(M\to (iH)M(iH)^{-1}\text{.}\) Show that the diagram in Figure 3.6.2 commutes. Hint: Notice that \(iH\in SU(2)\) and that \(Q(iH)=\frac{1}{\sqrt{2}}(i+k)\text{,}\) and that \(R_{Q(iH)}=h\text{.}\)

Figure 3.6.2. The map \(C_{iH}\) is given by \(C_{iH}(T)=(iH)T(iH)^{-1}\text{.}\) The column of maps on the left is the "Möbius path", and the column of maps on the right is the "quaternion path".

Figure 3.6.3. Right triangle \(\triangle ABC\)

Exercise 7

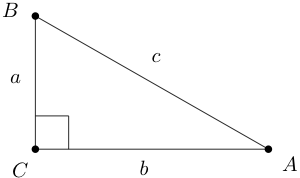
Pythagorean Theorems. 

Let \(\triangle ABC\) be a right triangle with right angle \(\angle C\) with side lengths \(a=d(B,C)\text{,}\) \(b=d(A,C)\text{,}\) and \(c=d(A,B)\) so that the length of the hypotenuse is \(c\text{.}\) See Figure 3.6.3.

1. Prove the following identities.

   \begin{align}
   \cosh \left(\ln\left(\frac{1+u}{1-u}\right)\right) & =
   \frac{1+u^2}{1-u^2}\;\;(0\lt u\lt 1)\label{coshhyperbolicdistidentity}\tag{3.6.6}\\
   \cos(2\arctan u) & = \frac{1-u^2}{1+u^2}\label{cosellipticistidentity}\tag{3.6.7}
   \end{align}

2. The Hyperbolic Pythagorean Theorem. Show that

   \begin{equation}
   \cosh(c)=\cosh(a)\cosh(b)\label{hyperbolicpythagthm}\tag{3.6.8}
   \end{equation}

   if \(T\) is a hyperbolic triangle.
3. The Elliptic Pythagorean Theorem. Show that

   \begin{equation}
   \cos(c)=\cos(a)\cos(b)\label{ellipticpythagthm}\tag{3.6.9}
   \end{equation}

   if \(T\) is an elliptic triangle.

Suggestion: Use a transformation to place \(C\) at \(0\) in \(\mathbb{D}\) or \(\hat{\mathbb{C}}\), with \(A\) is real and \(B\) pure imaginary. Use the formula \(d(p,q) =
\ln((1+u)/(1-u))\) with \(u=\left|\frac{q-p}{1-p^\ast q}\right|\) for hyperbolic distance. Use the formula \(d(p,q) =
2\arctan(u)\text{,}\) with \(u=\left|\frac{q-p}{1+p^\ast
q}\right|\) for elliptic distance. The identities from part \((a)\) will be useful.