Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

3.4: The Point-Slope Form of a Line

  1. Last updated
  2. Save as PDF
  • Page ID
    19695

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    In the last section, we developed the slope-intercept form of a line (y = mx + b). The slope-intercept form of a line is applicable when you’re given the slope and y-intercept of the line. However, there will be times when the y-intercept is unknown.

    Suppose for example, that you are asked to find the equation of a line that passes through a particular point \(P\left(x_{0}, y_{0}\right)\) with slope = m. This situation is pictured in Figure \(\PageIndex{1}\).

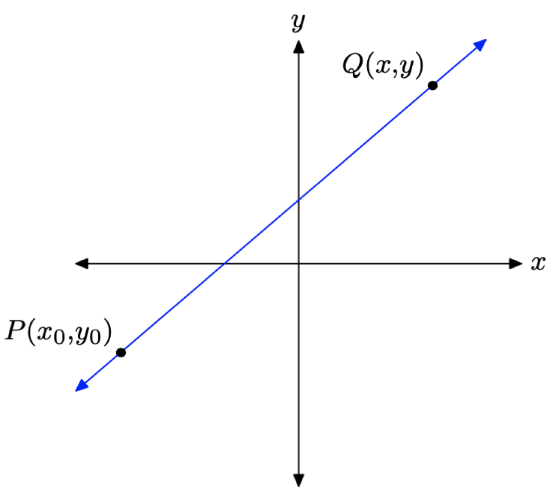
    WeChat7ae165dfc8321137635b442d6de2add0.png
    Figure \(\PageIndex{1}\). A line through \(\left(x_{0}, y_{0}\right)\) with slope m.

    Let the point Q(x, y) be an arbitrary point on the line. We can determine the equation of the line by using the slope formula with points P and Q. Hence,

    \[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y-y_{0}}{x-x_{0}}\]

    Because the slope equals m, we can set Slope = m in this last result to obtain

    \[m=\frac{y-y_{0}}{x-x_{0}}\]

    If we multiply both sides of this last equation by \(x-x_{0}\), we get

    \[m\left(x-x_{0}\right)=y-y_{0}\]

    or exchanging sides of this last equation,

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    This last result is the equation of the line.

    The Point-Slope Form of a Line

    If line L passes through the point \(\left(x_{0}, y_{0}\right)\) and has slope m, then the equation of the line is \[y-y_{0}=m\left(x-x_{0}\right)\] This form of the equation of a line is called the point-slope form.

    To use the point-slope form of a line, follow these steps.

    Procedure for Using the Point-Slope Form of a Line

    When given the slope of a line and a point on the line, use the point-slope form as follows:

    1. Substitute the given slope for m in the formula \(y-y_{0}=m\left(x-x_{0}\right)\).
    2. Substitute the coordinates of the given point for x0 and y0 in the formula \(y-y_{0}=m\left(x-x_{0}\right)\).

    For example, if the line has slope −2 and passes through the point (3, 4), then substitute \(m=-2, x_{0}=3,\) and \(y_{0}=4\) in the formula \(y-y_{0}=m\left(x-x_{0}\right)\) to obtain \[y-4=-2(x-3)\].

    Example \(\PageIndex{1}\)

    Draw the line that passes through the point P(−3, −2) and has slope m = 1/2. Use the point-slope form to determine the equation of the line.

    Solution

    First, plot the point P(−3, −2), as shown in Figure \(\PageIndex{2}\)(a). Starting from the point P(−3, −2), move 2 units to the right and 1 unit up to the point Q(−1, −1). The line through the points P and Q in Figure \(\PageIndex{2}\)(a) now has slope m = 1/2.

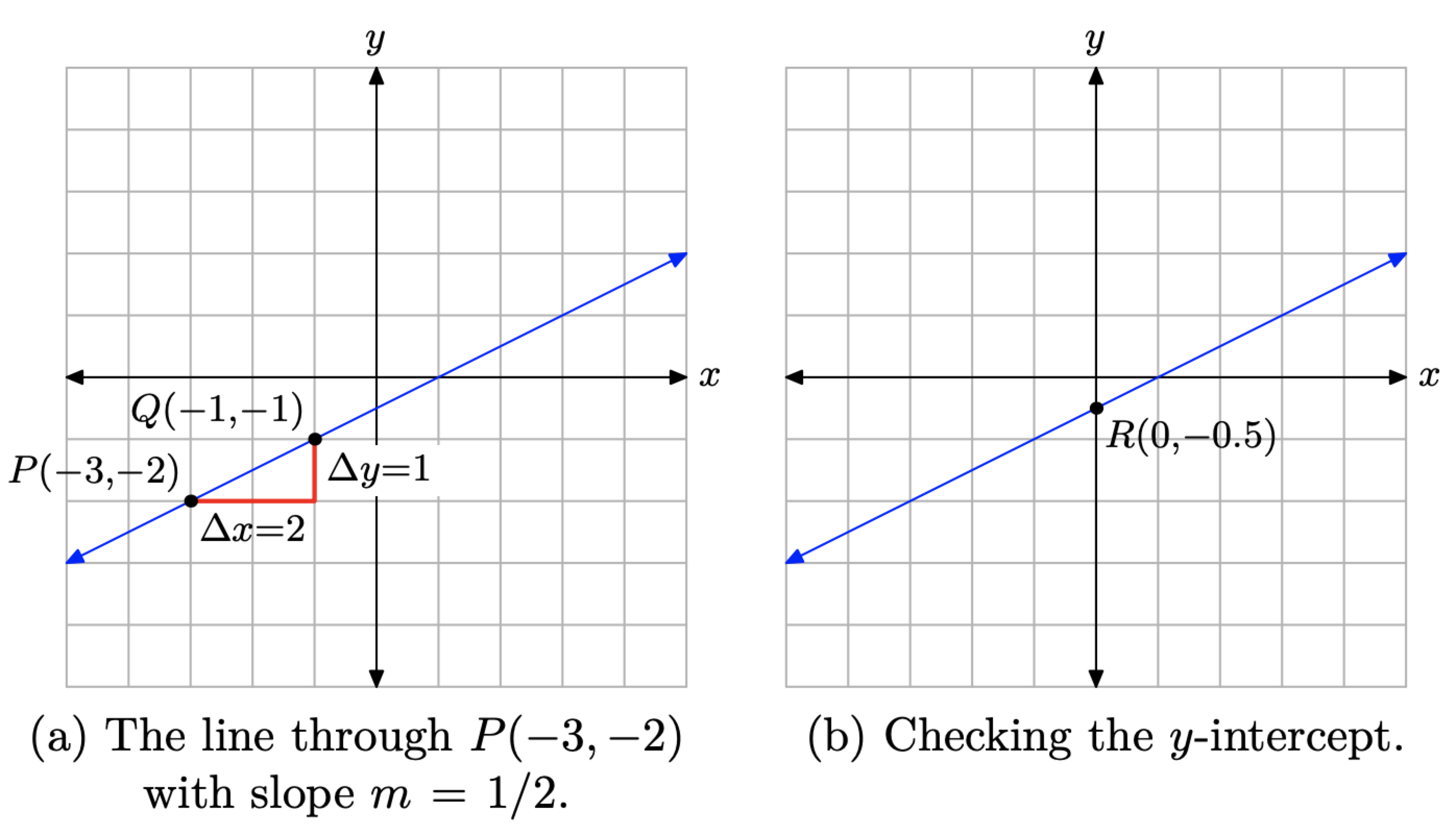
    WeChatb11c39993f9ab17a0098dc9991df0cb7.png
    Figure \(\PageIndex{2}\)

    To determine the equation of the line in Figure \(\PageIndex{2}\)(a), we will use the point-slope form of the line

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    The slope of the line is m = 1/2 and the given point is P(−3, −2), so\(\left(x_{0}, y_{0}\right)=(−3, −2)\). In equation (3), set \(m=1 / 2, x_{0}=-3,\) and \(y_{0}=-2\), obtaining

    \[y-(-2)=\frac{1}{2}(x-(-3))\]

    or equivalently,

    \[y+2=\frac{1}{2}(x+3)\]

    This is the equation of the line in Figure \(\PageIndex{2}\)(a).

    As a check, we’ve estimated the y-intercept of the line in Figure \(\PageIndex{2}\)(b) as R(0, −0.5). Let’s place equation (4) in slope-intercept form to determine the exact value of the y-intercept. First, distribute 1/2 to get

    \[y+2=\frac{1}{2} x+\frac{3}{2}\]

    Subtract 2 from both sides of this last equation.

    \[y=\frac{1}{2} x+\frac{3}{2}-2\]

    Make equivalent fractions with a common denominator and simplify.

    \[\begin{array}{l}{y=\frac{1}{2} x+\frac{3}{2}-\frac{4}{2}} \\ {y=\frac{1}{2} x-\frac{1}{2}}\end{array}\]

    Comparing equation (5) with y = mx+b gives us b = −1/2. This is the exact y-value of the y-intercept. Note that this result compares exactly with the y-value of point R in Figure \(\PageIndex{2}\)(b). This is a bit lucky. Don’t expect to get an exact comparison every time. However, if the comparison is not close, look for an error in your work, either in your computations or in your graph.

    Let’s look at another example.

    Example \(\PageIndex{2}\)

    Find the equation of the line passing through the points P(−3, 2) and Q(2, −1). Place your final answer in standard form.

    Solution

    Again, to help keep our focus, we draw the line passing through the points P(−3, 2) and Q(2, −1) in Figure \(\PageIndex{3}\).

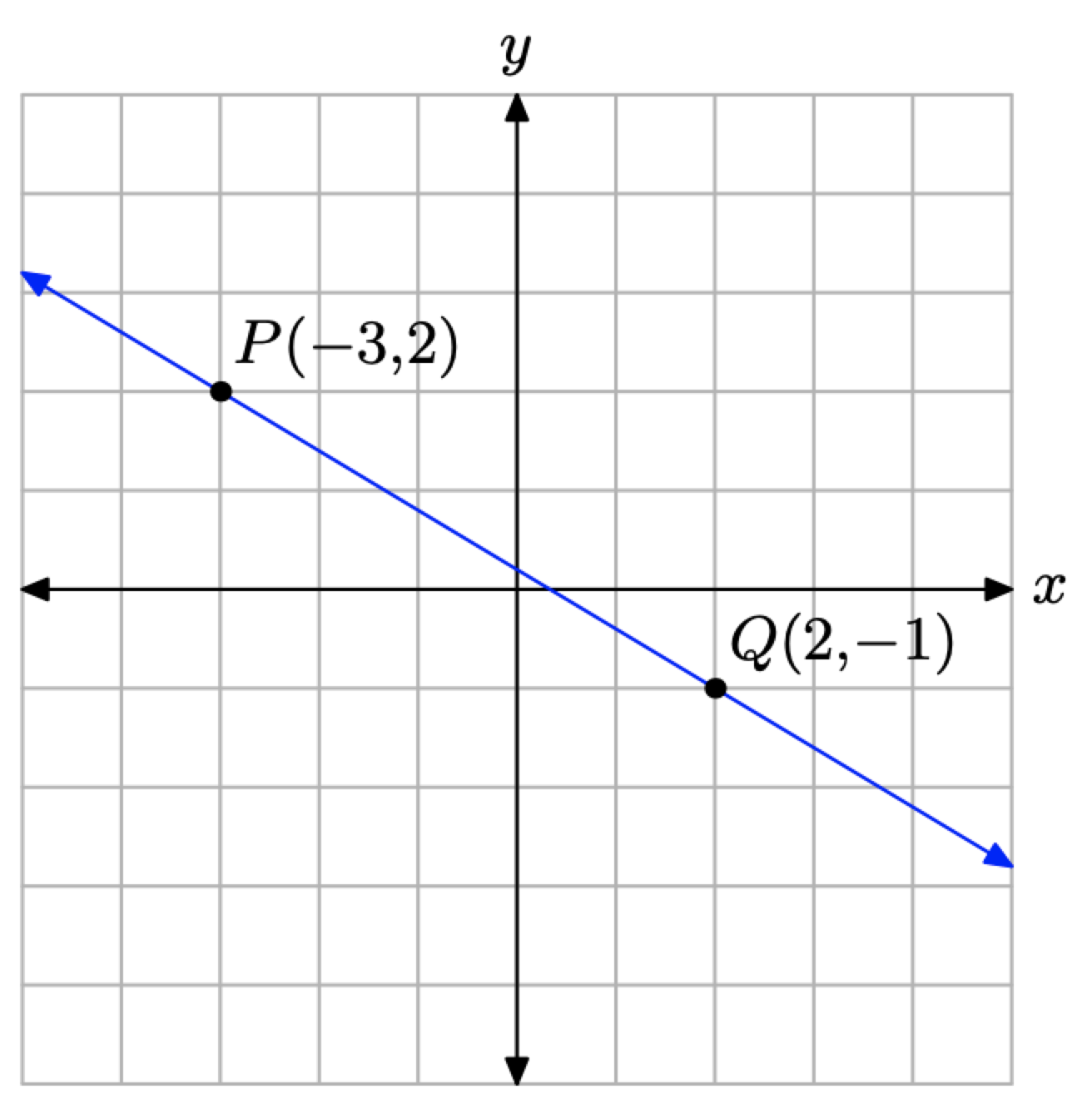
    WeChata0d7e316a7412734afa037efaf06e7b9.png
    Figure \(\PageIndex{3}\). The line through points P(−3, 2) and Q(2, −1).

    Use the slope formula to determine the slope of the line through the points P(−3, 2) and Q(2, −1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{-1-2}{2-(-3)}=-\frac{3}{5}\]

    We’ll use the point-slope form of the line

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    Let’s use point P(−3, 2) as the given point \(\left(x_{0}, y_{0}\right)\). That is, \(\left(x_{0}, y_{0}\right)=(-3,2)\). Substitute \(m=-3 / 5, x_{0}=-3,\) and \(y_{0}=2\) in equation (7), obtaining

    \[y-2=-\frac{3}{5}(x-(-3))\]

    This is the equation of the line passing through the points P and Q.

    Alternatively, we could also use the point Q(2, −1) as the given point \(\left(x_{0}, y_{0}\right)\). That is, \(\left(x_{0}, y_{0}\right)=(2,-1)\). Substitute \(m=-3 / 5, x_{0}=2,\) and \(y_{0}=-1\) in the point-slope form (7), obtaining

    \[y-(-1)=-\frac{3}{5}(x-2)\]

    This too, is the equation of the line passing through the points P and Q.

    How can the equations (8) and (9) both be the equation of the line through P and Q, yet look so distinctly different? Let’s place each equation in standard form \(Ax + By = C\) and compare the results.

    If we start with equation (8) and distribute the slope,

    \[\begin{array}{l}{y-2=-\frac{3}{5}(x-(-3))} \\ {y-2=-\frac{3}{5} x-\frac{9}{5}}\end{array}\]

    Multiply both sides by the common denominator 5 to clear the fractions.

    \[\begin{aligned} 5(y-2) &=5\left(-\frac{3}{5} x-\frac{9}{5}\right) \\ 5 y-10 &=-3 x-9 \end{aligned}\]

    Add 3x to both sides of the equation, then add 10 to both sides of the equation to obtain

    \[3 x+5 y=1\]

    Place equation (9) in standard form in a similar manner. First, start with equation (9) and distribute the slope,

    \[\begin{aligned} y-(-1) &=-\frac{3}{5}(x-2) \\ y+1 &=-\frac{3}{5} x+\frac{6}{5} \end{aligned}\]

    Next, multiply both sides of this last result by 5 to clear the fractions from the equation.

    \[\begin{aligned} 5(y+1) &=5\left(-\frac{3}{5} x+\frac{6}{5}\right) \\ 5 y+5 &=-3 x+6 \end{aligned}\]

    Finally, add 3x to both sides of the equation, then subtract 5 from both sides of the equation to obtain

    \[3 x+5 y=1\]

    Note that equation (11) is identical to equation (10). Thus, it doesn’t matter which point you use in the point-slope form. Both lead to the same result.

    Parallel Lines

    Recall that slope controls the “steepness” of a line. Consequently, if two lines are parallel, they must have the same “steepness” or slope. Let’s look at an example of parallel lines.

    Example \(\PageIndex{3}\)

    Find the equation of the line that passes through the point P(−2, 2) that is parallel to the line passing through the points Q(−3, −1) and R(2, 1).

    Solution

    First, to help us stay focused, we draw the line through the points Q(−3, −1) and R(2, 1), then plot the point P(−2, 2), as shown in Figure \(\PageIndex{4}\)(a).

    We can use the slope formula to calculate the slope of the line passing through the points Q(−3, −1) and R(2, 1).

    \[m=\frac{\Delta y}{\Delta x}=\frac{1-(-1)}{2-(-3)}=\frac{2}{5}\]

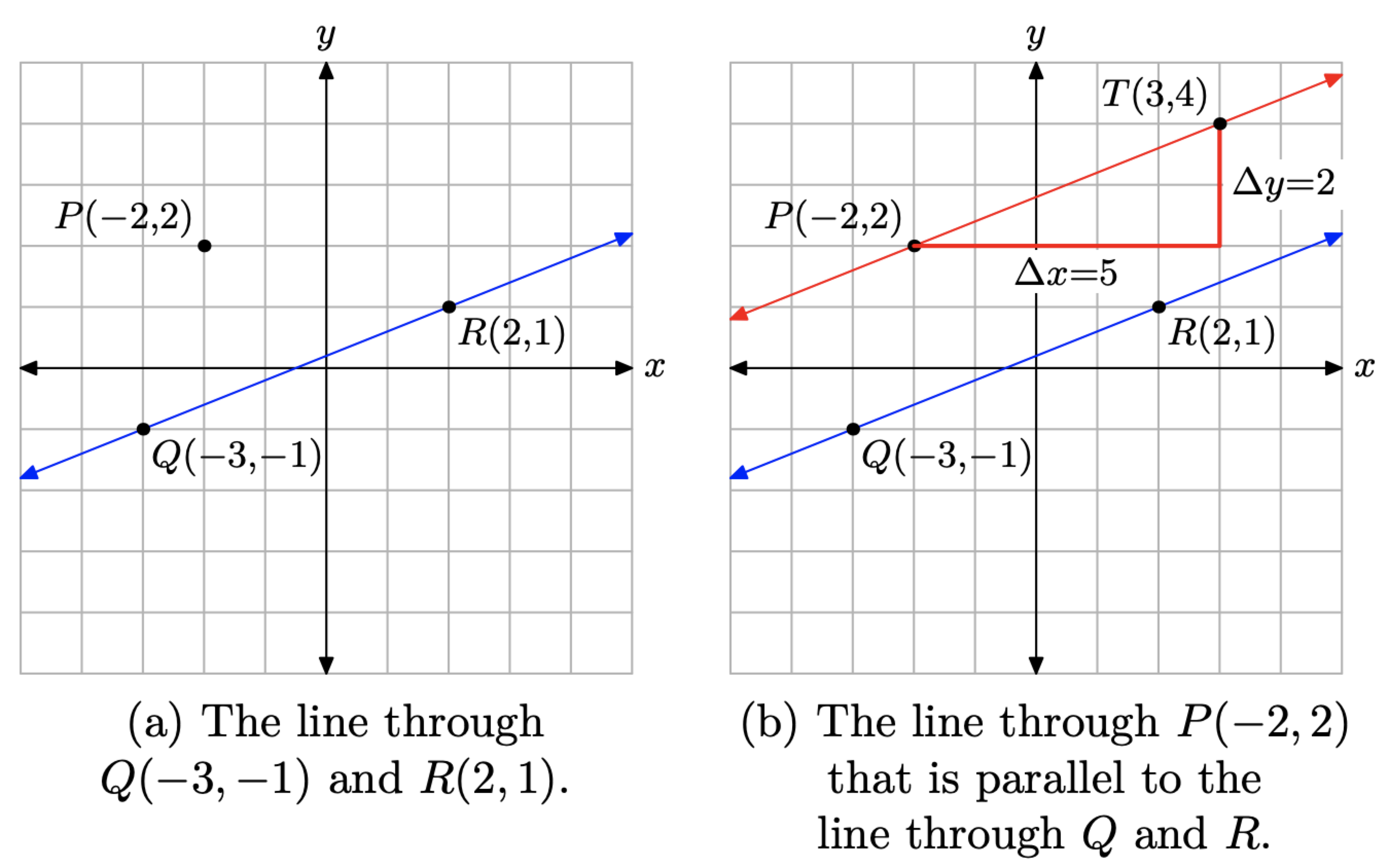
    WeChatf91e04129da47aa1d1b93440e15a29bd.png
    Figure \(\PageIndex{4}\).

    We now draw a line through the point P(−2, 2) that is parallel to the line through the points Q and R. Parallel lines must have the same slope, so we start at the point P(−2, 2), “run” 5 units to the right, then “rise” 2 units up to the point T(3, 4), as shown in Figure \(\PageIndex{4}\)(b).

    We seek the equation of the line through the points P and T. We’ll use the pointslope form of the line

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    We’ll use the point P(−2, 2) as the given point \(\left(x_{0}, y_{0}\right)\). That is, \(\left(x_{0}, y_{0}\right) = (−2, 2)\). The line through P has slope 2/5. Substitute \(m=2 / 5, x_{0}=-2,\) and \(y_{0}=2\) in equation (13) to obtain

    \[y-2=\frac{2}{5}(x-(-2))\]

    Let’s place the equation (14) in standard form. Distribute the slope, then clear fractions by multiplying both sides of the resulting equation by 5.

    \[\begin{aligned} y-2 &=\frac{2}{5} x+\frac{4}{5} \\ 5(y-2) &=5\left(\frac{2}{5} x+\frac{4}{5}\right) \\ 5 y-10 &=2 x+4 \end{aligned}\]

    Finally, subtract 5y from both sides of the last equation, then subtract 4 from both sides of the equation, obtaining

    \[-14=2 x-5 y\]

    or equivalently,

    \[2 x-5 y=-14\]

    This is the standard form of the equation of the line passing through the point P and parallel to the line passing through the points Q and R.

    Perpendicular Lines

    Suppose that two lines \(L_{1}\) and \(L_{2}\) have slopes \(m_{1}\) and \(m_{2}\), respectively. Recall (see the section on Slope) that if \(L_{1}\) and \(L_{2}\) are perpendicular, then the product of their slopes is \(m_{1} m_{2}=-1\). Alternatively, the slope of the first line is the negative reciprocal of the second line, and vice-versa; i.e., \(m_{1}=-1 / m_{2}\) and \(m_{2}=-1 / m_{1}\). Let’s look at an example of perpendicular lines.

    Example \(\PageIndex{4}\)

    Find the equation of the line passing through the point P(−4, −4) that is perpendicular to the line 4x + 3y = 12.

    Solution

    It will help our focus if we draw the given line 4x + 3y = 12. The easiest way to plot a line in standard form Ax + By = C is to find the x- and y-intercepts.

    \[\begin{array}{rlrrll}{4 x+3 y} & {=}&{12} & {4 x+3 y} & {=}&{12} \\ {4 x+3(0)} & {=}&{12} & {4(0)+3 y} & {=}&{12} \\ {4 x} & {=}&{12} & {3 y} & {=}&{12} \\ {x} & {=}&{3} & {y} & {=}&{4}\end{array}\]

    Plot the x- and y-intercepts R(3, 0) and S(0, 4) as shown in Figure \(\PageIndex{5}\)(a). The line through points R and S is the graph of the equation 4x + 3y = 12.

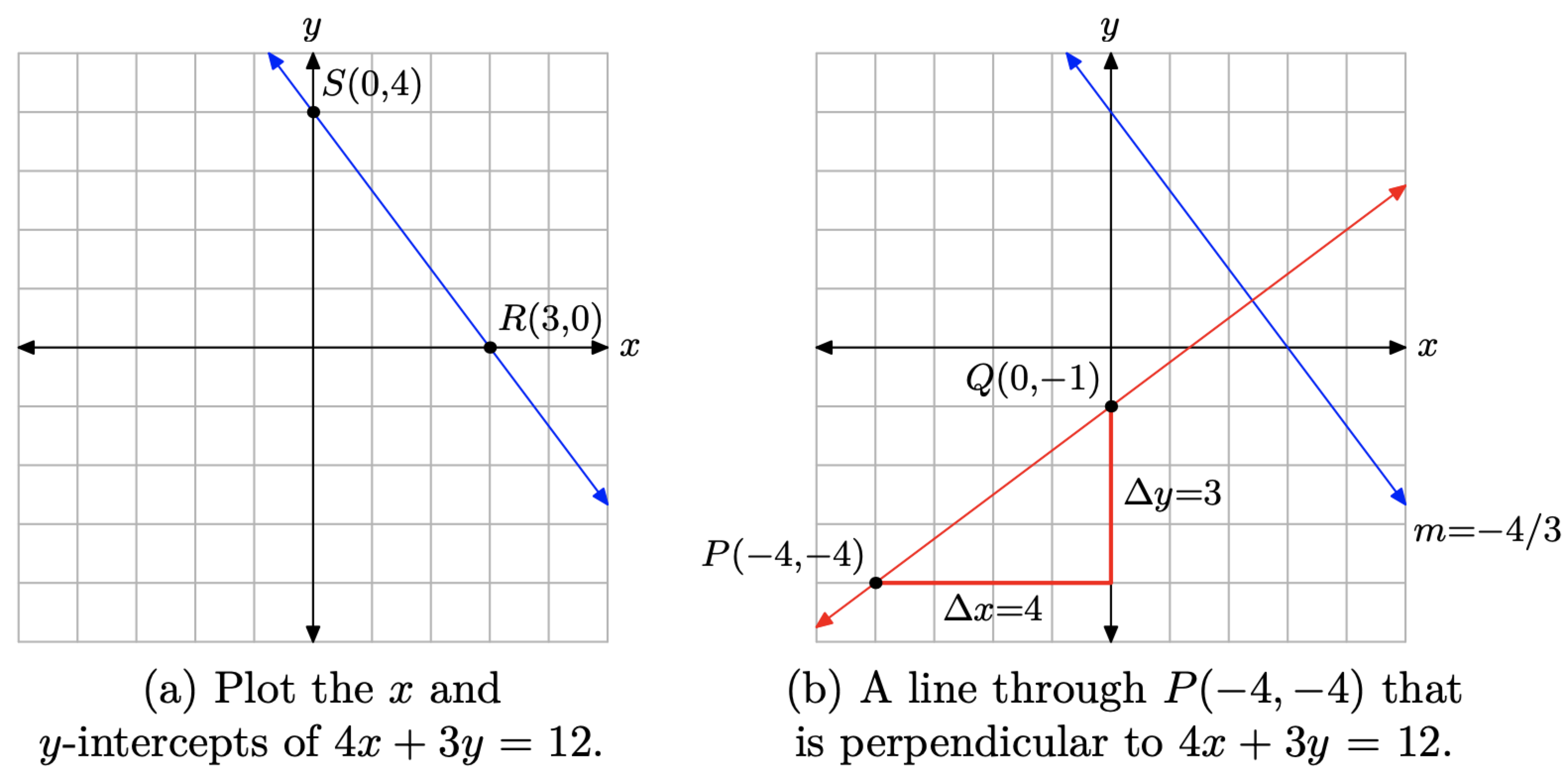
    WeChatf5a79539226b56f42d05801aae5a4375.png
    Figure \(\PageIndex{5}\)

    Next, determine the slope of the line 4x + 3y = 12 by placing this equation in slope-intercept form (i.e., solve the equation 4x + 3y = 12 for y)

    \[\begin{aligned} 4 x+3 y &=12 \\ 3 y &=-4 x+12 \\ y &=-\frac{4}{3} x+4 \end{aligned}\]

    If two lines are perpendicular, then their slopes are negative reciprocals of one another. Therefore, the slope of the line that is perpendicular to the line 4x + 3y = 12 (which has slope −4/3) is m = 3/4. Our second line must pass through the point P(−4, −4). To draw this second line, first plot the point P(−4, −4), then move 4 units to the right and 3 units upward to the point Q(0, −1), as shown in Figure \(\PageIndex{5}\)(b). The line through the points P and Q is perpendicular to the line 4x + 3y = 12.

    To determine the equation of the line through the points P and Q, we will use the point-slope form of the line, namely

    \[y-y_{0}=m\left(x-x_{0}\right)\]

    The slope of the line through points P and Q is m = 3/4. If we use the point P(−4, −4), then \(\left(x_{0}, y_{0}\right)=(-4,-4)\). Set \(m=3 / 4, x_{0}=-4,\) and \(y_{0}=-4\) in equation (16), obtaining

    \[y-(-4)=\frac{3}{4}(x-(-4))\]

    or equivalently,

    \[y+4=\frac{3}{4}(x+4)\]

    Alternatively, we could use the slope-intercept form of the line. We know that the line through points P and Q in Figure \(\PageIndex{5}\)(b) crosses the y-axis at Q(0, −1). So, with slope m = 3/4 and y-coordinate of the y-intercept b = −1, the slope-intercept form y = mx + b becomes

    \[y=\frac{3}{4} x-1\]

    On the other hand, if we solve equation (17) for y,

    \[\begin{aligned} y+4 &=\frac{3}{4}(x+4) \\ y+4 &=\frac{3}{4} x+3 \\ y &=\frac{3}{4} x-1 \end{aligned}\]

    Note that this is identical to the result found using the slope-intercept form above.

    It is comforting to note that the two forms (point-slope and slope-intercept) give the same result, but how do we determine the most efficient form to use for a particular problem? Here’s a good hint.

    Determining the Form of the Line to Use

    Here is some sound advice when you are trying to determine whether to use the slope-intercept form or the pointslope form of a line.

    • If you are given the slope and the y-intercept, use the slope-intercept form y = mx + b.
    • If you are given a point (other than the y-intercept) and the slope, use the point-slope form \(y-y_{0}=m\left(x-x_{0}\right)\).

    Applications of Linear Functions

    In this section we will look at some applications of linear functions. We begin by developing a function relating Fahrenheit and Celsius temperature.

    Example \(\PageIndex{5}\)

    Water freezes at \(32^{\circ} F\) and \(0^{\circ} \mathrm{C}\). Water boils at \(212^{\circ} F\) and \(100^{\circ} \mathrm{C}\). F and C are abbreviations for Fahrenheit and Celsius temperature scales, respectively. Assuming a linear relationship, develop a model relating Fahrenheit and Celsius temperature.

    Solution

    First, to help keep our focus, we set up a coordinate system on a sheet of graph paper. In Figure \(\PageIndex{6}\), we’ve decided to make the Celsius temperature the dependent variable and have assigned the Celsius temperature to the vertical axis. Similarly, we’ve declared the Fahrenheit temperature the independent variable and assigned it to the horizontal axis.

    Interpret the given data:

    • Water freezes at \(32^{\circ} F\) and \(0^{\circ} C\). This gives us the point (F, C) = (32, 0), which we plot in Figure \(\PageIndex{6}\).
    • Water boils at \(212^{\circ} F\) and \(100^{\circ} C\). This gives us the point (F, C) = (212, 100), which we plot in Figure \(\PageIndex{6}\).

    Now we are on familiar ground. We want to find the equation of the line through these two points, which is the same type of problem we tackled in Example 6. First, use the points (32, 0) and (212, 100) to determine the slope of the line.

    \[m=\frac{\Delta C}{\Delta F}=\frac{100-0}{212-32}=\frac{100}{180}=\frac{5}{9}\]

    We will now use the point-slope form of the line, \(y-y_{0}=m\left(x-x_{0}\right)\) with m = 5/9 and \(\left(x_{0}, y_{0}\right)=(32,0)\). Substitute \(m=5 / 9, x_{0}=32,\) and \(y_{0}=0\) in \(y-y_{0}=m\left(x-x_{0}\right)\) to obtain

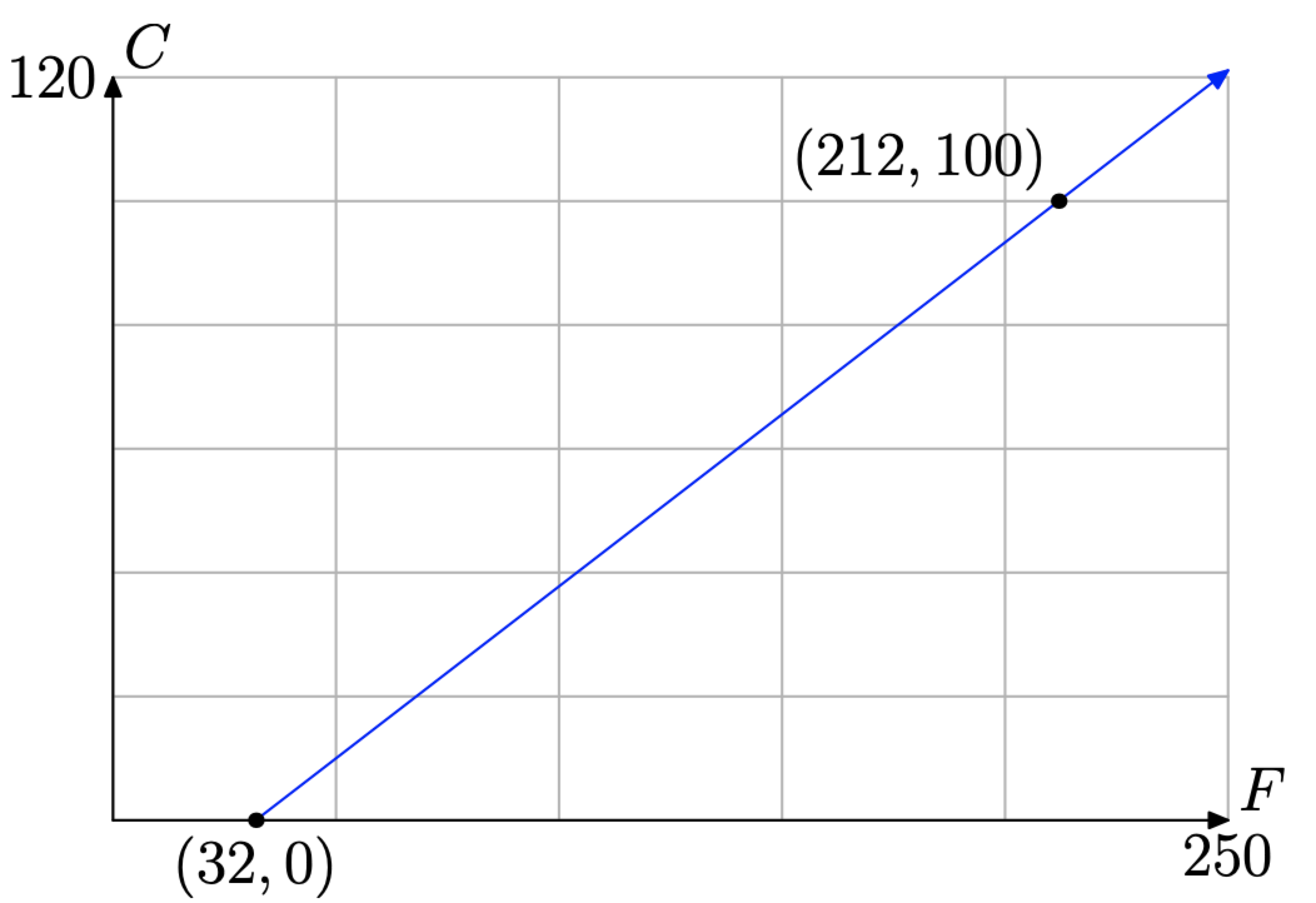
    WeChat592ee9ac052697196b626cb1b26fab84.png
    Figure \(\PageIndex{6}\). Plotting Celsius temperature versus Fahrenheit temperature

    \[y-0=\frac{5}{9}(x-32)\]

    However, our dependent axis is labeled C, not y, and our independent axis is labeled F, not x. So, we must replace y and x in equation (20) with C and F, respectively, obtaining

    \[C=\frac{5}{9}(F-32)\]

    This result in equation (21) expresses the Celsius temperature as a function of the Fahrenheit temperature. Alternatively, we could also use function notation and write

    \[C(F)=\frac{5}{9}(F-32)\]

    Suppose that we know that the Fahrenheit temperature outside is \(80^{\circ} \mathrm{F}\) and we wish to express this using the Celsius scale. To do so, we simply evaluate C(80), as in

    \[C(80)=\frac{5}{9}(80-32) \approx 26.6\]

    Hence, the Celsius temperature is approximately \(26.6^{\circ} \mathrm{C}\).

    On the other hand, suppose that we know the Celsius temperature on a metal roof is \(80^{\circ} \mathrm{C}\) and we wish to find the Fahrenheit temperature. To do so, we need to solve

    \[C(F)=80\]

    for F, or equivalently,

    \[\frac{5}{9}(F-32)=80\]

    Multiply both sides by 9 to obtain

    \[5(F-32)=720\]

    then divide both sides of the result by 5 to obtain

    \[F-32=144\]

    Adding 32 to both sides of this last result produces the Fahrenheit temperature \(F = 176^{\circ} \mathrm{F}\). Wow, that’s hot!