2.7: Synthetic Division

The process for polynomial long division (like the process for numerical long division) has been separated somewhat from its logical underpinnings for a more efficient method to arrive at an answer. For particular types of polynomial long division, we can even take this abstraction one step further. Synthetic Division is a handy shortcut for polynomial long division problems in which we are dividing by a linear polynomial. This means that the highest power of $x$ we are dividing by needs to be $x^{1}$. This limits the usefulness of Synthetic Division, but it will serve us well for certain purposes. Let's examine where the coefficients in our answer come from when we divide by a linear polynomial:

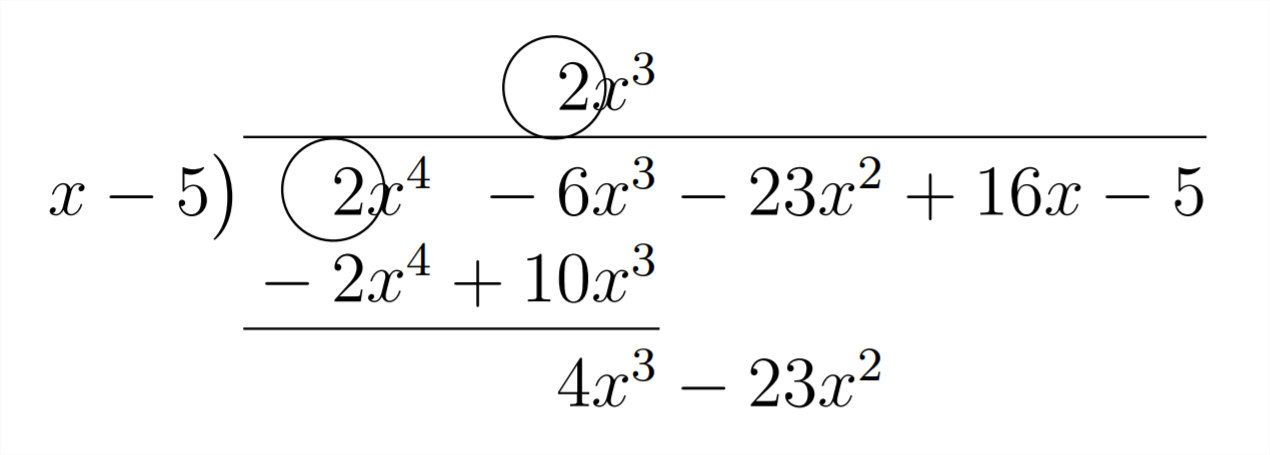
Notice that the first coefficient in the answer is the same as the first coefficient in the polynomial we're dividing into. This is because we're dividing by a polynomial in the form $1 x^{1}-a .$ This also makes the power of the first term in the answer one less than the power of the polynomial we are dividing into. Let's see where the subsequent coefficients in the answer come from:

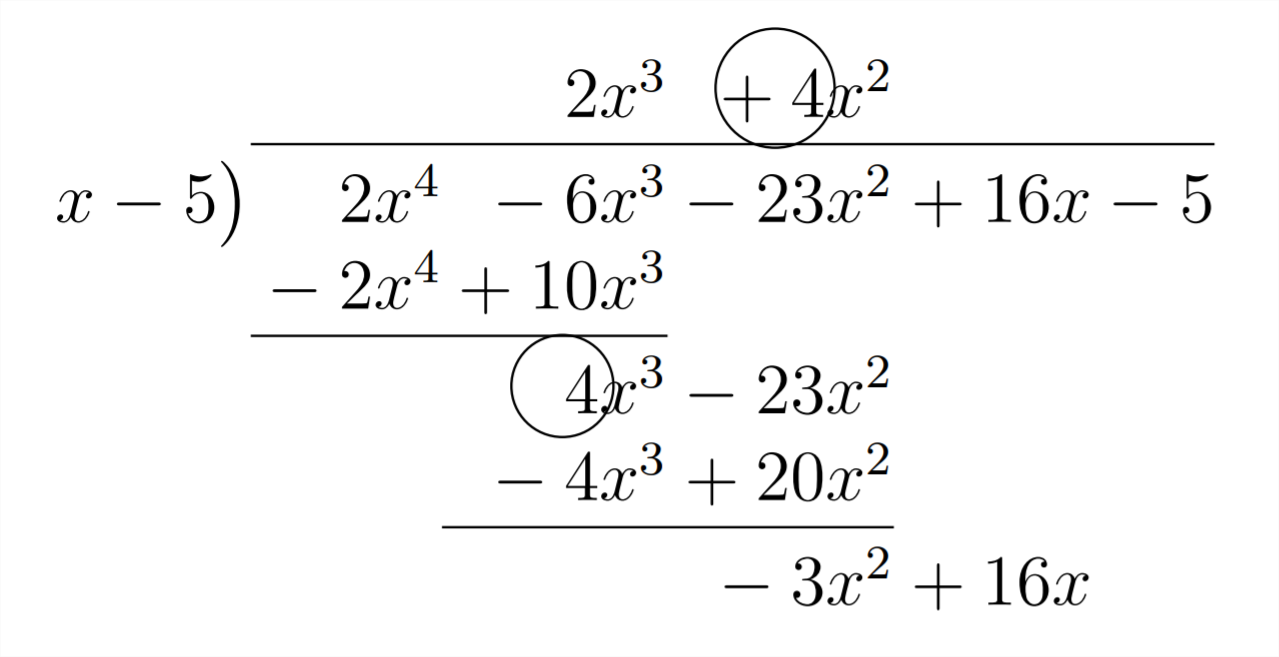
The next coefficient in the answer (4) comes from the combination of the -6 and the $+10 .$ The +10 came from multiplying the 2 in the answer by the 5 in the divisor $x-5 .$ The next coefficient in the answer will be $-3,$ which comes from multiplying the 4 (in the answer) by the 5 (in the divisor) and combining it with the -23 in the polynomial we're dividing into:

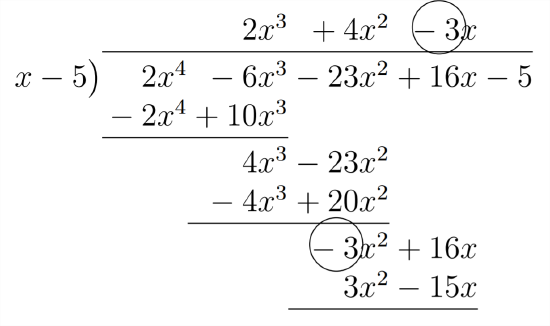
The last part of our answer will come from multiplying the -3 in the answer times the 5 in the divisor (making -15 ) and combining this with the +16 in the polynomial we're dividing into:

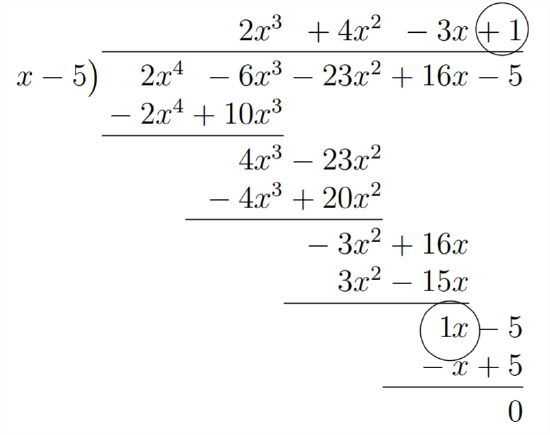
The process of Synthetic Division uses these relationships as a shortcut to finding the answer. The set-up for a Synthetic Division problem is shown below:

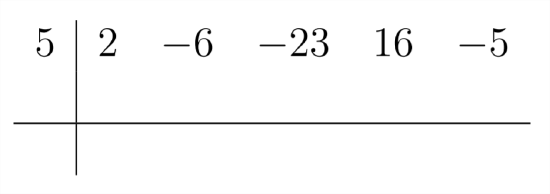
This set-up allows us to complete the division problem $\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}.$

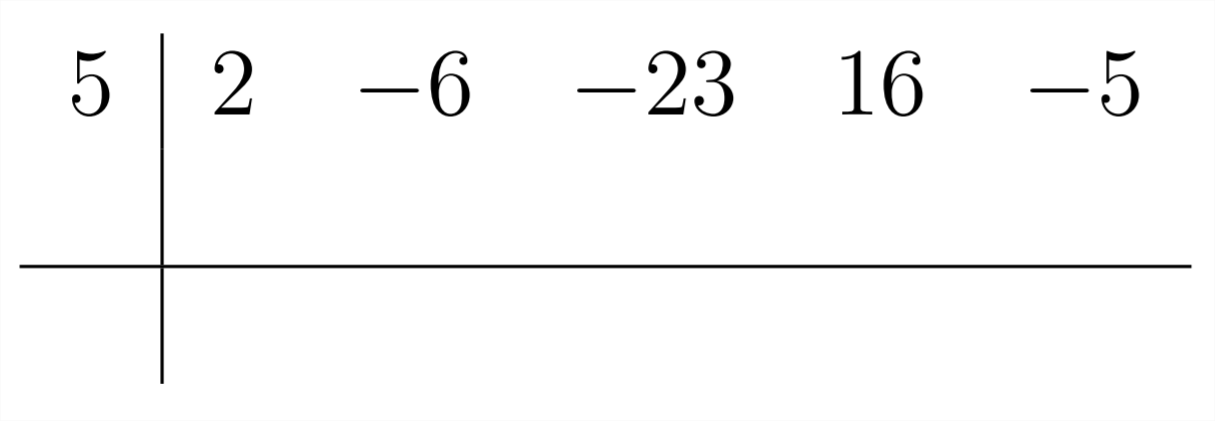
The first coefficient in the answer is the same as the first coefficient in the polynomial we're dividing into:

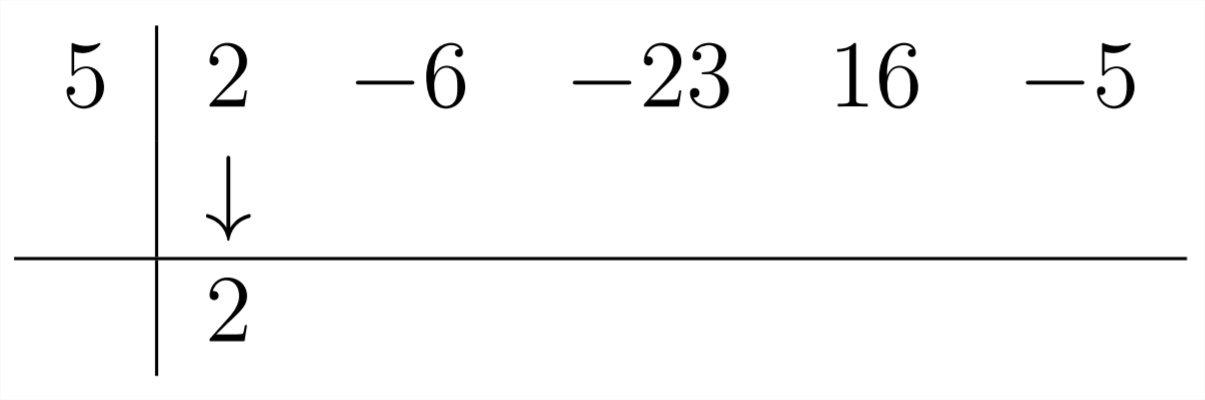
To get the next coefficient, we multiply the 2 by the 5 to get +10 and flll this in under the -6:

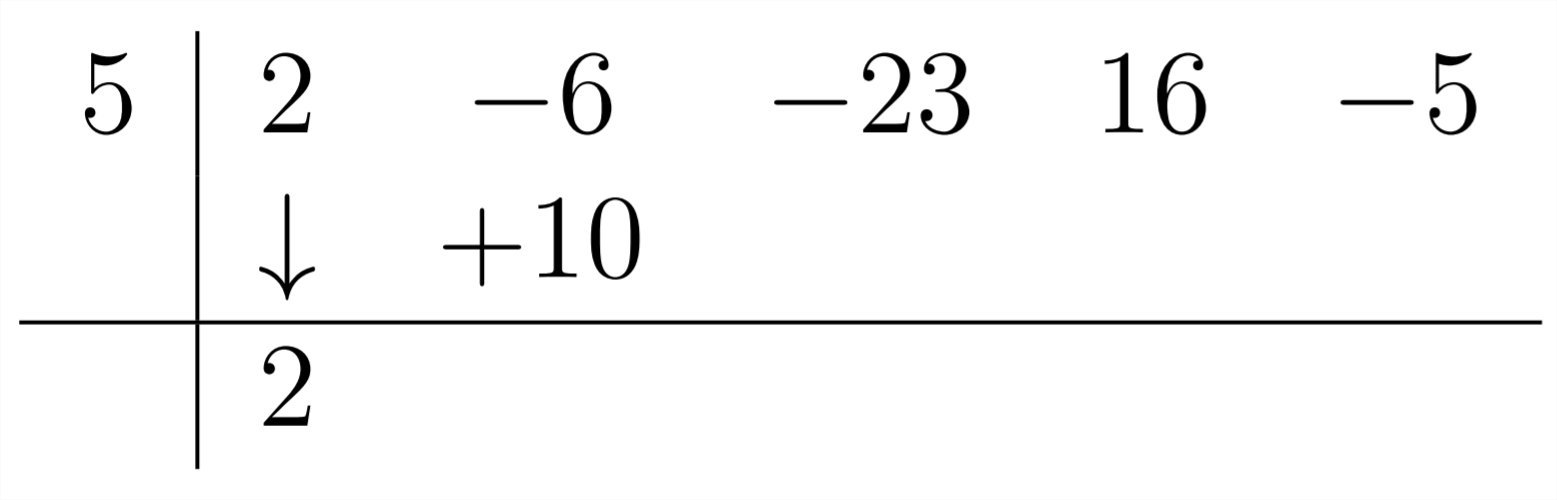
Then, $-6+10=+4,$ which is the next coefficient in the answer:

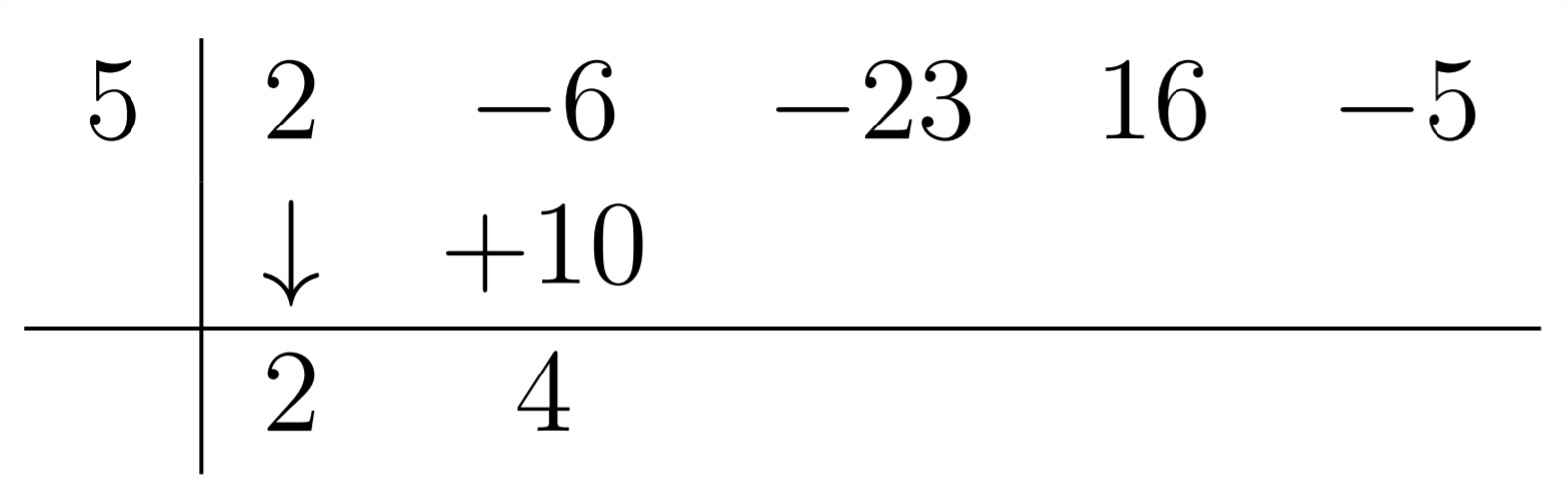
Then, we continue this process, multiplying the 4 by the 5 to get 20 and combining this with the $-23:-23+20=-3:$

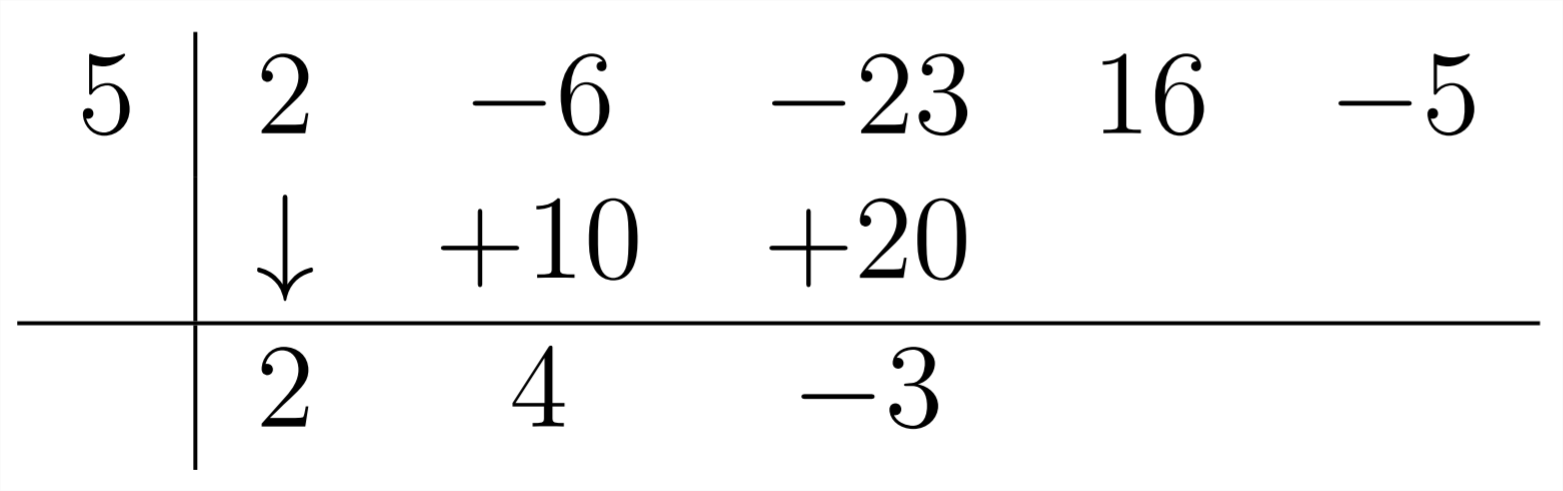
Next, multiply the -3 by the 5 and combine the resulting -15 with the 16:

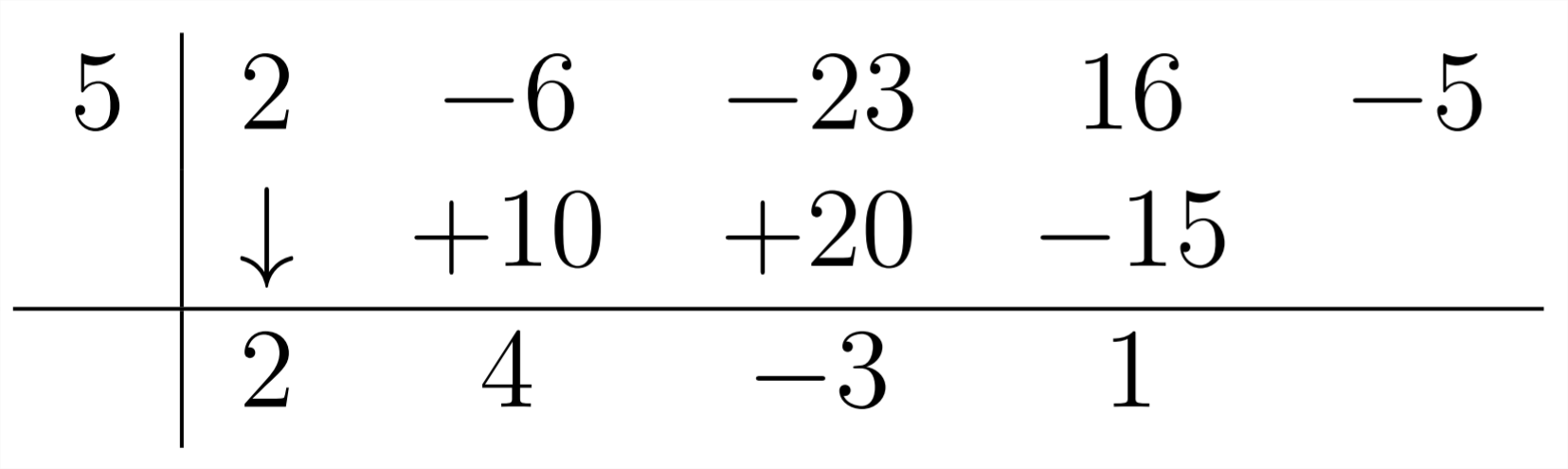
In the last step, multiply the 1 times the 5 and combine the result with the -5 in the problem to get zero:

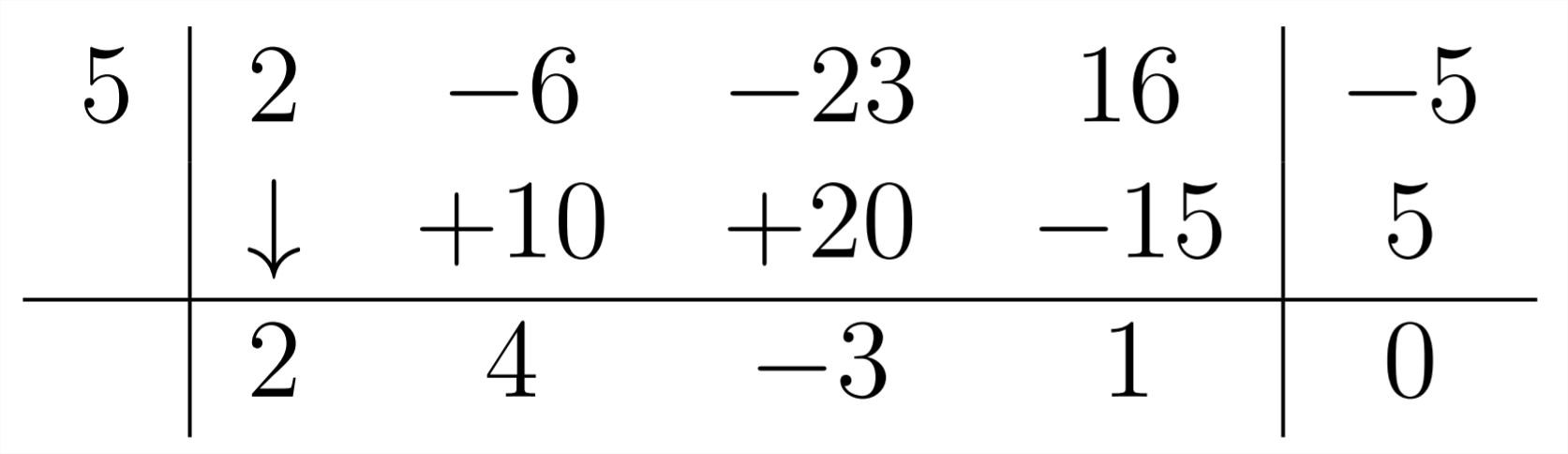
This last coefficient represents the remainder - in this case 0. The other numerals in the answer represent the coefficients for the powers of $x$ in the answer. On the far right is the remainder, then the constant $\left(x^{0}\right)$ term, then the linear $\left(x^{1}\right)$ term and so on:

$\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}=2 x^{3}+4 x^{2}-3 x+1$
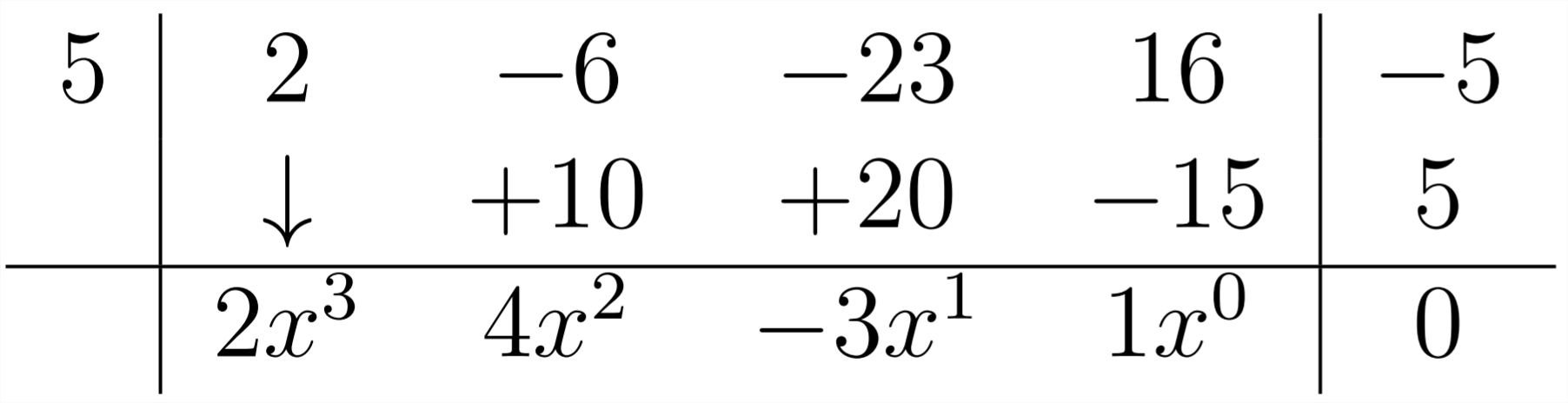
Let's look at another example:

Example
Use Synthetic Division to divide:
$\frac{3 x^{3}+5 x^{2}-9 x+9}{x+3}$
since Synthetic Division is set up to divide by $x-a$, if we're dividing by $x+3$ we'll need to use a -3 in the Synthetic Division:

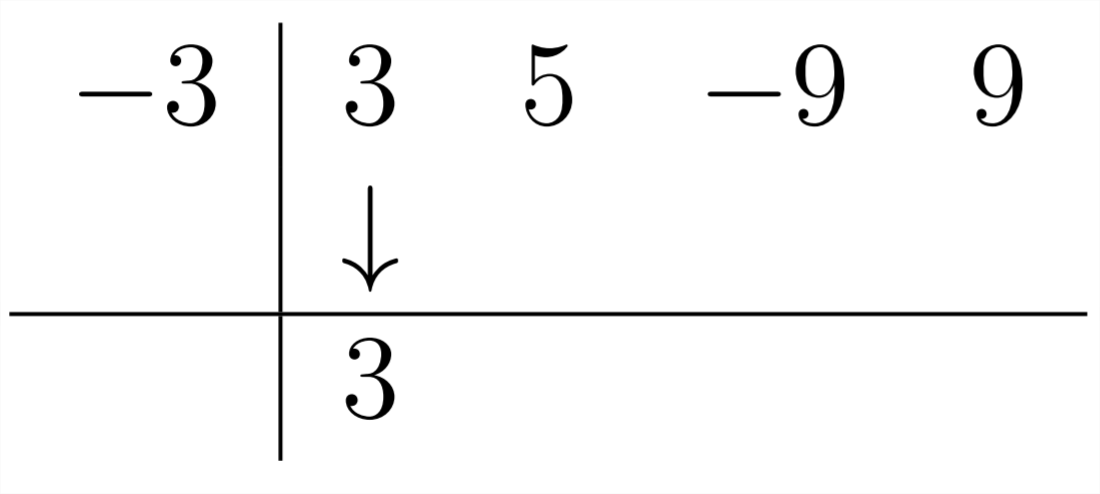
Then, $3 *-3=-9$

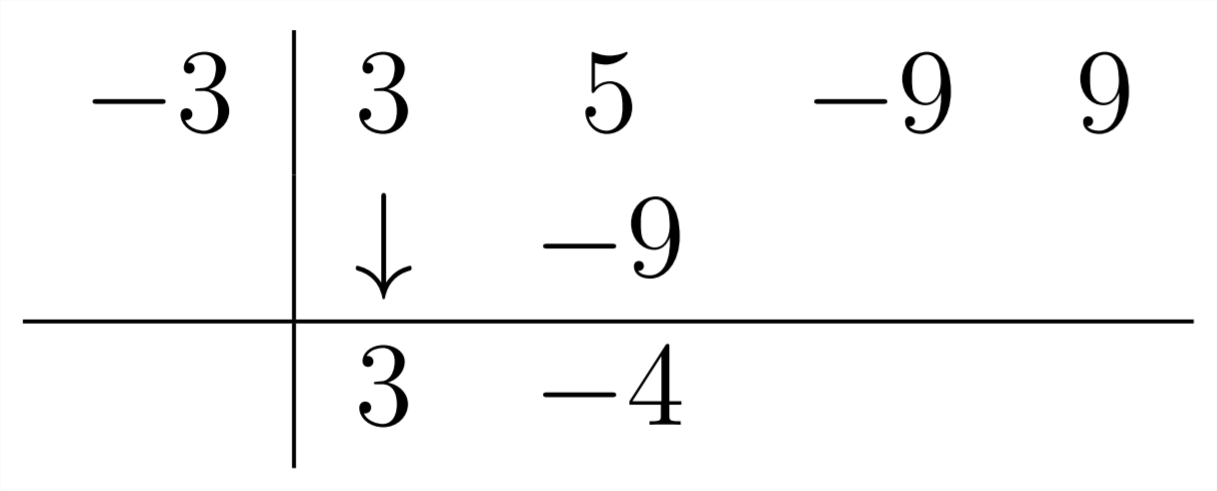
Next, $-4 *-3=+12$

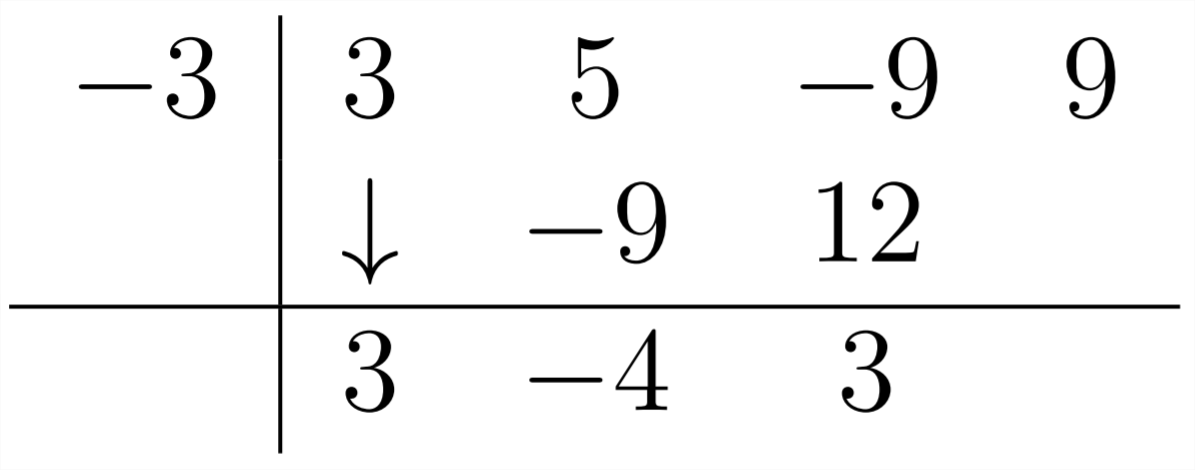
And this example also has a zero remainder:

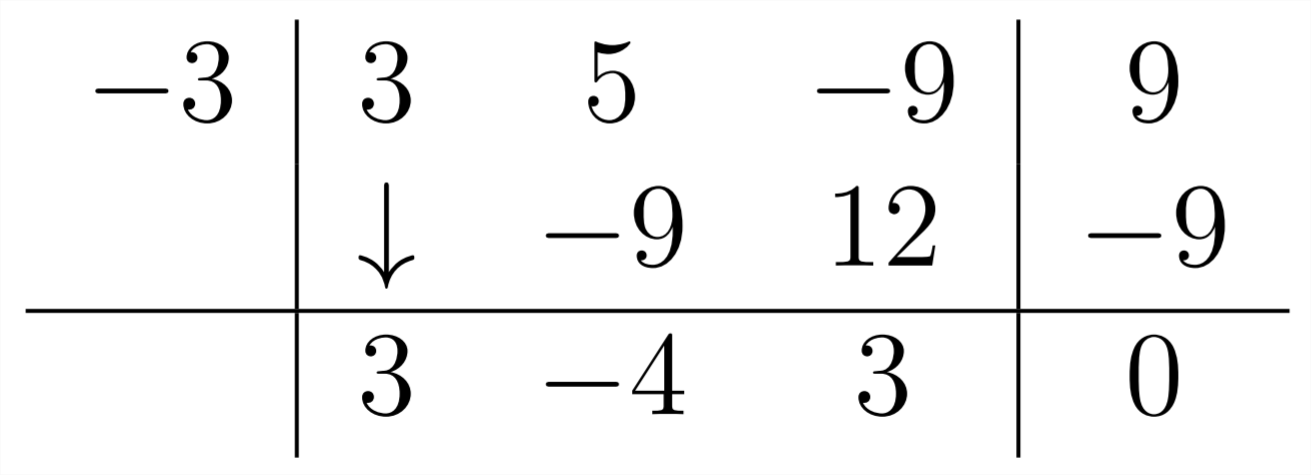
The answer here is $3 x^{2}-4 x+3$
$$\frac{3 x^{3}+5 x^{2}-9 x+9}{x+3}=3 x^{2}-4 x+3$$
and
$$3 x^{3}+5 x^{2}-9 x+9=(x+3)\left(3 x^{2}-4 x+3\right)$$
Let's look at an example that is a little bit different.

Example
Use Synthetic Division to divide:
$\frac{6 x^{4}+x^{3}+9 x^{2}+x-2}{2 x+1}$
Synthetic Division is set up to handle problems in which we are dividing by $1 x-a .$ Clearly, this is not the case in this example, however we can work around this. Another way of looking at setting up the synthetic division is that we use the number that is the solution to $x-a=0 .$ When we divided by $x-5,$ we used
+5. When we were dividing by $x+3$, we used $-3 .$ So, if we're going to divide by $2 x+1,$ we'll use $-\frac{1}{2}$ in the Synthetic Division:

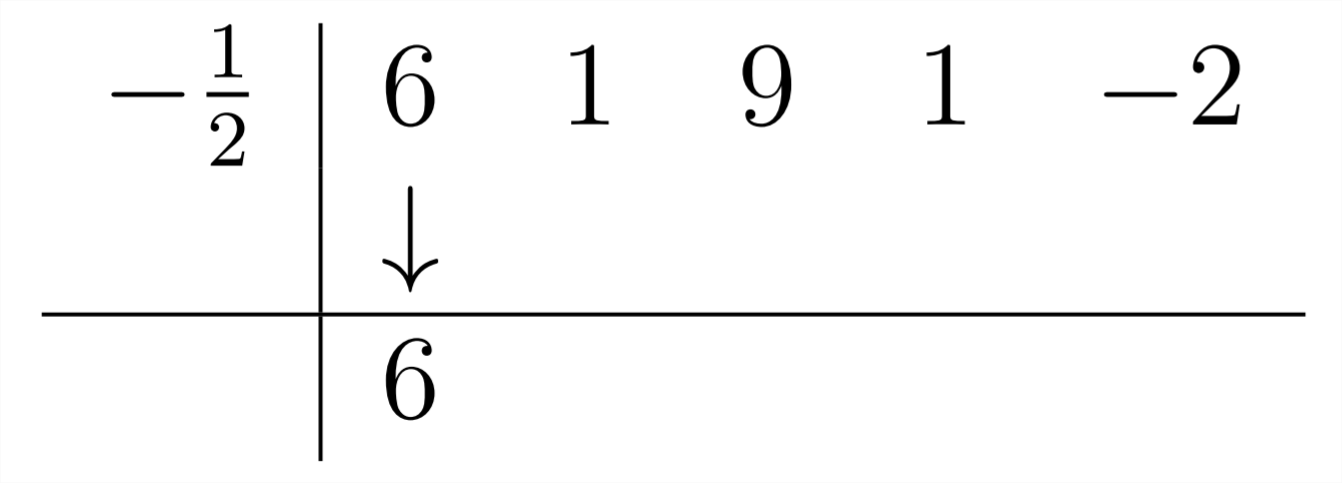
Then, we proceed as usual:

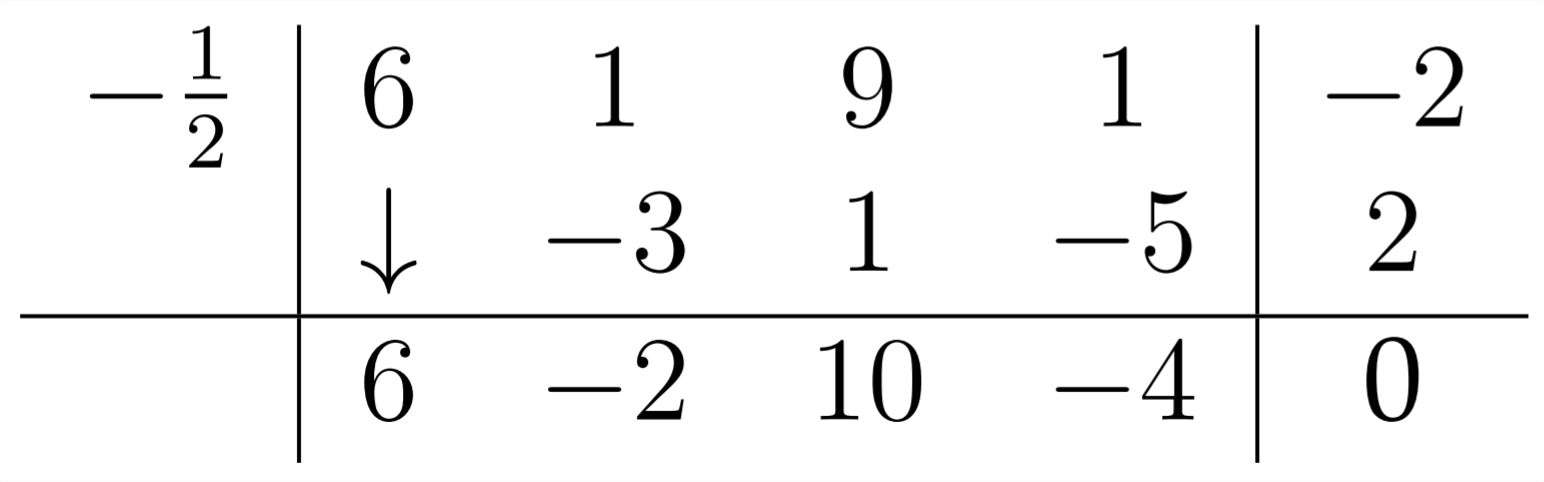
Notice that, again, we have a zero remainder. Also, notice that each coefficient in our answer has a common factor of $2,$ which was the coefficient of the $x$ in $2 x+1,$ which we originally were going to divide by. What we've done here is not division by $2 x+1,$ but division by $x+\frac{1}{2}$
So, in the end, our work tells us that:
$$\frac{6 x^{4}+x^{3}+9 x^{2}+x-2}{x+\frac{1}{2}}=6 x^{3}-2 x^{2}+10 x-4$$
and
$$6 x^{4}+x^{3}+9 x^{2}+x-2=\left(x+\frac{1}{2}\right)\left(6 x^{3}-2 x^{2}+10 x-4\right)$$
Notice that if we factor out the common factor of 2 from our answer, we can multiply it back into the $x+\frac{1}{2}$ and get an answer for our original problem:
$$\begin{aligned} 6 x^{4}+x^{3}+9 x^{2}+x-2 &=\left(x+\frac{1}{2}\right) 2\left(3 x^{3}-x^{2}+5 x-2\right) \\ &=(2 x+1)\left(3 x^{3}-x^{2}+5 x-2\right) \end{aligned}$$
This means that:
$$\frac{6 x^{4}+x^{3}+9 x^{2}+x-2}{2 x+1}=3 x^{3}-x^{2}+5 x-2$$
Another thing to understand about Synthetic Division is that if there is a missing power of $x$, then you should include a zero as the coefficient of that power

Example
Use Synthetic Division to divide:
$\frac{x^{3}+4 x-6}{x-2}$
since there is no $x^{2}$ term in the polynomial we're divding into, we'll enter a zero as the coefficient for that term:

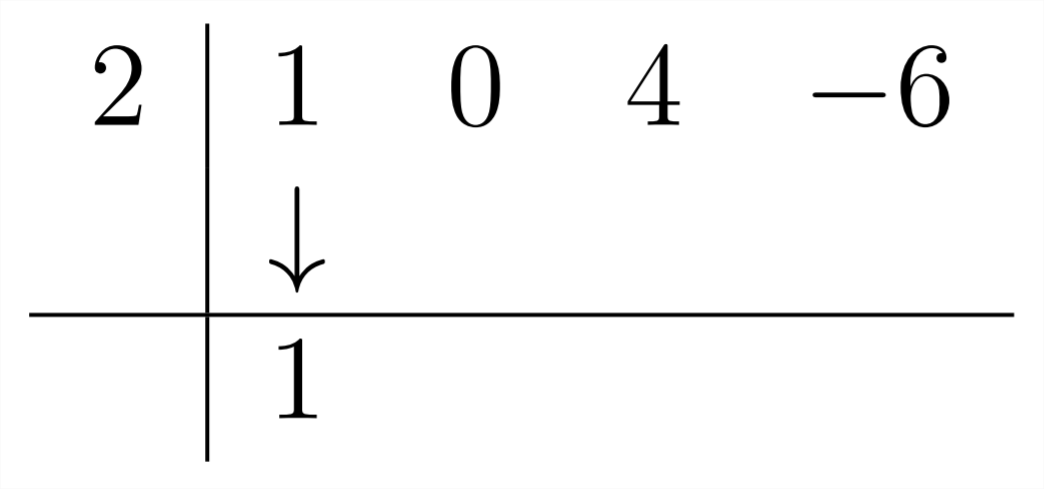
And then proceed as usual:

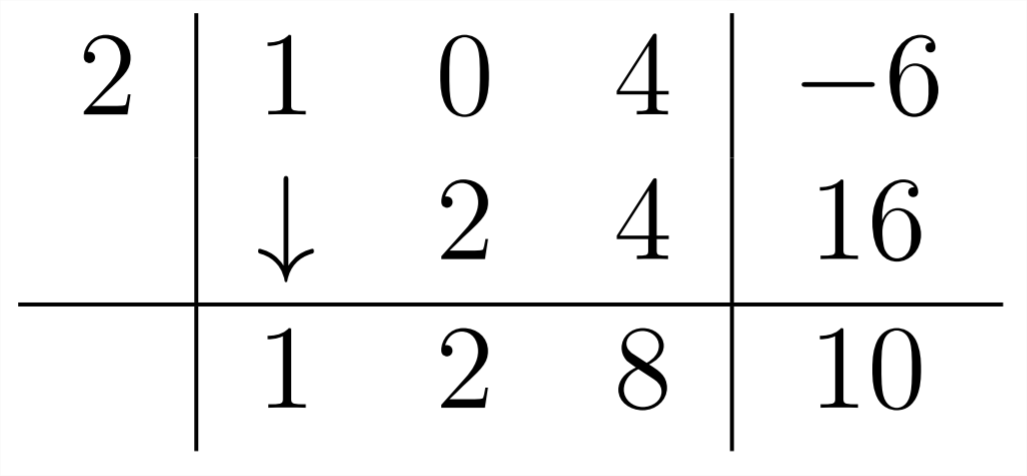
So the answer for this problem is $x^{2}+2 x+8$

Exercises 2.7
Use synthetic division to find the quotient in each problem.
1) $\frac{x^{3}-8 x^{2}+5 x+50}{x-5}$
2) $\frac{x^{3}+5 x^{2}-x-14}{x+2}$
3) $\frac{x^{3}+12 x^{2}+34 x-7}{x+7}$
4) $\frac{x^{3}-10 x^{2}+23 x-6}{x-3}$
5) $\frac{x^{4}-15 x^{2}+10 x+24}{x+4}$
6) $\frac{x^{4}-3 x^{3}+4 x^{2}-36}{x-3}$
7) $\frac{x^{4}-2 x^{3}-x+10}{x-2}$
8) $\frac{x^{4}-16 x^{2}-5 x-24}{x+4}$
9) $\frac{2 x^{4}-x^{3}+2 x-1}{2 x-1}$
10) $\frac{3 x^{4}+x^{3}-3 x+1}{3 x+1}$
11) $\frac{3 x^{4}-8 x^{3}+9 x^{2}-2 x-2}{3 x+1}$
12) $\frac{6 x^{4}-7 x^{3}+5 x^{2}-17 x+10}{3 x-2}$
13) $\frac{2 x^{3}+7 x^{2}+6 x-5}{2 x-1}$
14) $\frac{3 x^{4}-x^{3}-21 x^{2}-11 x+6}{3 x-1}$