5.5: Dividing Polynomials
- Page ID
- 5149
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Divide monomials
- Divide a polynomial by a monomial
- Divide polynomials using long division
- Divide polynomials using synthetic division
- Divide polynomial functions
- Use the remainder and factor theorems
Before you get started, take this readiness quiz.
Dividing Monomials
We are now familiar with all the properties of exponents and used them to multiply polynomials. Next, we’ll use these properties to divide monomials and polynomials.
Find the quotient: \(54a^2b^3÷ (−6ab^5)\).
Solution
When we divide monomials with more than one variable, we write one fraction for each variable.
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
Find the quotient: \(−72a^7b^3÷(8a^{12}b^4)\).
- Answer
-
\(−\dfrac{9}{a^5b}\)
Find the quotient: \(−63c^8d^3÷(7c^{12}d^2)\).
- Answer
-
\(\dfrac{−9d}{c^4}\)
Once you become familiar with the process and have practiced it step by step several times, you may be able to simplify a fraction in one step.
Find the quotient: \(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
Solution
Be very careful to simplify \(\dfrac{14}{21}\) by dividing out a common factor, and to simplify the variables by subtracting their exponents.
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
Find the quotient: \(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- Answer
-
\(\dfrac{4y^2}{7x^4}\)
Find the quotient: \(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- Answer
-
\(\dfrac{5}{8m^5n^3}\)
Divide a Polynomial by a Monomial
Now that we know how to divide a monomial by a monomial, the next procedure is to divide a polynomial of two or more terms by a monomial. The method we’ll use to divide a polynomial by a monomial is based on the properties of fraction addition. So we’ll start with an example to review fraction addition. The sum \(\dfrac{y}{5}+\dfrac{2}{5}\) simplifies to \(\dfrac{y+2}{5}\). Now we will do this in reverse to split a single fraction into separate fractions. For example, \(\dfrac{y+2}{5}\) can be written \(\dfrac{y}{5}+\dfrac{2}{5}\).
This is the “reverse” of fraction addition and it states that if a, b, and c are numbers where \(c\neq 0\), then \(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). We will use this to divide polynomials by monomials.
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Find the quotient: \((18x^3y−36xy^2)÷(−3xy)\).
Solution
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
Find the quotient: \((32a^2b−16ab^2)÷(−8ab)\).
- Answer
-
\(−4a+2b\)
Find the quotient: \((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- Answer
-
\(8a^5b+6a^3b^2\)
Divide Polynomials Using Long Division
Divide a polynomial by a binomial, we follow a procedure very similar to long division of numbers. So let’s look carefully the steps we take when we divide a 3-digit number, 875, by a 2-digit number, 25.
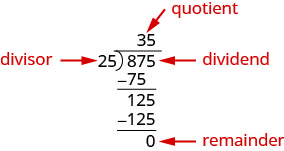
We check division by multiplying the quotient by the divisor. If we did the division correctly, the product should equal the dividend.
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
Now we will divide a trinomial by a binomial. As you read through the example, notice how similar the steps are to the numerical example above.
Find the quotient: \((x^2+9x+20)÷(x+5)\).
Solution
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| Write it as a long division problem. Be sure the dividend is in standard form. |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
Divide \(x^2\) by \(x\). It may help to ask yourself, “What do I need |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| Put the answer, \(x\), in the quotient over the \(x\) term. Multiply \(x\) times \(x+5\). Line up the like terms under the dividend. |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| Subtract \(x^2+5x\) from \(x^2+9x\). You may find it easier to change the signs and then add. Then bring down the last term, \(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
Divide \(4x\) by \(x\). It may help to ask yourself, “What do I need to multiply \(x\) by to get \(4x\)?” Put the answer, \(4\), in the quotient over the constant term. |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| Multiply 4 times \(x+5\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| Subtract \(4x+20\) from \(4x+20\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
Check: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
Find the quotient: \((y^2+10y+21)÷(y+3)\).
- Answer
-
\(y+7\)
Find the quotient: \((m^2+9m+20)÷(m+4)\).
- Answer
-
\(m+5\)
When we divided 875 by 25, we had no remainder. But sometimes division of numbers does leave a remainder. The same is true when we divide polynomials. In the next example, we’ll have a division that leaves a remainder. We write the remainder as a fraction with the divisor as the denominator.
Look back at the dividends in previous examples. The terms were written in descending order of degrees, and there were no missing degrees. The dividend in this example will be \(x^4−x^2+5x−6\). It is missing an \(x^3\) term. We will add in \(0x^3\) as a placeholder.
Find the quotient: \((x^4−x^2+5x−6)÷(x+2)\).
Solution
Notice that there is no \(x^3\) term in the dividend. We will add \(0x^3\) as a placeholder.
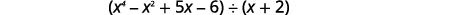 |
|
| Write it as a long division problem. Be sure the dividend is in standard form with placeholders for missing terms. | 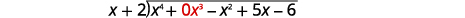 |
| Divide \(x^4\) by \(x\). Put the answer, \(x^3\), in the quotient over the \(x^3\) term. Multiply \(x^3\) times \(x+2\). Line up the like terms. Subtract and then bring down the next term. |
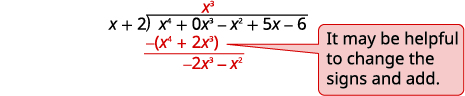 |
| Divide \(−2x^3\) by \(x\). Put the answer, \(−2x^2\), in the quotient over the \(x^2\) term. Multiply \(−2x^2\) times \(x+1\). Line up the like terms Subtract and bring down the next term. |
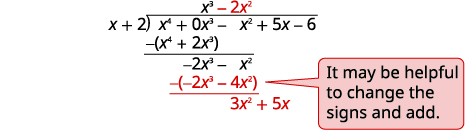 |
| Divide \(3x^2\) by \(x\). Put the answer, \(3x\), in the quotient over the \(x\) term. Multiply \(3x\) times \(x+1\). Line up the like terms. Subtract and bring down the next term. |
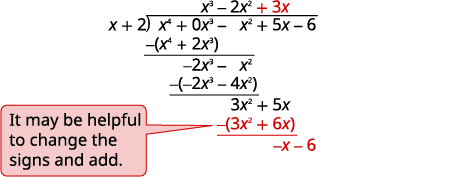 |
| Divide \(−x\) by \(x\). Put the answer, \(−1\), in the quotient over the constant term. Multiply \(−1\) times \(x+1\). Line up the like terms. Change the signs, add. Write the remainder as a fraction with the divisor as the denominator. |
 |
| To check, multiply \((x+2)(x^3−2x^2+3x−1−4x+2)\). The result should be \(x^4−x^2+5x−6\). |
Find the quotient: \((x^4−7x^2+7x+6)÷(x+3)\).
- Answer
-
\(x^3−3x^2+2x+1+3x+3\)
Find the quotient: \((x^4−11x^2−7x−6)÷(x+3)\).
- Answer
-
\(x^3−3x^2−2x−1−3x+3\)
In the next example, we will divide by \(2a−3\). As we divide, we will have to consider the constants as well as the variables.
Find the quotient: \((8a^3+27)÷(2a+3)\).
Solution
This time we will show the division all in one step. We need to add two placeholders in order to divide.
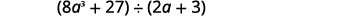 |
|
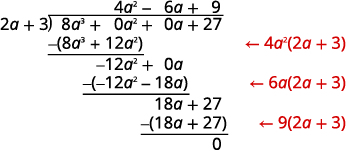 |
To check, multiply \((2a+3)(4a^2−6a+9)\).
The result should be \(8a^3+27\).
Find the quotient: \((x^3−64)÷(x−4)\).
- Answer
-
\(x^2+4x+16\)
Find the quotient: \((125x^3−8)÷(5x−2)\).
- Answer
-
\(25x^2+10x+4\)
Divide Polynomials using Synthetic Division
As we have mentioned before, mathematicians like to find patterns to make their work easier. Since long division can be tedious, let’s look back at the long division we did in Example and look for some patterns. We will use this as a basis for what is called synthetic division. The same problem in the synthetic division format is shown next.
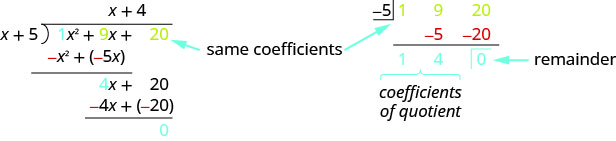
Synthetic division basically just removes unnecessary repeated variables and numbers. Here all the \(x\) and \(x^2\) are removed. as well as the \(−x^2\) and \(−4x\) as they are opposite the term above.
- The first row of the synthetic division is the coefficients of the dividend. The \(−5\) is the opposite of the 5 in the divisor.
- The second row of the synthetic division are the numbers shown in red in the division problem.
- The third row of the synthetic division are the numbers shown in blue in the division problem.
Notice the quotient and remainder are shown in the third row.
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
The following example will explain the process.
Use synthetic division to find the quotient and remainder when \(2x^3+3x^2+x+8\) is divided by \(x+2\).
Solution
| Write the dividend with decreasing powers of \(x\). | 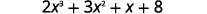 |
| Write the coefficients of the terms as the first row of the synthetic division. |
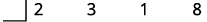 |
| Write the divisor as \(x−c\) and place c in the synthetic division in the divisor box. |
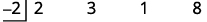 |
| Bring down the first coefficient to the third row. | 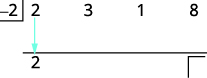 |
| Multiply that coefficient by the divisor and place the result in the second row under the second coefficient. |
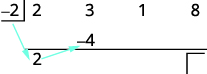 |
| Add the second column, putting the result in the third row. | 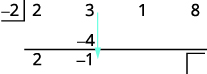 |
| Multiply that result by the divisor and place the result in the second row under the third coefficient. |
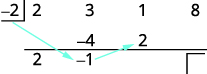 |
| Add the third column, putting the result in the third row. | 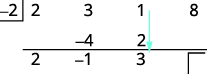 |
| Multiply that result by the divisor and place the result in the third row under the third coefficient. |
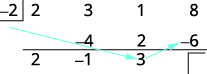 |
| Add the final column, putting the result in the third row. | 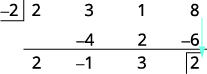 |
| The quotient is \(2x^2−1x+3\) and the remainder is 2. |
The division is complete. The numbers in the third row give us the result. The \(2\space\space\space−1\space\space\space3\) are the coefficients of the quotient. The quotient is \(2x^2−1x+3\). The 2 in the box in the third row is the remainder.
Check:
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
Use synthetic division to find the quotient and remainder when \(3x^3+10x^2+6x−2\) is divided by \(x+2\).
- Answer
-
\(3x^2+4x−2;\space 2\)
Use synthetic division to find the quotient and remainder when \(4x^3+5x^2−5x+3\) is divided by \(x+2\).
- Answer
-
\(4x^2−3x+1; 1\)
In the next example, we will do all the steps together.
Use synthetic division to find the quotient and remainder when \(x^4−16x^2+3x+12\) is divided by \(x+4\).
Solution
The polynomial \(x^4−16x^2+3x+12\) has its term in order with descending degree but we notice there is no \(x^3\) term. We will add a 0 as a placeholder for the \(x^3\) term. In \(x−c\) form, the divisor is \(x−(−4)\).
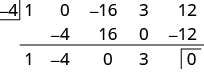
We divided a \(4^{\text{th}}\) degree polynomial by a \(1^{\text{st}}\) degree polynomial so the quotient will be a \(3^{\text{rd}}\) degree polynomial.
Reading from the third row, the quotient has the coefficients \(1\space\space\space−4\space\space\space0\space\space\space3\), which is \(x^3−4x^2+3\). The remainder
is 0.
Use synthetic division to find the quotient and remainder when \(x^4−16x^2+5x+20\) is divided by \(x+4\).
- Answer
-
\(x^3−4x^2+5;\space 0\)
Use synthetic division to find the quotient and remainder when \(x^4−9x^2+2x+6\) is divided by \(x+3\).
- Answer
-
\(x^3−3x^2+2;\space 0\)
Divide Polynomial Functions
Just as polynomials can be divided, polynomial functions can also be divided.
For functions \(f(x)\) and \(g(x)\), where \(g(x)\neq 0\),
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
For functions \(f(x)=x^2−5x−14\) and \(g(x)=x+2\), find:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\).
Solution
ⓐ
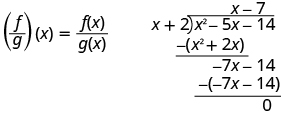
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ In part ⓐ we found \(\left(\dfrac{f}{g}\right)(x)\) and now are asked to find \(\left(\dfrac{f}{g}\right)(−4)\).
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
For functions \(f(x)=x^2−5x−24\) and \(g(x)=x+3\), find:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\).
- Answer a
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- Answer b
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
For functions \(f(x)=x2−5x−36\) and \(g(x)=x+4\), find:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\).
- Answer a
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- Answer b
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
Use the Remainder and Factor Theorem
Let’s look at the division problems we have just worked that ended up with a remainder. They are summarized in the chart below. If we take the dividend from each division problem and use it to define a function, we get the functions shown in the chart. When the divisor is written as \(x−c\), the value of the function at \(c\), \(f(c)\), is the same as the remainder from the division problem.
| Dividend | Divisor \(x−c\) | Remainder | Function | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \(−4\) |
| \(3x^3−2x^2−10x+8\) | \(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | 4 |
| \(x^4−16x^2+3x+15\) | \(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | 3 |
To see this more generally, we realize we can check a division problem by multiplying the quotient times the divisor and add the remainder. In function notation we could say, to get the dividend \(f(x)\), we multiply the quotient, \(q(x)\) times the divisor, \(x−c\), and add the remainder, \(r\).
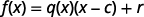 |
|
| If we evaluate this at \(c\), we get: | 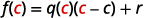 |
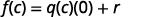 |
|
 |
This leads us to the Remainder Theorem.
If the polynomial function \(f(x)\) is divided by \(x−c\), then the remainder is \(f(c)\).
Use the Remainder Theorem to find the remainder when \(f(x)=x^3+3x+19\) is divided by \(x+2\).
Solution
To use the Remainder Theorem, we must use the divisor in the \(x−c\) form. We can write the divisor \(x+2\) as \(x−(−2)\). So, our \(c\) is \(−2\).
To find the remainder, we evaluate \(f(c)\) which is \(f(−2)\).
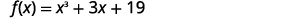 |
|
| To evaluate \(f(−2)\), substitute \(x=−2\). | 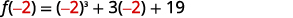 |
| Simplify. | 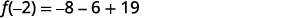 |
 |
|
| The remainder is 5 when \(f(x)=x^3+3x+19\) is divided by \(x+2\). | |
| Check: Use synthetic division to check. |
|
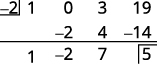 |
|
| The remainder is 5. |
Use the Remainder Theorem to find the remainder when \(f(x)=x^3+4x+15\) is divided by \(x+2\).
- Answer
-
\(−1\)
Use the Remainder Theorem to find the remainder when \(f(x)=x^3−7x+12\) is divided by \(x+3\).
- Answer
-
\(6\)
When we divided \(8a^3+27\) by \(2a+3\) in Example the result was \(4a^2−6a+9\). To check our work, we multiply \(4a2−6a+9\) by \(2a+3\) to get \(8a^3+27\).
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
Written this way, we can see that \(4a^2−6a+9\) and \(2a+3\) are factors of \(8a^3+27\). When we did the division, the remainder was zero.
Whenever a divisor, \(x−c\), divides a polynomial function, \(f(x)\), and resulting in a remainder of zero, we say \(x−c\) is a factor of \(f(x)\).
The reverse is also true. If \(x−c\) is a factor of \(f(x)\) then \(x−c\) will divide the polynomial function resulting in a remainder of zero.
We will state this in the Factor Theorem.
For any polynomial function \(f(x)\),
- if \(x−c\) is a factor of \(f(x)\), then \(f(c)=0\)
- if \(f(c)=0\), then \(x−c\) is a factor of \(f(x)\)
Use the Remainder Theorem to determine if \(x−4\) is a factor of \(f(x)=x^3−64\).
Solution
The Factor Theorem tells us that \(x−4\) is a factor of \(f(x)=x^3−64\) if \(f(4)=0\).
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
Since \(f(4)=0, x−4\) is a factor of \(f(x)=x^3−64\).
Use the Factor Theorem to determine if \(x−5\) is a factor of \(f(x)=x^3−125\).
- Answer
-
yes
Use the Factor Theorem to determine if \(x−6\) is a factor of \(f(x)=x^3−216\).
- Answer
-
yes
Access these online resources for additional instruction and practice with dividing polynomials.
- Dividing a Polynomial by a Binomial
- Synthetic Division & Remainder Theorem
Key Concepts
- Division of a Polynomial by a Monomial
- To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
- Division of Polynomial Functions
- For functions \(f(x)\) and \(g(x)\), where \(g(x)\neq 0\),
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- For functions \(f(x)\) and \(g(x)\), where \(g(x)\neq 0\),
- Remainder Theorem
- If the polynomial function \(f(x)\) is divided by \(x−c\), then the remainder is \(f(c)\).
- Factor Theorem: For any polynomial function \(f(x)\),
- if \(x−c\) is a factor of \(f(x)\), then \(f(c)=0\)
- if \(f(c)=0\), then \(x−c\) is a factor of \(f(x)\)


