2.6: Polynomial Long Division

Polynomial long division has many similarities to numerical long division, so it is important that we understand how and why numerical long division works the way it does before discussing polynomial long division. First the HOW?

Given the numerical problem $87,462 \div 38$, the first step is to determine the highest place value in the answer.

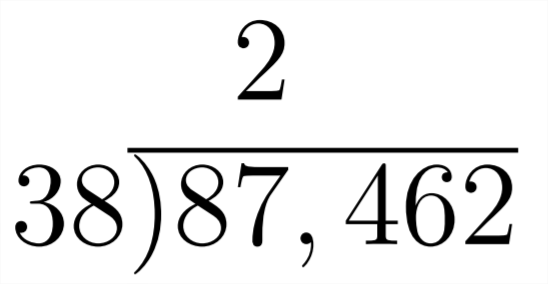
Often the first step in numerical long division is to say "Does 38 divide into $8 ? "$ "No." "Does 38 divide into $87 ? "$ "Yes." This tells us that the first digit in the answer will be over the 7 in $87,462,$ and consequently will be in the thousands place. Once we know that the first digit in the answer will be in the thousands place, the next question is "How many thousands?" We can determine that $2 *$ $38=76$ but $3 * 38=114$ (too big), so we know that the first digit in the answer will be $2 .$ Then we subtract, include the 4 and examine what is left over to continue.

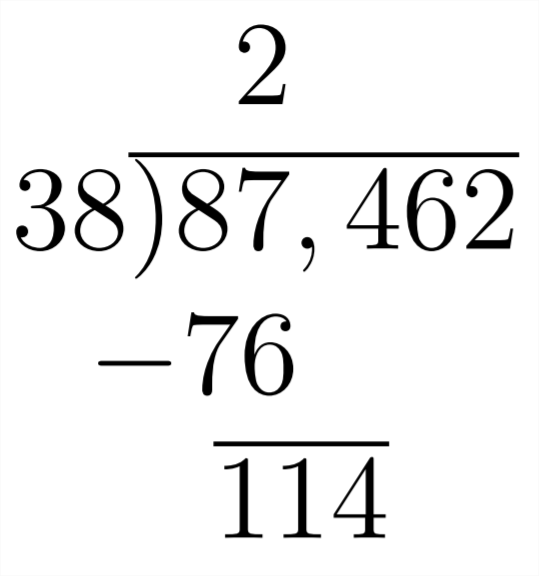
Here, we see that $114 \div 38=3$, so we know that the next digit in the answer will be 3

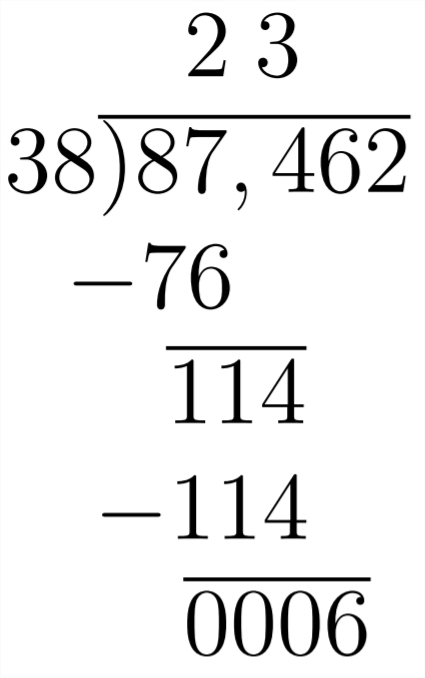
After including the $6,$ we can see that 38 does not divide evenly into $6,$ so we put a zero as the next digit in our answer and proceed:

Now that we have included all the digits from our original number $87,462,$ the last step is to divide 38 into $62 .$ This goes one time with 24 left over.

So, now we have the solution to the original problem $87,462 \div 38=2,301 \mathrm{R} 24$ or
$2,301 \frac{24}{38}$
The WHY? of the long division algorithm is somewhat hidden by the HOW? In the first step, we are determining which place value will hold the first digit of our answer. When we determine that 38 does divide into $87,$ this indicates that the first digit in our answer will be the thousands place. Dividing 38 into 87 tells us how many thousands there will be. Then we subtract:
$$\begin{array}{r} 87,462 \\ -76,000 \\ \hline 11,462 \end{array}$$

Now we need to determine how many times 38 will divide into $11,462 .$ We decided on $300 * 38=11,400,$ then we subtract to see how much is left over:
$$\begin{array}{r} 11,462 \\ -11,400 \\ \hline 00,062 \end{array}$$
We can see that we won't need any tens in our answer, and that 38 divides into 62 one time with 24 left over, thus the answer is 2 thousands, 3 hundreds, no tens, 1 and a remainder of $24 .$ To check the answer, we multiply $38 * 2301$ and add 24:
$$\begin{array}{c} 2,301 \\ \times 38 \\ \hline 18408 \\ 6903 \\ \hline 87438 \\ +24 \\ \hline 87462 \end{array}$$
Polynomial long division works in much the same way that numerical long division does. Given a problem $A \div B$, the goal is to find a quotient $Q$ and remainder $R$ so that $A=B * Q+R$
Let's look at this with the example $2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 \div x^{2}+3 x+1$ or:
$$\frac{2 x^{4}+7 x^{3}+4 x^{2}-2 x-1}{x^{2}+3 x+1}$$
So, we are looking to answer the question:
$$\begin{array}{cccccc} A & = & B & * & Q & +R \\ 2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 & = & \left(x^{2}+3 x+1\right) & * & (?+?+?) & +? \end{array}$$
If we want to mulitply $x^{2}+3 x+1$ times something and end up with $2 x^{4}+7 x^{3}+$ $4 x^{2}-2 x-1,$ then what we multiply by is going to have to start with $2 x^{2},$ because
$$x^{2} * 2 x^{2}=2 x^{4}$$

Now we're working with this:
$$\begin{array}{cccc} A & = & B & * & Q & +R \\ 2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 & = & \left(x^{2}+3 x+1\right) & * &\left(2 x^{2}+?+?\right) & +? \end{array}$$
But the $2 x^{2}$ doesn't just get multiplied by the $x^{2}$, it will also get multiplied by the $3 x$ and the $1 .$ So now we have:
$$\begin{array}{ccccc} A & = & B & * & Q & +R \\ 2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 & = & \left(x^{2}+3 x+1\right) & * &\left(2 x^{2}+?+?\right) & +? \\ & & =2 x^{4}+6 x^{3}+2 x^{2}+? ? ? ? ? \end{array}$$

The issue this raises is that the next multiplication $\left(? * x^{2}+? * 3 x+? * 1\right)$ needs to add only $1 x^{3}$ to our answer, because we need $7 x^{3}$ and we already have $6 x^{3}$ from the previous multiplication. That means we're going to want to multiply next by
$1 x:$
$$\begin{aligned} A &=\quad B \quad * \quad Q \quad+R \\ 2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 &=\left(x^{2}+3 x+1\right) *\left(2 x^{2}+1 x+?\right)+? \\ &=2 x^{4}+6 x^{3}+2 x^{2} \\ &=\quad 1 x^{3}+3 x^{2}+x \\ &=2 x^{4}+7 x^{3}+5 x^{2}+1 x+? ? ? \end{aligned}$$
In the next round of mutiplication, we're going to want to bring the $5 x^{2}$ down to $4 x^{2},$ so we'll need to multiply by -1

$$\begin{aligned} A &=\quad B \quad * \quad Q \quad+R \\ 2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 &=\left(x^{2}+3 x+1\right) *\left(2 x^{2}+1 x-1\right)+0 \\ &=2 x^{4}+6 x^{3}+2 x^{2} \\ &=\quad 1 x^{3}+3 x^{2}+x \\ &=\quad \quad-1 x^{2}-3 x-1 \\ &=2 x^{4}+7 x^{3}+5 x^{2}-2 x-1 \end{aligned}$$
Now we also know that the remainder is zero, because $x^{2}+3 x+1$ divides evenly into $2 x^{4}+7 x^{3}+4 x^{2}-2 x-1$ and so:
$$2 x^{4}+7 x^{3}+4 x^{2}-2 x-1=\left(x^{2}+3 x+1\right) *\left(2 x^{2}+1 x-1\right)$$
This method makes the reasoning behind dividing polynomials somewhat more apparent than the long division process, but it is more cumbersome. The way that polynomial long division is usually approached is as follows:

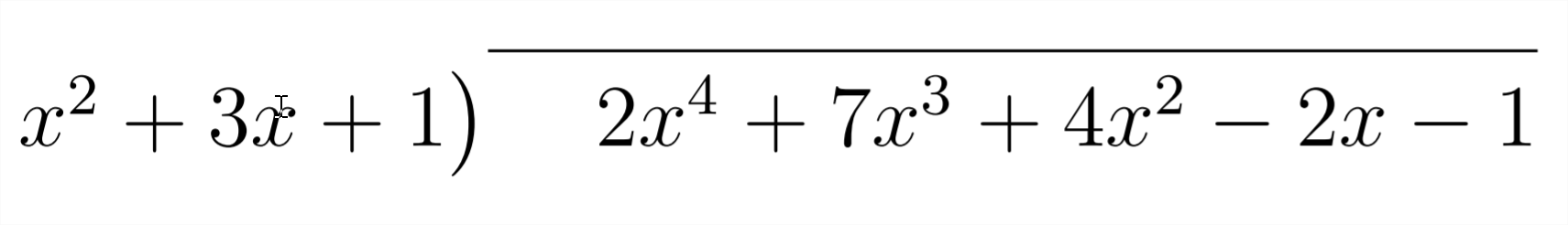
Then, just as we did in the other method, we question "What should we multiply $x^{2}$ by to get $2 x^{4} ?^{\prime \prime}$ Answer: $^{\prime \prime} 2 x^{2 \prime \prime}$ This is the first term in our answer:

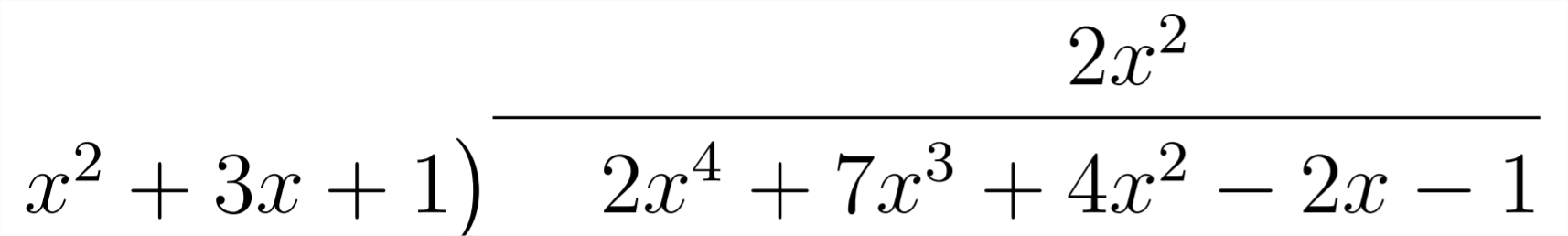
Then we multiply $2 x^{2}\left(x^{2}+3 x+1\right)$ and change all the signs to see what we'll be left with:

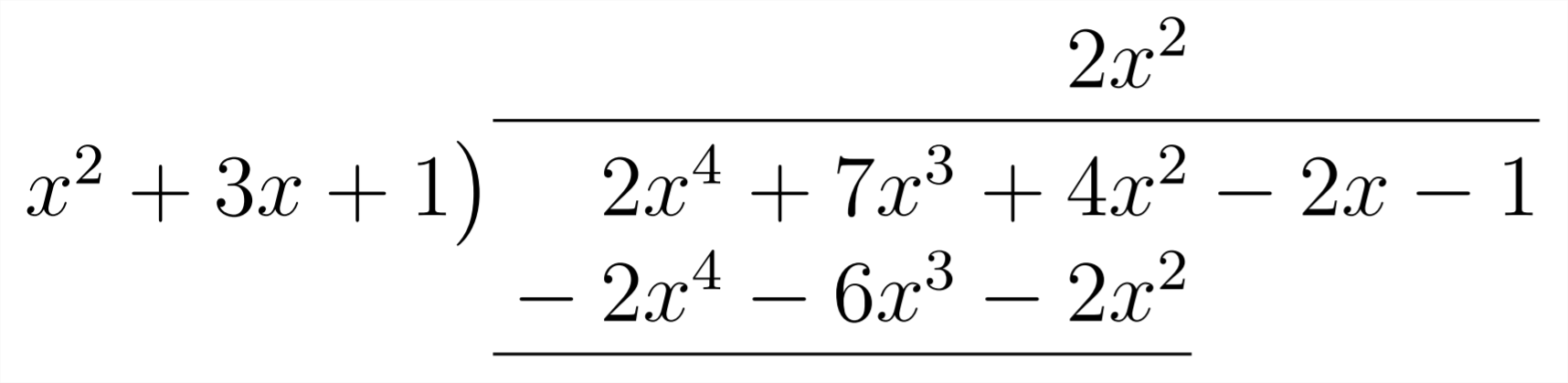
This indicates that we'll have the $2 x^{4}$ we'll need in our answer, as well six of the seven $x^{3}$ 's and two of the four $x^{2}$ 's. We'll now need $1 x^{3}$ next:

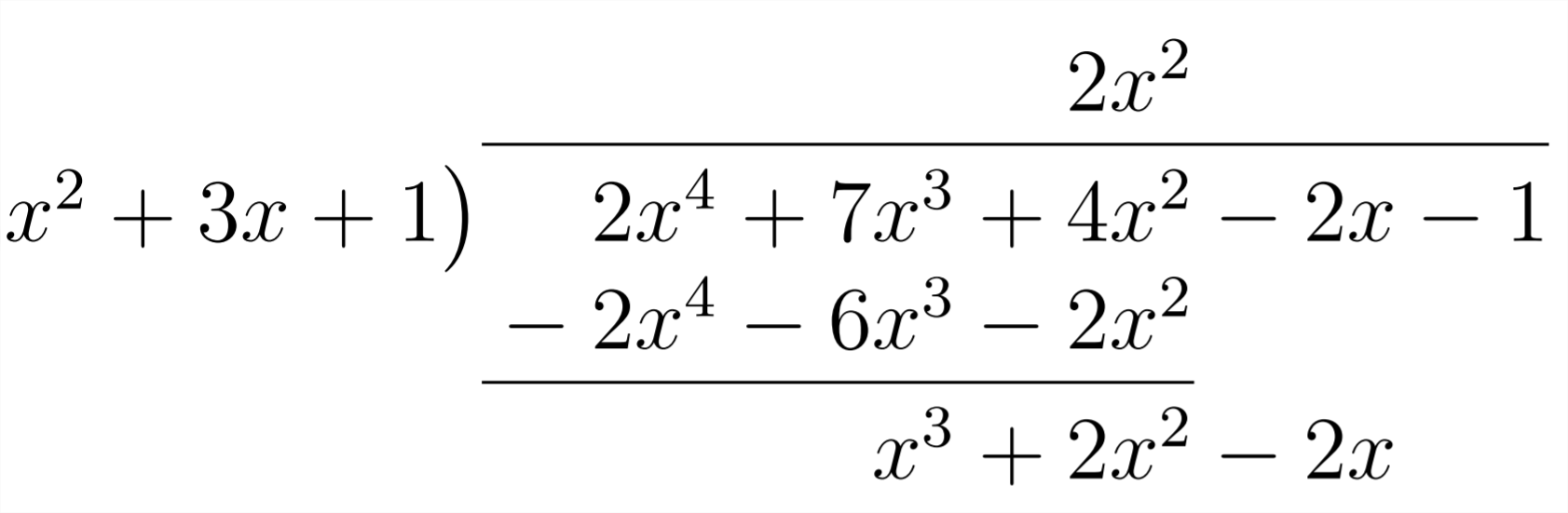
This means we'll need to multiply by $1 x$ :

Here, we still need to pick up a $-1 x^{2}$, which means that our next multiplication will be with -1:

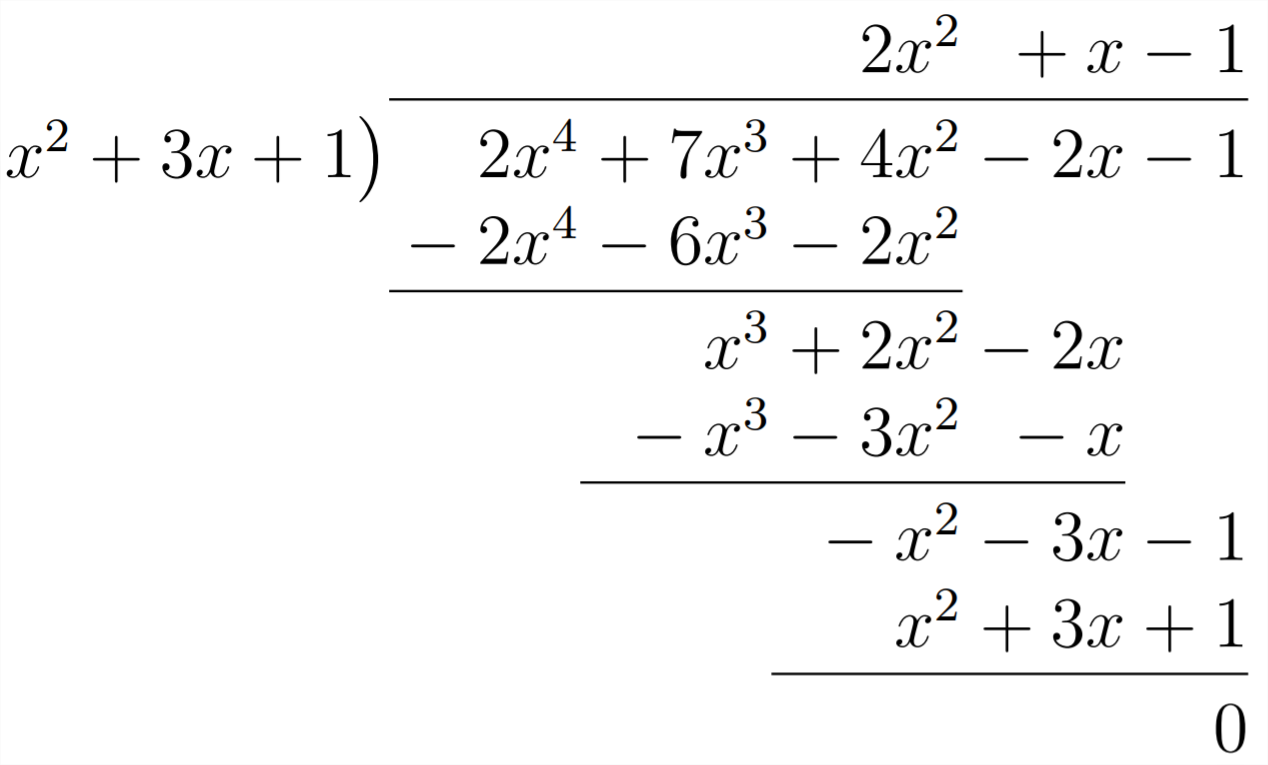
Because $x^{2}+3 x+1$ divides evenly into $2 x^{4}+7 x^{3}+4 x^{2}-2 x-1$ we have a zero remainder. In the next example there will be a non-zero remainder:

Example
Divide:
$\frac{3 x^{4}-8 x^{3}+19 x^{2}-15 x+10}{x^{2}-x+4}$

First, we set up the problem:

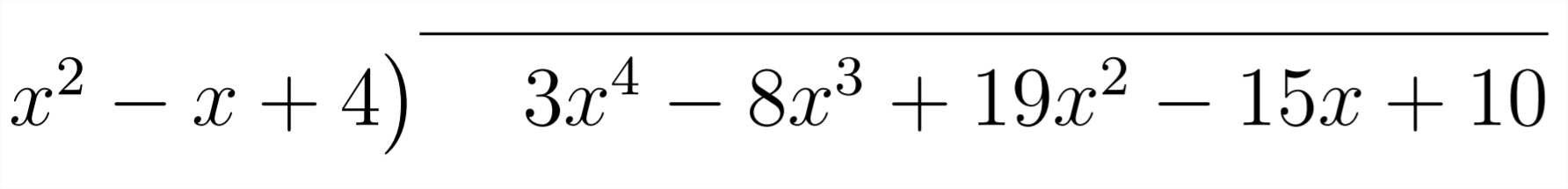
Then, we question: "What do we need to multiply $x^{2}$ by to get $3 x^{4} ? "$ Answer:

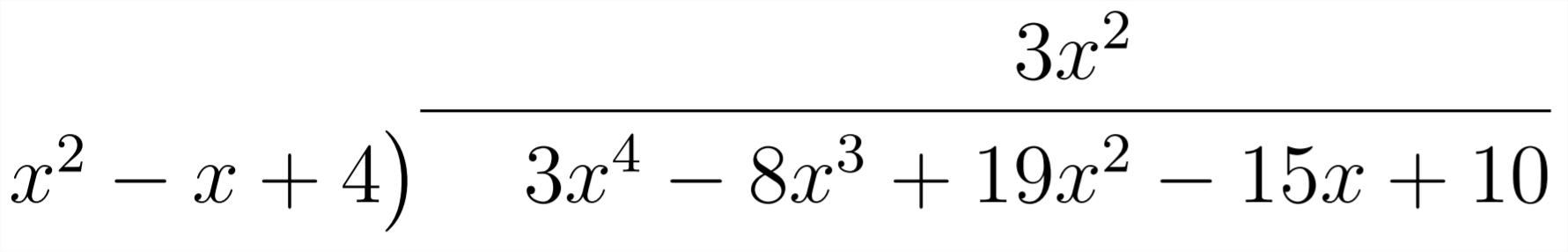
Then, we multiply, change signs (subtract) and combine like terms:

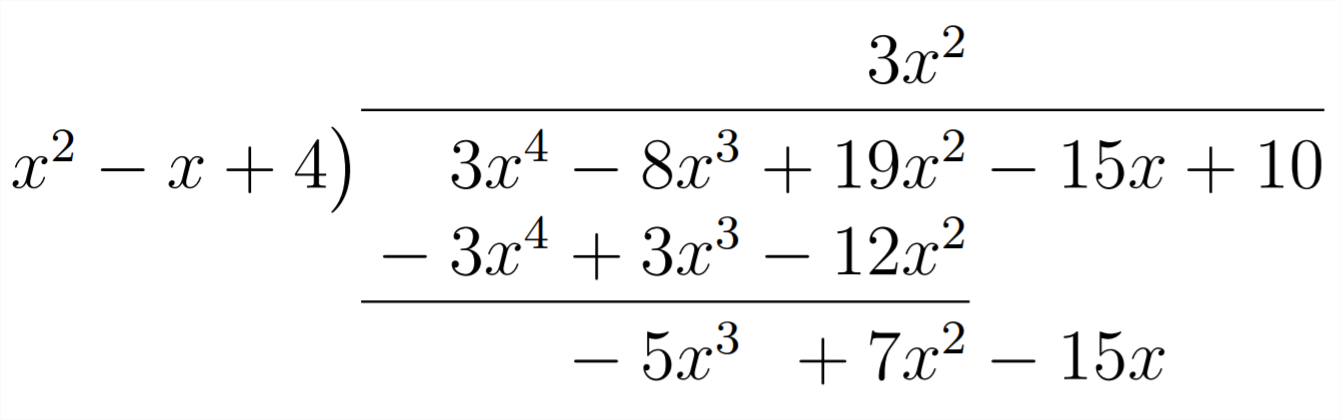
Now we'll need to multiply by $-5 x,$ change signs and combine like terms:

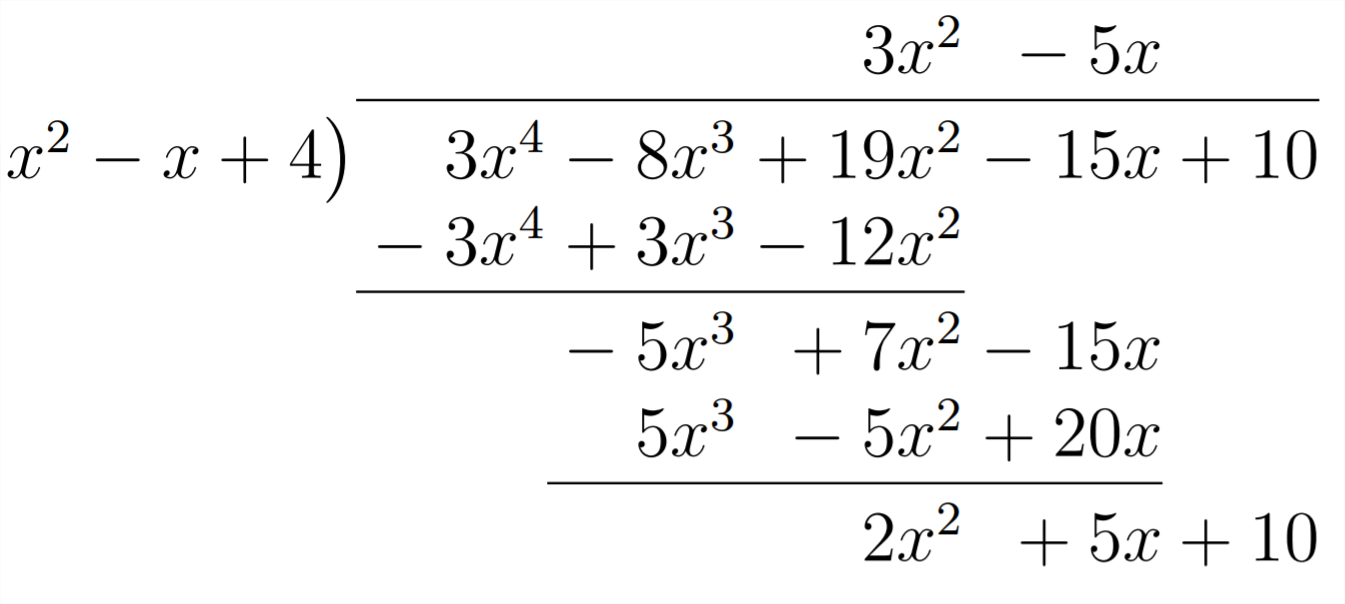
We need $2 x^{2}$ so we'll need to multiply by 2 , change signs and combine like terms:

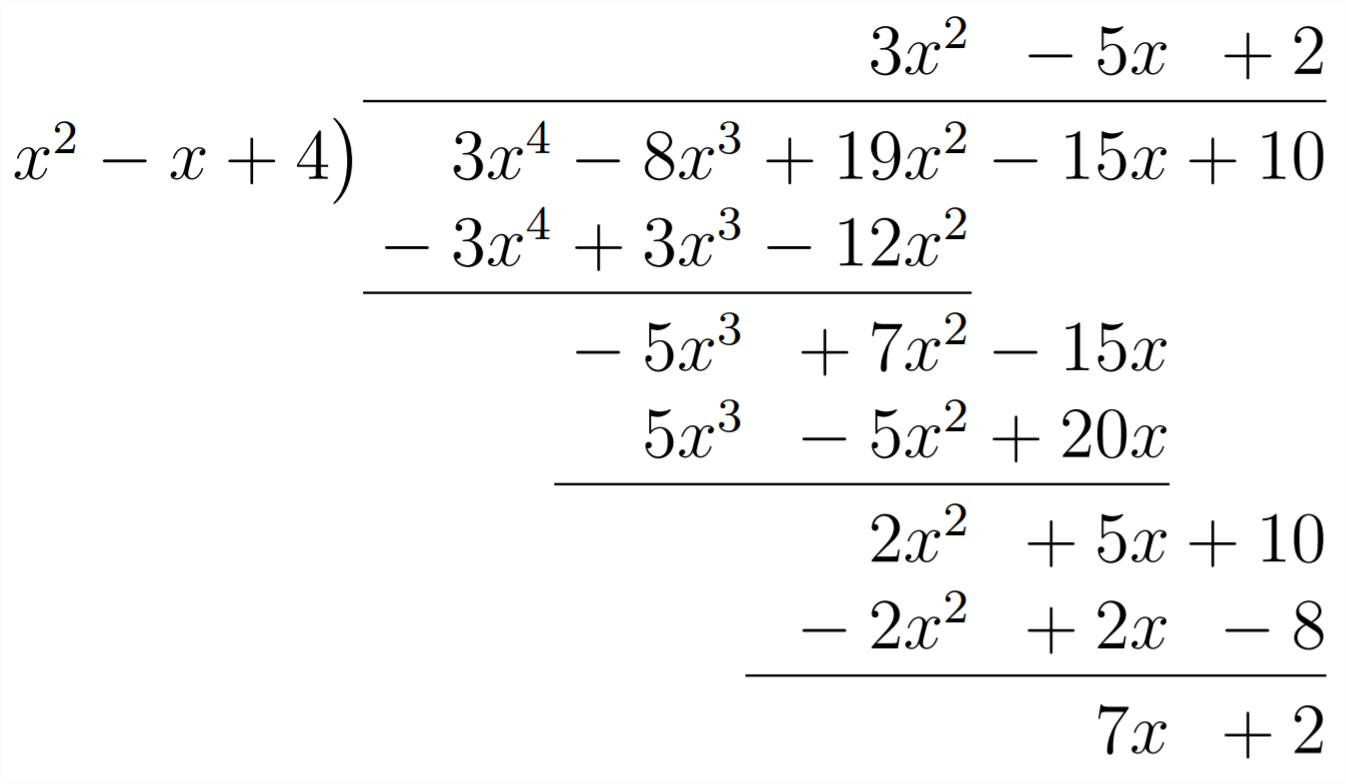
Because there is no positive power of $x$ that we can multiply $x^{2}$ by to get $7 x,$ then this is our remainder: $7 x+2$
So:
$$\begin{array}{ccccc} A & = & B & * & Q & + & R \\ 3 x^{4}-8 x^{3}+19 x^{2}-15 x+10 & =\left(x^{2}-x+4\right) & *\left(3 x^{2}-5 x+2\right) & +(7 x+2) \end{array}$$

Exercises 2.6
Find the quotient in each problem.
1) $\frac{y^{3}-4 y^{2}+6 y-4}{y-2}$
2) $\frac{x^{3}-5 x^{2}+x+15}{x-3}$
3) $\frac{x^{3}-4 x^{2}-3 x-10}{x^{2}+x+2}$
4) $\frac{2 x^{3}-3 x^{2}+7 x-3}{x^{2}-x+3}$
5) $\frac{x^{4}+2 x^{3}-x^{2}+x+6}{x+2}$
6) $\frac{x^{4}+x^{3}+5 x^{2}+3 x+6}{x^{2}+x-1}$
7) $\frac{2 z^{3}+5 z+8}{z+1}$
8) $\frac{x^{5}+3 x+2}{x^{3}+2 x+1}$
9) $\frac{x^{4}+2 x^{3}+4 x^{2}+3 x+2}{x^{2}+x+2}$
10) $\frac{2 x^{4}+3 x^{3}+3 x^{2}-5 x-3}{2 x^{2}-x-1}$
11) $\frac{2 y^{5}-3 y^{4}-y^{2}+y+4}{y^{2}+1}$
12) $\frac{3 x^{5}-4 x^{3}+3 x^{2}+12 x-10}{x^{2}+2 x-1}$
13) $\frac{5 x^{4}-3 x^{2}+2}{x^{2}-3 x+5}$
14) $\frac{3 y^{3}-4 y^{2}-3}{y^{2}+5 y+2}$