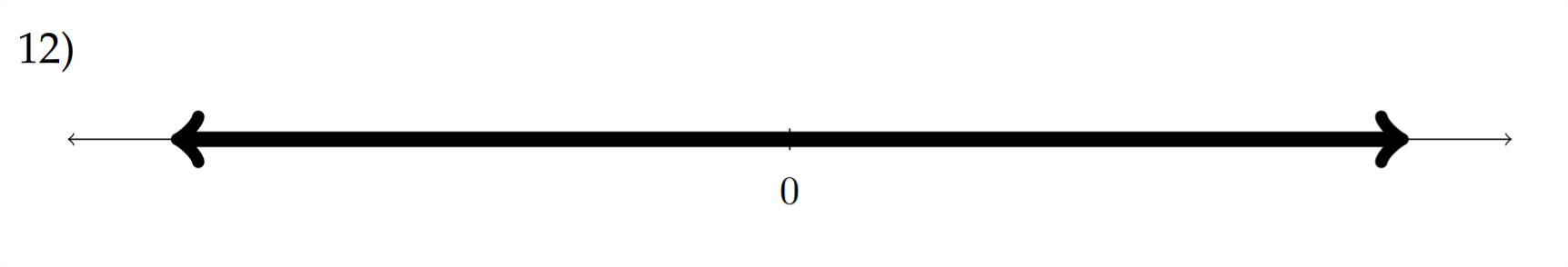Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

2.1: Representing Intervals

Last updated

Oct 6, 2021
Save as PDF
- 2: Polynomial and Rational Functions
- 2.2: Solution by Graphing

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Many of the problems in this chapter will have solutions that must be expressed as an interval. This means a range of $x$ values that will satisfy the original problem. In this section, we will introduce the translation of graphical intervals into algebraic notation.

For example, in the diagram below, we would represent the interval shown on the graph as $x<-3$
$clipboard_eb76b2b501253ec087968e0ded39f19b6.png$
In this diagram, we would represent the interval shown on the graph as $1 \leq x<7.$

$clipboard_e9efa308938eaa346bfad27ec84d88829.png$
In the next diagram, we have two separate intervals to represent-and we will need two separate statements to represent them.

$clipboard_e8fed7be98d4d66e0cb7e616ebe645aa5.png$

These intervals would be represented as $x<-4$ OR $x \geq 6$
Sometimes students try to represent the intervals above as $6 \leq x<-4,$ however, this expression would represent a single interval where $x$ is both less than -4 and, at the same time, greater than or equal to $+6 .$ This is simply not possible, and would result in the empty set, which is the reason that the OR portion is needed in the correct answer.

Example
Represent the intervals indicated on the graph below:
$clipboard_e26ab5d42b88bf8d9260ff320bdad4bd5.png$

On this graph, there is one interval beginning at -5 and ending at +5 and another beginning at 30 and continuing to infinity. Thus, these intervals would be represented as $-5<x \leq 5$ OR $x \geq 30$

Students familiar with another form of interval notation may wish to represent this interval as $(-5,5] \cup[30, \infty) .$ Both forms of notation accomplish the same goal.

Exercises 2.1
In each problem below, represent the intervals indicated on the graph.
$clipboard_e452461bbf43bd893d7a8b87268d77ace.png$
$clipboard_eb532daaae81f8f528f2df05b1e7800d8.png$
$clipboard_ea2aeaa0bab156cd72cf096bd2f9096b1.png$
$clipboard_e98775341b5bc61b0b304f91e98de8eee.png$
$clipboard_e3c65f63bd3e38a119b41afe2e2d733f9.png$
$clipboard_ec93850db0eb839f71c6d274aaa970048.png$
$clipboard_eea3931ba95a2f717c7a34d8dee8a8e6d.png$
$clipboard_e138a880820b4bea9e16905db2c0404fd.png$
$clipboard_e1812c88b1a01d3bd977d7f4926b31401.png$
$clipboard_e596c00f5214f342dbeef6f5b7149a10d.png$
$clipboard_e4a8a7e3d2d4cfcd8a70f86577b3d102a.png$
$clipboard_e3f292107a5d3729ec583e418bceb8137.png$
$clipboard_efbe30bc5e206154bf0ad833ace38c36f.png$
$clipboard_e94ca8c3f6cd1a7fc2c69a0a351ff7b4d.png$

Support Center

How can we help?