2.3: Solution of Polynomial Inequalities by Graphing

In this section, we will combine the concepts of the previous two sections to solve polynomial inequalities. In Section 2.2, we solved equations by graphing and finding the 𝑥 -values which made 𝑦 =0. In solving an inequality, we will be concerned with finding the range of 𝑥 values that make 𝑦 either greater than or less than 0, depending on the given problem.
Example
Solve the given inequality.
2⁢𝑥3 +8⁢𝑥2 +5⁢𝑥 −3 ≥0
First, we graph the function:

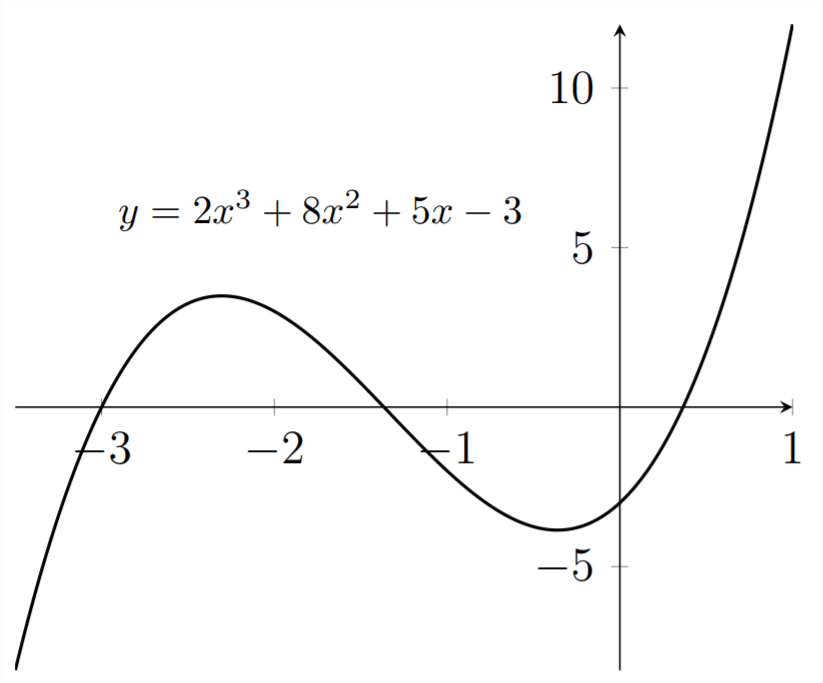
Then we identify the intervals of 𝑥 -values that make the 𝑦 value greater than or equal to zero, as indicated in the problem.

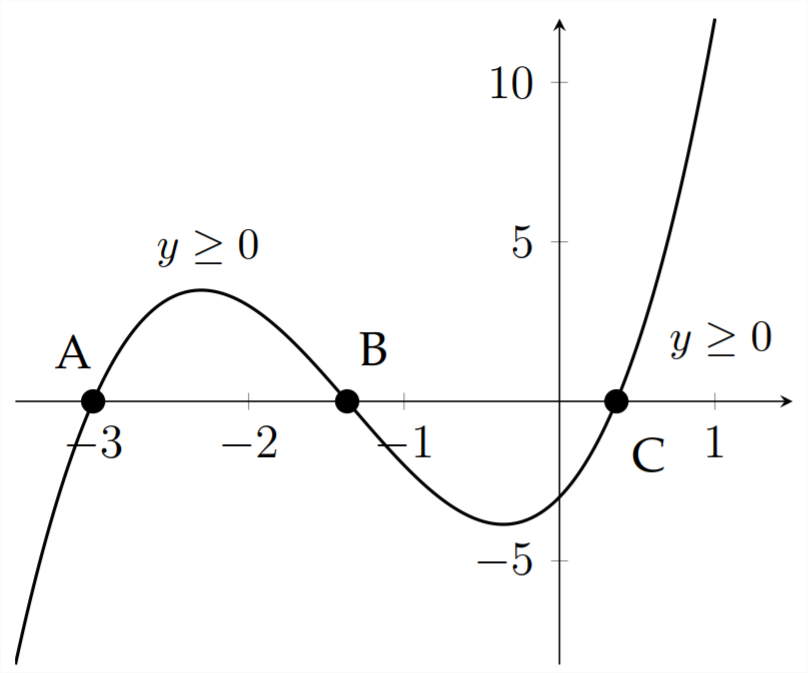
The indicated roots of the function (𝐴,𝐵 and 𝐶) are the 𝑥 -values that make 𝑦 equal to zero. These points divide the graph between the regions where 𝑦 is greater than zero and the regions where 𝑦 is less than zero. The solution to the given inequlaity 2⁢𝑥3 +8⁢𝑥2 +5⁢𝑥 −3 ≥0 are A ≤𝑥 ≤B OR 𝑥 ≥C
When we find the values of A,B and C :A =−3,B ≈−1.366 and C ≈0.366, we can
complete the solution to the problem.
2⁢𝑥3 +8⁢𝑥2 +5⁢𝑥 −3 ≥0
−3 ≤𝑥 ≤−1.366 OR 𝑥 ≥0.366

Example
Solve the given inequality.
𝑥4 −2⁢𝑥3 −5⁢𝑥2 +8⁢𝑥 +3 ≤0
First, we graph the function:

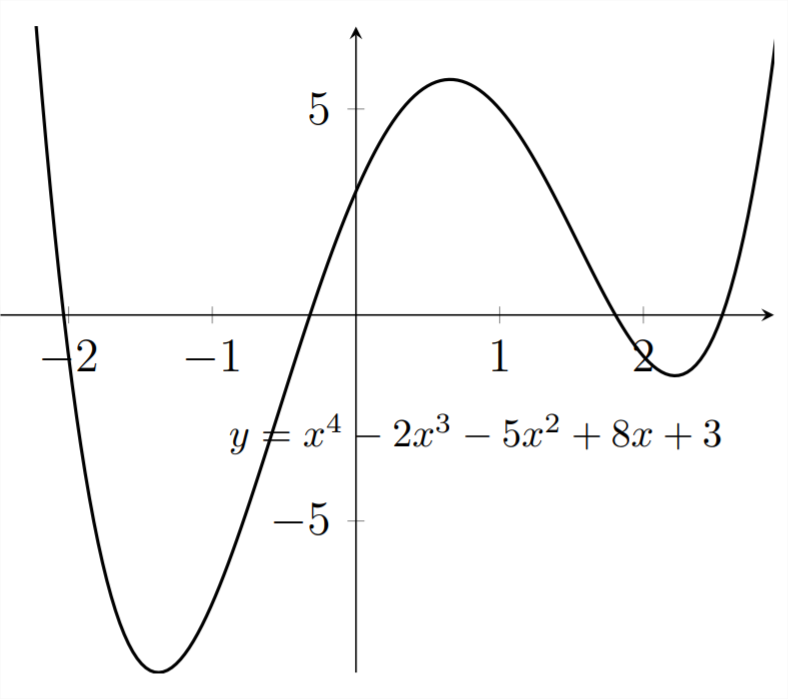
In this problem, we're looking for the intervals of 𝑥 values that make 𝑦 less than or equal to zero. First, we identify the roots of the function:

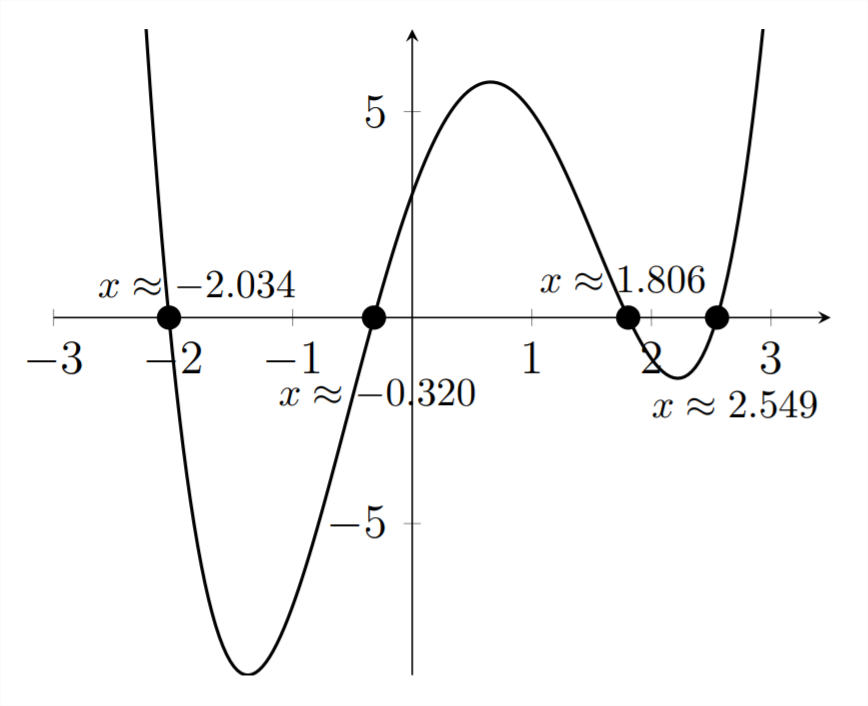
Next, we'll identify the intervals where the 𝑦 values are less than zero:

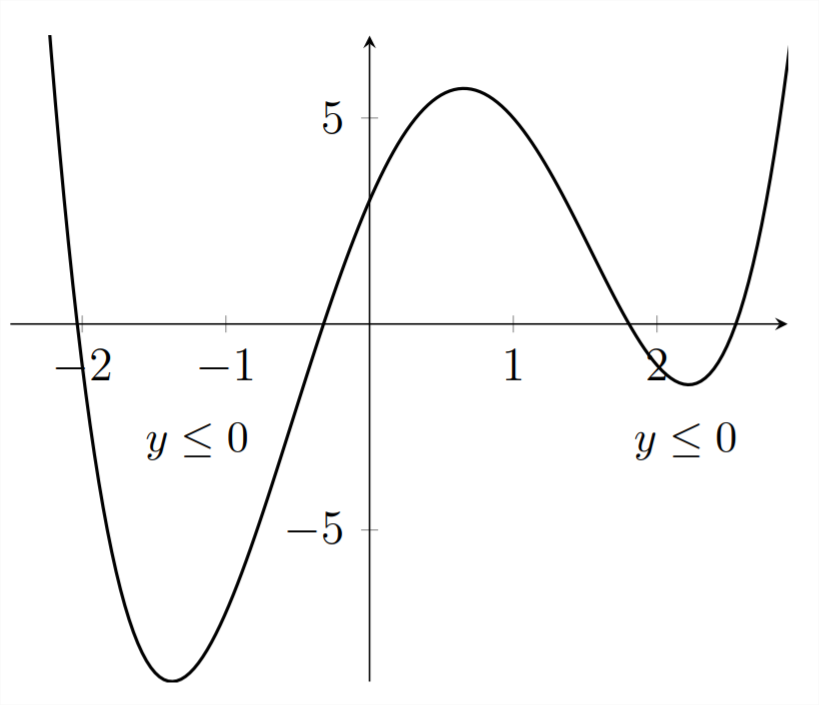
So, the solution to the original inequality is:
𝑥4 −2⁢𝑥3 −5⁢𝑥2 +8⁢𝑥 +3 ≤0
−2.034 ≤𝑥 ≤−0.320 OR 1.806 ≤𝑥 ≤2.549
In the next example we'll be looking to identify both the intervals where 𝑦 is greater than zero, and the intervals where 𝑦 is less than zero.

Example
Determine the interval(s) for which 𝑥3 +5⁢𝑥2 +5⁢𝑥 +1 ≥0
Determine the interval(s) for which 𝑥3 +5⁢𝑥2 +5⁢𝑥 +1 <0
Once again, we'll start by graphing the function to find the roots:

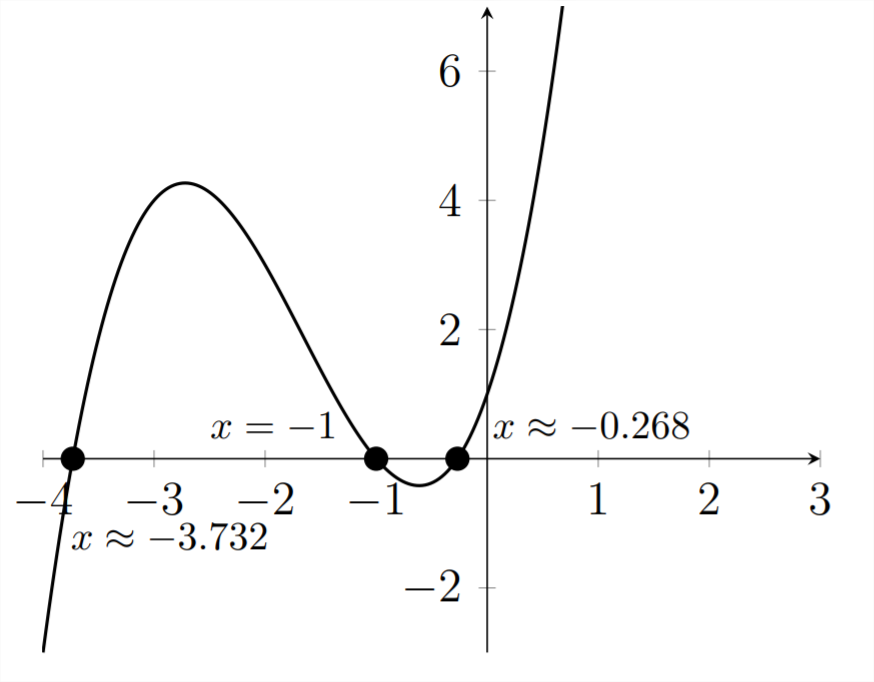
Now that we've indentified the roots, we can determine where the 𝑦 values are greater than zero and where they're less than zero.

For 𝑦 ≥0, we can see that this corresponds to: −3.732 ≤𝑥 ≤−1 OR 𝑥 ≥−0.268
For 𝑦 <0, we can see that this corresponds to: 𝑥 <−3.732⁢OR −1 <𝑥 <−0.268

Exercises 2.3
1) Determine the interval(s) for which 𝑥3 −4⁢𝑥2 +2⁢𝑥 +3 ≥0
Determine the interval(s) for which 𝑥3 −4⁢𝑥2 +2⁢𝑥 +3 <0
2) Determine the interval(s) for which 4⁢𝑥3 −4⁢𝑥2 −19⁢𝑥 +10 ≥0
Determine the interval(s) for which 4⁢𝑥3 −4⁢𝑥2 −19⁢𝑥 +10 <0
3) Determine the interval(s) for which 𝑥3 −2.5⁢𝑥2 −7⁢𝑥 −1.5 ≥0
Determine the interval(s) for which 𝑥3 −2.5⁢𝑥2 −7⁢𝑥 −1.5 <0
4) Determine the interval(s) for which 𝑥3 −3.5⁢𝑥2 +0.5⁢𝑥 +5 ≥0
Determine the interval(s) for which 𝑥3 −3.5⁢𝑥2 +0.5⁢𝑥 +5 <0
5) Determine the interval(s) for which 6⁢𝑥4 −13⁢𝑥3 +2⁢𝑥2 −4⁢𝑥 +15 ≥0
Determine the interval(s) for which 6⁢𝑥4 −13⁢𝑥3 +2⁢𝑥2 −4⁢𝑥 +15 <0
6) Determine the interval(s) for which 𝑥4 −𝑥3 −𝑥2 +3⁢𝑥 −5 ≥0
Determine the interval(s) for which 𝑥4 −𝑥3 −𝑥2 +3⁢𝑥 −5 <0
7) Determine the interval(s) for which 3⁢𝑥4 +3⁢𝑥3 −14⁢𝑥2 −𝑥 +3 ≥0
Determine the interval(s) for which 3⁢𝑥4 +3⁢𝑥3 −14⁢𝑥2 −𝑥 +3 <0
8) Determine the interval(s) for which 4⁢𝑥4 −4⁢𝑥3 −7⁢𝑥2 +4⁢𝑥 +3 ≥0
Determine the interval(s) for which 4⁢𝑥4 −4⁢𝑥3 −7⁢𝑥2 +4⁢𝑥 +3 <0

Determine the interval(s) that satisfy each inequality.
9) 𝑥3 +𝑥2 −5⁢𝑥 +3 ≤0
10) 𝑥3 −7⁢𝑥 +6 >0
11) 𝑥3 −13⁢𝑥 +12 >0
12) 𝑥4 −10⁢𝑥2 +9 <0
13) 6⁢𝑥4 −9⁢𝑥2 −4⁢𝑥 +12 ≥0
14) 𝑥4 −5⁢𝑥3 +20⁢𝑥 −16 >0
15) 𝑥3 −2⁢𝑥2 −7⁢𝑥 +6 ≤0
16) 𝑥4 −6⁢𝑥3 +2⁢𝑥2 −5⁢𝑥 +2 ≤0
17) 2⁢𝑥4 +3⁢𝑥3 −2⁢𝑥2 −4⁢𝑥 +2 >0
18) 𝑥5 +5⁢𝑥4 −4⁢𝑥3 +3⁢𝑥2 −2 ≤0