4.4: Transformations

There are three major types of transformation that we will consider:
1) Horizontal and vertical shifts
2) Reflections over the \(x\) or \(y\) -axis
3) Horizontal and vertical stretches
If we take a given function, let's say \(f(x)=x,\) then this has the graph we see below - a straight line with a slope of 1 and a \(y\) -intercept of \(0 .\) If we add to the function \(f(x)+6=x+6,\) then this will add 6 to all of the \(y\) -values which shifts the graph 6 places up.

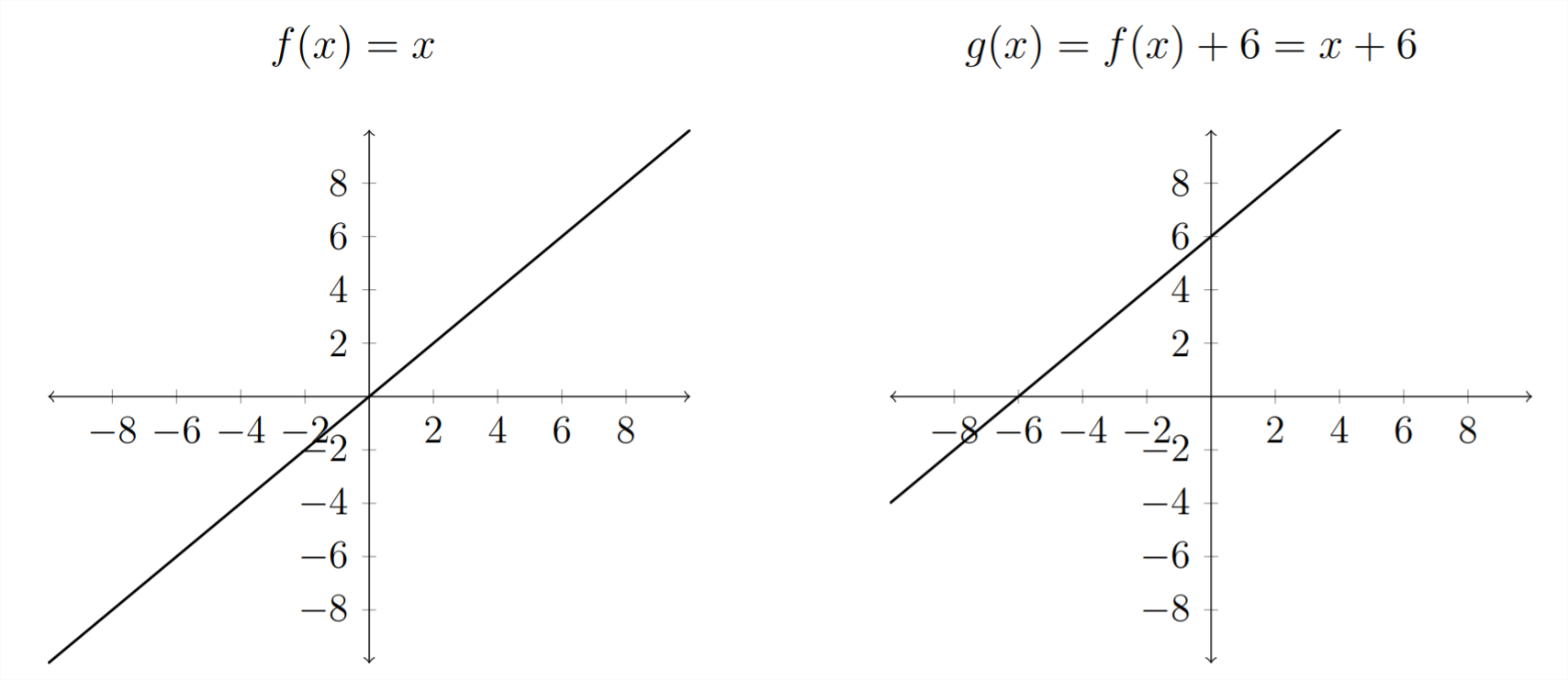
Vertical Shifts
So, if we have a general function \(f(x)\) that is described by a graph, we can determine a graph for \(f(x)+k,\) where \(k\) is some number that will either shift \(f(x)\) up \((\text { if } k>0)\) or down (if \(k<0\) )
For example, consider the following graph for \(f(x)\)

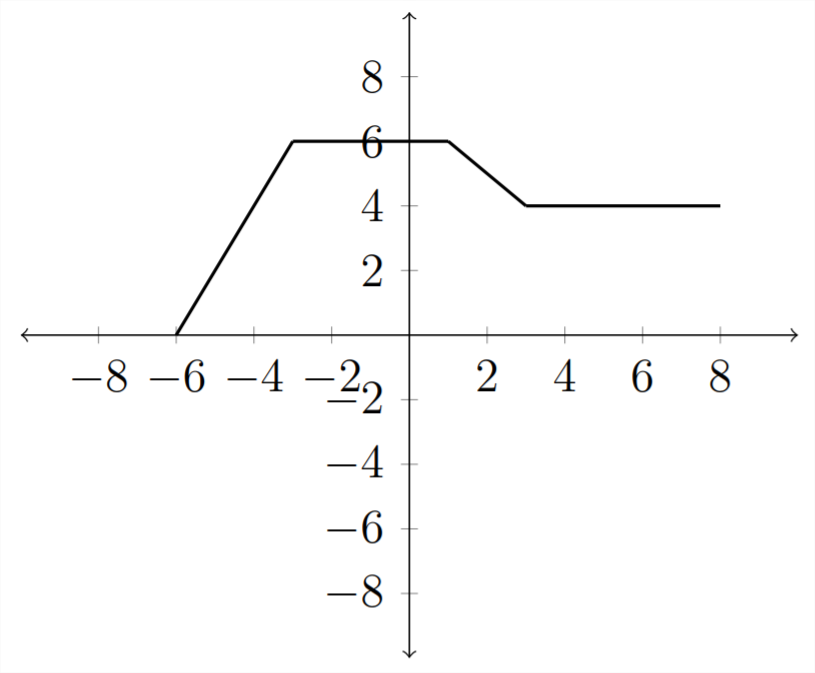
Then, if we want a graph for \(f(x)-2\), just shift all the \(y\) -values down 2 places:

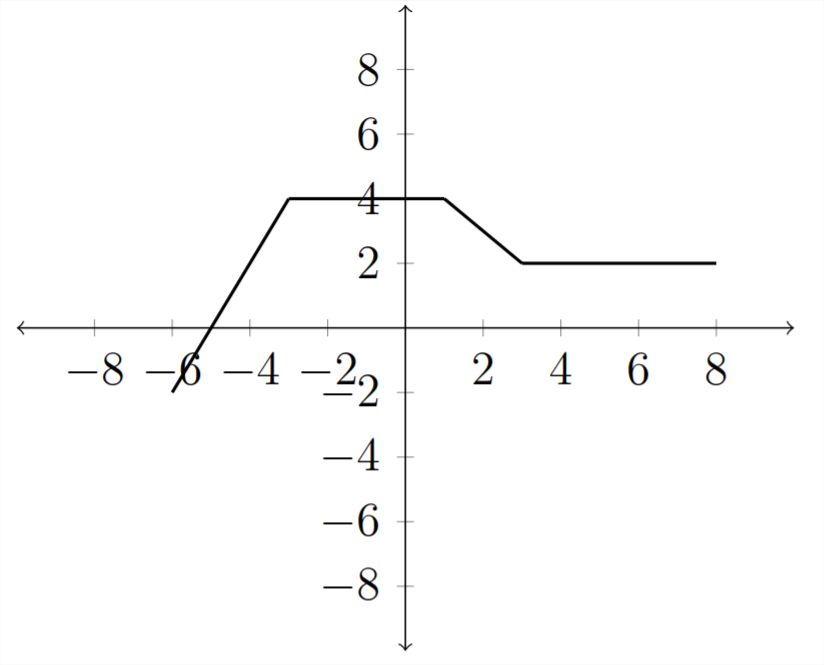
This is a standard vertical shift transformation of a function.

Horizontal Shifts
A function may also be shifted horizontally by adding or subtracting a number inside the parentheses.
If we start with our original function \(f(x)\)

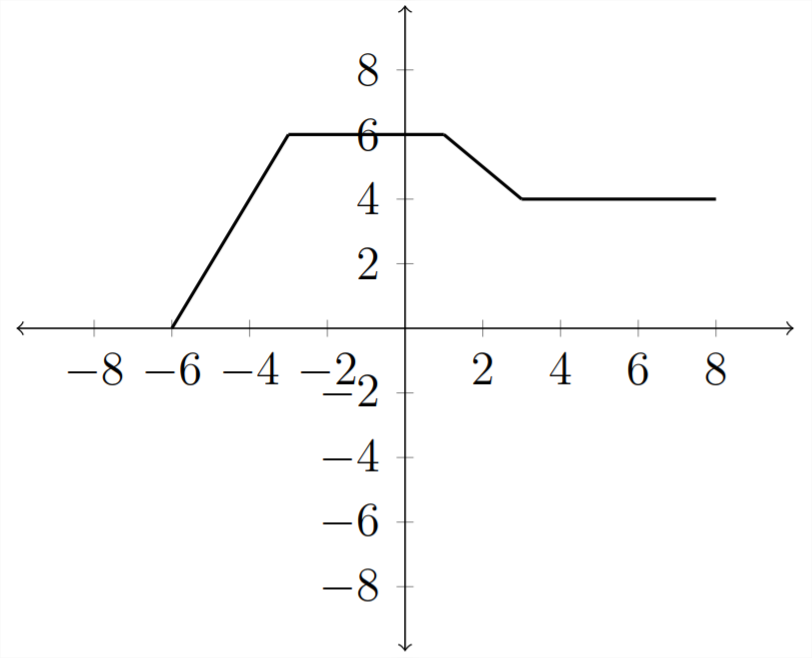
Then the transformation \(f(x-2)\) will shift the graph horizontally, except that it will move in the opposite direction of the sign. The \(f(x-2)\) shift will move the graph 2 places to the right whereas a shift of \(f(x+2)\) will move the graph 2 places to the left.

The reason why this happens will be more clear if we look at a table of values for the function:

Now, if, instead of \(f(x),\) we want \(f(x-2),\) then we add another column to the table:

Notice that to have the same \(y\) -value as the original graph, we must go 2 places to the right so that after we subtract 2 from the \(x\) -value, we arrive back at the original \(x\) -value. So the graph of \(f(x-2)\) will look like this:

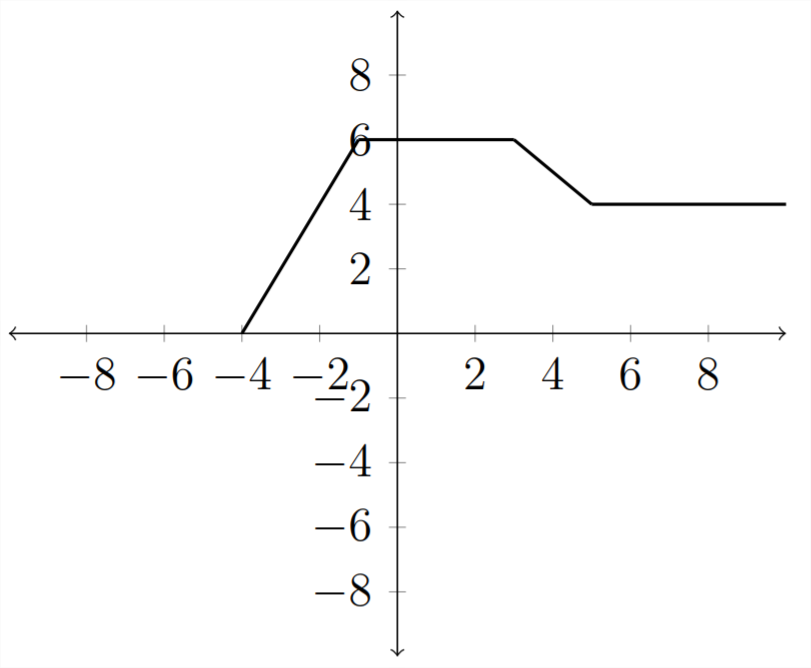
Notice how the values in the graph match up with the values in the table.

Reflections
Negating the \(x\) or \(y\) values of a function will have the effect of reflecting the function over the \(y\) or \(x\) axis. If we consider the function \(f(x)\) - the same one we used in the previous examples:

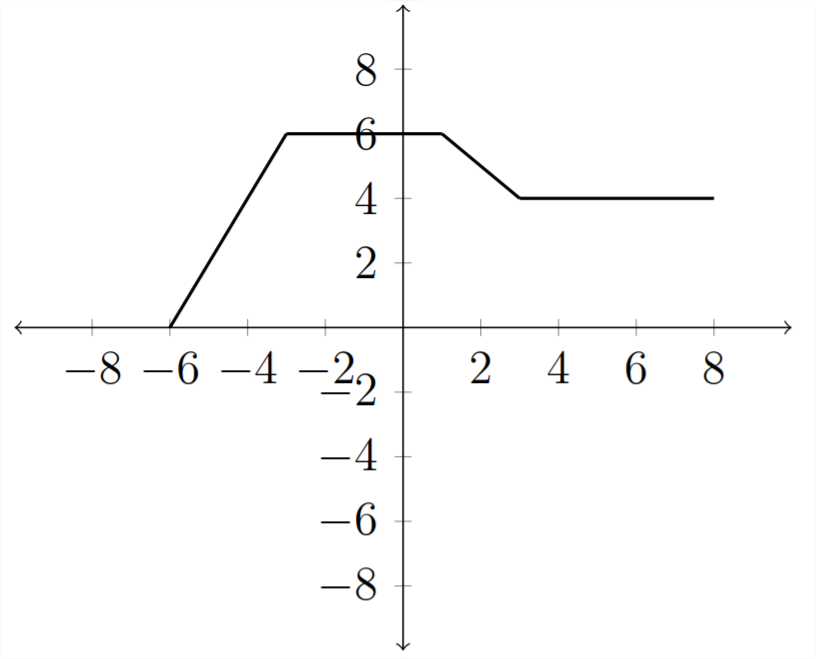
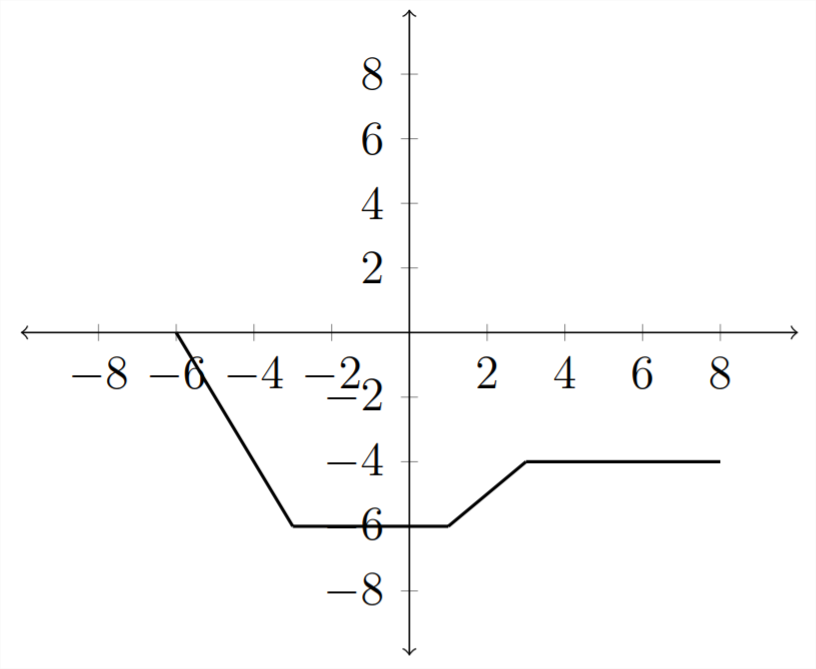
Then the graph of \(y=-f(x)\) will be reflected over the \(x\) -axis. The negative sign in front of the function negates all of the \(y\) values, reflecting them over the \(x\) -axis. Lets look at this in a table of values:

So the graph would look like this:

On the other hand, if we negate the \(x\) -variable \((f(-x)),\) then the function values previously associated with the positive values of \(x\) would be associated with the negative values of \(x\) and vice versa. This would reflect the function over the \(y\) -axis.
If we again consider our original function and a table of values:

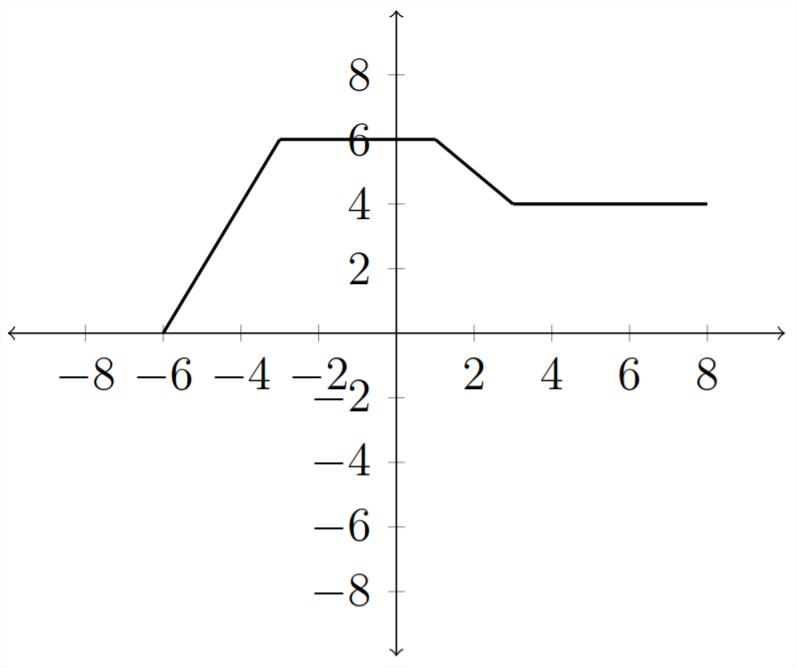
In the table:

And the graph would be reflected over the \(y\) -axis:

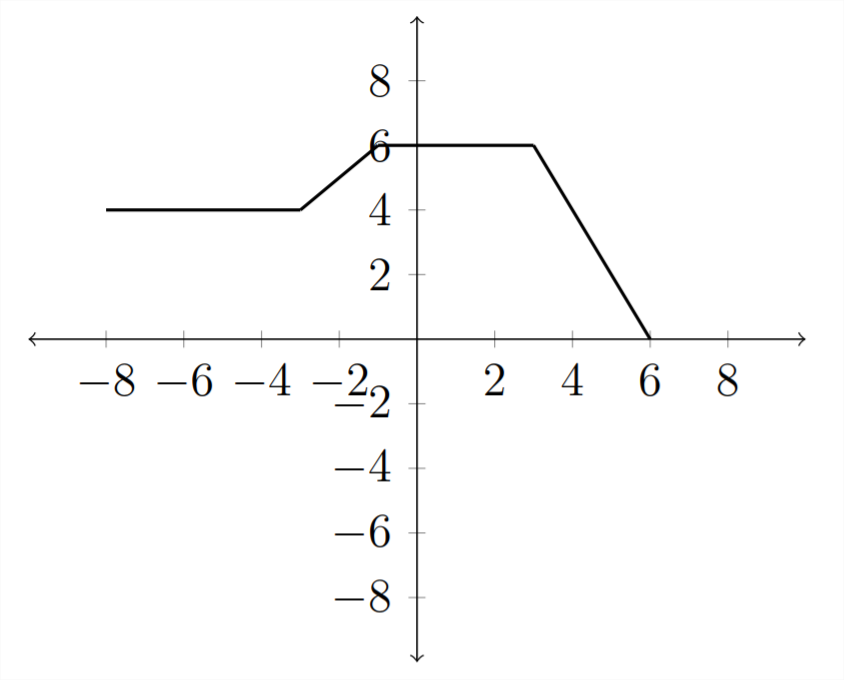
Stretching and compressing graphs

The last type of transformation we will examine is that of stretching or compressing a graph by multiplying inside or outside the parentheses. Starting with our familiar example function \(y=f(x)\)

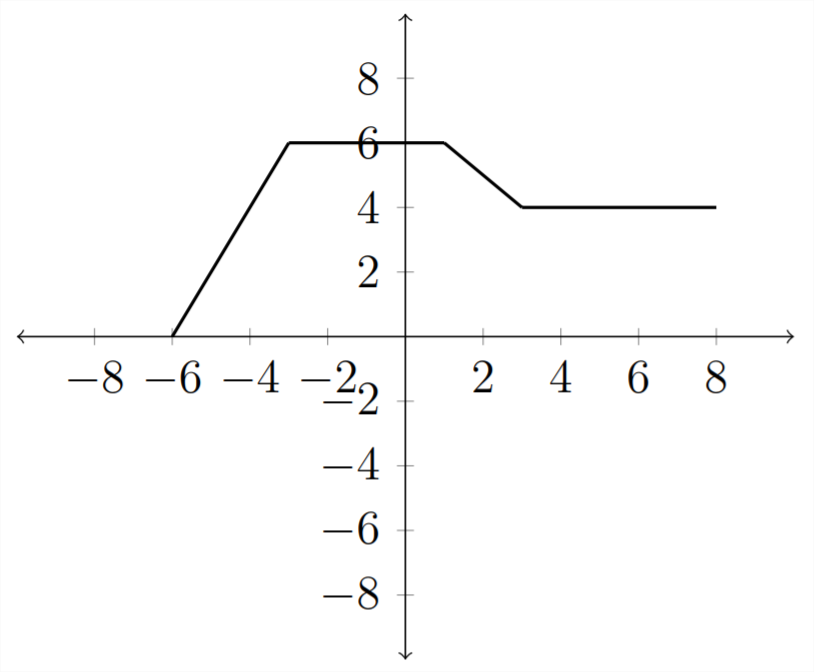
If we multiply the function by a constant outside of the parentheses: \(y=2 f(x)\) then this will have the effect of multiplying all of the \(y\) values by \(2 .\) In the table:


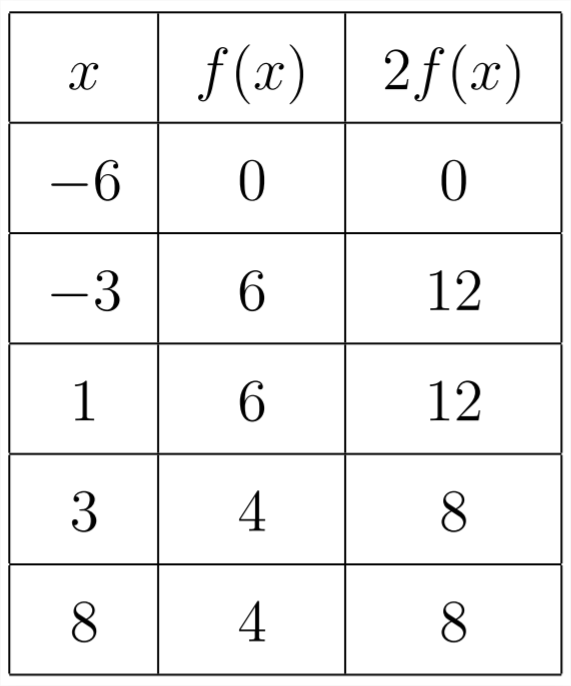
The graph of \(y=2 f(x)\) would look like this:

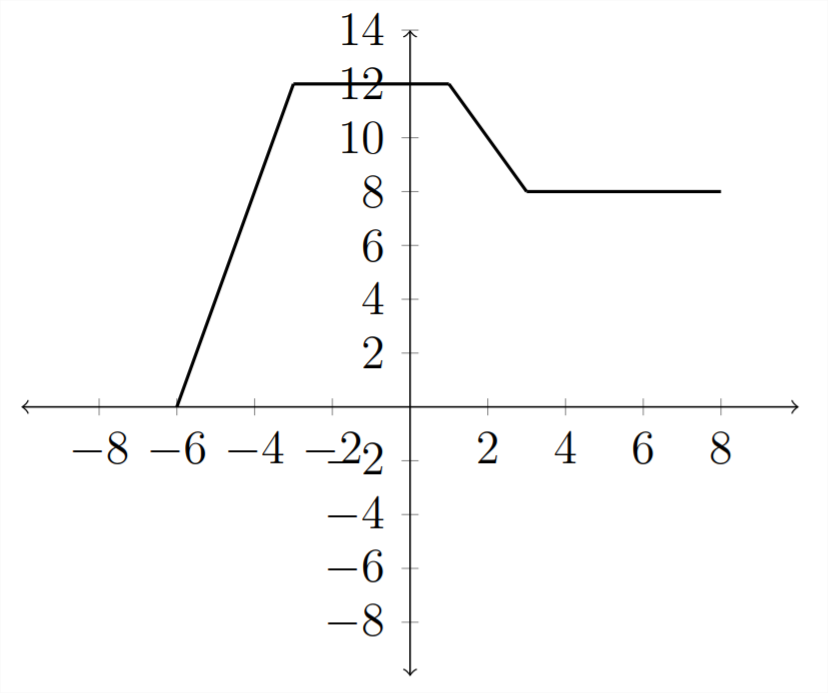
In a similar way, multiplying by a number less than 1 would compress the graph. The graph for \(y=\frac{1}{2} f(x)\) is below:

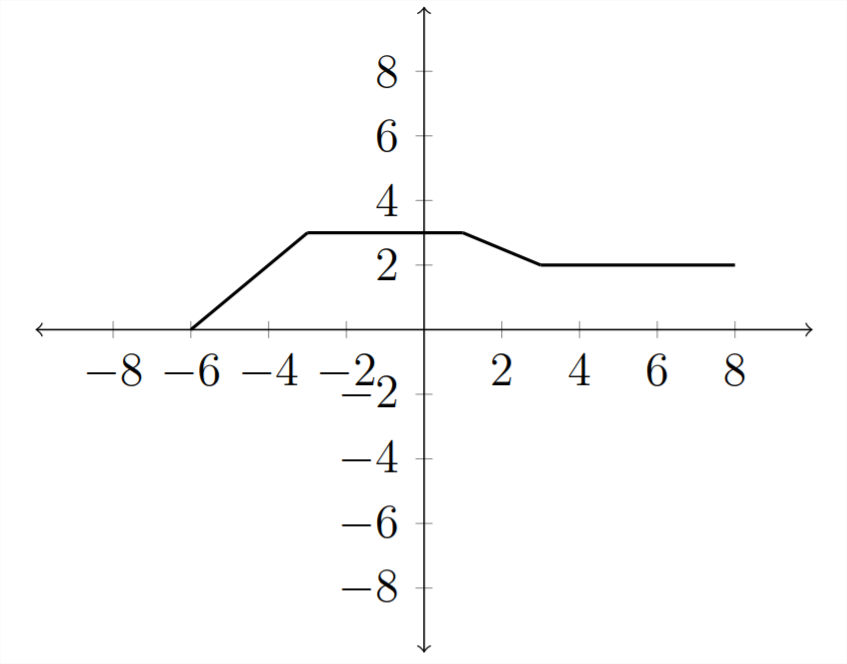
Multiplying inside the parentheses affects the \(x\) variables.
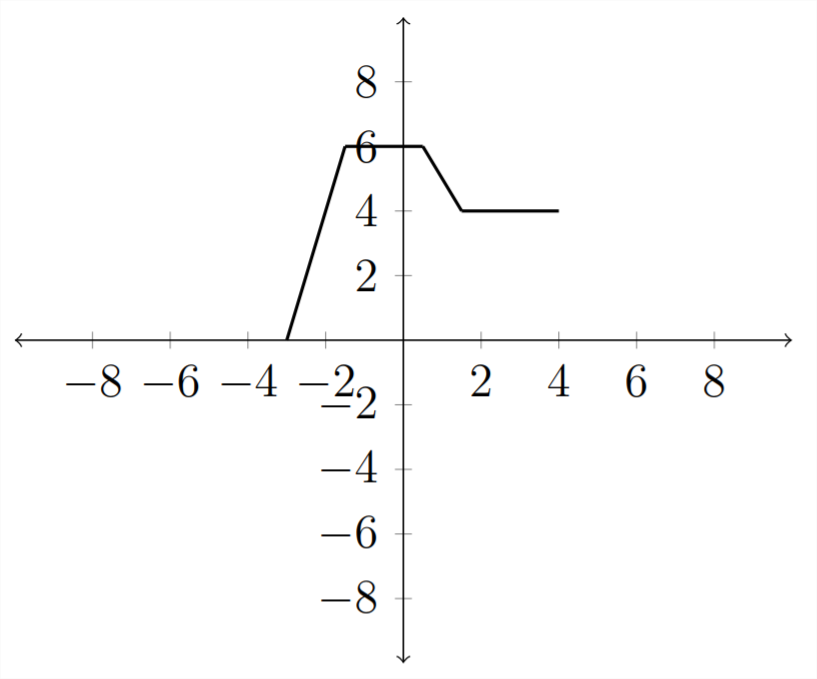
If we consider the function \(y=f(2 x)\), then this will have the effect of compressing the graph along the \(x\) -axis:

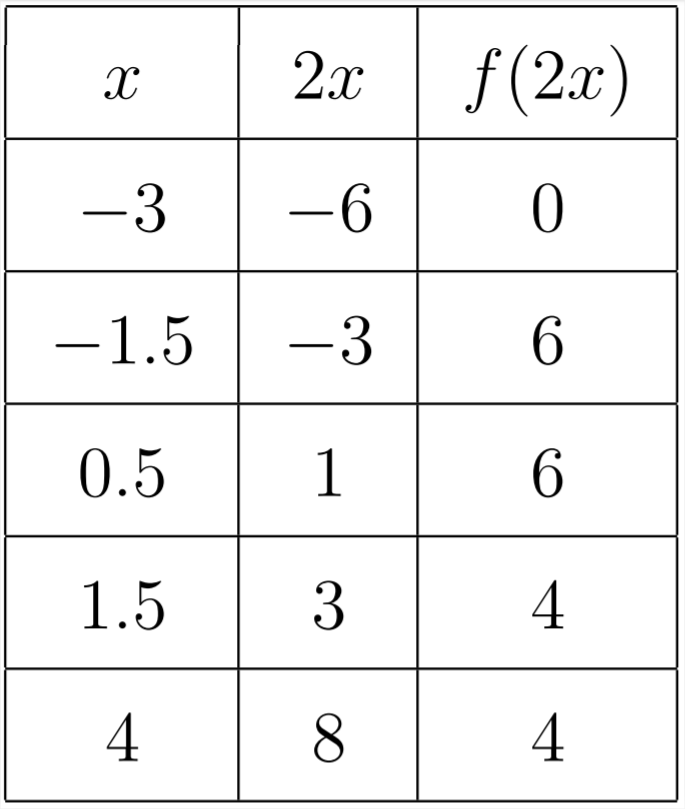
Notice how each \(x\) value had to be cut in half so that when we multiplied it by 2 we ended up with the original \(x\) value. The graph would look like this:

Multiplying inside the parentheses by a number less than one would stretch the graph out.


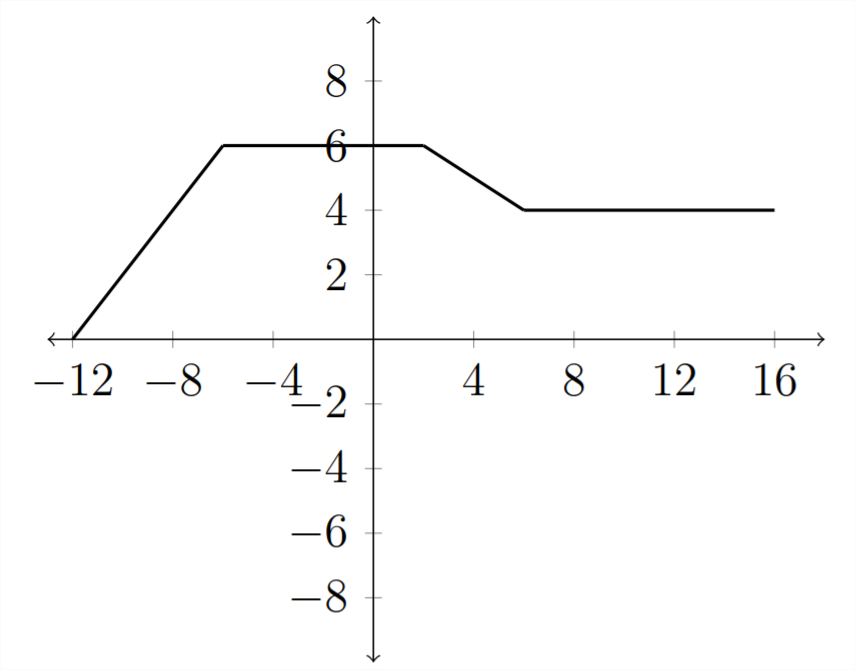
In these examples, we have considered only one transformation at a time. In the exercises you will need to consider the effect of several transformations at once.

Exercises 4.4
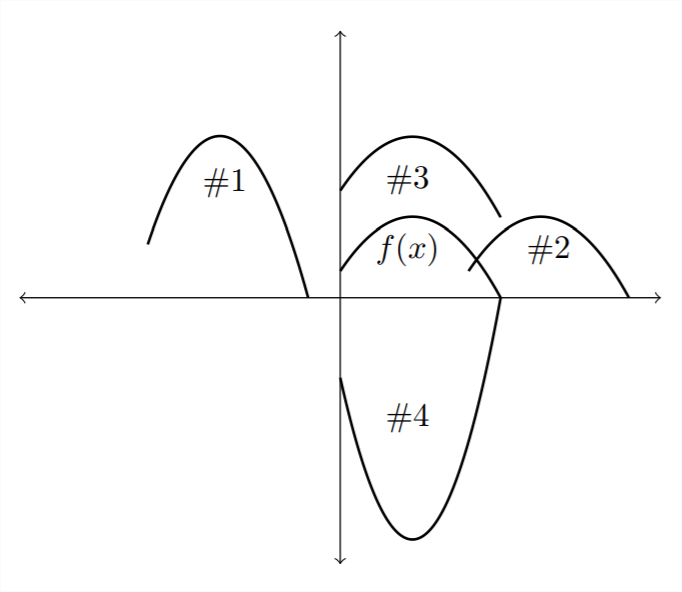
1) Match each of the functions on the graph to the appropriate transformation described below.
a) \(\quad f(x-4)\)
b) \(\quad f(x)+3\)
c) \(\quad -3 f(x)\)
d) \(\quad 2 f(x+6)\)

2) Match each of the descriptions with the appropriate function transformation.

\begin{array}{cc}
a) \quad y=f(x-1) & 1) \text{Shift left one unit} \\
b) \quad y=f(x)-1 & 2) \text{Reflect over \(x\) -axis, then shift left one unit} \\
c) \quad y=f(x)+1 & 3) \text{Shift right one unit} \\
d) \quad y=f(x+1) & 4) \text{Reflect over \(x\) -axis, then shift up one unit} \\
e) \quad y=f(-x)+1 & 5) \text{Reflect over \(x\) -axis, then shift down one unit} \\
f) \quad y=f(-x)-1 & 6) \text{Shift down one unit} \\
g) \quad y=-f(x)+1 & 7) \text{Reflect over \(x\) -axis, reflect over \(y\) -axis, then shift up one unit} \\
h) \quad y=-f(x+1) & 8 \text{Shift left one unit, reflect over \(y\) -axis, then shift up one unit} \\
i) \quad y=-f(x)-1) & 9) \text{Shift up one unit} \\
j) \quad y=f(-x+1) & 10) \text{Reflect over \(y\) -axis, then shift up one unit} \\
k) \quad y=-f(-x) & 11) \text{Reflect over \(y\) -axis, then shift down one unit} \\
\end{array}

3) Match each of the descriptions with the appropriate function transformation.
\begin{array}{cc}
a) \quad y=f(x+2)+3 & 1) \text{Shift left 2 units, then shift down 3 units} \\
b) \quad y=f(x+3)+2 & 2) \text{Shift left 3 units, then shift up 2 units} \\
c) \quad y=f(x-2)+3 & 3) \text{Shift right 3 units, then shift up 2 units} \\
d) \quad y=f(x-2)-3 & 4) \text{Shift left 3 units, then shift down 2 units} \\
e) \quad y=f(x+2)-3 & 5) \text{Shift right 3 units, then shift down 2 units} \\
f) \quad y=f(x-3)+2 & 6) \text{Reflect over the \(y\) -axis, then shift up 2 units} \\
g) \quad y=f(x-3)-2 & 7) \text{Reflect over \(x\) -axis, then shift right 2 units} \\
h) \quad y=f(x+3)-2 & 8) \text{Reflect over \(x\) -axis, then shift left 2 units} \\
i) \quad y=-f(x+2) & 9) \text{Shift left 2 units, then reflect over the \(y\) -axis} \\
j) \quad y=-f(x-2) & 10) \text{Shift right 2 units, then shift up 3 units} \\
k) \quad y=f(2-x) & 11) \text{Shift left 2 units, then shift up 3 units} \\
\ell) \quad y=f(-x)+2 & 12) \text{Shift right 2 units, then shift down 3 units}
\end{array}

Apply the transformations indicated for each function.

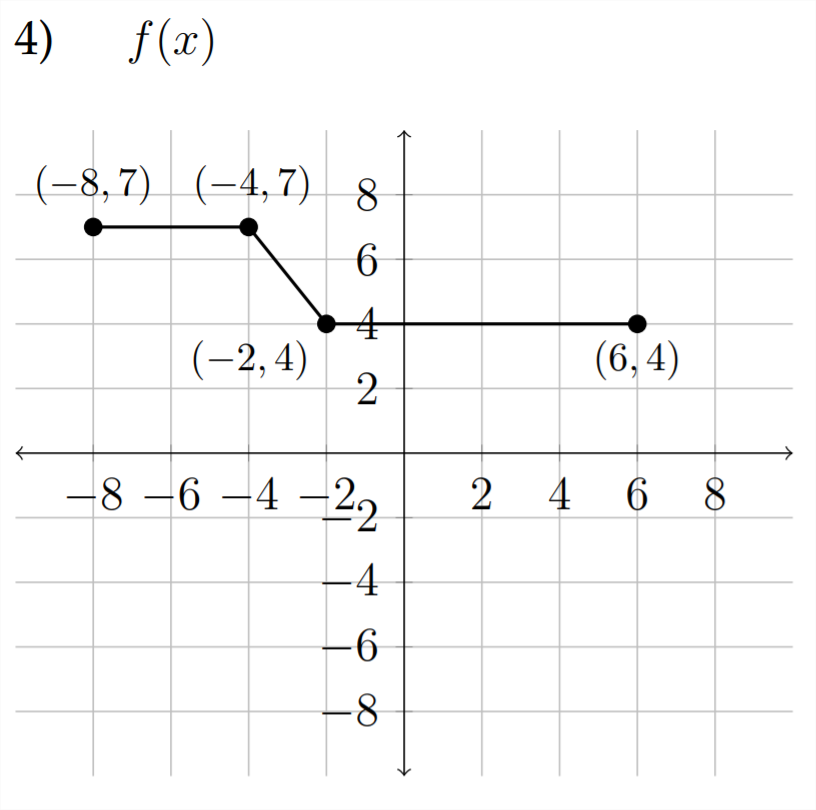
a) \(\quad f(x-3)\)
b) \(\quad-f(x)+2\)
c) \(\quad \frac{1}{2} f(x-1)\)
d) \(\quad f(-x)+1\)

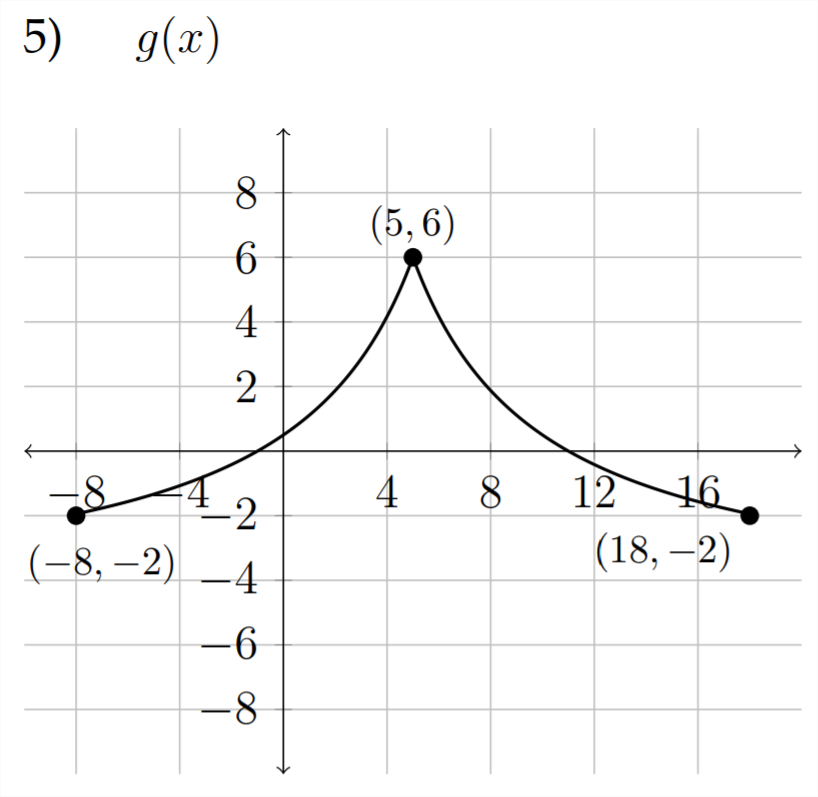
a) \(\quad g(x)-3\)
b) \(\quad-g(x)-1\)
c) \(\quad 2 g(x+2)\)
d) \(\quad g(2 x)-1\)

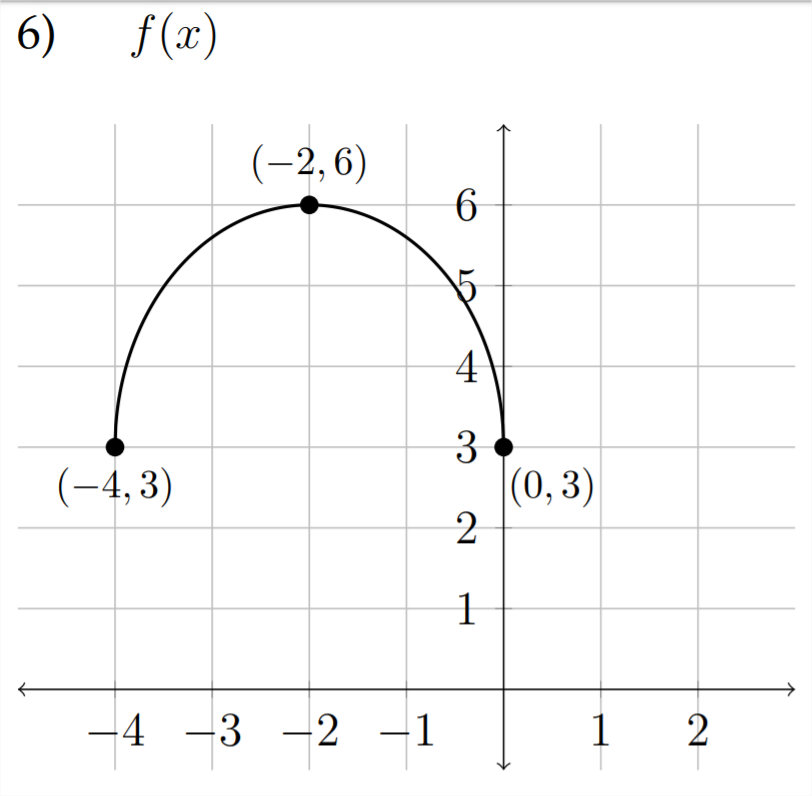
a) \(\quad f(x)+2\)
b) \(\quad-f(x-1)\)
c) \(\quad f(x-1)-3\)
d) \(\quad \frac{1}{3} f(x)+4\)

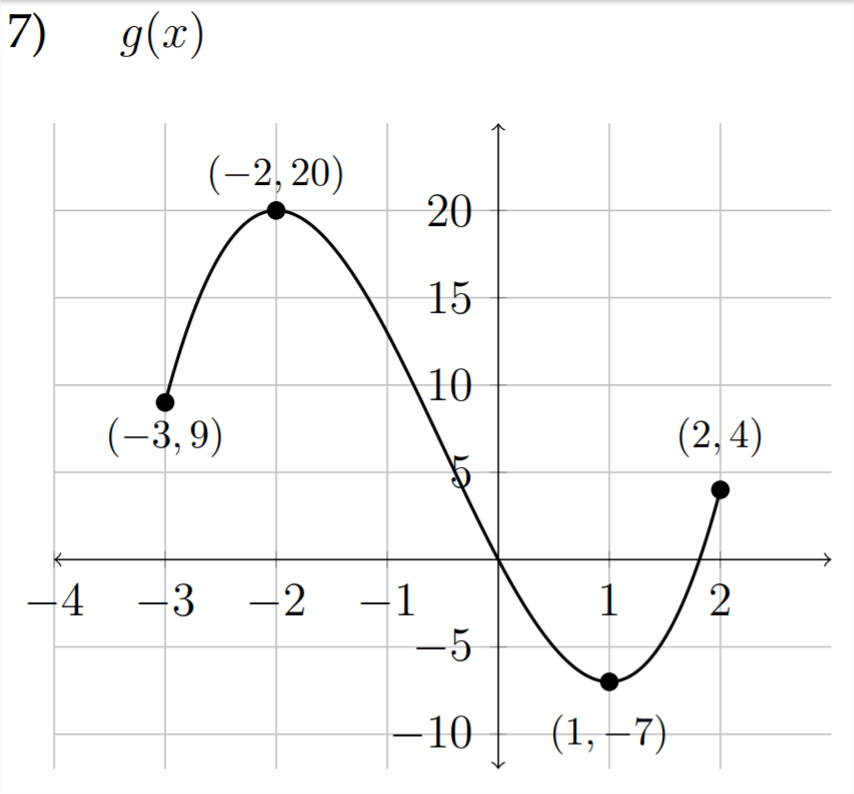
a) \(\quad g(x-2)\)
b) \(\quad-g(x)+1\)
c) \(\quad 2 g(x-1)\)
d) \(\quad \frac{1}{2} g(x)-3\)