9.3: The Vertical Shift of a Trigonometric Function

Last updated
Save as PDF

Page ID: 41325

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

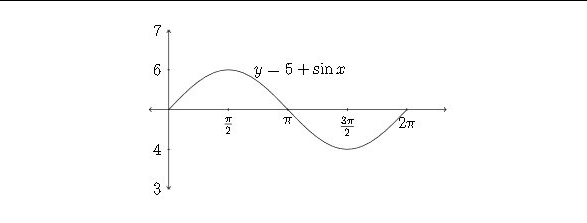
If a constant is added or subtracted to a trigonometric function, this will affect the $y$ -values of the function If we consider the function $y-5+\sin x,$ then each of the standard $y$ -values would have 5 added to if, which would shift the graph up 5 units.
The chart below considers just the quadrantal values for the sine function:
\begin{tabular}{|c|c|c|}
\hline$\theta$ & $\sin \theta$ & $5+\sin \theta$ \\
\hline 0 & 0 & 5 \\
\hline$\pi / 2$ & 1 & 6 \\
\hline$\pi$ & 0 & 5 \\
\hline $3 \pi / 2$ & -1 & 4 \\
\hline $2 \pi$ & 0 & 5 \\
\hline
\end{tabular}

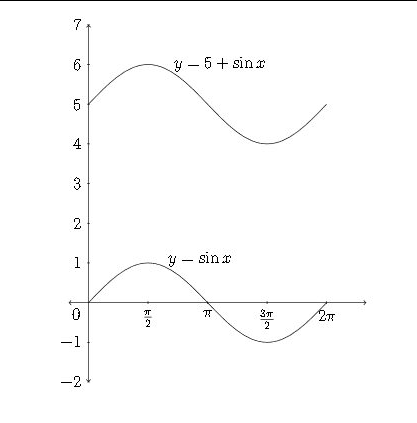
$clipboard_ede5c070d07c8fe55cf1bb0789cfb4041.png$

Sometimes the $x$ -axis is drawn through the line that is the new "zero" or "midline" for the function - in this case it would be $y-5$

$clipboard_e87e20b7638d21dc26d41fc558583cbb8.png$

Likewrise, a negative constant would move the graph down, as each y-value would be less than the corresponding $y$ -value in the standard sine function

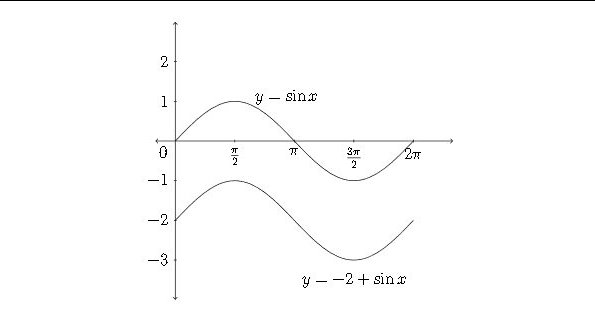
$clipboard_eaa9d8adfd3a3e651563da20ddf802696.png$

In the previous examples the constant has been written in front of the sine function for clarity. Often the constant is written after the function:
\[ \begin{array}{c}
y-\sin x+5 \\
\mathrm{or} \\
y-\sin x-2
\end{array}
\]

We have now examined three of the four transformations of trigonometric functions that are discussed in this chapter - amplitude, period and vertical shift. A general equation for a sinusoid that involves these three transformations would be:
\[ y=A \sin (B x)+D
\] Or
\[ y=A \cos (B x)+D
\] In determining an equation from a graph that involves a vertical shift, the value of $A$ will be half the distance between the maximum and minimum values:
\[ A=\frac{m a x-m i n}{2}
\] and the value of $D$ will be the average of the maximum and minimum values:
\[ D=\frac{m a x+m i n}{2}
\]

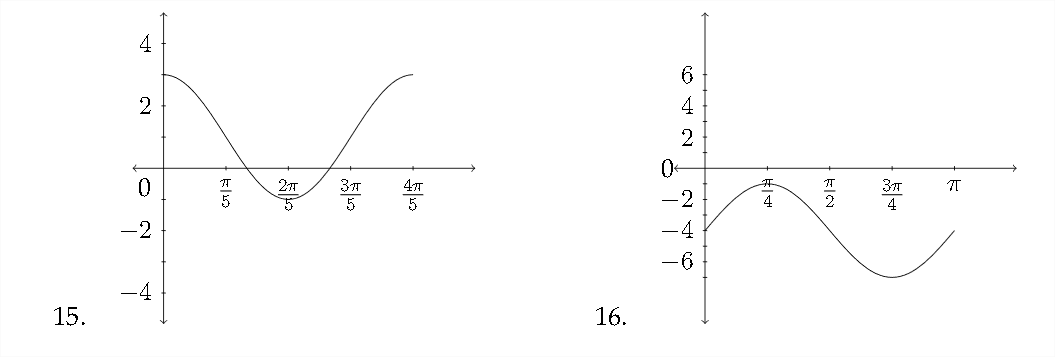
Example
Determine an equation that satisfies the given graph.

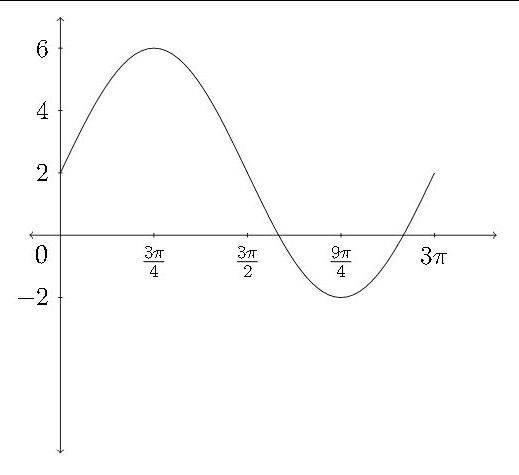
$clipboard_eb9a5a41b697448191e95f61ae0e448b2.png$

In this graph, the maximum $y$ -value is 6 and the minimum $y$ -value is $-2 .$ The average of these two:
\[ \frac{m a x+m i n}{2}=\frac{6+(-2)}{2}=\frac{4}{2}=2=D
\] is the value of $D,$ the vertical shift.
The distance between 6 and -2 is $6-(-2)=8 .$ Half the distance between the $\max$ and $\min$ is $4,$ which is the value of $A$
\[ \frac{m a x-m i n}{2}=\frac{6-(-2)}{2}=\frac{8}{2}=4=A
\]

The graph completes one full cycle between 0 and $3 \pi,$ so the period would be $3 \pi$ and the value of $B$ would be $B=\frac{2 \pi}{P}=\frac{2 \pi}{3 \pi}=\frac{2}{3}=B .$ So a correct equation for the graph would be:
\[ y=4 \sin \frac{2}{3} x+2
\]

Exercises 2.3
Determine the Amplitude, Period and Vertical Shift for each function below and graph one period of the function. Identify the important points on the $x$ and $y$ axes.
1. $\quad y=\sin x+1$
2. $\quad y=\cos x-1$
3. $\quad y=2 \cos x-\frac{1}{2}$
4. $\quad y=5 \sin x+4$
5. $\quad y=-\sin \left(\frac{1}{4} x\right)+1$
6. $\quad y=-\cos (2 x)+7$
7. $\quad y=\frac{1}{3} \sin (\pi x)-4$
8. $\quad y=-\frac{1}{2} \cos (2 \pi x)+2$
9. $\quad y=5 \cos \left(\frac{1}{2} x\right)+1$
$10 . \quad y=4 \sin \left(\frac{1}{3} x\right)-1$
11. $\quad y=3 \cos x+2$
12. $\quad y=2 \sin x+3$
13. $\quad y=2-4 \cos (3 x)$
14. $\quad y=5-3 \sin (2 x)$

Determine an equation that satisfies the given graph.

$clipboard_ef06827032e823eb3136b6c1ebd4b1738.png$

$clipboard_e43a8453a2e534595bf2ec5bd31d3044e.png$