2.2: Solving Equations - Multiple Steps
- Page ID
- 19857
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall the “Wrap” and “Unwrap” discussion from Section 2.1. To wrap a present we put the gift paper on, put the tape on, and put the decorative bow on. To unwrap the gift, we must “undo” each of these steps in inverse order. Hence, to unwrap the gift we take off the decorative bow, take off the tape, and take off the gift paper.
Now, imagine a machine that multiplies its input by \(3\), then adds \(5\) to the result. This machine is pictured on the left in Figure \(\PageIndex{1}\).
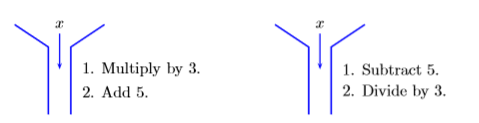
Figure \(\PageIndex{1}\): The second machine “unwraps” the first machine.
To “unwrap” the effect of the machine on the left, we need a machine that will “undo” each of the steps of the first machine, but in inverse order. The “unwrapping” machine is pictured on the right in Figure \(\PageIndex{1}\). It will first subtract \(5\) from its input, then divide the result by \(3\). Note that each of these operations “undoes” the corresponding operation of the first machine, but in inverse order.
The following argument shows that the second machine “undoes” the operation of the first machine.
- Drop the integer \(4\) into the machine on the left in Figure \(\PageIndex{1}\). This machine will first multiply \(4\) by \(3\), then add \(5\) to the result. The result is \(3(4) + 5\), or \(17\).
- To “unwrap” this result, drop \(17\) into the machine on the right. This machine first subtracts \(5\), then divides the result by \(3\). The result is \((17-5)/3\), or \(4\), the original integer that was put into the first machine.
Example \(\PageIndex{1}\)
Solve for \(x : 3 x+5=14\).
Solution
On the left, order of operations demands that we first multiply \(x\) by \(3\), then add \(5\). To solve this equation for \(x\), we must “undo” each of these operations in inverse order. Thus, we will first subtract \(5\) from both sides of the equation, then divide both sides by \(3\).
\[\begin{aligned} 3x+5 &=14 \quad \color{Red} \text{ Original equation. } \\ 3x+5-5 &=14-5 \quad \color{Red} \text{ To "undo" adding 5, subtract 5 from both sides of the equation. } \\ 3x &=9 \quad \color{Red} \text{ Simplify both sides. } \\ \dfrac{3 x}{3} &=\dfrac{9}{3} \quad \color{Red} \text{ To "undo" multiplying by 3, divide both sides of the equation by 3. } \\ x&=3 \quad \color{Red} \text{ Simplify both sides. } \end{aligned} \nonumber \]
Check: To check the solution, substitute \(3\) for \(x\) in the original equation and simplify.
\[\begin{aligned} 3x+5 &=14 \quad \color{Red} \text{ Original equation. } \\ 3(3)+5 &=14 \quad \color{Red} \text{ Substitute 3 for x. } \\ 9+5 &=14 \quad \color{Red} \text{Multiply first: 3(3) = 9. } \\ 14 &=14 \quad \color{Red} \text{ Add: 9 + 5 = 14. } \end{aligned} \nonumber \]
Because the last line of the check is a true statement, this guarantees that \(3\) is a solution of the original equation.
Exercise \(\PageIndex{1}\)
Solve for \(x :2 x+3=7\).
- Answer
-
\(x=2\)
Let’s try an equation with fractions.
Example \(\PageIndex{2}\)
Solve for \(x : \dfrac{x}{5}-\dfrac{2}{3}=\dfrac{1}{2}\).
Solution
On the left, order of operations demands that we first divide \(x\) by \(5\), then subtract \(2/3\). To solve this equation for \(x\), we must “undo” each of these operations in inverse order. Thus, we will first add \(2/3\) to both sides of the equation, then multiply both sides of the resulting equation by \(5\).
\[\begin{aligned} \dfrac{x}{5}-\dfrac{2}{3} &=\dfrac{1}{2} \quad \color{Red} \text{ Original equation. }\\ \dfrac{x}{5}-\dfrac{2}{3}+\dfrac{2}{3} &=\dfrac{1}{2}+\dfrac{2}{3} \quad \color{Red} \text{ To "undo" subtracting 2/3, add 2/3 to both sides of the equation. } \end{aligned} \nonumber \]
On the left, we simplify. On the right, we make equivalent fractions with a common denominator.
\[\begin{aligned} \dfrac{x}{5}&=\dfrac{3}{6}+\dfrac{4}{6} \quad \color{Red} \text { Make equivalent fractions } \\ \dfrac{x}{5}&=\dfrac{7}{6} \quad \color{Red} \text { Add: } \dfrac{3}{6}+\dfrac{4}{6}=\dfrac{7}{6} \end{aligned} \nonumber \]
Now we “undo” dividing by five by multiplying both sides of the equation by \(5\).
\[\begin{aligned} \left(\dfrac{x}{5}\right)&=5\left(\dfrac{7}{6}\right) \quad \color{Red} \text { Multiply both sides by } 5 \\ x&=\dfrac{35}{6} \quad \color{Red} \text { On the left, simplify. On the right, multiply: } 5\left(\dfrac{7}{6}\right)=\dfrac{35}{6} \end{aligned} \nonumber \]
Check: Let’s use the TI-84 to check this solution.
- Store the value \(35/6\) in the variable \(X\) using the following keystrokes.

The result is shown in Figure \(\PageIndex{2}\).
- Enter the left-hand side of the original equation: \(x/5 - 2/3\). Use the following keystrokes.

The result is shown in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Checking the solution to x/5−2/3=1/2.
- Press the MATH button on your calculator (see Figure \(\PageIndex{3}\)), then select 1:►Frac, then press the ENTER button. This will convert the decimal result to a fraction (see Figure \(\PageIndex{3}\)).
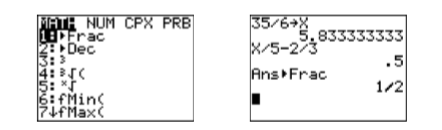
Figure \(\PageIndex{3}\): Changing the result to a fraction.
Note that the result is \(\dfrac{1}{2},\) showing that \(\dfrac{35}{6}\) is a solution of \(\dfrac{x}{5}-\dfrac{2}{3}=\dfrac{1}{2}\).
Exercise \(\PageIndex{2}\)
Solve for \(x: \dfrac{x}{2}-\dfrac{3}{5}=\dfrac{1}{4}\).
- Answer
-
\(x = 17/10\)
Let’s try an equation with decimals.
Example \(\PageIndex{3}\)
Solve for \(x : 5.2 x+2.3=-3.94\).
Solution
On the left, order of operations demands that we first multiply \(x\) by \(5.2\), then add 2.3. To solve this equation for \(x\), we must “undo” each of these operations in inverse order. Thus, we will first subtract \(2.3\) from both sides of the equation, then divide both sides by \(5.2\).
\[\begin{aligned} 5.2 x+2.3 &=-3.94 \quad \color{Red} \text{ Original equation. }\\ 5.2 x+2.3-2.3 &=-3.94-2.3 \quad \color{Red} \text{ To "undo" adding 2.3, subtract 2.3 from both sides.}\\ 5.2 x &=-6.24 \quad \color{Red} \text{ On the left, simplify. On the right, add: -3.94-2.3=-6.24. }\\ \frac{5.2 x}{5.2} &=\frac{-6.24}{5.2} \quad \color{Red} \text{ To undo multiplying by 5.2, divide both sides by 5.2. }\\ x &=-1.2 \quad \color{Red} \text{ On the left, simplify. On the right, divide: -6.24/5.2=-1.2. } \end{aligned} \nonumber \]
Check: To check the solution, substitute \(-1.2\) for \(x\) in the original equation and simplify.
\[\begin{aligned} 5.2 x+2.3 &=-3.94 \quad \color{Red} \text{ Original equation. }\\ 5.2(-1.2)+2.3 &=-3.94 \quad \color{Red} \text{ Substitute -1.2 for x. }\\ -6.24+2.3 &=-3.94 \quad \color{Red} \text{ Multiply: 5.2(-1.2)=-6.24 }\\ -3.94 &=-3.94 \quad \color{Red} \text{ Add: -6.24+2.3=-3.94 } \end{aligned} \nonumber \]
Because the last line of the check is a true statement, this guarantees that \(-1.2\) is a solution of the original equation.
Exercise \(\PageIndex{3}\)
Solve for \(x: 3.25-1.2 x=0.37\).
- Answer
-
\(x=2.4\)
Variables on Both Sides of the Equation
It is not uncommon that the variable you are solving for appears in terms on both sides of the equation. Consider, for example, the equation \(2x+3=5−7x\). In cases like this, it is helpful to have a general understanding of what it means to “solve for \(x\).”
Solve for x
When asked to solve an equation for \(x\), the goal is to manipulate the equation into the final form
\(x=\text{"Stuff"}\)
where “Stuff” is a valid mathematical expression that may contain other variables, mathematical symbols, etc., but it must not contain any occurrence of the variable \(x\).
In this section, “Stuff” will always be a single number, but in Section 2.4, Formulae, “Stuff” will take on added complexity, including variables other than \(x\).
Strategy for solving for \(x\)
When asked to solve an equation for \(x\), a common strategy is to isolate all terms containing the variable \(x\) on one side of the equation and move all terms not containing the variable \(x\) to the other side of the equation.
Example \(\PageIndex{4}\)
Solve \(3-2 x=5 x+9\) for \(x\).
Solution
We need to isolate all terms containing \(x\) on one side of the equation. We can eliminate \(5x\) from the right-hand side of \(3−2x =5x+9\) by subtracting \(5x\) from both sides of the equation.
\[\begin{aligned} 3-2x &=5x+9 \quad \color{Red} \text { Original equation. } \\ 3-2x-5x & =5x+9-5x \quad \color{Red} \text { Subtract } 5x \text { from both sides. } \\ 3-7x &=9 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Next, eliminate \(3\) from the left-hand side of the last equation by subtracting \(3\) from both sides of the equation.
\[\begin{aligned} 3-7x-3 & =9-3 \quad \color{Red} \text { Subtract } 3 \text { from both sides. } \\ -7x & =6 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Note how we have isolated all terms containing \(x\) on one side of the equation.
\[\begin{aligned} \dfrac{-7 x}{-7}&=\dfrac{6}{-7} \quad \color{Red} \text { Divide both sides by }-7 \\ x&=-\dfrac{6}{7} \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Check: To check the solution, substitute \(-6/7\) for \(x\) in the original equation.
\[\begin{aligned}
3-2 x &=5 x+9 \quad \color{Red} \text { Original equation. }\\
3-2\left(-\dfrac{6}{7}\right) &=5\left(-\dfrac{6}{7}\right)+9 \quad \color{Red} \text { Substitute -6/7 for x. }\\
3+\dfrac{12}{7} &=-\dfrac{30}{7}+9 \quad \color{Red} \text { Multiply: } -2(-6/7)=12/7 \text { and } 5(-6/7)=-30/7. \\
\dfrac{21}{7}+\dfrac{12}{7} &=-\dfrac{30}{7}+\dfrac{63}{7} \quad \color{Red} \text { Make equivalent fractions with a common denominator. }\\
\dfrac{33}{7} &=\dfrac{33}{7} \quad \color{Red} \text { Add. }
\end{aligned} \nonumber \]
Because the last line of the check is a true statement, this guarantees that \(-6/7\) is a solution of the original equation.
Exercise \(\PageIndex{4}\)
Solve for \(x: 4x+7=5-8x\).
- Answer
-
\(x=-1 / 6\)
Simplifying Expressions when Solving Equations
Sometimes we need to simplify expressions before we can isolate terms containing \(x\).
Example \(\PageIndex{5}\)
Solve for \(x: 2(3 x+1)-3(4-2 x)=-34\).
Solution
We’ll first simplify the expression on the left-hand side of the equation using the Rules Guiding Order of Operations.
\[\begin{aligned}2(3 x+1)-3(4-2 x)&=-34 \quad \color{Red} \text { Original equation. } \\ 6x+2-12+6x&=-34 \quad \color{Red} \text { Multiply: } 2(3 x+1)=6 x+2 \text {, Multiply: } -3(4-2 x)=-12+6 x\\ 12 x-10&=-34 \quad \color{Red} \text { Add: } 6x+6 x=12x \text {, Add: } 2-12=-10\\ \end{aligned} \nonumber \]
To “undo” subtracting \(10\), we add \(10\) to both sides of the equation.
\[\begin{aligned} 12x-10+10&=-34+10 \quad \color{Red} \text { Add } 10 \text { to both sides. } \\ 12x&=-24 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
To “undo” multiplying by \(12\), we divide both sides by \(12\).
\[\begin{aligned} \dfrac{12 x}{12}&=\dfrac{-24}{12} \quad \color{Red} \text { Divide both sides by } 12\\ x&=-2 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Check: Let’s use the TI-84 to check this solution.
- First, store −2 in the variableX using the following keystrokes.
The result is shown in the first image in Figure \(\PageIndex{4}\).
- Enter the left-hand side of original equation: \(2(3x + 1)-3(4-2x)\). Use the following keystrokes.
The result is shown in the second image in Figure \(\PageIndex{4}\).
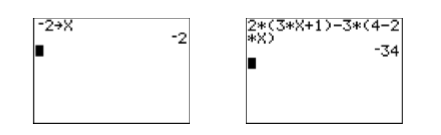
Figure \(\PageIndex{4}\): Checking the solution to \(2(3x + 1)-3(4-2x)=-34\).
Note that when \(-2\) is substituted for \(x\) in the left-hand of the equation, the result is \(-34\), equalling the right-hand side of the equation. Thus, the solution \(-2\) checks.
Exercise \(\PageIndex{5}\)
Solve for \(x : 2 x-(x-2)=2(x+7)\).
- Answer
-
\(x=-12\)
Example \(\PageIndex{6}\)
Solve for \(x : 2 x-5(3-2 x)=4(x-1)\).
Solution
We’ll first simplify the expressions on each side of the equation using the Rules Guiding Order of Operations.
\[\begin{aligned} 2x-5(3-2x)&=4(x-1) \quad \color{Red} \text { Original equation. } \\ 2x-15+10x&=4x-4 \quad \color{Red} \text { On the left, distribute the -5. On the right, distribute the 4.} \\ 12x-15&=4x-4 \quad \color{Red} \text { On the left, add: } 2x+10x=12 x \end{aligned} \nonumber \]
Next, we need to isolate terms containing the variable \(x\) on one side of the equation. To remove the term \(4x\) from the right-hand side, we subtract \(4x\) from both sides of the equation.
\[\begin{aligned} 12x-15-4x&=4x-4-4x \quad \color{Red} \text { Subtract } 4 x \text { from both sides. } \\ 8x-15&=-4 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
To remove the term \(-15\) from the left-hand side, we add \(15\) to both sides of the equation.
\[\begin{aligned} 8x-15+15&=-4+15 \quad \color{Red} \text { Add } 15 \text { to both sides. } \\ 8x&=11 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Finally, to “undo” multiplying by \(8\), we divide both sides by \(8\).
\[\begin{aligned} \dfrac{8x}{8}&=\dfrac{11}{8} \quad \color{Red} \text { Divide both sides by } 8 \\ x&=\dfrac{11}{8} \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Check: Let’s use the TI-84 to check this solution.
- First, store 11/8 in the variable X using the following keystrokes.

The result is shown in the first image in Figure \(\PageIndex{5}\).
- Enter the left-hand side of the original equation: \(2x-5(3-2x)\). Use the following keystrokes.
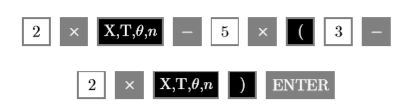
The result is shown in the second image in Figure \(\PageIndex{5}\).
- Enter the right-hand side of the original equation: \(4(x - 1)\). Use the following keystrokes.
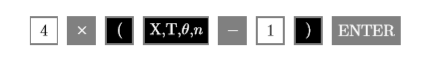
The result is shown in the third image in Figure \(\PageIndex{5}\).
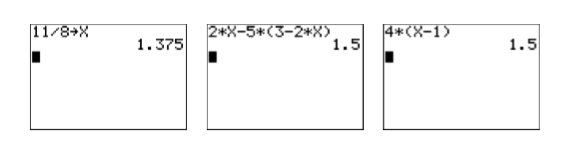
Figure \(\PageIndex{5}\): Checking the solution to \(2x-5(3-2x) = 4(x-1)\).
There is no need to use the 1:►Frac from the MATH menu this time. The fact that both sides of the equation evaluate to an identical \(1.5\) when \(x = 11 /8\) guarantees that \(11/8\) is a solution of \(2x-5(3-2x) = 4(x-1)\).
Exercise \(\PageIndex{6}\)
Solve for \(x:5(1-x)=2(x+3)-(x-1)\).
- Answer
-
\(x=-1 / 3\)
Contributors
David Arnold (Retired Professor (Mathematics) at College of the Redwoods)


