2.4: Formulae

The formulae of science usually contain variable letters other than the variable “Formulae” is the plural for “formula.”x . Indeed, formulae in science typically use several letters. For example, Isaac Newton’s Universal Law of Gravitation says that the magnitude of the force of attraction between two celestial bodies is given by the formula:

\[F=\frac{G M m}{r^{2}} \nonumber \]

where \(m\) usually denotes the mass of the smaller body, \(M\) the mass of the larger body, and \(r\) is the distance between the two bodies. The letter \(G\) represents the universal gravitational constant, having value \(6.67428×10^{-11}\) \(N(m/kg)^2\).

Variable case

Note the use of upper and lower case letter M’s in Newton’s Law of Gravitation. When working with scientific formulae, you must maintain the case of the given letters. You are not allowed to substitute lower for upper case, or upper for lower case in your work.

In Section 2.2, we described the goal that must be met when we are asked to “solve an equation for " \(x\).

Solve for \(x\)

When asked to solve an equation for \(x\), the goal is to manipulate the equation into the final form

\[x=\text {“Stuff”} \nonumber \]
where “Stuff” is a valid mathematical expression that may contain other variables, mathematical symbols, etc., but it must not contain any occurrence of the variable \(x\).

Thus, to solve an equation for \(x\), we need to isolate the terms containing \(x\) on one side of the equation, and all remaining terms on the other side of the equation.

Example \(\PageIndex{1}\)

Solve for \(x : x+a=b\).

Solution

To undo the effects of adding a, subtract a from both sides of the equation.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-a &= b-a \quad \color{Red} \text { Subtract } a \text { from both sides. } \\ x &= b-a \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Exercise \(\PageIndex{1}\)

Solve for \(x : x-c=d\).

Answer

\(x=c+d\)

In Example \(\PageIndex{1}\), note that the answer \(x = b−a\) has the required form, \(x = \text {“Stuff”}\), where “Stuff” is a valid mathematical expression that contains other variables, mathematical symbols, etc., but it does not contain any occurrence of the variable \(x\). Now, what if we were asked to solve the same equation for \(a\), instead of \(x\)?

Example \(\PageIndex{2}\)

Solve for \(a : x+a=b\).

Solution

We are instructed to solve the equation \(x+a = b\) for \(a\). This means that our final answer must have the form \(a = \text {“Stuff”}\), where “Stuff” is a valid mathematical expression that contains other variables, mathematical symbols, etc., but it does not contain any occurrence of the variable \(a\). This means that we must isolate all terms containing the variable \(a\) on one side of the equation, and all remaining terms on the other side of the equation. Now, to undo the effect of adding \(x\), subtract \(x\) from both sides of the equation.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-x &= b-x \quad \color{Red} \text { Subtract } x \text { from both sides. } \\ a &= b-x \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Note that we have \(a = \text {“Stuff”}\), where “Stuff” contains no occurrence of \(a\), the variable we are solving for.

Exercise \(\PageIndex{2}\)

Solve for \(x : x-c=d\).

Answer

\(c=x-d\)

Example \(\PageIndex{3}\)

The formula \(F = kx\), known as “Hooke’s Law”, predicts the force \(F\) required to stretch a spring \(x\) units. Solve the equation for \(k\).

Solution

We are instructed to solve the equation \(F = kx\) for \(k\). This means that our final answer must have the form \(k = \text {“Stuff”}\), where “Stuff” is a valid mathematical expression that may contain other variables, mathematical symbols, etc., but it may not contain any occurrence of the variable \(k\). This means that we must isolate all terms containing the variable \(k\) on one side of the equation, and all remaining terms on the other side of the equation. However, note that all terms containing the variable \(k\) are already isolated on one side of the equation. Terms not containing the variable \(k\) are isolated on the other side of the equation. Now, to “undo” the effect of multiplying by \(x\), divide both sides of the equation by \(x\).

\[\begin{aligned} F&= kx \quad \color{Red} \text { Original equation. } \\ \dfrac{F}{x}&= \dfrac{kx}{x} \quad \color{Red} \text { Divide both sides by } x \\ \dfrac{F}{x}&= k \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Saying that \(F/x = k\) is equivalent to saying that \(k = F/x\). We can leave our answer in the form shown in the last step, but some instructors insist that we write the answer as follows:

\[k=\dfrac{F}{x} \quad \color{Red} \dfrac{F}{x}=k \text { is equivalent to } k=\dfrac{F}{x} \nonumber \]

Note that we have \(k = \text {“Stuff”}\), where “Stuff” contains no occurrence of \(k\), the variable we are solving for.

Exercise \(\PageIndex{3}\)

Solve for \(m : E=m c^{2}\).

Answer

\(m=\dfrac{E}{c^{2}}\)

Example \(\PageIndex{4}\)

The formula \(V = RI\) is called “Ohm’s Law.” It helps calculate the voltage drop \(V\) across a resistor \(R\) in an electric circuit with current \(I\). Solve the equation for \(R\).

Solution

We are instructed to solve the equation \(V = RI\) for \(R\). This means that our final answer must have the form \(R = \text {“Stuff”}\), where “Stuff” is a valid mathematical expression that may contain other variables, mathematical symbols, etc., but it may not contain any occurrence of the variable \(R\). This means that we must isolate all terms containing the variable \(R\) on one side of the equation, and all remaining terms on the other side of the equation. However, note that all terms containing the variable \(R\) are already isolated on one side of the equation. Terms not containing the variable R are isolated on the other side of the equation. Now, to “undo” the effect of multiplying by \(I\), divide both sides of the equation by \(I\).

\[\begin{aligned} V&= R I \quad \color{Red} \text { Original equation. } \\ \dfrac{V}{I}&=\dfrac{R I}{I} \quad \color{Red} \text { Divide both sides by } I \\ \dfrac{V}{I}&= R \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

This can also be written in the following form:

\[R=\dfrac{V}{I} \quad \color{Red} V / I=R \text { is equivalent to } R=V / I \nonumber \]

Note that we have \(R = \text {“Stuff”}\), where “Stuff” contains no occurrence of \(R\), the variable we are solving for.

Exercise \(\PageIndex{4}\)

Solve for \(t : d=s t\).

Answer

\(t=\dfrac{d}{s}\)

Clearing Fractions

If fractions occur in a formula, clear the fractions from the formula by multiplying both sides of the formula by the common denominator.

Example \(\PageIndex{5}\)

The formula \(K=\dfrac{1}{2} m v^{2}\) is used to calculate the kinetic energy \(K\) of a particle of mass \(m\) moving with velocity \(v\). Solve the equation for \(m\).

Solution

We’re asked to solve the equation \(K = (1 /2)mv^2\) for \(m\). First, clear the fractions by multiplying both sides by the common denominator.

\[\begin{aligned} K &= \dfrac{1}{2} mv^{2} \quad \color{Red} \text { Original equation. } \\ 2(K) &= 2\left(\dfrac{1}{2} mv^{2}\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2K &= mv^{2} \quad \color{Red} \text { Simplify. Cancel } 2^{\prime} \text { s. } \end{aligned} \nonumber \]

Note that all terms containing \(m\), the variable we are solving for, are already isolated on one side of the equation. We need only divide both sides by \(v^2\) to complete the solution.

\[\begin{aligned} \dfrac{2 K}{v^2}&= \dfrac{m v^{2}}{v^{2}} \quad \color{Red} \text { Divide both sides by } v^{2} \\ \dfrac{2 K}{v^2}&= m \quad \color{Red} \text { Simplify. Cancel } v^{2} \text { for } v^{2} \end{aligned} \nonumber \]

Note that the final answer has the form \(m = \text {“Stuff”}\), where “Stuff” contains no occurrence of the variable \(m\).

Exercise \(\PageIndex{5}\)

Solve for \(g : s=\dfrac{1}{2} g t^{2}\).

Answer

\(g=\dfrac{2 s}{t^{2}}\)

Example \(\PageIndex{6}\)

As mentioned earlier, Newton’s Universal Law of Gravitation is described by the formula \[F=\dfrac{G M m}{r^{2}} \nonumber \]Solve this equation for \(m\).

Solution

We’re asked to solve the equation \(F = GMm/r^2\) for \(m\). First, clear the fractions by multiplying both sides by the common denominator.

\[\begin{aligned} F &= \dfrac{G M m}{r^{2}} \quad \color{Red} \text { Original equation. } \\ r^{2}(F) &= r^{2}\left(\dfrac{G M m}{r^{2}}\right) \quad \color{Red} \text { Multiply both sides by } r^{2} \\ r^{2} F &= G M m \quad \color{Red} \text { Simplify. Cancel } r^{2} \text { for } r^{2} \end{aligned} \nonumber \]

Note that all terms containing \(m\), the variable we are solving for, are already isolated on one side of the equation. We need only divide both sides by \(GM\) to complete the solution.

\[\begin{aligned} \dfrac{r^{2} F}{G M}&= \dfrac{G M m}{G M} \quad \color{Red} \text { Divide both sides by } G M \\ \dfrac{r^{2} F}{G M}&= m \quad \color{Red} \text { Simplify. Cancel } G M \text { for } G M \end{aligned} \nonumber \]

Note that the final answer has the form \(m = \text {“Stuff”}\), where “Stuff” contains no occurrence of the variable \(m\).

Exercise \(\PageIndex{6}\)

Solve for \(q_{2} : F=\dfrac{k q_{1} q_{2}}{r^{2}}\).

Answer

\(q_{2}=\dfrac{F r^{2}}{k q_{1}}\)

Geometric Formulae

Let’s look at a few commonly used formulae from geometry.

Example \(\PageIndex{7}\)

Let \(W\) and \(L\) represent the width and length of a rectangle, respectively, and let \(P\) represent its perimeter.

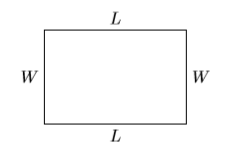
The perimeter (distance around) of the rectangle is found by summing its four sides, then combining like terms.

\[\begin{aligned} P&=L+W+L+W \quad \color{Red} \text { Summing the four sides. } \\ P&=2 W+2L \quad \color{Red} \text { Combine like terms. } \end{aligned} \nonumber \]

Solve \(P =2W +2L\) for \(L\). Then, given that the perimeter is \(300\) feet and the width is \(50\) feet, use your result to calculate the length.

Solution

We’re first asked to solve \(P =2W +2L\) for \(L\). First, isolate all terms containing the variable \(L\) on one side of the equation.

\[\begin{aligned} P&= 2W+2L \quad \color{Red} \text { Original equation. } \\ P-2W&= 2W+2L-2W \quad \color{Red} \text { Subtract } 2W \text { from both sides. } \\ P-2W&= 2L \quad \color{Red} \text { Simplify. } \\ \dfrac{P-2W}{2}&= \dfrac{2L}{2} \quad \color{Red} \text { Divide both sides by } 2 \\ \dfrac{P-2W}{2}&=L \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Note that the final result has \(L = \text {“Stuff"}\), where “Stuff” contains no occurrence of the variable \(L\).

The second part of this example requests that we find the length of the rectangle, given that the perimeter is \(P = 300\) feet and the width is \(W = 50\) feet. To calculate the length, substitute \(P = 300\) and \(W = 50\) in \(L =( P - 2W)/2\).

\[\begin{aligned} &L= \dfrac{P-2 W}{2} \quad \color{Red} \text { Perimeter formula solved for } L \\ L&= \dfrac{300-2(50)}{2} \quad \color{Red} 300 \text { for } P, 50 \text { for } W\\ L &= \dfrac{300-100}{2} \quad \color{Red} \text { Multiply: } 2(50)=100 \\ L &= \dfrac{200}{2} \quad \color{Red} \text { Subtract: } 300-100=200 \\ L &= 100 \quad \color{Red} \text { Divide: } 200 / 2=100 \end{aligned} \nonumber \]

Hence, the length of the rectangle is \(100\) feet.

Exercise \(\PageIndex{7}\)

The perimeter of a rectangle is \(160\) meters and its width is \(30\) meters. Finds its length.

Answer

\(L=50\) meters

Example \(\PageIndex{8}\)

Let \(b\) and \(h\) represent the length of the base and the height of a triangle, respectively, and let \(A\) represent the area of the triangle.

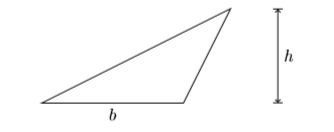
The area of the triangle is computed using the formula: \(A=\dfrac{1}{2} bh\)That is, the area of a triangle is “one-half the base times the height.”

Solve the formula \(A=\dfrac{1}{2} bh\) for \(h\). Secondly, given that the area is \(A = 90\) in² (\(90\) square inches) and the length of the base is \(15\) in (\(15\) inches), find the height of the triangle.

Solution

We’re first asked to solve \(A = (1 /2)bh\) for \(h\). Because the equation has fractions, the first step is to clear the fractions by multiplying both sides by the least common denominator.

\[\begin{aligned} A &= \dfrac{1}{2} bh \quad \color{Red} \text { Area of a triangle formula. } \\ 2(A) &= 2\left(\dfrac{1}{2} bh\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2A &= bh \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Now, we already have all terms containing the variable \(h\) on one side of the equation, so we can solve for \(h\) by dividing both sides of the equation by \(b\).

\[\begin{aligned} \dfrac{2 A}{b}&= \dfrac{b h}{b} \quad \color{Red} \text { Divide both sides by } b \\ \dfrac{2 A}{b}&= h \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Note that the final result has \(h = \text {“Stuff"}\), where “Stuff” contains no occurrence of the variable \(h\).

The second part of this example requests that we find the height of the triangle, given that the area is \(A = 90\) in \(2\) and the length of the base is \(b = 15\) in. To calculate the height of the triangle, substitute \(A = 90\) and \(b = 15\) in \(h =2A/b\).

\[\begin{aligned} h &= \dfrac{2 A}{b} \quad \color{Red} \text { Area formula solved for } h \\ h &= \dfrac{2(90)}{15} \quad \color{Red} \text {Substitue }90 \text { for } A, 15 \text { for } b\\ h &=\dfrac{180}{15} \quad \color{Red} \text { Multiply: } 2(90)=180 \\ h &= 12 \quad \color{Red} \text {Divide: } 180 / 15=12 \end{aligned} \nonumber \]

Hence, the height of the triangle is \(12\) inches.

Exercise \(\PageIndex{8}\)

The area of a triangle is \(140\) cm² and the length of its base is \(70\) cm. Find the height of the triangle. .

Answer

\(4\) cm