2.5: Applications

Last updated
Save as PDF

Page ID: 19860

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

The solution of a word problem must incorporate each of the following steps.

Requirements for Word Problem Solutions

Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let $P$ represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
Set up an Equation.Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
Solve the Equation. You must always solve the equation set up in the previous step.
Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units.
Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”

Let’s give these requirements a test drive.

Example $\PageIndex{1}$

Three more than ﬁve times a certain number is $-62$. Find the number.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $x$ represent the unknown number.
Set up an Equation.“Three more than ﬁve times a certain number is $-62$” becomes:

$fig 2.5.1a.png$

Solve the Equation. To solve for $x$, ﬁrst subtract $3$ from both sides of the equation.\[\begin{aligned} 3+5 x &= -62 \quad \color {Red} \text { Original equation. } \\ 3+5 x-3 &= -62-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides. } \\ 5x &= -65 \quad \color {Red} \text { Simplify. } \\ \dfrac{5 x}{5} &= \dfrac{-65}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ x &= -13 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. The unknown number is $-13$.
Look Back. Compute “three more than ﬁve times $-13$.” \[\begin{aligned} 3+5(-13) &=3+(-65) \\ &=-62 \end{aligned} \nonumber \]Hence, three more than ﬁve times $-13$ is $-62$, as required. Our solution is correct.

Exercise $\PageIndex{1}$

$27$ more than $5$ times a certain number is $-148$. What is the number?

Answer: $-35$

Example $\PageIndex{2}$

The sum of three consecutive integers is $-66$. Find the smallest of these three integers.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $k$ represent the smallest of three consecutive integers.
Set up an Equation. An example of three consecutive integers is $34$, $35$, and $36$. These are not the integers we seek, but they serve to help in the understanding of the problem. Note how each consecutive integer is one larger than the preceding integer. If $k$ is the smallest of three consecutive integers, then the next two consecutive integers are $k +1$ and $k +2$. The “sum of three consecutive integers is $-66$” becomes:

$fig 2.5.1b.png$

Solve the Equation. To solve for $k$, ﬁrst simplify the left-hand side of the equation by combining like terms. \[\begin{aligned} k+(k+1)+(k+2) &=-66 \quad \color {Red} \text { Original equation. }\\ 3k+3 &=-66 \quad \color {Red} \text { Combine like terms. }\\ 3k+3-3 &=-66-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides.}\\ 3k &=-69 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{-69}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=-23 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. The smallest of three consecutive integers is $-23$.
Look Back. If $k = -23$ is the smallest of three consecutive integers, then the next two consecutive integers are $-22$ and $-21$. Let’s check the sum of these three consecutive integers. \[-23+(-22)+(-21)=-66 \nonumber \] Hence, the sum of the three consecutive integers is $-66$, as required. Our solution is correct

Exercise $\PageIndex{2}$

The sum of three consecutive odd integers is $-225$. What are the integers?

Answer: $-77,-75,-73$

Example $\PageIndex{3}$

A carpenter cuts a board measuring $60$ inches in three pieces. The second piece is twice as long as the ﬁrst piece, and the third piece is three times as long as the ﬁrst piece. Find the length of each piece cut by the carpenter.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $L$ represent the length of the ﬁrst piece. Then the second piece, which is twice as long as the ﬁrst piece, has length $2L$. The third piece, which is three times as long as the ﬁrst piece, has length $3L$. Let’s construct a little table to help summarize the information provided in this problem.

Piece	Length (in)
First piece	L
Second piece	2L
Third piece	3L
Total length	60

Set up an Equation. As you can see in the table above, the second column shows that the sum of the three pieces is $60$ inches. In symbols:\[L+2 L+3 L=60 \nonumber \]
Solve the Equation. To solve for $L$, ﬁrst simplify the left-hand side of the equation by combining like terms. \[\begin{aligned} L+2 L+3 L &= 60 \quad \color {Red} \text { Original equation. } \\ 6L &= 60 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{6L}{6} &= \dfrac{60}{6} \quad \color {Red} \text { Divide both sides by } 6 \\ L &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. The ﬁrst piece has length L = 10 inches. The second piece has length 2L = 20 inches. The third piece has length 3L = 30 inches. In tabular form, this is even more apparent.

Piece	Length (in)	Length(in)
First piece	L	10
Second piece	2L	20
Third piece	3L	30
Total length	60	60

Look Back. Not only is the second length twice the ﬁrst and the third length three times the ﬁrst, check the sum of their lengths: \[10+20+30=60 \nonumber \] That’s a total of $60$ inches. We have the correct solution.

Exercise $\PageIndex{3}$

Han cuts a board measuring $230$ inches in three pieces. The second piece is twice as long as the ﬁrst piece, and the third piece is $30$ inches longer than the second piece. Find the length of each piece cut by Han.

Answer: $40,80,110$ in

Example $\PageIndex{4}$

The three sides of a triangle are consecutive even integers. If the perimeter (sum of the three sides) of the triangle is $156$ centimeters, ﬁnd the length of each side of the triangle.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. An example of three consecutive even integers is $18$, $20$, and $22$. These are not the integers we seek, but they do give us some sense of the meaning of three consecutive even integers. Note that each consecutive even integer is two larger than the preceding integer. Thus, if $k$ is the length of the ﬁrst side of the triangle, then the next two sides are $k+2$ and $k+4$. In this example, our variable dictionary will take the form of a well-labeled ﬁgure.

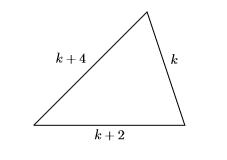
$fig 2.5.1c.png$

Set up an Equation. The perimeter of the triangle is the sum of the three sides. If the perimeter is $156$ centimeters, then: \[k+(k+2)+(k+4)=156 \nonumber \]
Solve the Equation. To solve for k, ﬁrst simplify the left-hand side of the equation by combining like terms. \[\begin{aligned} k+(k+2)+(k+4) &=156 \quad \color {Red} \text { Original equation. }\\ 3k+6 &=156 \quad \color {Red} \text { Combine like terms. }\\ 3k+6-6 &=156-6 \quad \color {Red} \text { Subtract } 6 \text { from both sides.}\\ 3k &=150 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{150}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=50 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. Thus, the ﬁrst side has length $50$ centimeters. Because the next two consecutive even integers are $k+2=52$ and $k+4= 54$, the three sides of the triangle measure $50$, $52$, and $54$ centimeters, respectively.
Look Back. An image helps our understanding. The three sides are consecutive even integers.

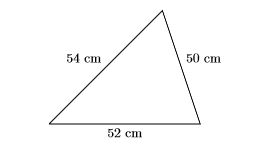
$fig 2.5.1d.png$

Note that the perimeter (sum of the three sides) is: \[50 \mathrm{cm}+52 \mathrm{cm}+54 \mathrm{cm}=156 \mathrm{cm} \nonumber \] Thus, the perimeter is $156$ centimeters, as it should be. Our solution is correct.

Exercise $\PageIndex{4}$

The three sides of a triangle are consecutive integers. If the perimeter (sum of the three sides) of the triangle is $453$ centimeters, ﬁnd the length of each side of the triangle.

Answer: $150,151,152 $ cm

Example $\PageIndex{5}$

A well-known fact from geometry is the fact that the sum of the angles of a triangle is $180^{\circ}$. Suppose we have a triangle whose second angle is $10$ degrees larger than twice its ﬁrst angle and whose third angle is $50$ degrees larger than its ﬁrst angle. Find the measure of each angle of the triangle.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. The Greek alphabet starts out with the letters $\alpha, \beta, \gamma, \delta, \epsilon, \ldots,$ in much the same way that the English alphabet start out with the letters $a, b, c, d, e, \ldots$ Mathematicians love to use Greek letters, especially in the study of trigonometry. The greek letter $\theta$ (pronounced “theta”) is particularly favored in representing an angle of a triangle. So, we’ll let $\theta$ represent the degree measure of the ﬁrst angle of the triangle. The second angle is $10$ degrees larger than twice the ﬁrst angle, so the second angle is $2\theta+10$. The third angle is $50$ degrees larger than the ﬁrst angle, so the third angle is $\theta+50$. Again, we’ll set up a well-labeled ﬁgure for our variable dictionary.

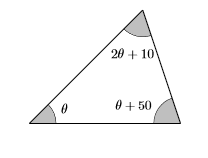
$fig 2.5.1e.png$

Set up an Equation. The sum of the angles is $180^{\circ}$, so: \[\theta+(2 \theta+10)+(\theta+50)=180 \nonumber \]
Solve the Equation. To solve for $\theta$, ﬁrst simplify the left-hand side of the equation by combining like terms.\[\begin{aligned} \theta+(2 \theta+10)+(\theta+50) & =180 \quad \color {Red} \text { Original equation. }\\ 4 \theta+60 & =180 \quad \color {Red} \text { Combine like terms. }\\ 4 \theta+60-60 & =180-60 \quad \color {Red} \text { Subtract } 60 \text { from both sides.}\\ 4 \theta & =120 \quad \color {Red} \text { Simplify. }\\ \dfrac{4 \theta}{4} & =\dfrac{120}{4} \quad \color {Red} \text { Divide both sides by } 4.\\ \theta & =30 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. Thus, the ﬁrst angle is $\theta=30$ degrees, the second angle is $2\theta+10=70$ degrees, and the third angle is $\theta+50=80$ degrees.
Look Back. An image helps our understanding. Note that the second angle is 10 degrees larger than twice the ﬁrst angle. Note that the third angle is $50$ degrees larger than the ﬁrst angle.

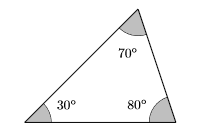
$fig 2.5.1f.png$

Note that the sum of the angles is: \[30^{\circ}+70^{\circ}+80^{\circ}=180^{\circ} \nonumber \] Thus, the sum of the three angles is 180 degrees, as it should be. We have the correct solution.

Exercise $\PageIndex{5}$

The second angle of a triangle is three times bigger than the ﬁrst angle. The third angle of the triangle is a $40$ degrees larger than the second angle. How many degrees are in each angle?

Answer: $20^{\circ}, 60^{\circ}, 100^{\circ}$

Example $\PageIndex{6}$

Martha inherits $\$21,000$ and decides to invest the money in three separate accounts. The amount she invests in the second account is twice the amount she invests in the ﬁrst account. The amount she invests in the third account is $\$1,000$ more than the amount she invests in the second account. How much did she invest in each account?

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. We’ll use a table in this example to help set up our variable dictionary. Let $x$ be the amount invested in the ﬁrst account. The amount invested in the second account is twice that invested in the ﬁrst account, so $2x$ is the amount invested in the second account. The third account investment is $\$1,000$ more than the amount invested in the second account, so that is $2x + 1000$.

Account #	Amount Invested
Account#1	x
Account#2	2x
Account#3	2x+1000
Total Invested	21000

Set up an Equation. The second column of the table reveals the required equation. The three investments must sum to $\$21,000$.\[x+2 x+(2 x+1000)=21000 \nonumber \]
Solve the Equation. To solve for $x$, ﬁrst simplify the left-hand side of the equation by combining like terms.\[\begin{aligned} x+2 x+(2 x+1000) &=21000 \quad \color {Red} \text { Original equation. }\\ 5 x+1000 &=21000 \quad \color {Red} \text { Combine like terms. }\\ 5 x+1000-1000 &=21000-1000 \quad \color {Red} \text { Subtract } 1000 \text { from both sides.}\\ 5 x &=20000 \quad \color {Red} \text { Simplify. }\\ \dfrac{5 x}{5} &=\dfrac{20000}{5} \quad \color {Red} \text { Divide both sides by } 5.\\ x &=4000 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. Substitute $x = 4000$ in each entry of the second column of the table above to produce the results in the table below.

Account #	Amount Invested	Amount Invested
Account#1	x	$4,000
Account#2	2x	$8,000
Account#3	2x+1000	$9,000
Total Invested	21000	$21,000

Look Back. As we can see in our answer table, the amount $\$8,000$ invested in the second account is twice the amount invested in the ﬁrst account. The amount $\$9,000$ invested in the third account is $\$1,000$ more than the amount invested in the second account. Moreover, the total investment is: \[\$ 4,000+\$ 8,000+\$ 9,000=\$ 21,000 \nonumber \]Thus, the total investment is $\$21,000$, as it should be. We have the correct solution.

Exercise $\PageIndex{6}$

Jim inherits $\$15,000$. He invests part in a fund that pays $5\%$ per year and the rest in a fund that pays $4\%$ per year. At the end of one year, the combined interest from both investments was $\$4,250$. How much did he invest in each fund?

Answer: $\$ 5,000$ at $5\%$ and $\$ 10,000$ at $4\% $.

Example $\PageIndex{7}$

Jeﬀ is hiking the $2,650$-mile Paciﬁc Crest Trail from Mexico to Canada. Shortly before he crosses over from Oregon into Washington he is four times as far from the beginning of the trail as he is from the end. How much further does he have to hike?

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $d$ represent the distance left for Jeﬀ to hike. Because Jeﬀ is four times further from the beginning of the trail than the end, the distance Jeﬀ already completed is $4d$. Let’s construct a little table to help summarize the information provided in this problem.

Section of Trail	Distance (mi)
Distance to ﬁnish	d
Distance from start	4d
Total distance	2650

Set up an Equation. As you can see in the table above, the second column shows that the sum of the two distances is $2650$ miles. In symbols: \[d+4 d=2650 \nonumber \
Solve the Equation. To solve for $d$, ﬁrst simplify the left-hand side of the equation by combining like terms. \[\begin{aligned} d+4d & =2650 \quad \color {Red} \text { Original equation. } \\ 5d & =2650 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{5d}{5} & =\dfrac{2650}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ d & =530 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. Jeﬀ still has $530$ miles to hike.
Look Back. Because the amount left to hike is $d = 530$ miles, Jeﬀ’s distance from the start of the trail is $4d = 4(530)$, or $2,120$ miles. If we arrange these results in tabular form, it is evident that not only is the distance from the start of the trail four times that of the distance left to the ﬁnish, but also the sum of their lengths is equal to the total length of the trail.

Section of Trail	Distance (mi)	Distance (mi)
Distance to ﬁnish	d	530
Distance from start	4d	2120
Total distance	2650	2650

Thus, we have the correct solution.

Exercise $\PageIndex{7}$

Margaret is cycling along a lane that measures $100$ miles. If Magaret is four times as far from the start of the ride as she is from the ﬁnish, how many more miles does she have to go before she ﬁnishes her ride?

Answer: $20$ miles

Example $\PageIndex{8}$

Today $15\%$ of Sister Damaris’ seventh grade class were ill and stayed home from school. If only $34$ students are present, what is the actual size of Sister Damaris’ class?

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $S$ represent the actual size of Sister Damaris’ class.
Set up an Equation. If $15\%$ of Sister Damaris’ class was absent, then $85\%$ of her class was present. There are $34$ student present, so the phrase “$85\%$ of Sister Damaris’ class is $34$” translates into the equation, \[0.85 S=34 \nonumber \]where we’ve changed $85\%$ to a decimal by moving the decimal point two places to the left.
Solve the Equation. To solve for $S$, ﬁrst clear the decimals by multiplying both sides of the equation by $100$. \[\begin{aligned} 0.85S &= 34 \quad \color {Red} \text { Original equation. } \\ 85S &= 3400 \quad \color {Red} \text { Multiply both sides by } 100. \\ \dfrac{85S}{85}&= \dfrac{3400}{85} \quad \color {Red} \text { Divide both sides by } 85 \\ S&= 40 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Answer the Question. Sister Damaris’ class size is $40$.
Look Back. We’re told that $15\%$ of Sister Damaris’ class is absent. If we calculate $15\%$ of $40$, we get: \[0.15(40)=6 \nonumber \] Thus, there were 6 students absent, so $40-6$, or $34$ students were present. Thus, we have the correct solution.

Exercise $\PageIndex{8}$

$20\%$ of Mary’s class were ill and stayed home from school. If only $36$ students are present, what is the actual size of Mary’s class?

Answer: $45$

Search

Text Color

Text Size

Margin Size

Font Type