2.1: Solving Equations - One Step

Let’s start with the definition of an equation.

Equation

An equation is a mathematical statement that equates two algebraic expressions.

The key difference between a algebraic expression and an equation is the presence of an an equals sign. So, for example,

$$2 x+3, \quad x-(3-2 x), \quad \text { and } \quad 2(y+3)-3(1-y) \nonumber$$

are algebraic expressions, while

$$2 x+3=0, \quad x-(3-2 x)=4, \quad \text { and } \quad 2(y+3)-3(1-y)=-11 \nonumber$$
are equations. Note that each of the equations contain an equals sign, but the algebraic expressions do not.

Next we have the definition of a solution of an equation.

What it Means to be a Solution of an Equation

A solution of an equation is a numerical value that satisfies the equation. That is, when the variable in the equation is replaced by the solution, a true statement results.

Example $\PageIndex{1}$

Show that $8$ is a solution of the equation $x-12 = -4$.

Solution

Substitute $8$ for $x$ in the given equation and simplify.

$$\begin{aligned} x-12&=-4 \quad \color{Red} \text { The given equation. } \\ 8-12&=-4 \quad \color{Red} \text { Substitute } 8 \text { for } x . \\ -4&=-4 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Since the left- and right-hand sides of the last line are equal, this shows that when $8$ is substituted for $x$ in the equation a true statement results. Therefore, $8$ is a solution of the equation

Exercise $\PageIndex{1}$

Which of the numbers $\{1,2,3,4,5\}$ is a solution of the equation $2 y+3=7$.

Answer

$2$

Equivalent Equations

Now that we know how to identify a solution of an equation, let’s define what it means when we say that two equations are equivalent.

Equivalent Equations

Two equations are equivalent if they have the same solution set.

Example $\PageIndex{2}$

Are the equations $x-3 = 6$ and $x = 9$ equivalent?

Solution

The number $9$ is the only solution of the equation $x − 3 = 6$. Similarly, $9$ is the only solution of the equation $x = 9$. Therefore $x−3 = 6$ and $x = 9$ have the same solution sets and are equivalent.

Exercise $\PageIndex{2}$

Are the equations $x = 5$ and $x-7 = 10$ equivalent?

Answer

No

Example $\PageIndex{3}$

Are the equations $x^2 = 1$ and $x = 1$ equivalent?

Solution

By inspection, the equation $x^2 = 1$ has two solutions, $-1$ and $1$.

$(-1)^{2}=1 \quad$ and $\quad(1)^{2}=1$

On the other hand, the equation $x = 1$ has a single solution, namely $1$. Hence, the equations $x^2 = 1$ and $x = 1$ do not have the same solution sets and are not equivalent.

Exercise $\PageIndex{3}$

Are the equations $x = 1$ and $x^2 = x$ equivalent?

Answer

No

As we shall soon see, equivalent equations play an important role in finding the solution of an equation.

Wrap and Unwrap, Do and Undo

Suppose that you are wrapping a gift for your cousin. You perform the following steps in order.

1. Put the gift paper on.
2. Put the tape on.
3. Put the decorative bow on.

When we give the wrapped gift to our cousin, he politely unwraps the present, “undoing” each of our three steps in inverse order.

1. Take off the decorative bow.
2. Take off the tape.
3. Take off the gift paper.

This seemingly frivolous wrapping and unwrapping of a gift contains some deeply powerful mathematical ideas. Consider the mathematical expression $x + 4$. To evaluate this expression at a particular value of $x$, we would start with the given value of $x$, then add $4$.

• Let’s set $x$ equal to the number $7$. If we add $4$, we arrive at the following result: $11$

Now, how would we “unwrap” this result to return to our original number? We would start with our result, namely $11$, then subtract $4$.

• Take our result from above, $11$. If we subtract $4$, we return to our original value of $x$: $7$

The above discussion leads us to two extremely important observations.

Note

The inverse of addition is subtraction. If we start with a number $x$ and add a number $a$, then subtracting $a$ from the result will return us to the original number $x$. In symbols,

$x + a - a = x$

That is, subtracting $a$ “undoes” the effect of adding $a$ and returns us to the original number $x$.
The inverse of subtraction is addition. If we start with a number $x$ and subtract a number $a$, then adding $a$ to the result will return us to the original number $x$. In symbols,

$x - a + a = x$

That is, adding $a$ “undoes” the effect of subtracting $a$ and returns us to the original number $x$.

Operations that Produce Equivalent Equations

In Example $\PageIndex{1}$, we saw that $x = 8$ was a solution of the equation $x-12 = -4$. Indeed, the equations $x = 8$ and $x-12 = -4$ are equivalent equations because both have the same solution sets.

In the case of the equation $x-12 = -4$, it’s fairly easy to “guess” that the solution is $x = 8$, but as the equations become more complicated, we will want to know just what operations we can perform on the equation that will not change the solution set. The goal is to start with an equation such as

$x-12 = -4$

then through a series of steps that do not change the solution, arrive at the solution

$x =8$

With these thoughts in mind, there are a number of operations that will produce equivalent equations (equations with the same solution set). The first two that we will employ are adding or subtracting the same amount from both sides of an equation.

Adding the Same Quantity to Both Sides of an Equation

Adding the same quantity to both sides of an equation does not change the solution set. That is, if

$a = b$

then adding $c$ to both sides of the equation produces the equivalent equation

$a + c = b + c$

Subtracting the Same Quantity from Both Sides of an Equation

Subtracting the same quantity to both sides of an equation does not change the solution set. That is, if

$a = b$

then subtracting c from both sides of the equation produces the equivalent equation

$a-c = b-c$

Let’s look at an example where adding the same amount to both sides of the equation produces an equivalent equation that is the solution to the original equation.

Example $\PageIndex{4}$

Solve $x-7 = 12$ for $x$.

Solution

To undo the effect of subtracting $7$, we add $7$ to both sides of the equation.

$$\begin{aligned} x-7&=12 \quad \color{Red} \text { Original equation. } \\ x-7+7&=12+7 \quad \color{Red} \text { Adding } 7 \text { to both sides of the equation produces an equivalent equation. } \\ x&=19 \quad \color{Red} \text { On the left, adding } 7 \text { "undoes" the effect of subtracting } 7 \text { and returns } x . \text { On the right, } 12+7=19 \end{aligned} \nonumber$$

Therefore, the solution of the equation is $19$.

Check: To check, substitute the solution $19$ into the original equation.

$$\begin{aligned} x-7&=12 \quad \color{Red} \text { Original equation. } \\ 19-7&=12 \quad \color{Red} \text { Substitute } 19 \text { for } x \\ 12&=12 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

The fact that the last line of the check is a true statement guarantees that $19$ is a solution of $x-7 = 12$.

Exercise $\PageIndex{4}$

Solve for $x : x-6=4$.

Answer

$10$

In the solution of Example $\PageIndex{4}$, we use the concept of the “inverse.” If we start with $x$, subtract $7$, then add $7$, we are returned to the number $x$. In symbols, $x-7+7=x$. We are returned to x because “subtracting $7$” and “adding $7$” are inverse operations of one another. That is, whatever one does, the other “undoes.”

Next, let’s look at an example where subtracting the same amount from both sides of the equation produces an equivalent equation that is the solution to the original equation.

Example $\PageIndex{5}$

Solve $x+\dfrac{2}{3}=\dfrac{1}{2}$ for $x$.

Solution

To undo the effect of adding $2/3$, we subtract $2/3$ from both sides of the equation.

$$\begin{aligned} x+\dfrac{2}{3}&=\dfrac{1}{2} \quad \color{Red} \text { Original equation. } \\ x+\dfrac{2}{3}-\dfrac{2}{3}&=\dfrac{1}{2}-\dfrac{2}{3} \quad \color{Red} \text { Subtracting } 2 / 3 \text { from both sides produces an equivalent equation.} \\ x&=\dfrac{3}{6}-\dfrac{4}{6} \color{Red} \text { On the left, subtracting } 2/3 \text { "undoes" the effect of adding } 2/3 \text { and returns } x \text{. On the right, make equivalent fractions with a common denominator.}\\ x&=-\dfrac{1}{6} \quad \color{Red} \text { Subtract: } \dfrac{3}{6}-\dfrac{4}{6}=-\dfrac{1}{6} \end{aligned} \nonumber$$

Therefore, the solution of the equation is $-1/6$.

Check: Let’s use the TI-84 graphing calculator to check this solution.

1. Store the value $-1/6$ in the variable $X$ using the following keystrokes. The result is shown in Figure $\PageIndex{1}$.

2. Enter the left-hand side of the original equation: x +2 /3. Use the following keystrokes. The result is shown in Figure 2.1.

Figure $\PageIndex{1}$: Checking the solution to $x +2/3=1 /2$.

3. Press the MATH button on your calculator (see Figure $\PageIndex{2}$), then select 1:Frac and press the ENTER button. This will convert the decimal result to a fraction (see Figure $\PageIndex{2}$).

Figure $\PageIndex{2}$: Changing the result to a fraction.

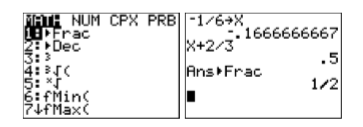
Note that the result is $\dfrac{1}{2},$ showing that $-\dfrac{1}{6}$ is a solution of $x+\dfrac{2}{3}=\dfrac{1}{2}$.

Exercise $\PageIndex{5}$

Solve for $x : x+\dfrac{1}{2}=\dfrac{3}{5}$.

Answer

$1/10$

More Operations That Produce Equivalent Equations

Here are two more operations that produce equivalent equations.

Multiplying Both Sides of an Equation by a Nonzero Quantity

Multiplying both sides of an equation by a nonzero quantity does not change the solution set. That is, if

$a = b$

and $c \neq 0$, then multiplying both sides of the equation by $c$ produces the equivalent equation

$ac = bc$

Dividing Both Sides of an Equation by a Nonzero Quantity

Dividing both sides of an equation by a nonzero quantity does not change the solution set. That is, if

$a = b$

and $c \neq 0$, then dividing both sides of the equation by $c$ produces the equivalent equation

$\dfrac{a}{c}=\dfrac{b}{c}$

Like addition and subtraction, multiplication and division are inverse operations.

Note

The inverse of multiplication is division. If we start with a number $x$ and multiply by a number $a$, then dividing the result by the same number $a$ returns us to the original number $x$. In symbols,

$\dfrac{a \cdot x}{a}=x$

That is, dividing by a “undoes” the effect of multiplying by $a$ and returns us to the original number $x$.

The inverse of division is multiplication. If we start with a number $x$ and divide by a number $a$, then multiplying the result by the same number $a$ returns us to the original number $x$. In symbols,

$a \cdot \dfrac{x}{a}=x$

That is, multiplying by a “undoes” the effect of dividing by $a$ and returns us to the original number $x$.

Let’s look at an example where dividing both sides of the equation by the same amount produces an equivalent equation that is the solution to the original equation.

Example $\PageIndex{6}$

Solve $-2.1 x=0.42$ for $x$.

Solution

To undo the effect of multiplying by $-2.1$, we divide both sides of the equation by $-2.1$.

$$\begin{aligned} -2.1 x &=0.42 \quad \color{Red} \text {Original equation.}\\ \frac{-2.1 x}{-2.1} &=\frac{0.42}{-2.1} \quad \color{Red} \text {Dividing both sides by } -2.1 \text{ produces an equivalent equation.}\\ x &=-2 \quad \color{Red} \text {On the left, dividing by } -2.1 \text {"undoes" the effect of multiplying by } -2.1 \text { and returns } x. \text {On the right, divide: } 0.42 /(-2.1)=-2 \end{aligned} \nonumber$$

Therefore, the solution of the equation is $-2$.

Check: To check, substitute the solution $-2$ into the original equation.

$$\begin{aligned} -2.1 x&=0.42 \quad \color{Red} \text { Original equation. } \\ -2.1(-2)&=0.42 \quad \color{Red} \text { Substitute }-2 \text { for } x \\ 0.42&=0.42 \quad \color{Red} \text { On the left, multiply: }-2.1(-2)=0.42 \end{aligned} \nonumber$$

The fact that the last line of the check is a true statement guarantees that $-2$ is a solution of $-2.1x =0.42$.

Exercise $\PageIndex{6}$

Solve for $x : -3.6 x = 0.072$.

Answer

$-0.02$

Next, lets look at an example where multiplying both sides of the equation by the same amount produces an equivalent equation that is the solution to the original equation.

Example $\PageIndex{7}$

Solve $\dfrac{x}{5}=-10$ for $x$.

Solution

To undo the effect of dividing by $5$, we multiply both sides of the equation by $5$.

$$\begin{aligned} \dfrac{x}{5} &=-10 \quad \color{Red} \text {Original equation.} \\ 5\left[\dfrac{x}{5}\right] &=[-10] 5 \quad \color{Red} \text {Multiplying both sides by } 5 \text {produces an equivalent equation.} \\ x &=-50 \quad \color{Red} \text {On the left, multiplying by } 5 \text { "undoes" the effect of dividing by } 5 \text { and returns } x \text {. On the right, multiply: } [-10 ] 5=-50 \end{aligned} \nonumber$$

Therefore, the solution of the equation is $-50$.

Check: Let’s use the TI-84 graphing calculator to check this solution.

1. Store the value $-50$ in the variable $X$ using the following keystrokes. The result is shown in Figure $\PageIndex{3}$.

2. Enter the left-hand side of the original equation:$\frac{x}{5}$. Use the following keystrokes.

Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: Checking the solution to $x/5=-10$.

Note that the result is $-10$, showing that $-50$ is a solution of $x/5=-10$.

Exercise $\PageIndex{7}$

Solve for $x: \dfrac{x}{7}=-2$.

Answer

$-14$

Writing Mathematics

When solving equations, observe the following rules when presenting your work.

1. One equation per line. This means that you should not arrange your work horizontally as follows: $$x+3=7 \quad x+3-3=7-3 \quad x=4 \nonumber$$ That’s three equations on a line. Instead, work vertically, writing one equation per line. In the following presentation, note how we align the equal signs in a column. $$\begin{aligned} x+3 &=7 \\ x+3-3 &=7-3 \\ x &=4 \end{aligned} \nonumber$$
2. Add and subtract inline. Do not add $7$ to both sides of the equation in the following manner: $$\begin{array}{r}{x-7=12} \\ {+7\;\;\;+7} \\ \hline x=19\end{array} \nonumber$$ Instead, add $7$ “inline” to both sides of the equation as follows: $$\begin{aligned} x-7 &=12 \\ x-7+7 &=12+7 \\ x &=19 \end{aligned} \nonumber$$