3.6: Standard Form of a Line

In this section we will investigate the standard form of a line. Let’s begin with a simple example.

Example \(\PageIndex{1}\)

Solve the equation \(2x +3y = 6\) for \(y\) and plot the result.

Solution

First we solve the equation \(2x +3y = 6\) for \(y\). Begin by isolating all terms containing y on one side of the equation, moving or keeping all the remaining terms on the other side of the equation.

\[\begin{aligned} 2x+3y &= 6 \quad \color{Red} \text { Original equation. } \\ 2x+3y-2x &= 6-2x \quad \color{Red} \text { Subtract } 2x \text { from both sides. } \\ 3y &= 6-2x \quad \color{Red} \text { Simplify. } \\ \dfrac{3y}{3} &= \dfrac{6-2x}{3} \quad \color{Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]

Note

Just as multiplication is distributive with respect to addition \[a(b + c)=ab + ac \nonumber \]so too is division distributive with respect to addition.\[\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

When dividing a sum or a difference by a number, we use the distributive property and divide both terms by that number.

\[\begin{aligned} y &= \dfrac{6}{3}-\dfrac{2x}{3} \quad \color{Red} \text { On the left, simplify. On the right, divide both terms by } 3 \\ y &= 2-\dfrac{2 x}{3} \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Finally, use the commutative property to switch the order of the terms on the right-hand side of the last result.

\[\begin{aligned} y &= 2+\left(-\dfrac{2 x}{3}\right) \quad \color{Red} \text { Add the opposite. } \\ y &= -\dfrac{2}{3} x+2 \quad \color{Red} \text { Use the commutative property to switch the order. } \end{aligned} \nonumber \]

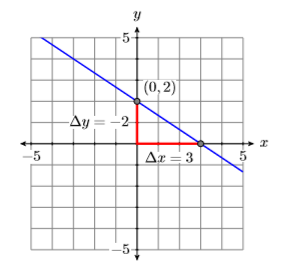
Because the equation \(2x +3y = 6\) is equivalent to the equation \(y=-\dfrac{2}{3} x+2\), the graph of \(2x +3 y = 6\) is a line, having slope \(m = −2/3\) and \(y\)-intercept \((0 ,2)\). Therefore, to draw the graph of \(2x+3y = 6\), plot they-intercept \((0,2)\), move down \(2\) and \(3\) to the right, then draw the line (see Figure \(\PageIndex{1}\) ).

Figure \(\PageIndex{1}\): The graph of \(2x +3y = 6\), or equivalently, \(y=-\dfrac{2}{3} x+2\)

Exercise \(\PageIndex{1}\)

Add exercises text here.

Answer

In general, unless \(B = 0\), we can always solve the equation \(Ax + By = C\) for y:

\[\begin{aligned}
Ax+By &= C \quad \color{Red} \text { Original equation. } \\
Ax+By-Ax &= C-Ax \quad \color{Red} \text { Subtract } Ax \text { from both sides. } \\
By &= C-Ax \quad \color{Red} \text { Simplify. } \\
\dfrac{By}{B} &= \dfrac{C-Ax}{B} \quad \color{Red} \text { Divide both sides by } B \\
y &= \dfrac{C}{B}-\dfrac{Ax}{B} \quad \color{Red} \text { distribute the } B \\
y &= -\dfrac{A}{B}x+\dfrac{C}{B} \quad \color{Red} \text { Commutative property }
\end{aligned} \nonumber \]

Note that the last result is in slope-intercept form \(y = mx+b\), whose graph is a line. We have established the following result.

FAct

The graph of the equation \(Ax + By = C\), is a line.

Important points: A couple of important comments are in order.

1. The form \(Ax + By = C\) requires that the coefficients \(A\), \(B\), and \(C\) are integers. So, for example, we would clear the fractions from the form \[\dfrac{1}{2} x+\dfrac{2}{3} y=\dfrac{1}{4} \nonumber \]by multiplying both sides by the least common denominator. \[\begin{aligned} 12\left(\dfrac{1}{2} x+\dfrac{2}{3} y\right) &=\left(\dfrac{1}{4}\right) 12 \\ 6 x+8 y &=3 \end{aligned}\nonumber \]Note that the coefficients are now integers.
2. The form \(Ax + By = C\) also requires that the first coefficient \(A\) is nonnegative; i.e., \(A ≥0\). Thus, if we have \[-5 x+2 y=6 \nonumber \]then we would multiply both sides by \(−1\), arriving at: \[\begin{aligned}-1(-5 x+2 y) &=(6)(-1) \\ 5 x-2 y &=-6 \end{aligned} \nonumber \]Note that \(A = 5\) is now greater than or equal to zero.
3. If \(A\), \(B\), and \(C\) have a common divisor greater than \(1\), it is recommended that we divide both sides by the common divisor, thus “reducing” the coefficients. For example, if we have \[3x + 12y =−24 \nonumber \]then dividing both side by \(3\) “reduces” the size of the coefficients.\[\begin{aligned} \dfrac{3 x+12 y}{3} &=\dfrac{-24}{3} \\ x+4 y &=-8 \end{aligned} \nonumber \]

Standard form

The form \(Ax + By = C\), where \(A\), \(B\), and \(C\) are integers, and \(A ≥ 0\), is called the standard form of a line.

Slope-Intercept to Standard Form

We’ve already transformed a couple of equations in standard form into slopeintercept form. Let’s reverse the process and place an equation in slope intercept form into standard form.

Example \(\PageIndex{2}\)

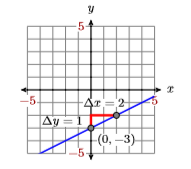
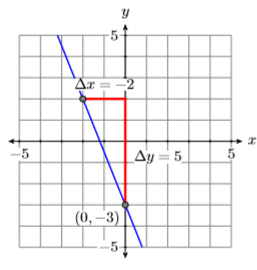
Given the graph of the line in Figure \(\PageIndex{2}\), find the equation Given the graph of the line below, find the equation of the line in standard form.

Figure \(\PageIndex{2}\): Determine the equation of the line.

Solution

The line intercepts the \(y\)-axis at \((0,−3)\). From \((0,−3)\), move up \(5\) units, then left \(2\) units. Thus, the line has slope \(\Delta y / \Delta x=-5 / 2\) (see Figure \(\PageIndex{3}\)). Substitute \(−5/2\) form and \(−3\) for \(b\) in the slope-intercept form of the line.

Figure \(\PageIndex{3}\): The line has \(y\)-intercept \((0,−3)\) and slope \(−5/2\).

\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= -\dfrac{5}{2} x-3 \quad \color{Red} \text { Substitute: }-5 / 2 \text { for } m,-3 \text { for } b \end{aligned} \nonumber \]

To put this result in standard form \(Ax + By = C\), first clear the fractions by multiplying both sides by the common denominator.

\[\begin{aligned} 2y &= 2\left[-\dfrac{5}{2} x-3\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y &= 2\left[-\dfrac{5}{2} x\right]-2[3] \quad \color{Red} \text { Distribute the } 2 \\ 2y &= -5x-6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

That clears the fractions. To put this last result in the form \(Ax+By = C\), we need to move the term \(−5x\) to the other side of the equation.

\[\begin{aligned} 5x+2y &= -5x-6+5x \quad \color{Red} \text { Add } 5x \text { to both sides. } \\ 5x+2y &= -6 \quad \color{Red}\text { Simplify. } \end{aligned} \nonumber \]

Thus, the standard form of the line is \(5x +2y = −6\). Note that all the coefficients are integers and the terms are arranged in the order \(Ax+By = C\), with \(A ≥0\).

Exercise \(\PageIndex{2}\)

Given the graph of the line below, find the equation of the line in standard form.

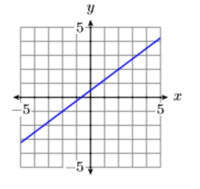
Answer

\(3 x−4y = −2\)

Point-Slope to Standard Form

Let’s do an example where we have to put the point-slope form of a line in standard form.

Example \(\PageIndex{3}\)

Sketch the line passing through the points \((−3,−4)\) and \((1,2)\), then find the equation of the line in standard form.

Solution

Plot the points (−3,−4) and (1,2), then draw a line through them (see Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{4}\): The line through \((−3,−4)\) and \((1,2)\).

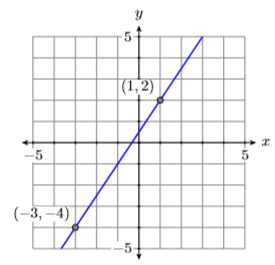
Use the points \((−3,−4)\) and \((1,2)\) to calculate the slope.

\[\begin{aligned} \text { Slope } &= \dfrac{\Delta y}{\Delta x} \quad \color{Red} \text { Slope formula. } \\ &= \dfrac{2-(-4)}{1-(-3)} \quad \color{Red} \text { Subtract coordinates of }(-3,-4) \\ &= \dfrac{6}{4} \quad \text { Simplify. } \\ &= \dfrac{3}{2} \quad \text { Reduce. } \end{aligned} \nonumber \]

Let’s substitute \(\left(x_{0}, y_{0}\right)=(1,2)\) and \(m =3 /2\) in the point-slope form of the line. (Note: Substituting \(\left(x_{0}, y_{0}\right)=(-3,-4)\) and \(m =3 /2\) would yield the same answer.)

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-2 &= \dfrac{3}{2}(x-1) \quad \color{Red} \text { Substitute: } 3 / 2 \text { for } m, 1 \text { for } x_{0} \end{aligned} \nonumber \]

The question requests that our final answer be presented in standard form. First we clear the fractions.

\[\begin{aligned} y-2 &= \dfrac{3}{2} x-\dfrac{3}{2} \quad \color{Red} \text { Distribute the } 3 / 2 \\ 2[y-2] &= 2\left[\dfrac{3}{2} x-\dfrac{3}{2}\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y-2[2] &= 2\left[\dfrac{3}{2} x\right]-2\left[\dfrac{3}{2}\right] \quad \color{Red} \text { Distribute the } 2 \\ 2y-4 &= 3 x-3 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Now that we’ve cleared the fractions, we must order the terms in the form \(Ax+By = C\). We need to move the term \(3x\) to the other side of the equation.

\[\begin{aligned} 2y-4-3x &= 3x-3-3x \quad \color{Red} \text { Subtract } 3 x \text { from both sides. } \\ -3x+2y-4 &= -3 \quad \color{Red} \text { Simplify, changing the order on the left-hand side. } \end{aligned} \nonumber \]

To put this in the form \(Ax + By = C\), we need to move the term \(−4\) to the other side of the equation.

\[\begin{aligned} -3x+2y-4+4 &= -3+4 \quad \color{Red} \text { Add } 4 \text { to both sides. } \\ -3x+2y &= 1 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

It appears that \(−3x+2y = 1\) is in the form \(Ax +By = C\). However, standard form requires that \(A ≥ 0\). We have \(A = −3\). To fix this, we multiply both sides by \(−1\).

\[\begin{aligned} -1[-3x+2y] &= -1[1] \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-2y &= -1 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

Thus, the equation of the line in standard form is \(3x−2y =−1\).

Note

If we fail to reduce the slope to lowest terms, then the equation of the line would be: \[y-2=\dfrac{6}{4}(x-1) \nonumber \]

Multiplying both sides by \(4\) would give us the result \[4y−8=6x−6 \nonumber \]or equivalently: \[−6x +4y =2 \nonumber \]

This doesn’t look like the same answer, but if we divide both sides by \(−2\), we do get the same result. \[3x−2y = −1 \nonumber \]

This shows the importance of requiring \(A ≥ 0\) and “reducing” the coefficients \(A\), \(B\), and \(C\). It allows us to compare our answer with our colleagues or the answers presented in this textbook.

Exercise \(\PageIndex{3}\)

Find the standard form of the equation of the line that passes through the points \((−2,4)\) and \((3,−3)\).

Answer

\(7x +5y =6\)

Intercepts

We’ve studied the \(y\)-intercept, the point where the graph crosses the \(y\)-axis, but equally important are the \(x\)-intercepts, the points where the graph crosses the \(x\)-axis.

Figure \(\PageIndex{5}\): Each \(x\)-intercept has a \(y\)-coordinate equal to zero.

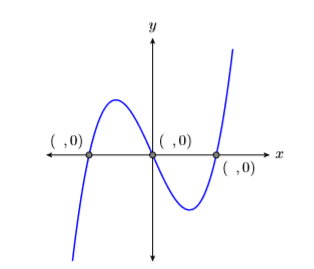
In Figure \(\PageIndex{5}\), the graph crosses the \(x\)-axis three times. Each of these crossing points is called an \(x\)-intercept. Note that each of these \(x\)-intercepts has a \(y\)-coordinate equal to zero. This leads to the following rule.

\(x\) Intercepts

To find the \(x\)-intercepts of the graph of an equation, substitute \(y = 0\) into the equation and solve for \(x\).

Figure \(\PageIndex{6}\): Each \(y\)-intercept has an \(x\)-coordinate equal to zero.

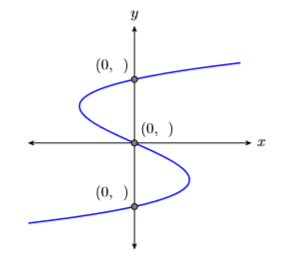
Similarly, the graph in Figure \(\PageIndex{6}\) crosses the \(y\)-axis three times. Each of these crossing points is called a \(y\)-intercept. Note that each of these \(y\)-intercepts has an \(x\)-coordinate equal to zero. This leads to the following rule.

\(y\) Intercepts

To find the \(y\)-intercepts of the graph of an equation, substitute \(x = 0\) into the equation and solve for \(y\).

Let’s put these rules for finding intercepts to work.

Example \(\PageIndex{4}\)

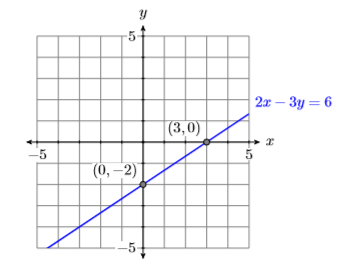
Find the \(x\)- and \(y\)-intercepts of the line having equation \(2x−3y = 6\). Plot the intercepts and draw the line.

Solution

We know that the graph of \(2x−3y = 6\) is a line. Furthermore, two points completely determine a line. This means that we need only plot the \(x\)- and \(y\)-intercepts, then draw a line through them.

To find the \(x\)-intercept of \(2x−3y = 6\), substitute \(0\) for \(y\) and solve for \(x\).

\[\begin{aligned} 2 x-3 y &=6 \\ 2 x-3(0) &=6 \\ 2 x &=6 \\ \dfrac{2 x}{2} &=\dfrac{6}{2} \\ x &=3 \end{aligned} \nonumber \]

Thus, the \(x\)-intercept of the line is \((3,0)\).

To find the \(y\)-intercept of \(2x−3y = 6\), substitute \(0\) for \(x\) and solve for \(y\).

\[\begin{aligned} 2 x-3 y &=6 \\ 2(0)-3 y &=6 \\-3 y &=6 \\ \frac{-3 y}{-3} &=\frac{6}{-3} \\ y &=-2 \end{aligned} \nonumber \]

Thus, the \(y\)-intercept of the line is \((0,−2)\).

Plot the \(x\)-intercept \((3,0)\) and the \(y\)-intercept \((0,−2)\) and draw a line through them (see Figure \(\PageIndex{7}\)).

Figure \(\PageIndex{7}\): The graph of \(2x−3y = 6\) has intercepts \((3,0)\) and \((0,−2)\).

Exercise \(\PageIndex{4}\)

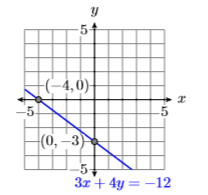
Find the \(x\)- and \(y\)-intercepts of the line having equation \(3x +4y = −12\). Plot the intercepts and draw the line.

Answer

\(x\)-intercept: \((−4,0)\)

\(y\)-intercept: \((0,−3)\)

Example \(\PageIndex{5}\)

Sketch the line \(4x +3 y = 12\), then sketch the line through the point \((−2,−2)\) that is perpendicular to the line \(4x +3 y = 12\). Find the equation of this perpendicular line.

Solution

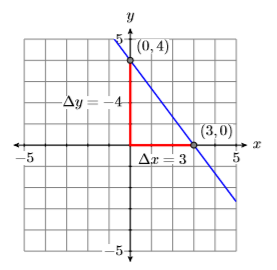
Let’s first find the \(x\)- and \(y\)-intercepts of the line \(4x +3y = 12\).

To find the \(x\)-intercept of the line \(4x+3y = 12\), substitute \(0\) for \(y\) and solve for \(x\).

\[\begin{aligned} 4 x+3 y &=12 \\ 4 x+3(0) &=12 \\ 4 x &=12 \\ \dfrac{4 x}{4} &=\dfrac{12}{4} \\ x &=3 \end{aligned} \nonumber \]

Thus, the \(x\)-intercept of the line is \((3,0)\).

To find the \(y\)-intercept of the line \(4x+3y = 12\), substitute \(0\) for \(x\) and solve for \(y\).

\[\begin{aligned} 4 x+3 y &=12 \\ 4(0)+3 y &=12 \\ 3 y &=12 \\ \dfrac{3 y}{3} &=\dfrac{12}{3} \\ y &=4 \end{aligned} \nonumber \]

Thus, the \(y\)-intercept of the line is \((0,4)\).

Plot the intercepts and draw a line through them. Note that it is clear from the graph that the slope of the line \(3x +4y = 12\) is \(−4/3\) (see Figure \(\PageIndex{8}\)).

Figure \(\PageIndex{8}\): The graph of \(4x+3y = 12\) has intercepts \((3,0)\) and \((0,4)\) and slope \(−4/3\).

You could also solve for \(y\) to put \(3x +4 y = 12\) in slope intercept form in order to determine the slope.

Because the slope of \(3x+4y = 12\) is \(−4/3\), the slope of a line perpendicular to \(3x +4y = 12\) will be the negative reciprocal of \(−4/3\), namely \(3/4\). Our perpendicular line has to pass through the point \((−2,−2)\). Start at \((−2,−2)\), move \(3\) units upward, then \(4\) units to the right, then draw the line. It should appear to be perpendicular to the line \(3x +4y = 12\) (see Figure \(\PageIndex{9}\)).

Figure \(\PageIndex{9}\): The slope of the perpendicular line is the negative reciprocal of \(−4/3\), namely \(3/4\).

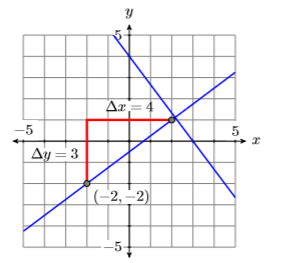
Finally, use the point-slope form, \(m =3 /4\), and \(\left(x_{0}, y_{0}\right)=(-2,-2)\) to determine the equation of the perpendicular line.

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-(-2) &= \dfrac{3}{4}(x-(-2)) \quad \color{Red} \text { Substitute: } 3 / 4 \text { for } m,-2 \text { for } x_{0} \text { and }-2 \text { for } y_{0} \\ y+2 &= \dfrac{3}{4}(x+2) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Let’s place our answer in standard form. Clear the fractions.

\[\begin{aligned} y+2 &= \dfrac{3}{4} x+\dfrac{6}{4} \quad \color{Red} \text { Distribute } 3 / 4 \\ 4[y+2] &= 4\left[\dfrac{3}{4} x+\dfrac{6}{4}\right] \quad \color{Red} \text { Multiply both sides by } 4 \\ 4y+4[2] &= 4\left[\dfrac{3}{4} x\right]+4\left[\dfrac{6}{4}\right] \quad \color{Red} \text { Distribute the } 4 \\ 4y+8 &= 3x+6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Rearrange the terms to put them in the order \(Ax + By = C\).

\[\begin{aligned} 4y+8-3x &= 3x+6-3x \quad \color{Red} \text { Subtract } 3x \text { from both sides. } \\ -3x+4y+8 &= 6 \quad \color{Red} \text { Simplify. Rearrange on the left. } \\ -3x+4y+8-8 &= 6-8 \quad \color{Red} \text { Subtract } 8 \text { from both sides. } \\ -3x+4y &= -2 \quad \color{Red} \text { Simplify. } \\ -1(-3x+4y) &= -1(-2) \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-4y &= 2 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

Hence, the equation of the perpendicular line is \(3x−4y = 2\).

Exercise \(\PageIndex{5}\)

Find the equation of the line that passes through the point \((3,2)\) and is perpendicular to the line \(6x−5y = 15\).

Answer

\(5x +6y = 27\)

Horizontal and Vertical Lines

Here we keep an earlier promise to address what happens to the standard form \(Ax + By = C\) when either \(A = 0\) or \(B = 0\). For example, the form \(3x = 6\), when compared with the standard form \(Ax + By = C\), has \(B = 0\). Similarly, the form \(2y = −12\), when compared with the standard form \(Ax + By = C\), has \(A = 0\). Of course, \(3 x = 6\) can be simplified to \(x = 2\) and \(2 y = −12\) can be simplified to \(y = −6\). Thus, if either \(A = 0\) or \(B = 0\), the standard form \(\)Ax + By = C takes the form \(x = a\) and \(y = b\), respectively.

As we will see in the next example, the form \(x = a\) produces a vertical line, while the form \(y = b\) produces a horizontal line.

Example \(\PageIndex{6}\)

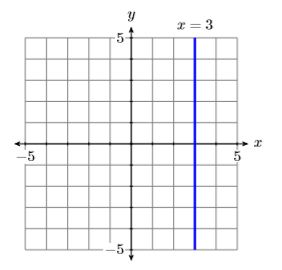
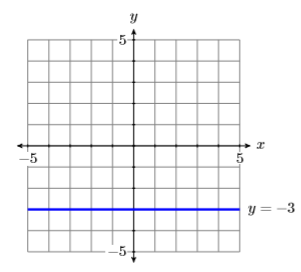
Sketch the graphs of \(x = 3\) and \(y = −3\).

Solution

To sketch the graph of \(x = 3\), recall that the graph of an equation is the set of all points that satisfy the equation. Hence, to draw the graph of \(x = 3\), we must plot all of the points that satisfy the equation \(x = 3\); that is, we must plot all of the points that have an \(x\)-coordinate equal to \(3\). The result is shown in Figure \(\PageIndex{10}\).

Figure \(\PageIndex{10}\): The graph of \(x = 3\) is a vertical line.

Secondly, to sketch the graph of \(y = −3\), we plot all points having a \(y\)-coordinate equal to \(−3\). The result is shown in Figure \(\PageIndex{11}\).

Figure \(\PageIndex{11}\): The graph of \(y =−3\) is a horizontal line.

Things to note:

A couple of comments are in order regarding the lines in Figures \(\PageIndex{10}\) and \(\PageIndex{11}\).

1. The graph of \(x = 3\) in Figure \(\PageIndex{10}\), being a vertical line, has undefined slope. Therefore, we cannot use either of the formulae \(y = mx + b\) or \(y−y_0 = m(x−x_0)\) to obtain the equation of the line. The only way we can obtain the equation is to note that the line is the set of all points \((x,y)\) whose \(x\)-coordinate equals \(3\).
2. However, the graph of \(y = −3\), being a horizontal line, has slope zero, so we can use the slope-intercept form to find the equation of the line. Note that the \(y\)-intercept of this graph is \((0,−3)\). If we substitute these numbers into \(y = mx + b\), we get:\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= 0x+(-3) \quad \color{Red} \text { Substitute: } 0 \text { for } m,-3 \text { for } b \\ y &= -3 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

However, it is far easier to just look at the line in Figures \(\PageIndex{11}\) and note that it is the collection of all points \((x,y)\) with \(y = 3\).

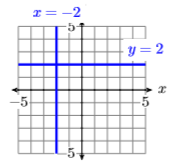
Exercise \(\PageIndex{6}\)

Sketch the graphs of \(x = −2\) and \(y = 2\).

Answer