4.4: Applications of Linear Systems

Last updated
Save as PDF

Page ID: 19873

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In this section we create and solve applications that lead to systems of linear equations. As we create and solve our models, we’ll follow the Requirements for Word Problem Solutions from Chapter 2, Section 5. However, instead of setting up a single equation, we set up a system of equations for each application.

Example $\PageIndex{1}$

In geometry, two angles that sum to $90^{\circ}$ are called complementary angles. If the second of two complementary angles is $30^{\circ}$ larger than twice the ﬁrst angle, ﬁnd the degree measure of both angles.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Our variable dictionary will take the form of a diagram, naming the two complementary angles $\alpha$ and $β$.

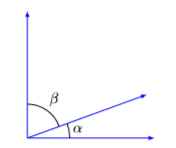
$fig 4.4.a.png$

Set up a Systems of Equations. The “second angle is $30$ degrees larger than twice the ﬁrst angle” becomes \[\beta=30+2 \alpha \label{Eq4.4.1}\]Secondly, the angles are complementary, meaning that the sum of the angles is $90^{\circ}$.\[\alpha+\beta=90 \label{Eq4.4.2}\]Thus, we have a system of two equations in two unknowns $\alpha$ and $β$.
Solve the System. As Equation \ref{Eq4.4.1} is already solved for $β$, let use the substitution method and substitute $30 + 2α$ for $β$ in Equation \ref{Eq4.4.2}.\[\begin{aligned} \alpha+\beta &= 90 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.2} \\ \alpha+(30+2 \alpha) &= 90 \quad \color {Red} \text { Substitute } 30+2 \alpha \text { for } \beta \\ 3 \alpha+30 &= 90 \quad \color {Red} \text { Combine like terms. } \\ 3 \alpha &= 60 \quad \color {Red} \text { Subtract } 30 \text { from both sides. } \\ \alpha &= 20 \quad \color {Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]
Answer the Question. The ﬁrst angle is $α = 20$ degrees. The second angle is:\[\begin{aligned} \beta &= 30+2 \alpha \quad {\color {Red} \text { Equation }}\ref{Eq4.4.1} \\ \beta &= 30+2(20) \quad \color {Red} \text { Substitute } 20 \text { for } \alpha \\ \beta &=70 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Look Back. Certainly $70^{\circ}$ is $30^{\circ}$ larger than twice $20^{\circ}$. Also, note that $20^{\circ}+70^{\circ}=90^{\circ}$, so the angles are complementary. We have the correct solution.

Exercise $\PageIndex{1}$

If the second of two complementary angles is $6^{\circ}$ larger than $3$ times the ﬁrst angle, ﬁnd the degree measure of both angles.

Answer: $21$ and $69$

Example $\PageIndex{2}$

The perimeter of a rectangle is $280$ feet. The length of the rectangle is $10$ feet less than twice the width. Find the width and length of the rectangle.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Our variable dictionary will take the form of a diagram, naming the width and length $W$ and $L$, respectively.

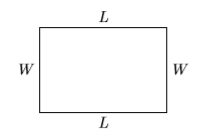
$fig 4.4.b.png$

Set up a System of Equations. The perimeter is found by summing the four sides of the rectangle.\[\begin{array}{l}{P=L+W+L+W} \\ {P=2 L+2 W}\end{array} \nonumber\]We’re told the perimeter is $280$ feet, so we can substitute $280$ for $P$ in the last equation.\[280=2 L+2 W \nonumber \]We can simplify this equation by dividing both sides by $2$, giving the following result: \[L+W=140 \nonumber \]Secondly, we’re told that the “length is $10$ feet less than twice the width.” This translates to: \[L=2 W-10 \nonumber \]Thus, the system we need to solve is: \[L+W=140 \label{Eq4.4.3} \]\[L=2 W-10 \label{Eq4.4.4} \]
Solve the System. As Equation \ref{Eq4.4.4} is already solved for $L$, let use the substitution method and substitute $2W −10$ for $L$ in Equation \ref{Eq4.4.3}.\[\begin{aligned} W+L &= 140 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.3} \\ W+(2 W-10) &= 140 \quad \color {Red} \text { Substitute } 2 W-10 \text { for } L \\ 3 W-10 &= 140 \quad \color {Red} \text { Combine like terms. } \\ 3 W &= 150 \quad \color {Red} \text { Add } 10 \text { to both sides. } \\ W &= 50 \quad \color {Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]
Answer the Question. The width is $W = 50$ feet. The length is: \[\begin{aligned} L &= 2W-10 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.4} \\ L &= 2(50)-10 \quad \color {Red} \text { Substitute } 50 \text { for } W. \\ L &= 90 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]Thus, the length is $L = 90$ feet.
Look Back. Perhaps a picture, labeled with our answers might best demonstrate that we have the correct solution. Remember, we found that the width was $50$ feet and the length was $90$ feet.

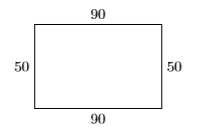
$fig 4.4.c.png$

Note that the perimeter is $P = 90 + 50 + 90 + 50 = 280$ feet. Secondly, note that the length $90$ feet is $10$ feet less than twice the width. So we have the correct solution.

Exercise $\PageIndex{2}$

The perimeter of a rectangle is $368$ meters. The length of the rectangle is $34$ meters more than twice the width. Find the width and length of the rectangle.

Answer: length $=134$, width $=50$

Example $\PageIndex{3}$

Pascal has $\$3.25$ in change in his pocket, all in dimes and quarters. He has $22$ coins in all. How many dimes does he have?

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $D$ represent the number of dimes and let $Q$ represent the number of quarters.

Set up a System of Equations. Using a table to summarize information is a good strategy. In the ﬁrst column, we list the type of coin. The second column gives the number of each type of coin, and the third column contains the value (in cents) of the number of coins in Pascal’s pocket.

	Number of Coins	Value (in cents)
Dimes	$D$	$10D$
Quarters	$Q$	$25Q$
Totals	$22$	$325$

Note that $D$ times, valued at $10$ cents apiece, are worth $10D$ cents. Similarly, $Q$ quarters, valued at $25$ cents apiece, are worth $25Q$ cents. Note also how we’ve change $\$3.25$ to $325$ cents. The second column of the table gives us our ﬁrst equation.\[D+Q=22 \label{Eq4.4.5}\]The third column of the table gives us our second equation.\[10 D+25 Q=325 \label{Eq4.4.6}\]

Solve the System. Because equations \ref{Eq4.4.5} and \ref{Eq4.4.6} are both in standard form $Ax + By = C$, we’ll use the elimination method to ﬁnd a solution. Because the question asks us to ﬁnd the number of dimes in Pascal’s pocket, we’ll focus on eliminating the $Q$-terms and keeping the $D$-terms.\[\begin{aligned} -25 D-25 Q &=-550 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.5} \color {Red} \text { by } -25\\ 10 D+25 Q &=325 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.6}\\ \hline-15 D\quad\qquad &=-225 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Dividing both sides of the last equation by $−15$ gives us $D = 15$.
Answer the Question. The previous solution tells us that Pascal has $15$ dimes in his pocket.

Look Back. Again, summarizing results in a table might help us see if we have the correct solution. First, because we’re told that Pascal has $22$ coins in all, and we found that he had $15$ dimes, this means that he must have $7$ quarters.

	Number of Coins	Value (in cents)
Dimes	$15$	$150$
Quarters	$7$	$175$
Totals	$22$	$325$

Fifteen dimes are worth $150$ cents, and $7$ quarters are worth $175$ cents. That’s a total of $22$ coins and $325$ cents, or $\$3.25$. Thus we have the correct solution.

Exercise $\PageIndex{3}$

Eloise has $\$7.10$ in change in her pocket, all in nickels and quarters. she has $46$ coins in all. How many quarters does she have?

Answer: $24$

Example $\PageIndex{4}$

Rosa inherits $\$10,000$ and decides to invest the money in two accounts, one portion in a certiﬁcate of deposit that pays $4\%$ interest per year, and the rest in a mutual fund that pays $5\%$ per year. At the end of the ﬁrst year, Rosa’s investments earn a total of $\$420$ in interest. Find the amount invested in each account.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $C$ represent the amount invested in the certiﬁcate of deposit and $M$ represent the amount invested in the mutual fund.

Set up a System of Equations. We’ll again use a table to summarize information.

	Rate	Amount invested	Interest
Certificate of Deposit	$4\%$	$C$	$0.04C$
Mutual Fund	$5\%$	$M$	$0.05M$
Totals		$10,000$	$420$

At $4\%$, the interest earned on a $C$ dollars investment is found by taking $4\%$ of $C$ (i.e., $0.04C$). Similarly, the interest earned on the mutual fund is $0.05M$. The third column of the table gives us our ﬁrst equation. The total investment is $\$10,000$.\[C+M=10000 \nonumber \]The fourth column of the table gives us our second equation. The total interest earned is the sum of the interest earned in each account.\[0.04 C+0.05 M=420 \nonumber \]Let’s clear the decimals from the last equation by multiplying both sides of the equation by $100$.\[4 C+5 M=42000 \nonumber \]Thus, the system we need to solve is:\[C+M=10000 \label{Eq4.4.7}\]\[4 C+5 M=42000 \label{Eq4.4.8}\]

Solve the System. Because equations \ref{Eq4.4.7} and \ref{Eq4.4.8} are both in standard form $Ax + By = C$, we’ll use the elimination method to ﬁnd a solution. We’ll focus on eliminating the $C$-terms.\[\begin{aligned} -4C-4M &=-40000 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.7} \color {Red} \text { by } -4\\ 4C+5M &=\;\;\;42000 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.8}\\ \hline-15 M &=\;\quad2000 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Thus, the amount invested in the mutual fund in $M = \$2 ,000$.
Answer the Question. The question asks us to ﬁnd the amount invested in each account. So, substitute $M = 2000$ in Equation \ref{Eq4.4.7} and solve for $C$.\[\begin{aligned} C+M &=10000 \quad {\color {Red} \text {Equation }} \ref{Eq4.4.7}\\ C+2000 &=10000 \quad \color {Red} \text { Substitute 2000 for M }\\ C &=\;\;8000 \quad \color {Red} \text {Subtract 2000 from both sides.} \end{aligned} \nonumber \]Thus $C = \$8 ,000$ was invested in the certiﬁcate of deposit.

Look Back. First, note that the investments in the certiﬁcate of deposit and the mutual fund, $\$8,000$ and $\$2,000$ respectively, total $\$10,000$. Let’s calculate the interest on each investment: $4\%$ of $\$8,000$ is $\$320$ and $5\%$ of $\$2,000$ is $\$100$.

	Rate	Amount invested	Interest
Certificate of Deposit	$4\%$	$8,000$	$320$
Mutual Fund	$5\%$	$2,000$	$100$
Totals		$10,000$	$420$

Note that the total interest is $\$420$, as required in the problem statement. Thus, our solution is correct.

Exercise $\PageIndex{4}$

Eileen inherits $\$40,000$ and decides to invest the money in two accounts, part in a certiﬁcate of deposit that pays $3\%$ interest per year, and the rest in a mutual fund that pays $6\%$ per year. At the end of the ﬁrst year, her investments earn a total of $\$2,010$ in interest. Find the amount invested in each account.

Answer: $\$13,000$ in the certiﬁcate of deposit, $\$27,000$ in the mutual fund.

Example $\PageIndex{5}$

Peanuts retail at $\$0.50$ per pound and cashews cost $\$1.25$ per pound. If you were a shop owner, how many pounds of peanuts and cashews should you mix to make $50$ pounds of a peanut-cashew mixture costing $\$0.95$ per pound?

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a Variable Dictionary. Let $P$ be the number of pounds of peanuts used and let $C$ be the number of pounds of cashews used.

Set up a System of Equations. We’ll again use a table to summarize information.

	Cost per pound	Amount (pounds)	Cost
Peanuts	$\$0.50$	$P$	$0.50P$
Cashews	$\$1.25$	$C$	$1.25C$
Totals	$\$0.95$	$50$	$0.95(50)=47.50$

At $\$0.50$ per pound, $P$ pounds of peanuts cost $0.50P$. At $\$1.25$ per pound, $C$ pounds of cashews cost $1.25C$. Finally, at $\$0.95$ per pound, $50$ pounds of a mixture of peanuts and cashews will cost $0.95(50)$, or $\$47.50$. The third column of the table gives us our ﬁrst equation. The total number of pounds of mixture is given by the following equation:\[P+C=50 \nonumber \]The fourth column of the table gives us our second equation. The total cost is the sum of the costs for purchasing the peanuts and cashews.\[0.50 P+1.25 C=47.50 \nonumber \]Let’s clear the decimals from the last equation by multiplying both sides of the equation by $100$.\[50 P+125 C=4750 \nonumber \]Thus, the system we need to solve is:\[P+C=50 \label{Eq4.4.9}\]\[50 P+125 C=4750 \label{Eq4.4.10}\]

Solve the System. Because equations \ref{Eq4.4.9} and \ref{Eq4.4.10} are both in standard form $Ax + By = C$, we’ll use the elimination method to ﬁnd a solution. We’ll focus on eliminating the $P$-terms.\[\begin{aligned} -50P-50C &=-2500 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.9} \color {Red} \text { by } -50\\ 50P+125C &=\;\;\;4750 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.10}\\ \hline 75C &=\quad2250 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Divide both sides by $75$ to get $C = 30$ pounds of cashews are in the mix.
Answer the Question. The question asks for both amounts, peanuts and cashews. Substitute $C = 30$ in Equation \ref{Eq4.4.9} to determine $P$.\[\begin{aligned} P+C &=50 \quad {\color {Red} \text {Equation }} \ref{Eq4.4.9}\\ C+30 &=50 \quad \color {Red} \text { Substitute 30 for C }\\ P &=20 \quad \color {Red} \text {Subtract 30 from both sides.} \end{aligned} \nonumber\]Thus, there are $P = 20$ pounds of peanuts in the mix.

Look Back. First, note that the amount of peanuts and cashews in the mix is $20$ and $30$ pounds respectively, so the total mixture weighs $50$ pounds as required. Let’s calculate the costs: for the peanuts, $0.50(20)$, or $\$10$, for the cashews, $1.25(30) = 37.50$.

	Cost per pound	Amount (pounds)	Cost
Peanuts	$\$0.50$	$20$	$\$10.00$
Cashews	$\$1.25$	$30$	$\$37.50$
Totals	$\$0.95$	$50$	$\$47.50$

Note that the total cost is $\$47.50$, as required in the problem statement. Thus, our solution is correct.

Exercise $\PageIndex{5}$

A store sells peanuts for $\$4.00$ per pound and pecans for $\$7.00$ per pound. How many pounds of peanuts and how many pounds of pecans should you mix to make a $25$-lb mixture costing $\$5.80$ per pound?

Answer: $10$ pounds of peanuts, $15$ pounds of pecans

	Number of Coins	Value (in cents)
Dimes	\(D\)	\(10D\)
Quarters	\(Q\)	\(25Q\)
Totals	\(22\)	\(325\)

	Number of Coins	Value (in cents)
Dimes	\(15\)	\(150\)
Quarters	\(7\)	\(175\)
Totals	\(22\)	\(325\)

	Rate	Amount invested	Interest
Certificate of Deposit	\(4\%\)	\(C\)	\(0.04C\)
Mutual Fund	\(5\%\)	\(M\)	\(0.05M\)
Totals		\(10,000\)	\(420\)

	Rate	Amount invested	Interest
Certificate of Deposit	\(4\%\)	\(8,000\)	\(320\)
Mutual Fund	\(5\%\)	\(2,000\)	\(100\)
Totals		\(10,000\)	\(420\)

	Cost per pound	Amount (pounds)	Cost
Peanuts	\(\$0.50\)	\(P\)	\(0.50P\)
Cashews	\(\$1.25\)	\(C\)	\(1.25C\)
Totals	\(\$0.95\)	\(50\)	\(0.95(50)=47.50\)

	Cost per pound	Amount (pounds)	Cost
Peanuts	\(\$0.50\)	\(20\)	\(\$10.00\)
Cashews	\(\$1.25\)	\(30\)	\(\$37.50\)
Totals	\(\$0.95\)	\(50\)	\(\$47.50\)