6.3: Factoring ax² + bx + c when a =1
- Page ID
- 19886
In this section we concentrate on learning how to factor trinomials having the form \(ax^2 +bx+c\) when \(a = 1\). The first task is to make sure that everyone can properly identify the coefficients \(a\), \(b\), and \(c\).
Example \(\PageIndex{1}\)
Compare \(x^2−8x−9\) with the form \(ax^2 +bx+c\) and identify the coefficients \(a\), \(b\), and \(c\).
Solution
Align the trinomial \(x^2−8x−9\) with the standard form \(ax^2 +bx+c\), then compare coefficients. Note that the understood coefficient of \(x^2\) is \(1\).
\[\begin{array}{l}{a x^{2}+b x+c} \\ {{\color {Red}1} x^{2}-8 x-9}\end{array} \nonumber \]
We see that \(a = 1\), \(b = −8\), and \(c = −9\). Because the leading coefficient is \(1\), this is the type of trinomial that we will learn how to factor in this section.
Exercise \(\PageIndex{1}\)
Compare \(2x^2 +5x−3\) with the form \(ax^2 + bx + c\) and identify the coefficients \(a\), \(b\), and \(c\).
- Answer
-
\(a = 2\), \(b = 5\), \(c =−3\)
Example \(\PageIndex{2}\)
Compare \(−40 + 6x^2 − x\) with the form \(ax^2 + bx + c\) and identify the coefficients \(a\), \(b\), and \(c\).
Solution
First, arrange \(−40+ 6x^2 −x\) in descending powers of \(x\), then align it with the standard form \(ax^2 +bx+c\) and compare coefficients. Note that the understood coefficient of \(x\) is \(−1\).
\[\begin{array}{l}{a x^{2}+b x+c} \\ {6 x^{2}-{\color {Red} 1} x-40}\end{array} \nonumber \]
We see that \(a = 6\), \(b = −1\), and \(c = −40\). Because the leading coefficient is \(6\), we will have to wait until we learn about factoring \(ax^2 + bx + c\) when \(a \neq 1\) in section 6.4 before learning how to factor this trinomial.
Exercise \(\PageIndex{2}\)
Compare \(3x +9−7x^2\) with the form \(ax^2 + bx + c\) and identify the coefficients \(a\), \(b\), and \(c\).
- Answer
-
\(a = −7\), \(b = 3\), \(c =9\)
In this section, the leading coefficient must equal \(1\). Our work in this section will focus only on trinomials of the form \(x^2 + bx + c\), that is, the form \(ax^2 + bx + c\) where \(a = 1\).
The \(ac\)-Method
We are now going to introduce a technique called the \(ac\)-method (or \(ac\)-test) for factoring trinomials of the form \(ax^2 +bx+c\) when \(a = 1\). In the upcoming section 6.4 about factoring \(ax^2 + bx + c\) when \(a \neq 1\), we will see that this method can also be employed when \(a \neq 1\), with one minor exception. But for the remainder of this section, we focus strictly on trinomials whose leading coefficient is \(1\).
Let’s begin by finding the following product:
\[\begin{aligned}(x+12)(x-4) &=x(x-4)+12(x-4) \quad \color {Red} \text { Apply the distributive property. } \\ &=x^{2}-4 x+12 x-48 \quad \color {Red } \text { Distribute again. } \\ &=x^{2}+8 x-48 \quad \color {Red} \text { Simplify. }\end{aligned} \nonumber \]
Now, can we reverse the process? That is, can we start with \(x^2 +8x−48\) and place it in its original factored form \((x + 12)(x−4)\)? The answer is yes, if we apply the following procedure.
The \(ac\)-method
Compare the given polynomial with the standard form \(ax^2 + bx + c\), determine the coefficients \(a\), \(b\), and \(c\), then proceed as follows:
- Multiply the coefficients \(a\) and \(c\) and determine their product \(ac\). List all the integer pairs whose product equals \(ac\).
- Circle the pair in the list produced in step 1 whose sum equals \(b\), the coefficient of the middle term of \(ax^2 + bx + c\).
- Replace the middle term \(bx\) with a sum of like terms using the circled pair from step 2.
- Factor by grouping.
- Check the result using the FOIL shortcut.
Let’s follow the steps of the \(ac\)-method to factor \(x^2 +8x−48\).
Example \(\PageIndex{3}\)
Factor: \(x^2 +8x−48\).
Solution
Compare \(x^2+8x−48\) with \(ax^2+bx+c\) and identify \(a = 1\), \(b = 8\), and \(c = −48\). Note that the leading coefficient is \(a = 1\). Calculate \(ac\). Note that \(ac = (1)(−48)\), so \(ac =−48\). List all integer pairs whose product is \(ac = −48\).
\[\begin{array}{ll}{1,-48} & {-1,48} \\ {2,-24} & {-2,24} \\ {3,-16} & {-3,16} \\ {4,-12} & { -4,12} \\ {6,-8} & {-6,8}\end{array} \nonumber \]
Circle the ordered pair whose sum is \(b = 8\).
\[\begin{array}{ll}{1,-48} & {-1,48} \\ {2,-24} & {-2,24} \\ {3,-16} & {-3,16} \\ {4,-12} & {\color {Red}-4,12} \\ {6,-8} & {-6,8}\end{array} \nonumber \]
Replace the middle term \(8x\) with a sum of like terms using the circled pair whose sum is \(8\).
\[x^2{\color {Red}+8x}-48 = x^2{\color {Red}-4x + 12x}-48 \nonumber \]
Factor by grouping.
\[\begin{aligned} x^{2}+8 x-48 &=x(x-4)+12(x-4) \\ &=(x+12)(x-4) \end{aligned} \nonumber \]
Use the FOIL shortcut to mentally check your answer. To determine the product \((x + 12)(x−4)\), use these steps:
- Multiply the terms in the “First” positions: \(x^2\).
- Multiply the terms in the “Outer” and “Inner” positions and combine the results mentally: \(−4x + 12x =8x\).
- Multiply the terms in the “Last” positions: \(−48\).
That is:
\[(x+12)(x-4) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&-&4x&+&12x&-&48 \end{array} \nonumber \]
Combining like terms, \((x + 12)(x−4) = x^2 +8x−48\), which is the original trinomial, so our solution checks. Note that if you combine the “Outer” and “Inner” products mentally, the check goes even faster.
Exercise \(\PageIndex{3}\)
Factor: \(x^2 + 11x + 28\)
- Answer
-
\((x+4)(x+7)\)
Some readers might ask “Is it a coincidence that the circled pair \(\color {Red} −4,12\) seemed to ‘drop in place’ in the resulting factorization \((x+12)(x−4)\)?” Before we answer that question, let’s try another example.
Example \(\PageIndex{4}\)
Factor: \(x^2 −9x−36\).
Solution
Compare \(x^2−9x−36\) with \(ax^2+bx+c\) and note that \(a = 1\), \(b = −9\), and \(c =−36\). Calculate \(ac = (1)(−36)\), so \(ac = −36\).
At this point, some readers might ask “What if I start listing the ordered pairs and I see the pair I need? Do I need to continue listing the remaining pairs?
The answer is “No.” In this case, we start listing the integer pairs whose product is \(ac = −36\), but are mindful that we need an integer pair whose sum is \(b =−9\). The integer pair \(3\) and \(−12\) has a product equaling \(ac =−36\) and a sum equaling \(b =−9\).
\[\begin{array}{r}{1,-36} \\ {2,-18} \\ {\color {Red}3,-12} \end{array} \nonumber \]
Note how we ceased listing ordered pairs the moment we found the pair we needed. Next, replace the middle term \(−9x\) with a sum of like terms using the circled pair.
\[x^2{\color {Red}-9x}-36 = x^2{\color {Red}+3x-12x}-36 \nonumber \]
Factor by grouping.
\[\begin{aligned} x^{2}{\color {Red}-9 x}-36 &=x(x+3)-12(x+3) \\ &=(x-12)(x+3) \end{aligned} \nonumber \]
Use the FOIL shortcut to check your answer.
\[(x+3)(x-12) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&-&12x&+&3x&-&36 \end{array} \nonumber\]
Combining like terms, \((x + 3)(x−12) = x^2 −9x−36\), the original trinomial. Our solution checks.
Exercise \(\PageIndex{4}\)
Factor: \(x2 + 10x−24\).
- Answer
-
\(( x + 12)(x−2)\)
Speeding Things Up a Bit
Readers might again ask “Is it a coincidence that the circled pair \(\color {Red} 3,−12\) seemed to ‘drop in place’ in the resulting factoriztion \((x−12)(x + 3)\)?” The answer is “No,” it is not a coincidence. Provided the leading coefficient of the trinomial \(ax^2 +bx+c\) is \(a = 1\), you can always “drop in place” the circled pair in order to arrive at the final factorization, skipping the factoring by grouping.
Some readers might also be asking “Do I really have to list any of those ordered pairs if I already recognize the pair I need?” The answer is “No!” If you see the pair you need, drop it in place.
Example \(\PageIndex{5}\)
Factor: \(x^2 −5x−24\).
Solution
Compare \(x^2−5x−24\) with \(ax^2+bx+c\) and note that \(a = 1\), \(b =−5\), and \(c =−24\). Calculate \(ac = (1)(−24)\), so \(ac = −24\). Now can you think of an integer pair whose product is \(ac = −24\) and whose sum is \(b = −5\)? For some, the required pair just pops into their head: \(−8\) and \(3\). The product of these two integers is \(−24\) and their sum is \(−5\).“Drop” this pair in place and you are done.
\[x^2 −5x−24 = (x−8)(x + 3) \nonumber \]
Use the FOIL shortcut to check your answer.
\[(x-8)(x+3) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&+&3x&-&8x&-&24 \end{array} \nonumber\]
Combining like terms, \((x−8)(x + 3) =x^2 −5x−24\), the original trinomial. Our solution checks.
Exercise \(\PageIndex{5}\)
Factor: \(x^2 −12x + 35\)
- Answer
-
\((x−7)(x−5)\)
The “Drop in Place” technique of Example \(\PageIndex{5}\) allows us to revise the \(ac\) method a bit.
Revised \(ac\)-method
Compare the given polynomial with the standard form \(ax^2 + bx + c\), determine the coefficients \(a\), \(b\), and \(c\), then determine a pair of integers whose product equals \(ac\) and whose sum equals \(b\). You then have two options:
- Write the middle term as a product of like terms using the ordered pair whose product is \(ac\) and whose sum is \(b\). Complete the factorization process by factoring by grouping.
- (Only works if \(a =1\).) Simply “drop in place” the ordered pair whose product is \(ac\) and whose sum is \(b\) to complete the factorization process. Note: We'll learn about factoring \(ax^2 + bx + c\) when \(a \neq 1\) in section 6.4 why this “drop in place” choice does not work when \(a \neq 1\)
Readers are strongly encouraged to check their factorization by determining the product using the FOIL method. If this produces the original trinomial, the factorization is correct.
Nonlinear Equations Revisited
The ability to factor trinomials of the form \(ax^2 +bx+c\), where \(a = 1\), increases the number of nonlinear equations we are now able to solve.
Example \(\PageIndex{6}\)
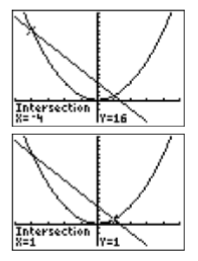
Solve the equation \(x^2 =2 x + 3\) both algebraically and graphically, then compare your answers.
Solution
Because there is a power of \(x\) larger than one, the equation is nonlinear. Make one side zero.
\[\begin{aligned} x^{2} &=2 x+3 \quad \color {Red} \text { Original equation. } \\ x^{2}-2 x &=3 \quad \color {Red} \text { Subtract } 2 x \text { from both sides. } \\ x^{2}-2 x-3 &=0 \quad \color {Red} \text { Subtract } 3 \text { from both sides. }\end{aligned} \nonumber \]
Compare \(x^2−2x−3\) with \(ax^2+bx+c\) and note that \(a = 1\), \(b =−2\) and \(c =−3\). We need an integer pair whose product is \(ac = −3\) and whose sum is \(b = −2\). The integer pair \(1\) and \(−3\) comes to mind. “Drop” these in place to factor.
\[(x + 1)(x-3) = 0 \quad \color {Red} \text {Factor.} \nonumber \]
We have a product that equals zero. Use the zero product property to complete the solution.
\[\begin{aligned} x+1 &=0 \\ x &=-1 \end{aligned} \nonumber \]
or
\[\begin{array}{r}{x-3=0} \\ {x=3}\end{array} \nonumber \]
Thus, the solutions of \(x^2 =2x + 3\) are \(x = −1\) and \(x = 3\).
Graphical solution:
Load each side of the equation \(x^2 =2 x + 3\) into the Y= menu of your graphing calculator, \(y = x^2\) in \(\mathbb {Y1}\), \(y =2x + 3\) in \(\mathbb {Y2}\) (see Figure \(\PageIndex{1}\)). Select 6:ZStandard from the ZOOM menu to produce the image at the right in Figure \(\PageIndex{1}\).
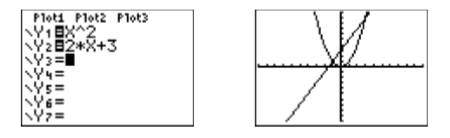
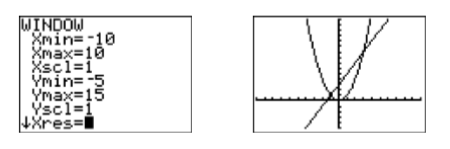
One of the intersection points is visible on the left, but the second point of intersection is very near the top of the screen at the right (see Figure \(\PageIndex{1}\)). Let’s extend the top of the screen a bit. Press the WINDOW button and make adjustments to \(\mathbb{Ymin}\) and \(\mathbb{Ymax}\) (see Figure \(\PageIndex{2}\)), then press the GRAPH button to adopt the changes.
Note that both points of intersection are now visible in the viewing window (see Figure \(\PageIndex{2}\)). To find the coordinates of the points of intersection, select 5:intersect from the CALC menu. Press the ENTER key to accept the “First curve,” press ENTER again to accept the “Second curve,” then press ENTER again to accept the current position of the cursor as your guess. The result is shown in the image on the left in Figure \(\PageIndex{3}\). Repeat the process to find the second point of intersection, only when it comes time to enter your “Guess,” use the right-arrow key to move the cursor closer to the second point of intersection than the first.
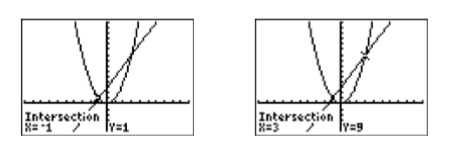
Reporting the solution on your homework:
Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
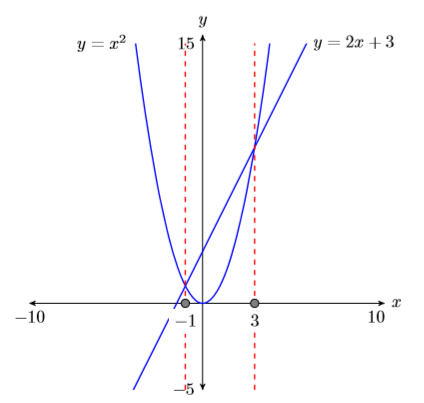
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{4}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{4}\)).
- Label each graph with its equation (see Figure \(\PageIndex{4}\)).
- Drop dashed vertical lines through each point of intersection. Shade and label the \(x\)-values of the points where the dashed vertical line crosses the \(x\)-axis. These are the solutions of the equation \(x^2 =2 x + 3\) (see Figure \(\PageIndex{4}\)).
Finally, note how the graphical solutions of \(x^2 =2 x + 3\), namely \(x = −1\) and \(x = 3\), match the solutions found using the algebraic method. This is solid evidence that both methods of solution are correct. However, it doesn’t hurt to check the final answers in the original equation, substituting \(−1\) for \(x\) and \(3\) for \(x\).
\[\begin{aligned} x^{2} &=2 x+3 \\(-1)^{2} &=2(-1)+3 \\ 1 &=-2+3 \end{aligned} \nonumber \]
and
\[\begin{aligned} x^{2} &=2 x+3 \\(3)^{2} &=2(3)+3 \\ 9 &=6+3 \end{aligned} \nonumber \]
Because the last two statements are true statements, the solutions \(x = −1\) and \(x = 3\) check in the original equation \(x^2 =2x + 3\).
Exercise \(\PageIndex{6}\)
Solve the equation \(x^2 = −3x + 4\) both algebraically and graphically, then compare your answers.
- Answer
-
\(-4\), \(1\)
Example \(\PageIndex{7}\)
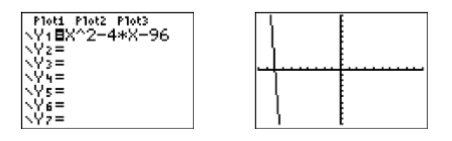
Solve the equation \(x^2 −4x−96 = 0\) both algebraically and graphically, then compare your answers.
Solution
Because there is a power of \(x\) larger than one, the equation \(x^2 − 4x−96 = 0\) is nonlinear. We already have one side zero, so we can proceed with the factoring. Begin listing integer pairs whose product is \(ac = −96\), mindful of the fact that we need a pair whose sum is \(b = −4\).
\[\begin{array}{l}{1,-96} \\ {2,-48} \\ {3,-32} \\ {4,-24} \\ {6,-16} \\ {\color {Red}8,-12} \\ \end{array} \nonumber \]
Note that we stopped the listing process as soon as we encountered a pair whose sum was \(b = −4\). “Drop” this pair in place to factor the trinomial.
\[\begin{aligned}x^{2}-4 x-96 &=0 \quad \color {Red} \text { Original equation. } \\ (x+8)(x-12) &=0 \quad \color {Red} \text { Factor. }\end{aligned} \nonumber \]
We have a product that equals zero. Use the zero product property to complete the solution.
\[\begin{aligned} x+8 &=0 \\ x &=-8 \end{aligned} \nonumber \]
or
\[\begin{aligned} x-12 &=0 \\ x &=12 \end{aligned} \nonumber \]
Thus, the solutions of \(x^2 −4x−96 = 0\) are \(x =−8\) and \(x = 12\).
Graphical solution:
Load the equation \(y = x^2 −4x−96\) in \(\mathbb{Y1}\) in the Y= menu of your graphing calculator (see Figure \(\PageIndex{5}\)). Select 6:ZStandard from the ZOOM menu to produce the image at the right in Figure \(\PageIndex{5}\).
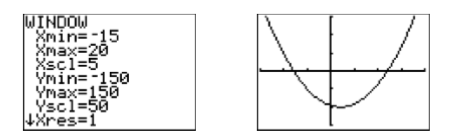
When the degree of a polynomial is two, we’re used to seeing some sort of parabola. In Figure \(\PageIndex{5}\), we saw the graph go down and off the screen, but we did not see it turn and come back up. Let’s adjust the WINDOW parameters so that the vertex (turning point) of the parabola and both \(x\)-intercepts are visible in the viewing window. After some experimentation, the settings shown in Figure \(\PageIndex{6}\) reveal the vertex and the \(x\)-intercepts. Press the GRAPH button to produce the image at the right in Figure \(\PageIndex{6}\).
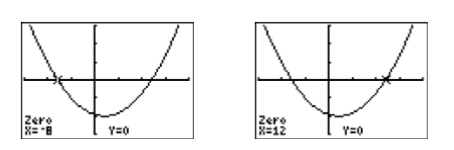
Note that both \(x\)-intercepts of the parabola are now visible in the viewing window (see Figure \(\PageIndex{6}\)). To find the coordinates of the \(x\)-intercepts, select 2:zero from the CALC menu. Use the left- and right-arrow keys to move the cursor to the left of the first \(x\)-intercept, then press ENTER to mark the “Left bound.” Next, move the cursor to the right of the first \(x\)-intercept, then press ENTER to mark the “Right bound.” Press ENTER to accept the current position of the cursor as your “Guess.” The result is shown in the image on the left in Figure \(\PageIndex{7}\). Repeat the process to find the coordinates of the second \(x\)-intercept. The result is show in the image on the right in Figure \(\PageIndex{7}\).
Reporting the solution on your homework: Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{8}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{8}\)).
- Label the graph with its equation (see Figure \(\PageIndex{8}\)).
- Drop dashed vertical lines through each \(x\)-intercept. Shade and label the \(x\)-values of the points where the dashed vertical line crosses the \(x\)-axis. These are the solutions of the equation \(x^2−4x−96 = 0\) (see Figure \(\PageIndex{8}\)).
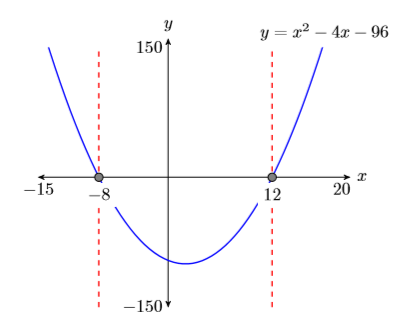
Finally, note how the graphical solutions of \(x^2 −4x−96 = 0\), namely \(x = −8\) and \(x = 12\), match the solutions found using the algebraic method. This is solid evidence that both methods of solution are correct. However, it doesn’t hurt to check the final answers in the original equation, substituting \(−8\) for \(x\) and \(12\) for \(x\).
\[\begin{array}{r}{x^{2}-4 x-96=0} \\ {(-8)^{2}-4(-8)-96=0} \\ {64+32-96=0}\end{array} \nonumber \]
and
\[\begin{aligned} x^{2}-4 x-96 &=0 \\(12)^{2}-4(12)-96 &=0 \\ 144-48-96 &=0 \end{aligned} \nonumber \]
Because the last two statements are true statements, the solutions \(x = −8\) and \(x = 12\) check in the original equation \(x^2 −4x−96−0\).
Exercise \(\PageIndex{7}\)
Solve the equation \(x^2 −21x + 90 = 0\) both algebraically and graphically, then compare your answers.
- Answer
-
\(6\), \(15\)



