6.4: Factoring ax² + bx + c when a≠1
- Page ID
- 19887
In this section we continue to factor trinomials of the form \(ax^2 + bx + c\). In the last section, all of our examples had \(a = 1\), and we were able to “Drop in place” our circled integer pair. However, in this section, \(a \neq 1\), and we’ll soon see that we will not be able to use the “Drop in place” technique. However, readers will be pleased to learn that the \(ac\)-method will still apply.
Example \(\PageIndex{1}\)
Factor: \(2x^2 −7x−15\).
Solution
We proceed as follows:
- Compare \(2x^2 −7x−15\) with \(ax^2 + bx + c\) and identify \(a = 2\), \(b = −7\), and \(c = −15\). Note that the leading coefficient is \(a = 2\), so this case is different from all of the cases discussed in Section 6.3.
- Calculate \(ac\). Note that \(ac = (2)(−15)\), so \(ac = −30\).
- List all integer pairs whose product is \(ac =−30\). \[\begin{array}{ll}{1,-30} & {-1,30} \\ {2,-15} & {-2,15} \\ {3,-10} & {-3,10} \\ {5,-6} & {-5,6}\end{array} \nonumber \]
- Circle the ordered pair whose sum is \(b =−7\).\[\begin{array}{cc}{1,-30} & {-1,30} \\ {2,-15} & {-2,15} \\ {\color {Red}3,-10} & {-3,10} \\ {5,-6} & {-5,6}\end{array} \nonumber \]
- Note that if we “drop in place” our circled ordered pair, \((x+3)(x-10) \neq 2x^2-7x-15\). Right off the bat, the product of the terms in the “First” position does not equal \(2x^2\). Instead, we break up the middle term of \(2x^2 −7x−15\) into a sum of like terms using our circled pair of integers \(3\) and \(−10\). \[2x^2{\color {Red}-7x}-15 = 2x^2{\color {Red}+3x-10x}-15 \nonumber \]Now we factor by grouping. Factor \(x\) out of the first two terms and \(−5\) out of the second two terms.\[= x(2x + 3)−5(2x + 3) \nonumber \]Now we can factor out (2x + 3).\[=(x−5)(2x + 3) \nonumber \]
- Use the FOIL shortcut to mentally check your answer. To multiply \((x−5)(2x + 3)\), use these steps:
- Multiply the terms in the “First” positions: \(2x^2\).
- Multiply the terms in the “Outer” and “Inner” positions and combine the results mentally: \(3x−10x = −7x\).
- Multiply the terms in the “Last” positions: \(−15\). That is:\[(x-5)(2x+3)=\begin{array}{ccccccc} \color {Red}F & & \color {Red}O & & \color {Red}I & & \color {Red}L \\ 2x^2&+&3x&-&10x&-&15 \end{array} \nonumber \]
Combining like terms, \((x − 5)(2x + 3) = 2x^2 − 7x − 15\), which is the original trinomial, so our solution checks. Note that if you combine the “Outer” and “Inner” products mentally, the check goes even faster.
Exercise \(\PageIndex{1}\)
Factor: \(3x^2 + 13x + 14\)
- Answer
-
\((x + 2)(3x + 7)\)
Speeding Things Up a Bit
Some readers might already be asking “Do I really have to list all of those ordered pairs if I already see the pair I need?” The answer is “No!” If you see the pair you need, use it to break up the middle term of the trinomial as a sum of like terms.
Example \(\PageIndex{2}\)
Factor: \(3x^2 −7x−6\).
Solution
Compare \(3x^2−7x−6\) with \(ax^2+bx+c\) and note that \(a = 3\), \(b =−7\), and \(c = −6\). Calculate \(ac = (3)(−6)\), so \(ac = −18\). Now can you think of an integer pair whose product is \(ac = −18\) and whose sum is \(b = −7\)? For some, the pair just pops into their head: \(2\) and \(−9\). Break up the middle term into a sum of like terms using the pair \(2\) and \(−9\).
\[\begin{align*} 3x^2{\color {Red}-7x}-6 &= 3x^2{\color {Red}+2x-9x}-6 \quad \color {Red} -7x=2x-9x\\ &= x(3x+2)-3(3x+2) \quad \color {Red} \text {Factor by grouping.}\\ &= (x-3)(3x+2) \quad \color {Red} \text {Factor out} (3x+2). \end{align*} \nonumber \]
Use the FOIL shortcut to check your answer.
\[(x-3)(3x+2)=\begin{array}{ccccccc} \color {Red}F & & \color {Red}O & & \color {Red}I & & \color {Red}L \\ 3x^2&+&2x&-&9x&-&6 \end{array} \nonumber \]
Combining like terms, \((x−3)(3x+2) = 3x^2−7x−6\), the original trinomial. Our solution checks. Note that if you combine the “Outer” and “Inner” products mentally, the check goes even faster.
Exercise \(\PageIndex{2}\)
Factor: \(2x^2 −9x + 10\)
- Answer
-
\((x−2)(2x−5)\)
On the other hand, some readers might be saying “Well, the needed ordered pair is not popping into my head. Do I have a way of cutting down the work?” The answer is “Yes!” As you are listing the ordered pairs whose product equals \(ac\), be mindful that you need the ordered pair whose sum is \(b\). If you stumble across the needed pair, stop the listing process and “drop” your ordered pair in place.
Example \(\PageIndex{3}\)
Factor: \(3x^2 −33x + 54\).
Solution
Compare \(3x^2 −33x + 54\) with \(ax^2 + bx + c\) and note that \(a = 3\), \(b = −33\), and \(c = 54\). Calculate \(ac = (3)(54)\), so \(ac = 162\). Ouch! That’s a big number! However, start listing the integer pairs whose product is \(ac = 162\), but be mindful that you need an integer pair whose sum is \(b = −33\).
\[\begin{array}{ll}{1,162} \\ {2,81} \\ {3,54} \\ {6,27} & {\color {Red}-6,-27}\end{array} \nonumber\]
As soon as we wrote down the pair \(6\) and \(27\), our mind said “the sum of \(6\) and \(7\) is \(33\).” However, we need the sum to equal \(b = −33\), so we boxed \(−6\) and \(−27\) instead. Next, we break up the middle term into a sum of like terms using our circled pair.
\[\begin{align*} 3x^2{\color {Red}-33x}-54 &= 3x^2{\color {Red}-6x-27x}-54 \quad \color {Red} -33x=-6x-27x\\ &= 3x(x-2)-27(x-2) \quad \color {Red} \text {Factor by grouping.}\\ &= (3x-27)(x-2) \quad \color {Red} \text {Factor out} (x-2). \end{align*} \nonumber\]
Oh-oh! Now we realize we can factor \(3\) out of each term in the first factor!
\[= 3(x−9)(x−2) \nonumber \]
We missed taking out the \(\mathrm {GCF}\)! Let’s try again, only this time let’s do what we are always supposed to do in the first step: Factor out the \(\mathrm {GCF}\).
\[3x^2 −33x + 54 = 3(x^2 −11x + 18) \nonumber \]
Comparing \(x^2 − 11x + 18\) with \(ax^2 + bx + c\), we see that \(a = 1\), \(b = −11\), and \(c = 18\). We need an integer pair whose product is \(ac = 18\) and whose sum is \(b = −11\). Note that these numbers are considerably smaller than the numbers we had to deal with when we forgot to first factor out the \(\mathrm {GCF}\). Because the numbers are smaller, the integer pair \(−9\) and \(−2\) easily comes to mind. Furthermore, because \(a = 1\), we can factor \(x^2 − 11x + 18\) by simply dropping the integer pair \(−9\) and \(−2\) in place.
\[3(x2 −11x + 18) = 3(x−9)(x−2) \nonumber \]
A far simpler solution!
Exercise \(\PageIndex{3}\)
Factor: \(5x^2 −35x−40\)
- Answer
-
\(5( x−8)(x + 1)\)
In Example \(\PageIndex{3}\), we saw how much more difficult we made the problem by forgetting to first factor out the greatest common factor (\(\mathrm {GCF}\)). Let’s try not to make that mistake again.
First rule of factoring
The first step in factoring any polynomial is to factor out the greatest common factor.
Example \(\PageIndex{4}\)
Factor: \(30x^3 −21x^2 −18x\).
Solution
Note that the \(\mathrm {GCF}\) of \(30x^3\), \(21x^2\), and \(18x\) is \(3x\). Factor out this \(\mathrm {GCF}\).
\[\begin{align*} 30x^3-21x^2-18x &= {\color{Red}3x}\cdot 10x^2-{\color{Red}3x}\cdot 7x -{\color{Red}3x}\cdot 6\\ &= {\color{Red}3x}(10x^2-7x-6) \end{align*} \nonumber \]
Next, compare \(10x^2 −7x−6\) with \(ax^2 + bx + c\) and note that \(a = 10\), \(b =−7\), and \(c = −6\). Start listing the integer pairs whose product is \(ac = −60\), but be mindful that you need an integer pair whose sum is \(b = −7\).
\[\begin{array}{ll}{1,-60} \\ {2,-30} \\ {3,-20} \\ {4,-15} \\ {\color {Red}5,-12}\end{array} \nonumber\]
Break up the middle term into a sum of like terms using our circled pair.
\[\begin{align*} 3x(10x^2-7x-6) &= 3x(10x^2+5x-12x-18) \quad \color {Red} -7x=5x-12x\\ &= 3x[5x(2x+1)-6(2x+1)] \quad \color {Red} \text {Factor by grouping.}\\ &= 3x(5x-6)(2x+1) \quad \color {Red} \text {Factor out} (2x+1). \end{align*} \nonumber\]
Hence, \(30x^3 −21x^2 −18x =3x(5x−6)(2x + 1)\).
Check: First, use the FOIL shortcut to multiply the two binomial factors, then distribute the monomial factor.
\[\begin{align*} 3x(5x-6)(2x + 1) &= 3x(10x^2-7x-6) \quad \color {Red} \text {Apply the FOIL shortcut}\\ &= 3x^3-21x^2-18x \quad \color {Red} \text {Distribute the } 3x. \end{align*} \nonumber\]
Because this is the original polynomial, the solution checks.
Exercise \(\PageIndex{4}\)
Factor: \(12x^4 +2x^3 −30x^2\)
- Answer
-
\(2x^2(3x+5)(2x−3)\)
Nonlinear Equations Revisited
Let’s use the factoring technique of this chapter to solve some nonlinear equations.
Example \(\PageIndex{5}\)
Solve the equation \(2x^2 = 13 x−20\) both algebraically and graphically, then compare your answers.
Solution
Because there is a power of x larger than one, the equation is nonlinear. Make one side equal to zero.
\[\begin{align*} 2x^2 &= 13x-20 \quad \color {Red} \text {Original equation}\\2x^2-13x+20 &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber\]
Compare \(2x^2 −13x + 20\) with \(ax^2 + bx + c\) and note that \(a = 2\), \(b = −13\) and \(c = 20\). We need an integer pair whose product is \(ac = 40\) and whose sum is \(b = −13\). The integer pair \(−5\) and \(−8\) comes to mind. Write the middle term as a sum of like terms using this pair.
\[\begin{align*} 2x^2-5x-8x+20 &= 0 \quad \color {Red} -13x=-5x-8x\\x(2x-5)(2x-5) &= 0 \quad \color {Red} \text {Factor by grouping.}\\(x-4)(2x-5) &= 0 \quad \color {Red} \text {Factor out } 2x-5 \end{align*} \nonumber\]
We have a product that equals zero. Use the zero product property to complete the solution.
\[\begin{align*} x-4 &= 0 \\x & = 4 \end{align*} \nonumber\]
or
\[\begin{align*} 2x-5 &= 0 \\2x & = 5\\x & = \dfrac{5}{2} \end{align*} \nonumber\]
Thus, the solutions of \(2x^2 = 13x−20\) are \(x = 4\) and \(x =5 /2\).
Graphical solution:
Load each side of the equation \(2x^2 = 13x−20\) into the Y= menu of your graphing calculator, \(y =2x^2\) in \(\mathbb{Y1}\), \(y = 13 x−20\) in \(\mathbb{Y2}\)
(see Figure \(\PageIndex{1}\)). Select 6:ZStandard from the ZOOM menu to produce the image on the left in Figure 6.18. However, even after adjusting the WINDOW parameters (\(\mathbb{Xmin} =−10\), \(\mathbb{Xmax} = 10\), \(\mathbb{Ymin} = −10\), and \(\mathbb{Ymax} = 60\)), the image resulting from pushing the GRAPH button (see the image on the right in Figure \(\PageIndex{1}\)) does not clearly show the two points of intersection.
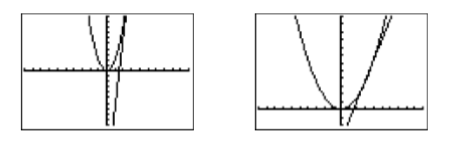
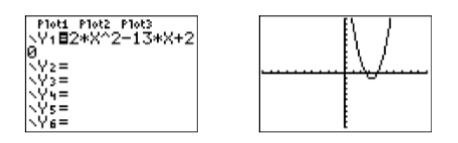
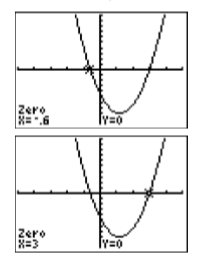
Let’s switch our strategy and work with the equation \(2x2 −13x + 20 = 0 \) instead. Load \(y =2x^2 − 13x + 20\) into \(\mathbb{Y1}\) in the Y= menu, then select 6:ZStandard from the ZOOM menu to produce the image at the right in Figure \(\PageIndex{2}\).
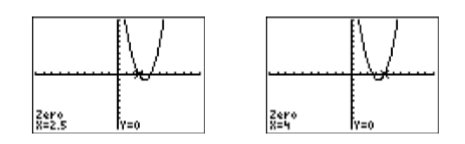
To find the solutions of \(2x^2−13x+20 = 0\), we must identify the \(x\)-intercepts of the graph in Figure \(\PageIndex{1}\). Select 2:zero from the CALC menu, then move the left- and right=arrows to move the cursor to the left of the first \(x\)-intercept. Press ENTER to mark the “Left bound,” then move the cursor to the right of the \(x\)-intercept and press ENTER to mark the “Right bound.” Finally, press ENTER to use the current position of the cursor for your “Guess.” The result is shown in the image on the left in Figure \(\PageIndex{3}\). Repeat the process to find the rightmost \(x\)-intercept. The result is shown in the image on the right in Figure \(\PageIndex{3}\).
Reporting the solution on your homework:
Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{4}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{4}\)).
- Label the graph with its equation (see Figure \(\PageIndex{4}\)).
- Drop dashed vertical lines through each \(x\)-intercept. Shade and label the \(x\)-values of the points where the dashed vertical line crosses the \(x\)-axis. These are the solutions of the equation \(2x^2 − 13x + 20 = 0\) (see Figure \(\PageIndex{4}\)).
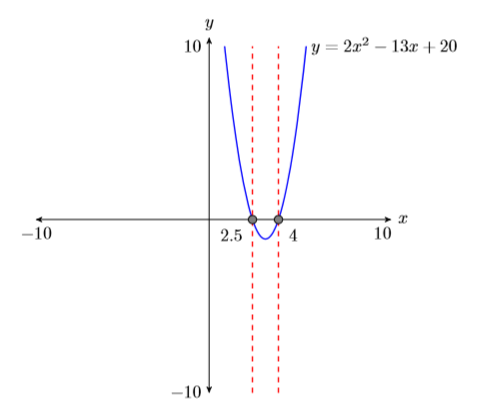
Finally, note how the graphical solutions of \(2x^2−13x+20=0\), namely \(x =2.5\) and \(x = 4\), match the solutions \(x =5 /2\) and \(x = 4\) found using the algebraic method. This is solid evidence that both methods of solution are correct. However, it doesn’t hurt to check the final answers in the original equation, substituting \(5/2\) for \(x\) and \(4\) for \(x\).
\[\begin{align*}
2x^2 &= 13x-20 \\
2\left (\dfrac{5}{2} \right )^2 & = 13\left (\dfrac{5}{2} \right ) -20\\
2\left (\dfrac{25}{4} \right ) & = 13\left (\dfrac{5}{2} \right ) -20\\
\dfrac{25}{2} & = \dfrac{65}{2} - \dfrac{40}{2}
\end{align*} \nonumber \]
and
\[\begin{align*} 2x^2 &= 13x-20 \\ 2(4)^2 & = 13(4) -20\\ 2(16) & = 13(4) -20\\ 32 & = 52 - 20 \end{align*} \nonumber\]
Because the last two statements are true statements, the solutions \(x =5 /2\) and \(x = 4\) check in the original equation \(2x^2 = 13x−20\).
Exercise \(\PageIndex{5}\)
Solve the equation \(5x^2 = 12x + 9\) both algebraically and graphically, then compare your answers.
- Answer
-
\(-3/5\), \(3\)
Example \(\PageIndex{6}\)
Solve the equation \(2x^3 + x^2 = 28x\) both algebraically and graphically, then compare your answers.
Solution
Because there is a power of x larger than one, the equation is nonlinear. Make one side equal to zero.
\[\begin{align*} 2x^3+x^2 &= 28x \quad \color {Red} \text {Original equation}\\2x^3+x^2-28x &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber\]
Note that the \(\mathrm {GCF}\) of \(2x^3\), \(x^2\), and \(28x\) is \(x\). Factor out \(x\).
\[x(2x^2 + x−28) = 0 \quad \color {Red} \text {Factor out the GCF} \nonumber \]
Compare \(2x^2+x−28\) with \(ax^2+bx+c\) and note that \(a = 2\), \(b = 1\) and \(c = −28\). We need an integer pair whose product is \(ac = −56\) and whose sum is \(b = 1\). The integer pair \(−7\) and \(8\) comes to mind. Write the middle term as a sum of like terms using this pair.
\[\begin{align*} x(2x^2-7x+8x-28) &= 0 \quad \color {Red} x=-7x+8x\\x[x(2x-7)+4(2x-7)] &= 0 \quad \color {Red} \text {Factor by grouping.}\\x(x+4)(2x-7) &= 0 \quad \color {Red} \text {Factor out } 2x-7. \end{align*} \nonumber\]
We have a product of three factors that equals zero. By the zero product property, at least one of the factors must equal zero.
\[x=0 \nonumber \]
or
\[\begin{align*} x+4 &= 0 \\x & = -4 \end{align*} \nonumber\]
or
\[\begin{align*} 2x-7 & = 0 \\ 2x & = 7\\ x & = \dfrac{7}{2} \end{align*} \nonumber\]
Thus, the solutions of \(2x^3 + x^2 = 28x\) are \(x = 0\), \(x =−4\), and \(x =7 /2\).
Graphical solution:
Rather than working with \(2x^3+x^2 = 28x\), graphing each side separately and finding where the graphs intersect, we will work instead with \(2x^3 + x^2 − 28x = 0\), locating where the graph of \(y =2x^3 + x^2 − 28x\) crosses the \(x\)-axis. Load \(y =2x^3 + x^2 −28x\) into \(\mathbb{Y1}\) in the Y= menu, then select 6:ZStandard from the ZOOM menu to produce the image at the right in Figure \(\PageIndex{5}\).
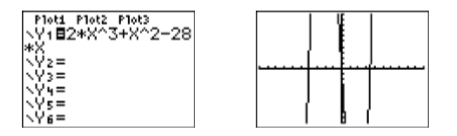
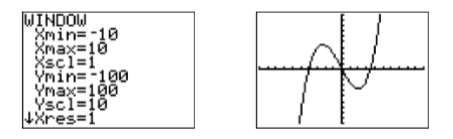
In the image at the right in Figure \(\PageIndex{6}\), we saw the graph rise from the bottom of the screen, leave the top of the screen, return and leave via the bottom of the screen, and then finally return and leave via the top of the screen. Clearly, there are at least two turning points to the graph that are not visible in the current viewing window. Set the WINDOW settings as shown in the image on the left in Figure \(\PageIndex{6}\), then push the GRAPH button to produce the image on the right in Figure \(\PageIndex{6}\). Note that this window now shows the \(x\)-intercepts as well as the turning points of the graph of the polynomial.
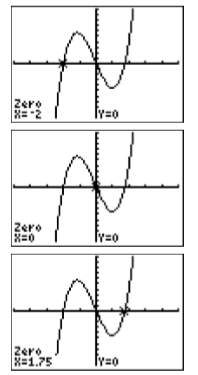
To find the solutions of \(2x^3 + x2 −28x = 0\), we must identify the \(x\)-intercepts of the graph in Figure \(\PageIndex{6}\). Select 2:zero from the CALC menu, then use the left- and right-arrow keys to move the cursor to the left of the first \(x\)-intercept. Press ENTER to mark the “Left bound,” then move the cursor to the right of the \(x\)-intercept and press ENTER to mark the “Right bound.” Finally, press ENTER to use the current position of the cursor for your “Guess.” The result is shown in the first image on the left in Figure \(\PageIndex{7}\). Repeat the process to find the remaining \(x\)-intercepts. The results are shown in the next two images in Figure \(\PageIndex{7}\).
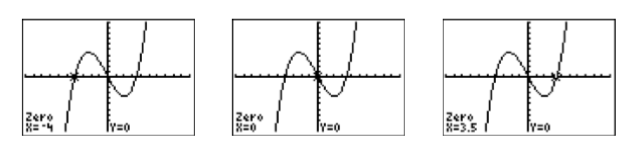
Reporting the solution on your homework:
Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{8}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{8}\)).
- Label the graph with its equation (see Figure \(\PageIndex{8}\)).
- Drop dashed vertical lines through each \(x\)-intercept. Shade and label the \(x\)-values of the points where the dashed vertical line crosses the \(x\)-axis. These are the solutions of the equation \(2x^3 + x^2 −28x = 0\) (see Figure \(\PageIndex{8}\)).
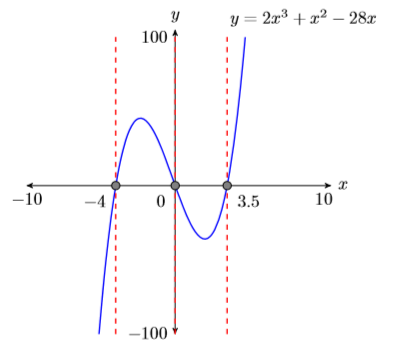
Finally, note how the graphical solutions of \(2x^3+x^2−28x = 0\), namely \(x =−4\), \(x = 0\), and \(x =3.5\), match the solutions \(x = −4\), \(x = 0\), and \(x =7 /2\) found using the algebraic method.
Exercise \(\PageIndex{6}\)
Solve the equation \(4x^3 = −x^2 + 14x\) both algebraically and graphically, then compare your answers.
- Answer
-
\(−2\), \(0\), \(7/4\)