6.5: Factoring Special Forms

In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial.

Squaring a binomial

Here are two earlier rules for squaring a binomial.

1. $(a + b)^2 = a^2 +2ab + b^2$
2. $(a−b)^2 = a^2 −2ab + b^2$

Perfect Square Trinomials

To square a binomial such as $(a + b)^2$, proceed as follows:

1. Square the first term: $a$
2. Multiply the first and second term, then double: $2ab$
3. Square the last term: $b^2$

Example $\PageIndex{1}$

Expand: $(2x +3y)^2$

Solution

Using the pattern $(a+b)^2 = a^2+2ab+b^2$, we can expand $(2x+3y)^2$ as follows:

$$\begin{align*} (2x +3y)^2 &= (2x)^2 + 2(2x)(3y) + (3y)^2 \\ &= 4x^2 +6xy +9y^2 \end{align*} \nonumber$$

Note how we square the first and second terms, then produce the middle term of our answer by multiplying the first and second terms and doubling.

Exercise $\PageIndex{1}$

Expand: $(5a +2b)^2$

Answer

$25a^2 + 20ab +4b^2$

Example $\PageIndex{2}$

Expand: $(3u^2 −5v2)^2$

Solution

Using the pattern $(a−b)^2 = a^2−2ab+b^2$, we can expand $(3u^2−5v^2)^2$ as follows:

$$\begin{align*} (3u^2 -5v^2)^2 &= (3u^2)^2 - 2(3u^2)(5v^2) + (5v^2)^2 \\ &= 9u^4 - 30u^2v^2 + 25v^4 \end{align*} \nonumber$$

Note that the sign of the middle term is negative this time. The first and last terms are still positive because we are squaring.

Exercise $\PageIndex{2}$

Expand: $(2s^3 −7t)^2$

Answer

$4s^6 −28s^3t + 49t^2$

Once you’ve squared a few binomials, it’s time to do all of the work in your head.

1. Square the first term.
2. Multiply the first and second term and double the result.
3. Square the second term.

Example $\PageIndex{3}$

Expand each of the following:

1. $(2y−3)^2$
2. $(4a−3b)^2$
3. $(x3 + 5)^2$

Solution

Using the pattern $(a ± b)^2 = a^2 ± 2ab + b^2$, we expand each binomially mentally, writing down the answer without any intermediate steps.

1. $(2y−3)^2 = 4y^2 −12y +9$
2. $(4a−3b)^2 = 16a^2 −24ab +9b^2$
3. $(x^3 + 5)^2 = x^6 + 10x^3 + 25$

Exercise $\PageIndex{3}$

Expand: $(5x^4 −3)^2$

Answer

$25x^8 −30x^4 +9$

Now, because factoring is “unmultiplying,” it should be a simple matter to reverse the process of Example $\PageIndex{3}$.

Example $\PageIndex{4}$

Factor each of the following trinomials:

1. $4y^2 −12y + 9$
2. $16a^2 −24ab +9b^2$
3. $x^6 + 10x^3 + 25$

Solution

Because of the work already done in Example $\PageIndex{3}$, it is a simple task to factor each of these trinomials.

1. $4y^2 −12y + 9 = (2y−3)^2$
2. $16a^2 −24ab +9b^2 = (4 a−3b)^2$
3. $x^6 + 10x^3 + 25 = (x^3 + 5)$

Exercise $\PageIndex{4}$

Factor: $25x^8 −30x^4 +9$

Answer

$(5x^4 −3)^2$

Each of the trinomials in Example $\PageIndex{4}$ is an example of a perfect square trinomial.

Perfect square trinomial

If a trinomial $a^2 +2ab + b^2$ is the square of a binomial, as in $(a+b)^2$, then the trinomial is called a perfect square trinomial.

So, how does one recognize a perfect square trinomial? If the first and last terms of a trinomial are perfect squares, then you should suspect that you may be dealing with a perfect square trinomial. However, you also have to have the correct middle term in order to have a perfect square trinomial.

Table $\PageIndex{1}$: List of Squares

$n$	$n^2$
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144
13	169
14	196
15	225
16	256
17	289
18	324
19	361
20	400
21	441
22	484
23	529
24	576
25	625

Example $\PageIndex{5}$

Factor each of the following trinomials:

1. $9x^2 −42x + 49$
2. $49a^2 + 70ab + 25b^2$
3. $4x^2 −37x +9$

Solution

Note that the first and last terms of each trinomial are perfect squares.

1. In the trinomial $9x^2−42x+49$, note that $(3x)^2 =9x^2$ and $72 = 49$. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that $9x^2 −42x + 49$ factors as follows: $$9x^2 −42x + 49 \overset{?}{=} (3x−7)^2 \nonumber$$ However, we must check to see if the middle term is correct. Multiply $3x$ and $7$, then double: $2(3x)(7) = 42x$. Thus, the middle term is correct and therefore $$9x^2 −42x + 49 = (3x−7)^2\nonumber$$
2. In the trinomial $49a^2+70ab+25b^2$, note that $(7a)^2 = 49a^2$ and $(5b)^2 = 25 b^2$. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that $49a^2 + 70ab + 25 b^2$ factors as follows: $$49a^2 + 70ab + 25 b^2 \overset{?}{=} (7 a +5 b)^2 \nonumber$$ However, we must check to see if the middle term is correct. Multiply $7a$ and $5b$, then double: $2(7a)(5b) = 70ab$. Thus, the middle term is correct and therefore $$49a^2 + 70ab + 25 b^2 = (7 a +5 b)^2 \nonumber$$
3. In the trinomial $4x^2−37x+9$, note that $(2x)^2 =4x^2$ and $(3)^2 = 9$. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that $4x^2 −37x + 9$ factors as follows: $$4x^2 −37x +9 \overset{?}{=} (2x−3)^2 \nonumber$$

However, we must check to see if the middle term is correct. Multiply $2x$ and $3$, then double: $2(2x)(3) = 12x$. However, this is not the middle term of $4x^2 −37x + 9$, so this factorization is incorrect! We must find another way to factor this trinomial.

Comparing $4x^2 −37x+ 9$ with $ax^2 + bx+ c$, we need a pair of integers whose product is $ac = 36$ and whose sum is $b = −37$. The integer pair $−1$ and $−36$ comes to mind. Replace the middle term as a sum of like terms using this ordered pair.

$$\begin{align*} 4x^2-37x +9 &= 4x^2-x-36x +9 \quad \color {Red} -37x=-x-36x\\ &= x(4x-1)-9(4x-1) \quad \color {Red} \text {Factor by grouping}\\ &= (x-9)(4x-1) \quad \color {Red} \text {Factor out } 4x-1 \end{align*} \nonumber$$

This example clearly demonstrates how important it is to check the middle term.

Exercise $\PageIndex{5}$

Factor: $16x^2 + 72x + 81$

Answer

$(4x + 9)^2$

Remember the first rule of factoring!

The first rule of factoring

The first step to perform in any factoring problem is factor out the $\mathrm{GCF}$.

Example $\PageIndex{6}$

Factor each of the following trinomials:

1. $2x^3y + 12x^2y^2 + 18xy^3$
2. $−4x^5 + 32x^4 −64x^3$

Solution

Remember, first factor out the $\mathrm{GCF}$.

1. In the trinomial $2x^3y + 12x^2y^2 + 18xy^3$, we note that the $\mathrm{GCF}$ of $2x^3y$, $12x^2y^2$, and $18xy^3$ is $2xy$. We first factor out $2xy$. $$2x^3y + 12x^2y^2 + 18xy^3 =2xy(x^2 +6xy +9y^2) \nonumber$$ We now note that the first and last terms of the resulting trinomial factor are perfect squares, so we take their square roots and factors as follows. $$=2xy(x +3y)^2 \nonumber$$ Of course, the last factorization is correct only if the middle term is correct. Because $2(x)(3y)=6xy$ matches the middle term of $x^2 +6xy +9y^2$, we do have a perfect square trinomial and our result is correct.
2. In the trinomial $−4x^5 + 32x^4 −64x^3$, we note that the $\mathrm{GCF}$ of $4x^5$, $32x^4$, and $64x^3$ is $4x^3$. We first factor out $4x^3$. $$−4x^5 + 32x^4 −64x^3 =4x^3(−x^2 +8x−16) \nonumber$$ However, the first and third terms of $−x^2 +8x−16$ are negative, and thus are not perfect squares. Let’s begin again, this time factoring out $−4x^3$. $$−4x^5 + 32x^4 −64x^3 = −4x^3(x^2 −8x + 16) \nonumber$$ This time the first and third terms of $x^2−8x+16$ are perfect squares. We take their square roots and write: $$= −4x^3(x−4)^2 \nonumber$$ Again, this last factorization is correct only if the middle term is correct. Because $2(x)(4) = 8x$, we do have a perfect square trinomial and our result is correct.

Exercise $\PageIndex{6}$

Factor: $−4x^3 −24x^2 −36x$

Answer

$−4x(x + 3)^2$

The Difference of Squares

The second special product form we learned in Chapter 5 was the difference of squares.

The difference of squares

Here is the difference of squares rule. $$(a + b)(a−b)=a^2 − b^2 \nonumber$$

If you are multiplying two binomials which have the exact same terms in the “First” positions and the exact same terms in the “Last” positions, but one set is separated by a plus sign while the other set is separated by a minus sign, then multiply as follows:

1. Square the first term: $a^2$
2. Square the second term: $b^2$
3. Place a minus sign between the two squares.

Example $\PageIndex{7}$

Expand each of the following:

1. $(3x+5)(3x-5)$
2. $(a^3 −2b^3)(a^3 +2b^3)$

Solution

We apply the difference of squares pattern to expand each of the given problems.

1. In $(3x + 5)(3x − 5)$, we have the exact same terms in the “First” and “Last” positions, with the first set separated by a plus sign and the second set separated by a minus sign.
   1. Square the first term: $(3x)^2 =9x^2$
   2. Square the second term: $5^2 = 25$
   3. Place a minus sign between the two squares.

Hence: $$(3x + 5)(3x−5) = 9x^2 −25 \nonumber$$

2. In $(a^3 −2b^3)(a^3 +2b^3)$, we have the exact same terms in the “First” and “Last” positions, with the first set separated by a minus sign and the second set separated by a plus sign.
   1. Square the first term: $(a^3)^2 = a^6$
   2. Square the second term: $(2b^3)^2 =4b^6$
   3. Place a minus sign between the two squares.

Hence: $$(a^3 −2b^3)(a^3 +2b^3)=a^6 −4b^6 \nonumber$$

Exercise $\PageIndex{7}$

Expand: $(4x−3y)(4x +3y)$

Answer

$16x^2 −9y^2$

Because factoring is “unmultiplying,” is should be a simple matter to reverse the process of Example $\PageIndex{7}$.

Example $\PageIndex{8}$

Factor each of the following:

1. $9x^2 −25$
2. $a^6 −4b^6$

Solution

Because of the work already done in Example $\PageIndex{7}$, it is a simple matter to factor (or “unmultiply”) each of these problems.

1. $9x^2 −25 = (3x + 5)(3x−5)$
2. $a^6 −4b^6 =(a^3 −2b^3)(a^3 +2b^3)$

In each case, note how we took the square roots of each term, then separated one set with a plus sign and the other with a minus sign. Because of the commutative property of multiplication, it does not matter which one you make plus and which one you make minus.

Exercise $\PageIndex{8}$

Factor: $81x^2 −49$

Answer

$(9x + 7)(9x−7)$

Always remember the first rule of factoring.

Example $\PageIndex{9}$

Factor: $x^3 −9x$

Solution

In $x^3 −9x$, the $\mathrm{GCF}$ of $x^3$ and $9x$ is $x$. Factor out $x$. $$x^3−9x = x(x^2 −9) \nonumber$$ Note that $x^2−9$ is now the difference of two perfect squares. Take the square roots of $x^2$ and $9$, which are $x$ and $3$, then separate one set with a plus sign and the other set with a minus sign.
$$= x(x + 3)(x−3) \nonumber$$

Exercise $\PageIndex{9}$

Factor: $4x^4−16x^2$

Answer

$4x^2(x + 2)(x−2)$

Factoring Completely

Sometimes after one pass at factoring, factors remain that can be factored further. You must continue to factor in this case.

Example $\PageIndex{10}$

Factor: $x^4 −16$

Solution

In $x^4 −16$, we have the difference of two squares: $(x^2)^2 = x^4$ and $4^2 = 16$. First, we take the square roots, then separate one set with a plus sign and the other set with a minus sign. $$x^4 −16 = (x^2 + 4)(x^2 −4) \nonumber$$ Note that $x^2+4$ is the sum of two squares and does not factor further. However, $x^2 −4$ is the difference of two squares. Take the square roots, $x$ and $2$, then separate one set with a plus sign and the other set with a minus sign.
$$=( x^2 + 4)(x + 2)(x−2) \nonumber$$ Done. We cannot factor further.

Exercise $\PageIndex{10}$

Factor: $x^4 −81$

Answer

$(x^2 + 9)(x + 3)(x−3)$

Nonlinear Equations Revisited

Remember, if an equation is nonlinear, the first step is to make one side equal to zero by moving all terms to one side of the equation. Once you’ve completed this important first step, factor and apply the zero product property to find the solutions.

Example $\PageIndex{11}$

Solve for $x$: $25x^2 = 169$

Solution

Make one side equal to zero, factor, then apply the zero product property.

$$\begin{align*} 25x^2 &= 169 \quad \color {Red} \text {Original equation.}\\ 25x^2 - 169 &= 0 \quad \color {Red} \text {Subtract 169 from both sides.} \end{align*} \nonumber$$

Note that we have two perfect squares separated by a minus sign. This is the difference of squares pattern. Take the square roots, making one term plus and one term minus.

$$\begin{align*} (5x + 13)(5x-13) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber$$

Use the zero product property to complete the solution, setting each factor equal to zero and solving the resulting equations.

$$\begin{align*} 5x + 13 &= 0 \\ x &= -\dfrac{13}{5} \end{align*} \nonumber$$

or

$$\begin{align*} 5x - 13 &= 0 \\ x &= \dfrac{13}{5} \end{align*} \nonumber$$

Hence, the solutions of $25x^2 = 169$ are $x =−13/5$ and $x = 13 /5$. We encourage readers to check each of these solutions.

Exercise $\PageIndex{11}$

Solve for $x$: $16x^2 = 121$

Answer

$−11/4$, $11/4$

Example $\PageIndex{12}$

Solve for $x$: $49x^2 + 81 = 126x$

Solution

Make one side equal to zero, factor, then apply the zero product property.

$$\begin{align*} 49x^2+81x &= 126x \quad \color {Red} \text {Original equation.}\\ 49x^2-126x+81 &= 0 \quad \color {Red} \text {Subtract 126x from both sides.} \end{align*} \nonumber$$

Note that the first and last terms of the trinomial are perfect squares. Hence, it make sense to try and factor as a perfect square trinomial, taking the square roots of the first and last terms.

$$\begin{align*} (7x-9)^2 &= 0 \quad \color {Red} \text {Factor as a perfect square trinomial.} \end{align*} \nonumber$$

Of course, be sure to check the middle term. Because $−2(7x)(9) = −126x$, the middle term is correct. Because $(7x−9)^2 = (7 x−9)(7x−9)$, we can use the zero product property to set each factor equal to zero and solve the resulting equations.

$$\begin{align*} 7x-9 &= 0 \\ x &= \dfrac{9}{7} \end{align*} \nonumber$$

or

$$\begin{align*} 7x-9 &= 0 \\ x &= \dfrac{9}{7} \end{align*} \nonumber$$

Hence, the only solution of $49x^2 +81 = 126x$ is $x =9 /7$. We encourage readers to check this solution.

Note

One can also argue that the only number whose square is zero is the number zero. Hence, one can go directly from $(7x−9)^2 =0$ to $7x−9=0$. Hence, the only solution of $49x^2 + 81 = 126x$ is $x =9 /7$.

Exercise $\PageIndex{12}$

Solve for $x$: $25x^2 = 80x−64$

Answer

$8/5$

Example $\PageIndex{13}$

Solve for $x$: $2x^3 +3x^2 = 50x + 75$

Solution

Make one side equal to zero, factor, then apply the zero product property.

$$\begin{align*} 2x^3 +3x^2 &= 50x + 75 \quad \color {Red} \text {Original equation.}\\ 2x^3 + 3x^2 - 50x - 75 &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber$$

This is a four-term expression, so we try factoring by grouping. Factor $x^2$ out of the first two terms, and $−25$ out of the second two terms.

$$\begin{align*} x^2(2x + 3)-25(2x + 3) &= 0 \quad \color {Red} \text {Factor by grouping}\\ (x^2-25)(2x + 3) &= 0 \quad \color {Red} \text {Factor out } 2x+3 \end{align*} \nonumber$$

Complete the factorization by using the difference of squares to factor $x^2−25$.

$$\begin{align*} (x+5)(x-5)(2x+3) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber$$

Finally, use the zero product property. Set each factor equal to zero and solve for $x$.

$$\begin{align*} x+5 &= 0 \\ x &= -5 \end{align*} \nonumber$$

or

$$\begin{align*} x-5 &= 0 \\ x &= 5 \end{align*} \nonumber$$

or

$$\begin{align*} 2x+3 &= 0 \\ x &= -\dfrac{3}{2} \end{align*} \nonumber$$

Hence, the solutions of $2x^3 +3x^2 = 50x+75$ are $x = −5$, $x = 5$, and $x = −3/2$. We encourage readers to check each of these solutions.

Exercise $\PageIndex{13}$

Solve for $x$: $5x^3 + 36 =x^2 + 180x$

Answer

$−6$, $6$, $1/5$

Let’s solve another nonlinear equation, matching the algebraic and graphical solutions.

Example $\PageIndex{14}$

Solve the equation $x^3 =4x$, both algebraically and graphically, then compare your answers.

Solution

Note that we have a power of $x$ larger than one, so the equation $x^3 =4x$ is nonlinear. Make one side zero and factor.

$$\begin{align*} x^3 &= 4x \quad \color {Red} \text {Original equation.}\\ x^3-4x &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero. }\\ x(x^2-4) &=0 \quad \color {Red} \text {Factor out GCF.}\\ x(x+2)(x-2) &= 0 \quad \color {Red} \text {Apply difference of squares.} \end{align*} \nonumber$$

Note that we now have a product of three factors that equals zero. The zero product property says that at least one of these factors must equal zero.

$$\begin{align*} x &= 0 \end{align*} \nonumber$$

or

$$\begin{align*} x+2 &= 0 \\ x &= -2 \end{align*} \nonumber$$

or

$$\begin{align*} x-2 &= 0 \\ x &= 2 \end{align*} \nonumber$$

Hence, the solutions of $x^3 =4x$ are $x = 0$, $x = −2$, and $x = 2$.

Graphical solution

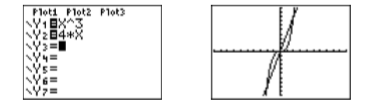
Load $y = x^3$ and $y =4x$ into $\mathbb{Y1}$ and $\mathbb{Y2 }$in the Y= menu of your calculator. Select 6:ZStandard from the ZOOM menu to produce the graph in Figure $\PageIndex{1}$.

Although the image in Figure $\PageIndex{1}$ shows all three points of intersection, adjusting the WINDOW parameters as shown in Figure $\PageIndex{2}$, then pressing the GRAPH button will produce a nicer view of the points of intersection, as shown in the figure on the right in Figures $\PageIndex{2}$.

Figure $\PageIndex{1}$: Sketching $y = x^3$ and $y =4x$.

Figure $\PageIndex{2}$: Adjusting the viewing window.

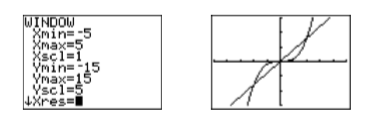
Use the 5:intersect tool from the CALC menu to find the three points of intersection. Press the ENTER key in response to “First curve,” then press ENTER again in response to “Second curve,” then use the left-arrow key to move your cursor close to the leftmost point of intersection and press ENTER in response to “Guess.” The result is shown in the first image on the left in Figure $\PageIndex{3}$. Repeat the process to find the remaining points of intersection. The results are shown in the last two images in Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: Finding the points of intersection.

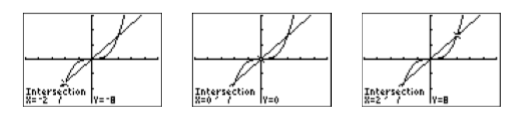
Thus, the graphical solutions are $x =−2$, $x = 0$, and $x = 2$.

Reporting the solution on your homework:

Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.

• Label the horizontal and vertical axes with $x$ and $y$, respectively (see Figure $\PageIndex{4}$).
• Place your WINDOW parametersat the end of each axis (see Figure $\PageIndex{4}$).
• Label the graph with its equation (see Figure $\PageIndex{4}$).
• Drop dashed vertical lines through each $x$-intercept. Shade and label the $x$-values of the points where the dashed vertical line crosses the $x$-axis. These are the solutions of the equation $x^3 = 4x$ (see Figure $\PageIndex{4}$).

Figure $\PageIndex{4}$: Reporting your graphical solution on your homework.

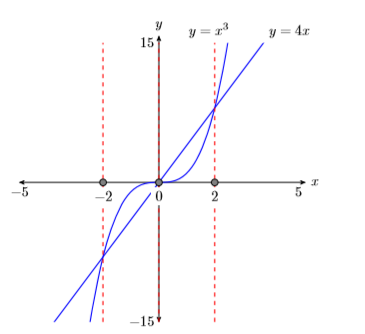
Finally, note that the graphical solutions $x = −2$, $x = 0$, and $x = 2$ match our algebraic solutions exactly.

Exercise $\PageIndex{14}$

Solve the equation $x^3 = 16x$ both algebraically and graphically, then compare your answers.

Answer

$−4$, $0$, $4$