6.6: Factoring Strategy

When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because they are similar, seem to flow. However, when you encounter a mixture of factoring problems of different types, progress is harder. The goal of this section is to set up a strategy to follow when attacking a general factoring problem.

If it hasn’t already been done, it is helpful to arrange the terms of the given polynomial in some sort of order (descending or ascending). Then you want to apply the following guidelines.

Factoring Strategy

These steps should be followed in the order that they appear.

1. Factor out the greatest common factor (\(\mathrm{GCF}\)).
2. Look for a special form.
   1. If you have two perfect squares separated by a minus sign, use the difference of squares pattern to factor: \[a^2 −b^2 =(a + b)(a−b)\nonumber \]
   2. If you have a trinomial whose first and last terms are perfect squares, you should suspect that you have a perfect square trinomial. Take the square roots of the first and last terms and factor as follows.\[a^2 +2ab + b^2 =(a + b)^2 \nonumber \]Be sure to check that the middle term is correct.
3. If you have a trinomial of the form \(ax^2 + bx + c\), use the \(ac\)-method to factor.
4. If you have a four-term expression, try to factor by grouping.

Once you’ve applied the above strategy to the given polynomial, it is quite possible that one of your resulting factors will factor further. Thus, we have the following rule.

Factor completely

The factoring process is not complete until none of your remaining factors can be factored further. This is the meaning of the phrase, “factor completely.”

Finally, a very good word of advice.

Check your factoring by multiplying

Once you’ve factored the given polynomial completely, it is a very good practice to check your result. If you multiply to find the product of your factors, and get the original given polynomial as a result, then you know your factorization is correct.

It’s a bit more work to check your factorization, but it’s worth the effort. It helps to eliminate errors and also helps to build a better understanding of the factoring process. Remember, factoring is “unmultiplying,” so the more you multiply, the better you get at factoring.

Let’s see what can happen when you don’t check your factorization!

Warning! The following solution is incorrect!

Factor: \(2x^4 +8x^2\)

Solution: Factor out the \(\mathrm{GCF}\)

\[\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ &= 2x^2(x+2)^2 \end{align*} \nonumber\]

Note that this student did not bother to check his factorization. Let’s do that for him now.

Check: Multiply to check. Remember, when squaring a binomial, there is a middle term.

\[\begin{align*} 2x^2(x+2)^2 &= 2x^2(x^2+4x+4) \\ &= 2x^4+8x^3+8x^2 \end{align*} \nonumber\]

This is not the same as the original polynomial \(2x^4 +8x^2\), so the student’s factorization is incorrect. Had the student performed this check, he might have caught his error, provided of course, that he multiplies correctly during the check.

The correct factorization follows.

\[\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ \end{align*} \nonumber\]

The sum of squares does not factor, so we are finished.

Check: Multiply to check.

\[\begin{align*} 2x^2(x^2+4) &= 2x^4+8x^2\\ \end{align*} \nonumber\]

This is the same as the original polynomial \(2x^4 +8x^2\), so this factorization is correct.

Example \(\PageIndex{1}\)

Factor completely: \(−3x^6 +3x^2\)

Solution

The first rule of factoring is “Factor out the GCF.” The \(\mathrm{GCF}\) of \(−3x^6\) and \(3x^2\) is \(3x^2\), so we could factor out \(3x^2\).\[−3x^6 +3x^2 =3x^2(−x^4 + 1) \nonumber \]This is perfectly valid, but we don’t like the fact that the second factor starts with \(−x^4\). Let’s factor out \(−3x^2\) instead.\[−3x^6 +3x^2 = −3x^2(x^4 −1) \nonumber \]The second factor is the difference of two squares. Take the square roots, separating one pair with a plus sign, one pair with a minus sign. \[= −3x^2(x^2 + 1)(x^2 −1) \nonumber \] The sum of squares does not factor. But the last factor is the difference of two squares. Take the square roots, separating one pair with a plus sign, one pair with a minus sign.\[= −3x^2(x^2 + 1)(x + 1)(x−1) \nonumber \]

Check: Multiply to check the result.

\[\begin{align*} -3x^2(x^2+1)(x+1)(x-1) &= -3x^2(x^2+1)(x^2-1)\\ &= -3x^2(x^4-1)\\ &= -3x^6+3x^2 \end{align*} \nonumber\]

The factorization checks.

Exercise \(\PageIndex{1}\)

Factor completely: \(−4x^7 + 64x^3\)

Answer

\(−4x^3(x^2 + 4)(x + 2)(x−2)\)

Example \(\PageIndex{2}\)

Factor completely: \(x^3y +9xy^3 +6x^2y^2\)

Solution

The first rule of factoring is “Factor out the GCF.” The \(\mathrm{GCF}\) of \(x^3y\), \(9xy^3\), and \(6x^2y^2\) is \(xy\), so we factor out \(xy\).\[x^3y +9xy^3 +6x^2y^2 = xy(x^2 +9y^2 +6xy) \nonumber \]Let’s order that second factor in descending powers of \(x\).\[= xy(x^2 +6xy +9y^2) \nonumber \]The first and last terms of the trinomial factor are perfect squares. We suspect we have a perfect square trinomial, so we take the square roots of the first and last terms, check the middle term, and write:\[= xy(x +3y)^2 \nonumber \]Thus, \(x^3y +9xy^3 +6x^2y^2 = xy(x +3y)^2\).
Check: Multiply to check the result.\[\begin{align*} xy(x+3y)^2 &= xy(x^2 +6xy +9y^2)\\ &= x^3y+6x^2y^2 +9xy^3 \end{align*} \nonumber\]
Except for the order, this result is the same as the given polynomial. The factorization checks.

Exercise \(\PageIndex{2}\)

Factor completely: \(3a^2b^4 + 12a^4b^2 −12a^3b^3\)

Answer

\(3a^2b^2(2a−b)^2\)

Example \(\PageIndex{3}\)

Factor completely: \(2x^3 −48x + 20x^2\)

Solution

In the last example, we recognized a need to rearrange our terms after we pulled out the \(\mathrm{GCF}\). This time, let’s arrange our terms in descending powers of \(x\) right away.\[2x^3 −48x + 20x^2 =2x^3 + 20x^2 −48x \nonumber \]Now, let’s factor out the \(\mathrm{GCF}\).\[=2x(x^2 + 10x−24) \nonumber \] The last term of the trinomial factor is not a perfect square. Let’s move to the ac-method to factor. The integer pair \(−2,12\) has a product equal to \(ac = −24\) and a sum equal to \(b = 10\). Because the coefficient of \(x^2\) is one, this is a “drop in place” situation. We drop our pair in place and write:\[=2x(x−2)(x + 12) \nonumber \] Thus, \(2x^3 −48x + 20x^2 =2x(x−2)(x + 12)\).

Check: Multiply to check the result. We use the FOIL method shortcut and mental calculations to speed things up.\[\begin{align*} 2x(x-2)(x + 12) &= 2x(x^2+10x-24) \\ &= 2x^3 + 20x^2 - 48x \end{align*} \nonumber\]Except for the order, this result is the same as the given polynomial. The factorization checks.

Exercise \(\PageIndex{3}\)

Add exercises text here.

Answer

\(−3x^2(x−4)(x−5)\)

Example \(\PageIndex{4}\)

Factor completely: \(2a^2 −13ab−24b^2\)

Solution

There is no common factor we can factor out. We have a trinomial, but the first and last terms are not perfect squares, so let’s apply the \(ac\)-method. Ignoring the variables for a moment, we need an integer pair whose product is \(ac = −48\) and whose sum is \(−13\). The integer pair \(3,−16\) comes to mind (if nothing comes to mind, start listing integer pairs). Break up the middle term into a sum of like terms using the integer pair \(3,−16\), then factor by grouping

\[\begin{align*} 2a^2-13ab-24b^2 &= 2a^2 +3ab-16ab-24b^2 \\ &= a(2a+3b)-8b(2a+3b)\\ &= (a-8b)(2a+3b) \end{align*} \nonumber\]

Thus, \(2a^2-13ab-24b^2 =( a−8b)(2a +3 b)\).

Check: Multiply to check the result. We use the FOIL method shortcut and mental calculations to speed things up.\[(a−8b)(2a +3 b)=2a^2 −13ab−24b^2 \nonumber \] This result is the same as the given polynomial. The factorization checks.

Exercise \(\PageIndex{4}\)

Factor completely: \(8x^2 + 14xy−15y^2\)

Answer

\((2 x +5y)(4x−3y)\)

Example \(\PageIndex{5}\)

Factor completely: \(30x^4 + 38x^3 −20x^2\)

Solution

The first step is to factor out the \(\mathrm{GCF}\), which in this case is \(2x^2\).\[30x^4 + 38x^3 −20x^2 =2x^2(15x^2 + 19x−10) \nonumber \]The first and last terms of the trinomial factor are not perfect squares, so let’s move again to the \(ac\)-method. Comparing \(15x^2+19x−10\) with \(ax^2+bx+c\), note that \(ac = (15)(−10) = −150\). We need an integer pair whose product is \(−150\) and whose sum is \(19\). The integer pair \(−6\) and \(25\) satisfies these requirements. Because \(a \neq 1\), this is not a “drop in place” situation, so we need to break up the middle term as a sum of like terms using the pair \(−6\) and \(25\).\[=2x^2(15x^2 −6x + 25x−10) \nonumber \]Factor by grouping. Factor \(3x\) out of the first two terms and \(5\) out of the third and fourth terms.\[=2x^2(3x(5x−2) + 5(5x−2)) \nonumber \]Finally, factor out the common factor \(5x−2\).\[=2x^2(3x + 5)(5x−2) \nonumber \]Thus, \(30x^4 + 38x^3 −20x^2 =2x^2(3x + 5)(5x−2)\).

Check: Multiply to check the result. Use the FOIL method to first multiply the binomials.\[2x^2(3x + 5)(5x−2) = 2x^2(15x^2 + 19x−10) \nonumber \]Distribute the \(2x^2\).\[= 30x^4 + 38x^3 −20x^2 \nonumber \]This result is the same as the given polynomial. The factorization checks.

Exercise \(\PageIndex{5}\)

Factor completely: \(36x^3 + 60x^2 +9x\)

Answer

\(3x(6x + 1)(2x + 3)\)

Example \(\PageIndex{6}\)

Factor completely: \(8x^5 + 10x^4 −72x^3 −90x^2\)

Solution

Each of the terms is divisible by \(3x^3\). Factor out \(3x^3\).\[15x^6 −33x^5 −240x^4 + 528x^3 =3x^3[5x^3 −11x^2 −80x + 176] \nonumber \]The second factor is a four-term expression. Factor by grouping.

\[\begin{align*} &= 3x^3[x^2(5x-11)-16(5x-11)] \\ &= 3x^3(x^2-16)(5x-11) \end{align*} \nonumber\]

The factor \(x^2−16\) is a difference of two squares. Take the square roots, separate one pair with a plus, one pair with a minus.\[=3x^3(x + 4)(x−4)(5x−11) \nonumber \] Thus, \(15x^6 −33x^5 −240x^4 + 528x^3 =3x^3(x + 4)(x−4)(5x−11)\).

Check: Multiply to check the result.

\[\begin{align*} 3x^3(x + 4)(x-4)(5x-11) &= 3x^3(x^2-16)(5x-11) \\ &= 3x^3(5x^3 - 11x^2 - 80x + 176 \\ &= 15x^6 - 33x^5 - 240x^4 + 528x^3 \end{align*} \nonumber\]

This result is the same as the given polynomial. The factorization checks.

Exercise \(\PageIndex{6}\)

Factor completely: \(15x^6−33x^5−240x^4 +528x^3\)

Answer

\(2x^2(x−3)(x + 3)(4x + 5)\)

Using the Calculator to Assist the \(ac\)-Method

When using the \(ac\)-method to factor \(ax^2+bx+c\) and \(ac\) is a very large number, then it can be difficult to find a pair whose product is \(ac\) and whose sum in \(b\). For example, consider the trinomial:\[12y^2 −11y−36 \nonumber \]We need an integer pair whose product is \(ac =−432\) and whose sum is \(b = −11\). We begin listing integer pair possibilities, but the process quickly becomes daunting.

\[\begin{array}{l} 1,-432\\ 2,-216\\ \quad\dots \end{array} \nonumber \]

Note that the numbers in the second column are found by dividing \(ac =−432\) by the number in the first column. We’ll now use this fact and the TABLE feature on our calculator to pursue the desired integer pair.

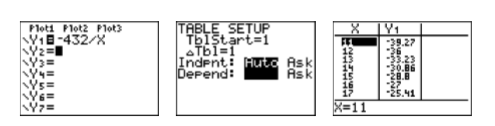
1. Enter the expression \(-432/X\) into \(\mathbb{Y1}\) in the Y= menu (see the first image in Figure \(\PageIndex{1}\)).
2. Above the WINDOW button you’ll see TBLSET. Use the 2nd key, then press the WINDOW button to access the menu shown in the second image of Figure \(\PageIndex{1}\). Set TblStart=1, \(\triangle \text {Tbl}=1\), then highlight AUTO for both the independent and dependent variables.
3. Above the GRAPH button you’ll see TABLE. Use the 2nd key, then press the GRAPH button to access the table shown in the third image in Figure \(\PageIndex{1}\). Use the up- and down-arrow keys to scroll through the contents of the table. Note that you can ignore most of the pairs, because they are not both integers. Pay attention only when they are both integers. In this case, remember that you are searching for a pair whose sum is \(b = −11\). Note that the pair \(16,−27\) shown in the third image of Figure \(\PageIndex{1}\) is the pair we seek.

Figure \(\PageIndex{1}\): Using the TABLE feature to assist the \(ac\)-method.

Now we can break the middle term of \(12y^2 −11y −36\) into a sum of like terms using the ordered pair \(16,−27\), then factor by grouping.

\[\begin{align*} 12y^2-11y-36 &= 12y^2 + 16y-27y-36\\ &= 4y(3y + 4)-9(3y + 4) \\ &= (4y-9)(3y+4) \end{align*} \nonumber \]

Check: Use the FOIL method shortcut and mental calculations to multiply.\[(4y−9)(3y + 4) = 12y^2 −11y−36 \nonumber \]The factorization checks.