6.7: Applications of Factoring

Last updated
Save as PDF

Page ID: 20049

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In this section we will solve applications whose solutions involve factoring. Let’s begin.

Example $\PageIndex{1}$

A rectangular canvas picture measures $12$ inches by $16$ inches. The canvas is mounted inside a frame of uniform width, increasing the total area covered by both canvas and frame to $396$ square inches. Find the uniform width of the frame.

Solution

We follow the Requirements for Word Problem Solutions.

Set up a variable dictionary: A carefully labeled ﬁgure will help us maintain our focus. We’ll let $x$ represent the uniform width of the frame.

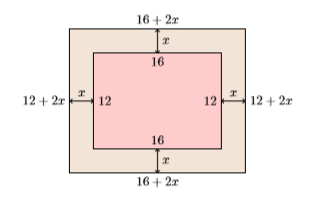
$fig 6.7.1a.png$

Set up an equation: If the inner rectangular dimensions are $16$ inches by $12$ inches, adding a frame of uniform width $x$ makes the dimensions of the frame plus canvas $16 + 2x$ inches by $12 + 2x$ inches. The total area is found by multiplying these outer dimensions, $A = (16 + 2x)(12 + 2x)$. If the total area is $A = 396$ square inches, then we have the following equation.\[(16 + 2x)(12 + 2x) = 396 \nonumber \]
Solve the equation: We start by expanding the right-hand side of the equation.\[\begin{align*} (16 + 2x)(12 + 2x) &= 396\\ 192 + 56x +4x^2 &= 396 \end{align*} \nonumber \]The resulting equation is nonlinear. Make one side zero.\[4x^2 + 56x−204 = 0 \nonumber \]We could factor out $4$ on the left-hand side, but since there is a zero on the right-hand side of the equation, it’s a bit easier to simply divide both sides by $4$. Note how we divide each term on the left-hand side by the number $4$.\[x^2 + 14x−51 = 0 \nonumber \]We need an integer pair whose product is $ac = −51$ and whose sum is $b = 14$. The integer pair $−3,17$ comes to mind. Since the coeﬃcient of $x^2$ is one, we can simply “drop in place” our ordered pair.\[(x−3)(x + 17) = 0 \nonumber \]Thus, the solutions are $x = 3$ and $x = −17$.
Answer the question: The uniform width of the frame cannot be $−17$ inches, so we eliminate this solution from consideration. Hence, the uniform width of the frame is $3$ inches.
Look back: If the uniform width of the frame is $3$ inches, then the ﬁnal dimensions will look like the following.

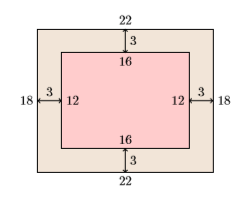
$fig 6.7.1b.png$

Thus, the combined area of the frame plus canvas is $A = (18)(22)$, or $A = 396$ square inches, the area given in the problem statement. Our solution is correct.

Exercise $\PageIndex{1}$

A rectangular canvas picture measures $7$ inches by $11$ inches. The canvas is mounted inside a frame of uniform width, increasing the total area covered by both canvas and frame to $117$ square inches. Find the uniform width of the frame.

Answer: $1$ inch

Example $\PageIndex{2}$

A projectile is ﬁred at an angle into the air from atop a cliﬀ overlooking the ocean. The projectile’s distance (in feet) from the base of the cliﬀ is give by the equation\[x = 120t \label{Eq6.7.1} \]and the projectile’s height above sea level (in feet) is given by the equation\[y = −16t^2 + 288t + 640 \label{Eq6.7.2} \]where $t$ is the amount of time (in seconds) that has passed since the projectile’s release.

How much time passes before the projectile splashes into the ocean?
At that time, how far is the projectile from the base of the cliﬀ?

Solution

We follow the Requirements for Word Problem Solutions.

Set up a variable dictionary: The variables are already set up for us.\[\begin{align*} x &= \text {Distance from base of the cliff (in feet).}\\ y &= \text {Height above sea level (in feet).}\\ t &= \text {Time since projectile's release (in seconds).} \end{align*}\nonumber\]
Set up an equation: The equations are already set up (see Equation \ref{Eq6.7.1} and Equation \ref{Eq6.7.2}).
Solve the equation: When the projectile splashes into the ocean, its height above sea level at that moment is $y = 0$ feet. Substitute $0$ for $y$ in Equation \ref{Eq6.7.2} and solve the resulting equation for $t$.\[\begin{align*} y &= -16t^2 + 288t + 640\\ 0 &= -16t^2 + 288t + 640 \end{align*}\nonumber\]We could factor out $−16$, but since the left-hand side of this equation is zero, it’s a bit easier to divide both sides by $−16$. Note how we divide each term on the right-hand side by $−16$.\[0=t^2 −18t−40 \nonumber \]We need a pair of integers so that their product is $ac = −40$ and their sum is $−18$. The integer pair $2$, $−20$ comes to mind. Since the coeﬃcient of $t^2$ is one, we can “drop in place” our integer pair.\[0=( t + 2)( t−20) \nonumber \]Hence, the solutions are $t = −2$ and $t = 20$.
Answer the question: In answering question (a), the solution $t = −2$ seconds makes no sense. Thus, the projectile splashes into the ocean at $t = 20$ seconds. In addressing question (b), to ﬁnd the projectile’s distance from the base of the cliﬀ at this moment, substitute $t = 20$ in Equation \ref{Eq6.7.1}.\[\begin{align*} x &= 120t\\ x &= 120(20)\\ x &= 2400 \end{align*}\nonumber\]Hence, at the moment the projectile splashes into the ocean, it is $2,400$ feet from the base of the cliﬀ.
Look back: The best we can do here is check our solution $t = 20$ in Equation \ref{Eq6.7.2}.\[\begin{align*} y &= -16t^2 + 288t + 640 \\ y &= -16(20)2 + 288(20)+ 640 \\ y &= -6400+ 5760 + 640 \\ y &= 0 \end{align*}\nonumber\]Indeed, at $t = 20$, the projectile does splash into the ocean.

Exercise $\PageIndex{2}$

A projectile’s height (in feet) is given by the equation $y = −16t^2 + 144t + 576$, where time $t$ is measured in seconds. How much time passes before the projectile hits the ground?

Answer: $12$ seconds

Example $\PageIndex{3}$

The product of two consecutive even integers is $728$. Find the integers.

Solution

We follow the Requirements for Word Problem Solutions.

Set up a variable dictionary: Let $k$ represent the ﬁrst even integer. Then $k + 2$ represents the next consecutive even integer.
Set up an equation: The product of the integers is $728$. Hence, we have the following equation. \[k(k + 2) = 728 \nonumber \]
Solve the equation: Expand the left-hand side of the equation.\[k^2 +2k = 728 \nonumber \]The equation is nonlinear. Make one side zero.\[k^2 +2k−728 = 0 \nonumber \]See Using the Calculator to Assist the $ac$-Method. We need an integer pair whose product is $ac = −728$ and whose sum is $b = 2$. Enter $-728/X$ in $\mathrm{Y1}$, then set up the table (see Figure $\PageIndex{1}$).

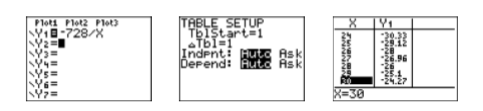
fig 6.7.1.png — Figure $\PageIndex{1}$: Load $ac/X$, or $-728/X$ into $\mathrm{Y1}$ in the **Y= menu**.

Use the up- and down-arrow keys to scroll. Note that $28,−26$ is the desired pair. Because the coeﬃcient of $k^2$ is one, we can “drop in place” the ordered pair.

\[0=( k + 28)(k−26) \nonumber \]Hence, the solutions are $k = −28$ and $k = 26$.

Answer the question: If $k = −28$, the next consecutive even integer is $k +2=−26$. Secondly, if $k = 26$, the next consecutive even integer is $k + 2 = 28$.
Look back: Our ﬁrst pair is $−28$ and $−26$. They have the required product of $728$. Our second pair is $26$ and $28$. Their product is also $728$. Both solutions check!

Exercise $\PageIndex{3}$

The product of two consecutive positive odd integers is $483$. Find the integers.

Answer: $21$ and $23$

Example $\PageIndex{4}$

A rectangle has perimeter $54$ feet and area $180$ square feet. Find the dimensions of the rectangle.

Solution

We follow the Requirements for Word Problem Solutions.

Set up a variable dictionary: A sketch will help us keep our focus. Let $L$ represent the length of the rectangle and let $W$ represent its width.

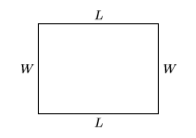
$fig 6.7.2.png$

Set up an equation: The perimeter is $54$ feet, so $2W+2L = 54$, or dividing both sides by $2$:\[W + L = 27 \label{Eq6.7.3} \]The area is $180$ square feet, so:\[LW = 180 \label{Eq6.7.4}\]
Solve the equation: The system of equations (equations \ref{Eq6.7.3} and \ref{Eq6.7.4}) can be solved using the substitution method. First, solve Equation \ref{Eq6.7.3} for $W$:\[W = 27−L \label{Eq6.7.5}\] Substitute Equation \ref{Eq6.7.5} in Equation \ref{Eq6.7.4}, expand, then make one side zero.\[\begin{align*} L(27-L) &= 180 \\ 27L-L^2 &= 180 \\ 0 &= L^2-27L+180 \end{align*}\nonumber\]The integer pair $−12,−15$ has product $ac = 180$ and sum $b = −27$. Moreover, the coeﬃcient of $L^2$ is one, so we can “drop in place” our integer pair.\[0=(L−12)(L−15) \nonumber \] Hence, the solutions are $L = 12$ and $L = 15$.
Answer the question: Two possibilities for the width.
1. Substitute $L = 12$ in \ref{Eq6.7.5}.\[\begin{align*} W &= 27-L \\ W &= 27-12 \\ W &= 15 \end{align*}\nonumber\]
2. Substitute $L = 15$ in \ref{Eq6.7.5}.\[\begin{align*} W &= 27-L \\ W &= 27-15 \\ W &= 12 \end{align*}\nonumber\]

Both answers give the same $15$ by $12$ foot rectangle, but we usually think of the term “length” as the longer side of the rectangle.

So let’s go with the length is $L = 15$ feet and the width is $W = 12$ feet.

Look back: Let’s add $L = 15$ feet and $W = 12$ feet to a diagram.

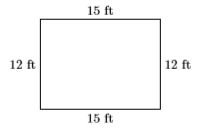
$fig 6.7.3.png$

If we add the dimensions around the rectangle, the perimeter is $P = 15+12 +15+ 12$, or $P = 54$ feet, the perimeter required in the problem statement.

Next, if we multiply the dimensions, then $A = (15)(12)$, or $A = 180$ square feet, the area required in the problem statement. Our solution is correct!

Exercise $\PageIndex{4}$

A rectangle has perimeter $62$ feet and area $234$ square feet. Find the dimensions of the rectangle.

Answer: length = $18$ feet and width = $13$ feet

Search

Text Color

Text Size

Margin Size

Font Type