6.E: Factoring (Exercises)

Last updated

Feb 21, 2022
Save as PDF
- 6.7: Applications of Factoring
- 7: Rational Expressions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

6.1: The Greatest Common Factor

In Exercises 1-6, list all positive divisors of the given number, in order, from smallest to largest.

1) $42$

Answer: $\{1,2,3,6,7,14,21,42\}$

2) $60$

3) $44$

Answer: $\{1,2,4,11,22,44\}$

4) $85$

5) $51$

Answer: $\{1,3,17,51\}$

6) $63$

In Exercises 7-12, list all common positive divisors of the given numbers, in order, from smallest to largest.

7) $36$ and $42$

Answer: $\{1,2,3,6\}$

8) $54$ and $30$

9) $78$ and $54$

Answer: $\{1,2,3,6\}$

10) $96$ and $78$

11) $8$ and $76$

Answer: $\{1,2,4\}$

12) $99$ and $27$

In Exercises 13-18, state the greatest common divisor of the given numbers.

13) $76$ and $8$

Answer: $4$

14) $84$ and $60$

15) $32$ and $36$

Answer: $4$

16) $64$ and $76$

17) $24$ and $28$

Answer: $4$

18) $63$ and $27$

In Exercises 19-24, use prime factorization to help calculate the greatest common divisor of the given numbers.

19) $600$ and $1080$

Answer: $120$

20) $150$ and $120$

21) $1800$ and $2250$

Answer: $450$

22) $540$ and $150$

23) $600$ and $450$

Answer: $150$

24) $4500$ and $1800$

In Exercises 25-36, ﬁnd the greatest common factor of the given expressions.

25) $16b^{4}$ and $56b^{9}$

Answer: $8b^{4}$

26) $28s^{2}$ and $36s^{4}$

27) $35z^{2}$ and $49z^{7}$

Answer: $7z^{2}$

28) $24w^{3}$ and $30w^{8}$

29) $56x^{3} y^{4}$ and $16x^{2} y^{5}$

Answer: $8 x^{2} y^{4}$

30) $35b^{5} c^{3}$ and $63b^{4} c^{4}$

31) $24s^{4} t^{5}$ and $16s^{3} t^{6}$

Answer: $8 s^{3} t^{5}$

32) $10v^{4} w^{3}$ and $8v^{3} w^{4}$

33) $18 y^{7}$ , $45 y^{6}$ , and $27y^{5}$

Answer: $9 y^{5}$

34) $8 r^{7}$ , $24 r^{6}$ , and $12r^{5}$

35) $9 a^{6}$ , $6 a^{5}$ , and $15a^{4}$

Answer: $3 a^{4}$

36) $15 a^{5}$ , $24 a^{4}$ , and $24a^{3}$

In Exercises 37-52, factor out the $\mathrm{GCF}$ from each of the given expressions.

37) $25 a^{2}+10 a+20$

Answer: $5\left(5 a^{2}+2 a+4\right)$

38) $40 c^{2}+15 c+40$

39) $35 s^{2}+25 s+45$

Answer: $5\left(7 s^{2}+5 s+9\right)$

40) $45 b^{2}+20 b+35$

41) $16 c^{3}+32 c^{2}+36 c$

Answer: $4 c\left(4 c^{2}+8 c+9\right)$

42) $12 b^{3}+12 b^{2}+18 b$

43) $42 s^{3}+24 s^{2}+18 s$

Answer: $6 s\left(7 s^{2}+4 s+3\right)$

44) $36 y^{3}+81 y^{2}+36 y$

45) $35 s^{7}+49 s^{6}+63 s^{5}$

Answer: $7 s^{5}\left(5 s^{2}+7 s+9\right)$

46) $35 s^{7}+56 s^{6}+56 s^{5}$

47) $14 b^{7}+35 b^{6}+56 b^{5}$

Answer: $7 b^{5}\left(2 b^{2}+5 b+8\right)$

48) $45 x^{5}+81 x^{4}+45 x^{3}$

49) $54 y^{5} z^{3}+30 y^{4} z^{4}+36 y^{3} z^{5}$

Answer: $6 y^{3} z^{3}\left(9 y^{2}+5 y z+6 z^{2}\right)$

50) $42 x^{4} y^{2}+42 x^{3} y^{3}+54 x^{2} y^{4}$

51) $45 s^{4} t^{3}+40 s^{3} t^{4}+15 s^{2} t^{5}$

Answer: $5.8^{2} t^{3}\left(9 s^{2}+8 s t+3 t^{2}\right)$

52) $20 v^{6} w^{3}+36 v^{5} w^{4}+28 v^{4} w^{5}$

In Exercises 53-60, factor out the $\mathrm{GCF}$ from each of the given expressions.

53) $7 w(2 w-3)-8(2 w-3)$

Answer: $(7 w-8)(2 w-3)$

54) $5 s(8 s-1)+4(8 s-1)$

55) $9 r(5 r-1)+8(5 r-1)$

Answer: $(9 r+8)(5 r-1)$

56) $5 c(4 c-7)+2(4 c-7)$

57) $48 a(2 a+5)-42(2 a+5)$

Answer: $6(2 a+5)(8 a-7)$

58) $40 v(7 v-4)+72(7 v-4)$

59) $56 a(2 a-1)-21(2 a-1)$

Answer: $7(2 a-1)(8 a-3)$

60) $48 r(5 r+3)-40(5 r+3)$

In Exercises 61-68, factor by grouping. Do not simplify the expression before factoring.

61) $x^{2}+2 x-9 x-18$

Answer: $(x-9)(x+2)$

62) $x^{2}+6 x-9 x-54$

63) $x^{2}+3 x+6 x+18$

Answer: $(x+6)(x+3)$

64) $x^{2}+8 x+7 x+56$

65) $x^{2}-6 x-3 x+18$

Answer: $(x-3)(x-6)$

66) $x^{2}-3 x-9 x+27$

67) $x^{2}-9 x+3 x-27$

Answer: $(x+3)(x-9)$

68) $x^{2}-2 x+7 x-14$

In Exercises 69-76, factor by grouping. Do not simplify the expression before factoring.

69) $8 x^{2}+3 x-56 x-21$

Answer: $(x-7)(8 x+3)$

70) $4 x^{2}+9 x-32 x-72$

71) $9 x^{2}+36 x-5 x-20$

Answer: $(9 x-5)(x+4)$

72) $7 x^{2}+14 x-8 x-16$

73) $6 x^{2}-7 x-48 x+56$

Answer: $(x-8)(6 x-7)$

74) $8 x^{2}-7 x-72 x+63$

75) $2 x^{2}+12 x+7 x+42$

Answer: $(2 x+7)(x+6)$

76) $7 x^{2}+28 x+9 x+36$

6.2: Solving Nonlinear Equations

In Exercises 1-8, solve the given equation for $x$ .

1) $(9 x+2)(8 x+3)=0$

Answer: $x=-\dfrac{2}{9},-\dfrac{3}{8}$

2) $(2 x-5)(7 x-4)=0$

3) $x(4 x+7)(9 x-8)=0$

Answer: $x=0,-\dfrac{7}{4}, \dfrac{8}{9}$

4) $x(9 x-8)(3 x+1)=0$

5) $-9 x(9 x+4)=0$

Answer: $x=0,-\dfrac{4}{9}$

6) $4 x(3 x-6)=0$

7) $(x+1)(x+6)=0$

Answer: $x=-1,-6$

8) $(x-4)(x-1)=0$

In Exercises 9-18, given that you are solving for $x$ , state whether the given equation is linear or nonlinear. Do not solve the equation.

9) $x^{2}+7 x=9 x+63$

Answer: Nonlinear

10) $x^{2}+9 x=4 x+36$

11) $6 x-2=5 x-8$

Answer: Linear

12) $-5 x+5=-6 x-7$

13) $7 x^{2}=-2 x$

Answer: Nonlinear

14) $4 x^{2}=-7 x$

15) $3 x^{2}+8 x=-9$

Answer: Nonlinear

16) $5 x^{2}-2 x=-9$

17) $-3 x+6=-9$

Answer: Linear

18) $8 x-5=3$

In Exercises 19-34, solve each of the given equations for $x$ .

19) $3 x+8=9$

Answer: $\dfrac{1}{3}$

20) $3 x+4=2$

21) $9 x^{2}=-x$

Answer: $x=0,-\dfrac{1}{9}$

22) $6 x^{2}=7 x$

23) $3 x+9=8 x+7$

Answer: $\dfrac{2}{5}$

24) $8 x+5=6 x+4$

25) $8 x^{2}=-2 x$

Answer: $x=0,-\dfrac{1}{4}$

26) $8 x^{2}=18 x$

27) $9 x+2=7$

Answer: $\dfrac{5}{9}$

28) $3 x+2=6$

29) $9 x^{2}=6 x$

Answer: $x=0, \dfrac{2}{3}$

30) $6 x^{2}=-14 x$

31) $7 x^{2}=-4 x$

Answer: $x=0,-\dfrac{4}{7}$

32) $7 x^{2}=-9 x$

33) $7 x+2=4 x+7$

Answer: $\dfrac{5}{3}$

34) $4 x+3=2 x+8$

In Exercises 35-50, factor by grouping to solve each of the given equations for $x$ .

35) $63 x^{2}+56 x+54 x+48=0$

Answer: $x=-\dfrac{6}{7},-\dfrac{8}{9}$

36) $27 x^{2}+36 x+6 x+8=0$

37) $16 x^{2}-18 x+40 x-45=0$

Answer: $x=-\dfrac{5}{2}, \dfrac{9}{8}$

38) $42 x^{2}-35 x+54 x-45=0$

39) $45 x^{2}+18 x+20 x+8=0$

Answer: $x=-\dfrac{4}{9},-\dfrac{2}{5}$

40) $18 x^{2}+21 x+30 x+35=0$

41) $x^{2}+10 x+4 x+40=0$

Answer: $x=-4,-10$

42) $x^{2}+11 x+10 x+110=0$

43) $x^{2}+6 x-11 x-66=0$

Answer: $x=11,-6$

44) $x^{2}+6 x-2 x-12=0$

45) $15 x^{2}-24 x+35 x-56=0$

Answer: $x=-\dfrac{7}{3}, \dfrac{8}{5}$

46) $12 x^{2}-10 x+54 x-45=0$

47) $x^{2}+2 x+9 x+18=0$

Answer: $x=-9,-2$

48) $x^{2}+8 x+4 x+32=0$

49) $x^{2}+4 x-8 x-32=0$

Answer: $x=8,-4$

50) $x^{2}+8 x-5 x-40=0$

In Exercises 51-54, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 5:intersect utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.2.7.

51) $x^{2}=-4 x$

Answer: $x=-4,0$

52) $x^{2}=6 x$

53) $x^{2}=5 x$

Answer: $x=0,5$

54) $x^{2}=-6 x$

In Exercises 55-58, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 2:zero utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.2.8.

55) $x^{2}+7 x=0$

Answer: $x=-7,0$

56) $x^{2}-8 x=0$

57) $x^{2}-3 x=0$

Answer: $x=0,3$

58) $x^{2}+2 x=0$

6.3: Factoring ax² + bx + c when a =1

In Exercises 1-6, compare the given trinomial with $ax^2 + bx + c$ , then list ALL integer pairs whose product equals $ac$ . Circle the pair whose sum equals $b$ , then use this pair to help factor the given trinomial.

1) $x^{2}+7 x-18$

Answer: $(x-2)(x+9)$

2) $x^{2}+18 x+80$

3) $x^{2}-10 x+9$

Answer: $(x-1)(x-9)$

4) $x^{2}+12 x+27$

5) $x^{2}+14 x+45$

Answer: $(x+5)(x+9)$

6) $x^{2}+9 x+20$

In Exercises 7-12, compare the given trinomial with $ax^2 +bx+c$ , then begin listing integer pairs whose product equals $ac$ . Cease the list process when you discover a pair whose sum equals $b$ , then circle and use this pair to help factor the given trinomial.

7) $x^{2}-16 x+39$

Answer: $(x-3)(x-13)$

8) $x^{2}-16 x+48$

9) $x^{2}-26 x+69$

Answer: $(x-3)(x-23)$

10) $x^{2}-22 x+57$

11) $x^{2}-25 x+84$

Answer: $(x-4)(x-21)$

12) $x^{2}+13 x-30$

In Exercises 13-18, compare the given trinomial with $ax^2 + bx + c$ , then compute $ac$ . Try to mentally discover the integer pair whose product is $ac$ and whose sum is $b$ . Factor the trinomial by “dropping this pair in place.”

Note: If you ﬁnd you cannot identify the pair mentally, begin listing integer pairs whose product equals $ac$ , then cease the listing process when you encounter the pair whose sum equals $b$ .

13) $x^{2}-13 x+36$

Answer: $(x-4)(x-9)$

14) $x^{2}+x-12$

15) $x^{2}+10 x+21$

Answer: $(x+3)(x+7)$

16) $x^{2}-17 x+66$

17) $x^{2}-4 x-5$

Answer: $(x+1)(x-5)$

18) $x^{2}-20 x+99$

In Exercises 19-24, use an algebraic technique to solve the given equation.

19) $x^{2}=-7 x+30$

Answer: $x=3,-10$

20) $x^{2}=-2 x+35$

21) $x^{2}=-11 x-10$

Answer: $x=-1,-10$

22) $x^{2}=x+72$

23) $x^{2}=-15 x-50$

Answer: $x=-5,-10$

24) $x^{2}=-7 x-6$

In Exercises 25-30, use an algebraic technique to solve the given equation.

25) $60=x^{2}+11 x$

Answer: $x=4,-15$

26) $-92=x^{2}-27 x$

27) $-11=x^{2}-12 x$

Answer: $x=1,11$

28) $80=x^{2}-16 x$

29) $56=x^{2}+10 x$

Answer: $x=4,-14$

30) $66=x^{2}+19 x$

In Exercises 31-36, use an algebraic technique to solve the given equation.

31) $x^{2}+20=-12 x$

Answer: $x=-2,-10$

32) $x^{2}-12=11 x$

33) $x^{2}-36=9 x$

Answer: $x=-3,12$

34) $x^{2}+6=5 x$

35) $x^{2}+8=-6 x$

Answer: $x=-2,-4$

36) $x^{2}+77=18 x$

In Exercises 37-40, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 5:intersect utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.3.6.

37) $x^{2}=x+12$

Answer: $x=-3,4$

38) $x^{2}=20-x$

39) $x^{2}+12=8 x$

Answer: $x=2,6$

40) $x^{2}+7=8 x$

In Exercises 41-44, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 2:zero utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.3.7.

41) $x^{2}-6 x-16=0$

Answer: $x=8,-2$

42) $x^{2}+7 x-18=0$

43) $x^{2}+10 x-24=0$

Answer: $x=-12,2$

44) $x^{2}-9 x-36=0$

6.4: Factoring ax² + bx + c when a≠1

1) $6 x^{2}+13 x-5$

Answer: $(2 x+5)(3 x-1)$

2) $3 x^{2}-19 x+20$

3) $4 x^{2}-x-3$

Answer: $(x-1)(4 x+3)$

4) $6 x^{2}-23 x+7$

5) $3 x^{2}+19 x+28$

Answer: $(x+4)(3 x+7)$

6) $2 x^{2}-9 x-18$

7) $12 x^{2}-23 x+5$

Answer: $(3 x-5)(4 x-1)$

8) $8 x^{2}+22 x+9$

9) $6 x^{2}+17 x+7$

Answer: $(2 x+1)(3 x+7)$

10) $4 x^{2}+19 x+21$

11) $3 x^{2}+4 x-32$

Answer: $(x+4)(3 x-8)$

12) $4 x^{2}+x-14$

In Exercises 13-18, compare the given trinomial with $ax^2 + bx + c$ , then compute $ac$ . Try to mentally discover the integer pair whose product is $ac$ and whose sum is $b$ . Use this pair to help factor the given trinomial.

Note: If you ﬁnd you cannot identify the pair mentally, begin listing integer pairs whose product equals $ac$ , then cease the listing process when you encounter the pair whose sum equals $b$ .

13) $3 x^{2}+28 x+9$

Answer: $(3 x+1)(x+9)$

14) $6 x^{2}+x-1$

15) $4 x^{2}-21 x+5$

Answer: $(x-5)(4 x-1)$

16) $4 x^{2}-x-14$

17) $6 x^{2}-11 x-7$

Answer: $(3 x-7)(2 x+1)$

18) $2 x^{2}-17 x+21$

In Exercises 19-26, factor the trinomial.

19) $16 x^{5}-36 x^{4}+14 x^{3}$

Answer: $2 x^{3}(2 x-1)(4 x-7)$

20) $12 x^{4}-20 x^{3}+8 x^{2}$

21) $36 x^{4}-75 x^{3}+21 x^{2}$

Answer: $3 x^{2}(3 x-1)(4 x-7)$

22) $6 x^{4}-10 x^{3}-24 x^{2}$

23) $6 x^{4}-33 x^{3}+42 x^{2}$

Answer: $3 x^{2}(x-2)(2 x-7)$

24) $15 x^{3}-10 x^{2}-105 x$

25) $16 x^{4}-36 x^{3}-36 x^{2}$

Answer: $4 x^{2}(x-3)(4 x+3)$

26) $40 x^{4}-10 x^{3}-5 x^{2}$

In Exercises 27-38, use an algebraic technique to solve the given equation.

27) $(10-8)^{2}-(7-5)^{3}$

Answer: $x=2,-\dfrac{9}{4}$

28) $2 x^{2}=7 x-3$

29) $3 x^{2}+16=-14 x$

Answer: $x=-2,-\dfrac{8}{3}$

30) $2 x^{2}-20=-3 x$

31) $3 x^{2}+30=23 x$

Answer: $x=6, \dfrac{5}{3}$

32) $6 x^{2}-7=-11 x$

33) $-7 x-3=-6 x^{2}$

Answer: $x=-\dfrac{1}{3}, \dfrac{3}{2}$

34) $13 x-45=-2 x^{2}$

35) $26 x-9=-3 x^{2}$

Answer: $x=-9, \dfrac{1}{3}$

36) $-23 x+7=-6 x^{2}$

37) $6 x^{2}=-25 x+9$

Answer: $x=\dfrac{1}{3},-\dfrac{9}{2}$

38) $2 x^{2}=13 x+45$

In Exercises 39-42, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 2:zero utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.4.5.

39) $2 x^{2}-9 x-5=0$

Answer: $x=-\dfrac{1}{2},5$

40) $2 x^{2}+x-28=0$

41) $4 x^{2}-17 x-15=0$

Answer: $x=-\dfrac{3}{4},5$

42) $3 x^{2}+14 x-24=0$

In Exercises 43-46, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 2:zero utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.4.6.

43) $2 x^{3}=3 x^{2}+20 x$

Answer: $x=0,-\dfrac{5}{2},4$

44) $2 x^{3}=3 x^{2}+35 x$

45) $10 x^{3}+34 x^{2}=24 x$

Answer: $x=0,-4, \dfrac{3}{5}$

46) $6 x^{3}+3 x^{2}=63 x$

6.5: Factoring Special Forms

In Exercises 1-8, expand each of the given expressions.

1) $(8 r-3 t)^{2}$

Answer: $64 r^{2}-48 r t+9 t^{2}$

2) $(6 a+c)^{2}$

3) $(4 a+7 b)^{2}$

Answer: $16 a^{2}+56 a b+49 b^{2}$

4) $(4 s+t)^{2}$

5) $\left(s^{3}-9\right)^{2}$

Answer: $s^{6}-18 s^{3}+81$

6) $\left(w^{3}+7\right)^{2}$

7) $\left(s^{2}+6 t^{2}\right)^{2}$

Answer: $s^{4}+12 s^{2} t^{2}+36 t^{4}$

8) $\left(7 u^{2}-2 w^{2}\right)^{2}$

In Exercises 9-28, factor each of the given expressions.

9) $25 s^{2}+60 s t+36 t^{2}$

Answer: $(5 s+6 t)^{2}$

10) $9 u^{2}+24 u v+16 v^{2}$

11) $36 v^{2}-60 v w+25 w^{2}$

Answer: $(6 v-5 w)^{2}$

12) $49 b^{2}-42 b c+9 c^{2}$

13) $a^{4}+18 a^{2} b^{2}+81 b^{4}$

Answer: $\left(a^{2}+9 b^{2}\right)^{2}$

14) $64 u^{4}-144 u^{2} w^{2}+81 w^{4}$

15) $49 s^{4}-28 s^{2} t^{2}+4 t^{4}$

Answer: $\left(7 s^{2}-2 t^{2}\right)^{2}$

16) $4 a^{4}-12 a^{2} c^{2}+9 c^{4}$

17) $49 b^{6}-112 b^{3}+64$

Answer: $\left(7 b^{3}-8\right)^{2}$

18) $25 x^{6}-10 x^{3}+1$

19) $49 r^{6}+112 r^{3}+64$

Answer: $\left(7 r^{3}+8\right)^{2}$

20) $a^{6}-16 a^{3}+64$

21) $5 s^{3} t-20 s^{2} t^{2}+20 s t^{3}$

Answer: $5 s t(s-2 t)^{2}$

22) $12 r^{3} t-12 r^{2} t^{2}+3 r t^{3}$

23) $8 a^{3} c+8 a^{2} c^{2}+2 a c^{3}$

Answer: $2 a c(2 a+c)^{2}$

24) $18 x^{3} z-60 x^{2} z^{2}+50 x z^{3}$

25) $-48 b^{3}+120 b^{2}-75 b$

Answer: $-3 b(4 b-5)^{2}$

26) $-45 c^{3}+120 c^{2}-80 c$

27) $-5 u^{5}-30 u^{4}-45 u^{3}$

Answer: $-5 u^{3}(u+3)^{2}$

28) $-12 z^{5}-36 z^{4}-27 z^{3}$

In Exercises 29-36, expand each of the given expressions.

29) $(21 c+16)(21 c-16)$

Answer: $441 c^{2}-256$

30) $(19 t+7)(19 t-7)$

31) $(5 x+19 z)(5 x-19 z)$

Answer: $25 x^{2}-361 z^{2}$

32) $(11 u+5 w)(11 u-5 w)$

33) $\left(3 y^{4}+23 z^{4}\right)\left(3 y^{4}-23 z^{4}\right)$

Answer: $9 y^{8}-529 z^{8}$

34) $\left(5 x^{3}+z^{3}\right)\left(5 x^{3}-z^{3}\right)$

35) $\left(8 r^{5}+19 s^{5}\right)\left(8 r^{5}-19 s^{5}\right)$

Answer: $64 r^{10}-361 s^{10}$

36) $\left(3 u^{3}+16 v^{3}\right)\left(3 u^{3}-16 v^{3}\right)$

In Exercises 37-60, factor each of the given expressions.

37) $361 x^{2}-529$

Answer: $(19 x+23)(19 x-23)$

38) $9 b^{2}-25$

39) $16 v^{2}-169$

Answer: $(4 v+13)(4 v-13)$

40) $81 r^{2}-169$

41) $169 x^{2}-576 y^{2}$

Answer: $(13 x+24 y)(13 x-24 y)$

42) $100 y^{2}-81 z^{2}$

43) $529 r^{2}-289 s^{2}$

Answer: $(23 r+17 s)(23 r-17 s)$

44) $49 a^{2}-144 b^{2}$

45) $49 r^{6}-256 t^{6}$

Answer: $\left(7 r^{3}+16 t^{3}\right)\left(7 r^{3}-16 t^{3}\right)$

46) $361 x^{10}-484 z^{10}$

47) $36 u^{10}-25 w^{10}$

Answer: $\left(6 u^{5}+5 w^{5}\right)\left(6 u^{5}-5 w^{5}\right)$

48) $a^{6}-81 c^{6}$

49) $72 y^{5}-242 y^{3}$

Answer: $2 y^{3}(6 y+11)(6 y-11)$

50) $75 y^{5}-147 y^{3}$

51) $1444 a^{3} b-324 a b^{3}$

Answer: $4 a b(19 a+9 b)(19 a-9 b)$

52) $12 b^{3} c-1875 b c^{3}$

53) $576 x^{3} z-1156 x z^{3}$

Answer: $4 x z(12 x+17 z)(12 x-17 z)$

54) $192 u^{3} v-507 u v^{3}$

55) $576 t^{4}-4 t^{2}$

Answer: $4 t^{2}(12 t+1)(12 t-1)$

56) $4 z^{5}-256 z^{3}$

57) $81 x^{4}-256$

Answer: $\left(9 x^{2}+16\right)(3 x+4)(3 x-4)$

58) $81 x^{4}-1$

59) $81 x^{4}-16$

Answer: $\left(9 x^{2}+4\right)(3 x+2)(3 x-2)$

60) $x^{4}-1$

In Exercises 61-68, factor each of the given expressions completely.

61) $z^{3}+z^{2}-9 z-9$

Answer: $(z+3)(z-3)(z+1)$

62) $3 u^{3}+u^{2}-48 u-16$

63) $x^{3}-2 x^{2} y-x y^{2}+2 y^{3}$

Answer: $(x+y)(x-y)(x-2 y)$

64) $x^{3}+2 x^{2} z-4 x z^{2}-8 z^{3}$

65) $r^{3}-3 r^{2} t-25 r t^{2}+75 t^{3}$

Answer: $(r+5 t)(r-5 t)(r-3 t)$

66) $2 b^{3}-3 b^{2} c-50 b c^{2}+75 c^{3}$

67) $2 x^{3}+x^{2}-32 x-16$

Answer: $(x+4)(x-4)(2 x+1)$

68) $r^{3}-2 r^{2}-r+2$

In Exercises 69-80, solve each of the given equations for $x$ .

69) $2 x^{3}+7 x^{2}=72 x+252$

Answer: $x=-6,6,-\dfrac{7}{2}$

70) $2 x^{3}+7 x^{2}=32 x+112$

71) $x^{3}+5 x^{2}=64 x+320$

Answer: $x=-8,8,-5$

72) $x^{3}+4 x^{2}=49 x+196$

73) $144 x^{2}+121=264 x$

Answer: $x=\dfrac{11}{12}$

74) $361 x^{2}+529=874 x$

75) $16 x^{2}=169$

Answer: $x=-\dfrac{13}{4}, \dfrac{13}{4}$

76) $289 x^{2}=4$

77) $9 x^{2}=25$

Answer: $x=-\dfrac{5}{3}, \dfrac{5}{3}$

78) $144 x^{2}=121$

79) $256 x^{2}+361=-608 x$

Answer: $x=-\dfrac{19}{16}$

80) $16 x^{2}+289=-136 x$

In Exercises 81-84, perform each of the following tasks:

Use a strictly algebraic technique to solve the given equation.
Use the 5:intersect utility on your graphing calculator to solve the given equation.

Report the results found using graphing calculator as shown in Example 6.5.12.

81) $x^{3}=x$

Answer: $x=0,-1,1$

82) $x^{3}=9 x$

83) $4 x^{3}=x$

Answer: $x=0,-\dfrac{1}{2},\dfrac{1}{2}$

84) $9 x^{3}=x$

6.6: Factoring Strategy

In Exercises 1-12, factor each of the given polynomials completely.

1) $484 y^{4} z^{2}-144 y^{2} z^{4}$

Answer: $4 y^{2} z^{2}(11 y+6 z)(11 y-6 z)$

2) $72 s^{4} t^{4}-242 s^{2} t^{6}$

3) $3 x^{7} z^{5}-363 x^{5} z^{5}$

Answer: $3 x^{5} z^{5}(x+11)(x-11)$

4) $5 r^{5} s^{2}-80 r^{3} s^{2}$

5) $2 u^{7}-162 u^{5}$

Answer: $2u^5(u + 9)(u−9)$

6) $405 x^{4}-320 x^{2}$

7) $3 v^{8}-1875 v^{4}$

Answer: $3v^4(v^2 + 25)(v + 5)(v−5)$

8) $3 a^{9}-48 a^{5}$

9) $3 x^{6}-300 x^{4}$

Answer: $3 x^{4}(x+10)(x-10)$

10) $2 y^{5}-18 y^{3}$

11) $1250 u^{7} w^{3}-2 u^{3} w^{7}$

Answer: $2 u^{3} w^{3}\left(25 u^{2}+w^{2}\right)(5 u+w)(5 u-w)$

12) $48 y^{8} z^{4}-3 y^{4} z^{8}$

In Exercises 13-24, factor each of the given polynomials completely.

13) $75 a^{6}-210 a^{5}+147 a^{4}$

Answer: $3 a^{4}(5 a-7)^{2}$

14) $245 v^{7}-560 v^{6}+320 v^{5}$

15) $180 a^{5} b^{3}+540 a^{4} b^{4}+405 a^{3} b^{5}$

Answer: $45 a^{3} b^{3}(2 a+3 b)^{2}$

16) $192 u^{6} v^{4}+432 u^{5} v^{5}+243 u^{4} v^{6}$

17) $2 b^{5}+4 b^{4}+2 b^{3}$

Answer: $2 b^{3}(b+1)^{2}$

18) $3 v^{6}+30 v^{5}+75 v^{4}$

19) $2 z^{4}-4 z^{3}+2 z^{2}$

Answer: $2 z^{2}(z-1)^{2}$

20) $2 u^{6}-40 u^{5}+200 u^{4}$

21) $324 x^{4}+360 x^{3}+100 x^{2}$

Answer: $4 x^{2}(9 x+5)^{2}$

22) $98 b^{4}+84 b^{3}+18 b^{2}$

23) $75 b^{4} c^{5}-240 b^{3} c^{6}+192 b^{2} c^{7}$

Answer: $3 b^{2} c^{5}(5 b-8 c)^{2}$

24) $162 a^{5} c^{4}-180 a^{4} c^{5}+50 a^{3} c^{6}$

In Exercises 25-36, factor each of the given polynomials completely.

25) $5 a^{5}+5 a^{4}-210 a^{3}$

Answer: $5 a^{3}(a-6)(a+7)$

26) $3 y^{5}-9 y^{4}-12 y^{3}$

27) $3 y^{6}-39 y^{5}+120 y^{4}$

Answer: $3 y^{4}(y-8)(y-5)$

28) $3 y^{7}-27 y^{6}+42 y^{5}$

29) $3 z^{4}+12 z^{3}-135 z^{2}$

Answer: $3 z^{2}(z-5)(z+9)$

30) $5 a^{4}-40 a^{3}-45 a^{2}$

31) $4 a^{6}+64 a^{5}+252 a^{4}$

Answer: $4 a^{4}(a+9)(a+7)$

32) $4 x^{4}+64 x^{3}+252 x^{2}$

33) $3 z^{4}+33 z^{3}+84 z^{2}$

Answer: $3 z^{2}(z+7)(z+4)$

34) $5 a^{6}+65 a^{5}+180 a^{4}$

35) $5 z^{7}-75 z^{6}+270 z^{5}$

Answer: $5 z^{5}(z-6)(z-9)$

36) $3 y^{4}-27 y^{3}+24 y^{2}$

In Exercises 37-48, factor each of the given polynomials completely.

37) $4 b^{3}-22 b^{2}+30 b$

Answer: $2 b(2 b-5)(b-3)$

38) $4 b^{6}-22 b^{5}+30 b^{4}$

39) $2 u^{4} w^{5}-3 u^{3} w^{6}-20 u^{2} w^{7}$

Answer: $u^{2} w^{5}(u-4 w)(2 u+5 w)$

40) $12 x^{5} z^{2}+9 x^{4} z^{3}-30 x^{3} z^{4}$

41) $12 x^{4} y^{5}+50 x^{3} y^{6}+50 x^{2} y^{7}$

Answer: $2 x^{2} y^{5}(3 x+5 y)(2 x+5 y)$

42) $24 s^{4} t^{3}+62 s^{3} t^{4}+40 s^{2} t^{5}$

43) $12 x^{3}+9 x^{2}-30 x$

Answer: $3 x(4 x-5)(x+2)$

44) $6 v^{4}+2 v^{3}-20 v^{2}$

45) $8 u^{6}+34 u^{5}+30 u^{4}$

Answer: $2 u^{4}(4 u+5)(u+3)$

46) $4 a^{4}+29 a^{3}+30 a^{2}$

47) $12 a^{4} c^{4}-35 a^{3} c^{5}+25 a^{2} c^{6}$

Answer: $a^{2} c^{A}(4 a-5 c)(3 a-5 c)$

48) $18 x^{6} z^{5}-39 x^{5} z^{6}+18 x^{4} z^{7}$

In Exercises 49-56, factor each of the given polynomials completely.

49) $12 y^{5}+15 y^{4}-108 y^{3}-135 y^{2}$

Answer: $3 y^{2}(y+3)(y-3)(4 y+5)$

50) $9 b^{8}+12 b^{7}-324 b^{6}-432 b^{5}$

51) $9 x^{6} z^{5}+6 x^{5} z^{6}-144 x^{4} z^{7}-96 x^{3} z^{8}$

Answer: $3 x^{3} z^{5}(x+4 z)(x-4 z)(3 x+2 z)$

52) $12 u^{7} w^{3}+9 u^{6} w^{4}-432 u^{5} w^{5}-324 u^{4} w^{6}$

53) $72 z^{6}+108 z^{5}-2 z^{4}-3 z^{3}$

Answer: $z^{3}(6 z+1)(6 z-1)(2 z+3)$

54) $216 x^{7}+324 x^{6}-6 x^{5}-9 x^{4}$

55) $144 a^{6} c^{3}+360 a^{5} c^{4}-4 a^{4} c^{5}-10 a^{3} c^{6}$

Answer: $2 a^{3} c^{3}(6 a+c)(6 a-c)(2 a+5 c)$

56) $48 a^{8} c^{4}+32 a^{7} c^{5}-3 a^{6} c^{6}-2 a^{5} c^{7}$

In Exercises 57-60, use your calculator to help factor each of the given trinomials. Follow the procedure outline in Using the Calculator to Assist the $ac$ -Method.

57) $6 x^{2}+61 x+120$

Answer: $(2 x+15)(3 x+8)$

58) $16 x^{2}-62 x-45$

59) $60 x^{2}-167 x+72$

Answer: $(15 x-8)(4 x-9)$

60) $28 x^{2}+x-144$

6.7: Applications of Factoring

1) A rectangular canvas picture measures $14$ inches by $36$ inches. The canvas is mounted inside a frame of uniform width, increasing the total area covered by both canvas and frame to $720$ square inches. Find the uniform width of the frame.

Answer: $2$ inches

2) A rectangular canvas picture measures $10$ inches by $32$ inches. The canvas is mounted inside a frame of uniform width, increasing the total area covered by both canvas and frame to $504$ square inches. Find the uniform width of the frame.

3) A projectile is ﬁred at an angle into the air from atop a cliﬀ overlooking the ocean. The projectile’s distance (in feet) from the base of the cliﬀ is give by the equation $x = 180t \nonumber$ and the projectile’s height above sea level (in feet) is given by the equation $y = −16t^2 + 352t + 1664 \nonumber$ where $t$ is the amount of time (in seconds) that has passed since the projectile’s release. How much time passes before the projectile splashes into the ocean? At that time, how far is the projectile from the base of the cliﬀ?

Answer: $26$ seconds, $4,680$ feet

4) A projectile is ﬁred at an angle into the air from atop a cliﬀ overlooking the ocean. The projectile’s distance (in feet) from the base of the cliﬀ is give by the equation $x = 140t \nonumber$ and the projectile’s height above sea level (in feet) is given by the equation $y = −16t^2 + 288t + 1408 \nonumber$ where $t$ is the amount of time (in seconds) that has passed since the projectile’s release. How much time passes before the projectile splashes into the ocean? At that time, how far is the projectile from the base of the cliﬀ?

5) The product of two consecutive even integers is $624$ . Find the integers.

Answer: $-26$ and $−24$ , and $24$ and $26$

6) The product of two consecutive even integers is $528$ . Find the integers.

7) The product of two consecutive positive integers is $552$ . Find the integers.

Answer: $23$ , $24$

8) The product of two consecutive positive integers is $756$ . Find the integers.

9) The product of two consecutive odd integers is $483$ . Find the integers.

Answer: $−23$ and $−21$ , and $21$ and $23$

10) The product of two consecutive odd integers is $783$ . Find the integers.

11) A rectangle has perimeter $42$ feet and area $104$ square feet. Find the dimensions of the rectangle.

Answer: $8$ feet by $13$ feet

12) A rectangle has perimeter $32$ feet and area $55$ square feet. Find the dimensions of the rectangle.

13) The radius of the outer circle is one inch longer than twice the radius of the inner circle.

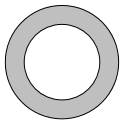
If the area of the shaded region is $40\pi$ square inches, what is the length of the inner radius?

Answer: $3$ inches

14) The radius of the outer circle is two inches longer than three times the radius of the inner circle.

If the area of the shaded region is $180\pi$ square inches, what is the length of the inner radius?

15) You have two positive numbers. The second number is three more than two times the ﬁrst number. The diﬀerence of their squares is $144$ . Find both positive numbers.

Answer: $5$ and $13$

16) You have two positive numbers. The second number is two more than three times the ﬁrst number. The diﬀerence of their squares is $60$ . Find both positive numbers.

17) Two numbers diﬀer by $5$ . The sum of their squares is $97$ . Find the two numbers.

Answer: $4$ and $9$ , and $−4$ and $−9$

18) Two numbers diﬀer by $6$ . The sum of their squares is $146$ . Find the two numbers.

19) The length of a rectangle is three feet longer than six times its width. If the area of the rectangle is $165$ square feet, what is the width of the rectangle?

Answer: $5$ feet

20) The length of a rectangle is three feet longer than nine times its width. If the area of the rectangle is $90$ square feet, what is the width of the rectangle?

21) The ratio of the width to the length of a given rectangle is $2$ to $3$ , or $\dfrac {2}{3}$ . If the width and length are both increased by $4$ inches, the area of the resulting rectangle is $80$ square inches. Find the width and length of the original rectangle.

Answer: $4$ inches by $6$ inches

22) The ratio of the width to the length of a given rectangle is $3$ to $4$ , or $\dfrac {3}{4}$ . If the width is increased by $3$ inches and the length is increased by $6$ inches, the area of the resulting rectangle is $126$ square inches. Find the width and length of the original rectangle.

Search

Text Color

Text Size

Margin Size

Font Type