8.2: Simplifying Radical Expressions

Last updated
Save as PDF

Page ID: 19899

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Let’s begin by comparing two mathematical expressions.

\[\begin{align*} \sqrt{9}\sqrt{16} &= 3\cdot 4 \\ &= 12 \end{align*} \nonumber \]

and

\[\begin{align*} \sqrt{9\cdot 16} &= \sqrt{144} \\ &= 12 \end{align*} \nonumber\]

Note that both $\sqrt{9}\sqrt{16}$ and $\sqrt{9\cdot 16}$ equal $12$. Hence, $\sqrt{9}\sqrt{16} = \sqrt{9\cdot 16}$. Let’s look at another example.

\[\begin{align*} \sqrt{4}\sqrt{9} &= 2\cdot 3 \\ &= 6 \end{align*} \nonumber \]

and

\[\begin{align*} \sqrt{4\cdot 9} &= \sqrt{36} \\ &= 6 \end{align*} \nonumber\]

Note that both $\sqrt{4}\sqrt{9}$ and $\sqrt{4\cdot 9}$ equal $6$. Hence, $\sqrt{4}\sqrt{9} = \sqrt{4\cdot 9}$. It appears that a pattern is forming, namely:

\[\sqrt{a}\sqrt{b} = \sqrt{ab} \nonumber \]

Let’s try an example on our calculator. First enter $\sqrt{2}\sqrt{3}$, then enter $\sqrt{2\cdot 3}$ (see Figure $\PageIndex{1}$). Note that they produce the same result. Therefore, $\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

fig 8.2.1.png — Figure $\PageIndex{1}$: Note that $\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

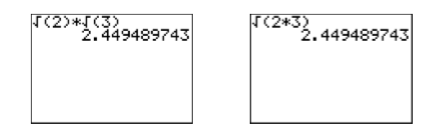
The above discussion leads us to the following result.

Multiplication property of radicals

If $a ≥ 0$ and $b ≥ 0$, then:\[\sqrt{a}\sqrt{b} = \sqrt{a\cdot b} \nonumber \]

Example $\PageIndex{1}$

Simplify each of the following expressions as much as possible:

$\sqrt{3} \sqrt{11}$
$\sqrt{12} \sqrt{3}$
$\sqrt{2} \sqrt{13}$

Solution

In each case, use the property $\sqrt{a} \sqrt{b}=\sqrt{a b}$. That is, multiply the two numbers under the square root sign, placing the product under a single square root.

$\begin{aligned} \sqrt{3} \sqrt{11} &=\sqrt{3 \cdot 11} \\ &=\sqrt{33} \end{aligned}$
$\begin{aligned} \sqrt{12} \sqrt{3} &=\sqrt{12 \cdot 3} \\ &=\sqrt{36} \\ &=6 \end{aligned}$
$\begin{aligned} \sqrt{2} \sqrt{13} &=\sqrt{2 \cdot 13} \\ &=\sqrt{26} \end{aligned}$

Exercise $\PageIndex{1}$

Simplify: $\sqrt{2} \sqrt{8}$

Answer: $4$

Simple Radical Form

We can also use the property $\sqrt{a} \sqrt{b}=\sqrt{a b}$ in reverse to factor out a perfect square. For example:

\[\begin{array}{rlrl}{\sqrt{50}} & {=\sqrt{25} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=5 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{25}=5}\end{array} \nonumber \]

The expression $5\sqrt{2}$ is said to be in simple radical form. Like reducing a fraction to lowest terms, you should always look to factor out a perfect square when possible.

Simple Radical Form

If possible, always factor out a perfect square.

Example $\PageIndex{2}$

Place $\sqrt{8}$ in simple radical form.

Solution

From $\sqrt{8}$, we can factor out a perfect square, in this case $\sqrt{4}$.

\[\begin{array}{rlrl}{\sqrt{8}} & {=\sqrt{4} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=2 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber \]

Exercise $\PageIndex{2}$

Place $\sqrt{12}$ in simple radical form.

Answer: $2\sqrt{3}$

Sometimes, after factoring out a perfect square, you can still factor out another perfect square.

Example $\PageIndex{3}$

Place $\sqrt{72}$ in simple radical form.

Solution

From $\sqrt{72}$, we can factor out a perfect square, in this case $\sqrt{9}$.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{9} \sqrt{8}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=3 \sqrt{8}} & {} & \color {Red} {\text { Simplify: } \sqrt{9}=3}\end{array} \nonumber \]

However, from $\sqrt{8}$ we can factor out another perfect square, in this case $\sqrt{4}$.

\[\begin{array}{ll}{=3 \sqrt{4} \sqrt{2}} & \color {Red} {\text { Factor out another perfect square. }} \\ {=3 \cdot 2 \cdot \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {=6 \sqrt{2}} & \color {Red} {\text { Multiply: } 3 \cdot 2=6}\end{array} \nonumber \]

Alternate solution

We can simplify the process by noting that we can factor out $\sqrt{36}$ from $\sqrt{72}$ to start the process.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{36} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=6 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Although the second solution is more eﬃcient, the ﬁrst solution is still mathematically correct. The point to make here is that we must continue to factor out a perfect square whenever possible. Our answer is not in simple radical form until we can no longer factor out a perfect square.

Exercise $\PageIndex{3}$

Place $\sqrt{200}$ in simple radical form.

Answer: $10\sqrt{2}$

The Pythagorean Theorem

An angle that measures $90$ degrees is called a right angle. If one of the angles of a triangle is a right angle, then the triangle is called a right triangle. It is traditional to mark the right angle with a little square (see Figure $\PageIndex{2}$).

fig 8.2.2.png — Figure $\PageIndex{2}$: Right triangle $\triangle A B C$ has a right angle at vertex $C$.

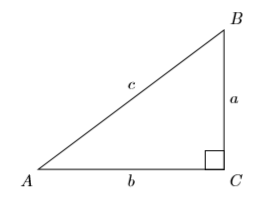
Right Triangle Terminology

The longest side of the right triangle, the side directly opposite the right angle, is called the hypotenuse of the right triangle.
The remaining two sides of the right triangle are called the legs of the right triangle.

Proof of the Pythagorean Theorem

Each side of the square in Figure $\PageIndex{3}$ has been divided into two segments, one of length $a$, the other of length $b$.

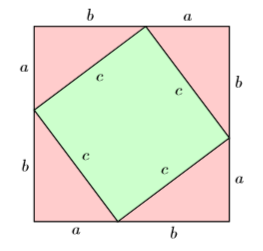
fig 8.2.3.png — Figure $\PageIndex{3}$: Proving the Pythagorean Theorem.

We can ﬁnd the total area of the square by squaring any one of the sides of the square.

\[\begin{array}{ll}{A=(a+b)^{2}} & \color {Red} {\text { Square a side to find area. }} \\ {A=a^{2}+2 a b+b^{2}} & \color {Red} {\text { Squaring a binomial pattern. }}\end{array} \nonumber\]

Thus, the total area of the square is $A = a^2 +2ab + b^2$.

A second approach to ﬁnding the area of the square is to sum the areas of the geometric parts that make up the square. We have four congruent right triangles, shaded in light red, with base $a$ and height $b$. The area of each of these triangles is found by taking one-half times the base times the height; i.e., the area of each triangles is $(1 / 2) a b$. In the interior, we have a smaller square with side $c$. Its area is found by squaring its side; i.e., the area of the smaller square is $c^2$.

The total area of the square is the sum of its parts, one smaller square and four congruent triangles. That is:

\[\begin{array}{ll}{A=c^{2}+4\left(\frac{1}{2} a b\right)} & \color {Red} {\text { Adding the area of the interior square and the area of four right triangles. }} \\ {A=c^{2}+2 a b} & \color {Red} {\text { Simplify: } 4((1 / 2) a b)=2 a b}\end{array} \nonumber \]

The two expressions, $a^2 +2ab+ b^2$ and $c^2 +2ab$, both represent the total area of the large square. Hence, they must be equal to one another.

\[\begin{aligned} a^{2}+2 a b+b^{2}=c^{2}+2 a b & \quad \color {Red} \text { Each side of this equation represents the area of the large square. } \\ a^{2}+b^{2}=c^{2} & \quad \color {Red} \text { Subtract } 2 a b \text { from both sides. } \end{aligned} \nonumber \]

The last equation, $a^2 + b^2 = c^2$, is called the Pythagorean Theorem.

The Pythagorean Theorem

If $a$ and $b$ are the legs of a right triangle and $c$ is its hypotenuse, then:

\[a^2 + b^2 = c^2 \nonumber \]

We say “The sum of the squares of the legs of a right triangle equals the square of its hypotenuse.”

Good hint: Note that the hypotenuse sits by itself on one side of the equation $a^2 + b^2 = c^2$. The legs of the hypotenuse are on the other side.

Let’s put the Pythagorean Theorem to work.

Example $\PageIndex{4}$

Find the length of the missing side of the right triangle shown below.

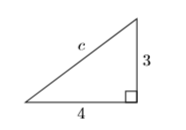
$fig 8.2.4.png$

Solution

First, write out the Pythagorean Theorem, then substitute the given values in the appropriate places.

\[\begin{aligned} a^{2}+b^{2}=c^{2} & \color {Red} \text { Pythagorean Theorem. } \\(4)^{2}+(3)^{2}=c^{2} & \color {Red} \text { Substitute: } 4 \text { for } a, 3 \text { for } b \\ 16+9=c^{2} & \color {Red} \text { Square: }(4)^{2}=16,(3)^{2}=9 \\ 25=c^{2} & \color {Red} \text { Add: } 16+9=25 \end{aligned} \nonumber \]

The equation $c^2 = 25$ has two real solutions, $c = −5$ and $c = 5$. However, in this situation, $c$ represents the length of the hypotenuse and must be a positive number. Hence:

\[c=5 \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Thus, the length of the hypotenuse is $5$.

Exercise $\PageIndex{4}$

Find the missing side of the right triangle shown below.

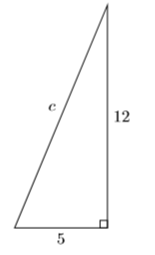
$Ex 8.2.4.png$

Answer: $13$

Example $\PageIndex{5}$

An isosceles right triangle has a hypotenuse of length $8$. Find the lengths of the legs.

Solution

In general, an isosceles triangle is a triangle with two equal sides. In this case, an isosceles right triangle has two equal legs. We’ll let $x$ represent the length of each leg.

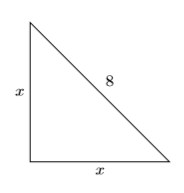
$fig 8.2.5.png$

Use the Pythagorean Theorem, substituting $x$ for each leg and $8$ for the hypotenuse.

\[\begin{array}{rlrl}{a^{2}+b^{2}} & {=c^{2}} & {} & \color {Red} {\text { Pythagorean Theorem. }} \\ {x^{2}+x^{2}} & {=8^{2}} & {} & \color {Red} {\text { Substitute: } x \text { for } a, x \text { for } b, 8 \text { for } c .} \\ {2 x^{2}} & {=64} & {} & \color {Red} {\text { Combine like terms: } x+x=2 x} \\ {x^{2}} & {=32} & {} & \color {Red} {\text { Divide both sides by } 2}\end{array} \nonumber \]

The equation $x^2 = 32$ has two real solutions, $x=-\sqrt{32}$ and $x=\sqrt{32}$. However, in this situation, $x$ represents the length of each leg and must be a positive number. Hence:

\[x=\sqrt{32} \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Remember, your ﬁnal answer must be in simple radical form. We must factor out a perfect square when possible.

\[\begin{array}{ll}{x=\sqrt{16} \sqrt{2}} & \color {Red} {\text { Factor out a perfect square. }} \\ {x=4 \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]

Thus, the length of each leg is $4\sqrt{2}$.

Exercise $\PageIndex{5}$

An isosceles right triangle has a hypotenuse of length $10$. Find the lengths of the legs.

Answer: Each leg has length $5\sqrt{2}$

Applications

Let’s try a word problem.

Example $\PageIndex{6}$

A ladder $20$ feet long leans against the garage wall. If the base of the ladder is $8$ feet from the garage wall, how high up the garage wall does the ladder reach? Find an exact answer, then use your calculator to round your answer to the nearest tenth of a foot.

Solution

As always, we obey the Requirements for Word Problem Solutions.

Set up a variable dictionary. We’ll create a well-marked diagram for this purpose, letting $h$ represent the distance between the base of the garage wall and the upper tip of the ladder.

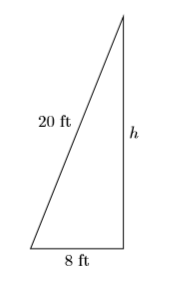
$fig 8.2.6.png$

Set up an equation. Using the Pythagorean Theorem, we can write:\[\begin{array}{ll}{8^{2}+h^{2}=20^{2}} & \color {Red} {\text { Pythagorean Theorem. }} \\ {64+h^{2}=400} & \color {Red} {\text { Square: } 8^{2}=64 \text { and } 20^{2}=400}\end{array} \nonumber \]
Solve the equation.\[\begin{array}{ll}{h^{2}=336} & \color {Red} {\text { Subtract } 64 \text { from both sides. }} \\ {h=\sqrt{336}} & \color {Red} {h \text { will be the nonnegative square root. }} \\ {h=\sqrt{16} \sqrt{21}} & \color {Red} {\text { Factor out a perfect square. }} \\ {h=4 \sqrt{21}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]
Answer the question. The ladder reaches $4 \sqrt{21}$ feet up the wall. Using a calculator, this is about $18.3$ feet, rounded to the nearest tenth of a foot.
Look back. Understand that when we use $18.3$ ft, an approximation, our solution will only check approximately.

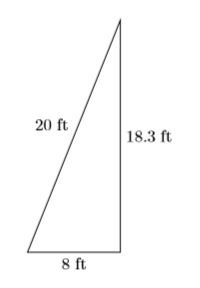
$fig 8.2.7.png$

Using the Pythagorean Theorem: \[\begin{array}{r}{8^{2}+18.3^{2} \stackrel{?}{=} 20^{2}} \\ {64+334.89 \stackrel{?}{=} 400} \\ {398.89 \stackrel{?}{=} 400}\end{array} \nonumber \]The approximation is not perfect, but it seems close enough to accept this solution.

Exercise $\PageIndex{6}$

A ladder $15$ feet long leans against a wall. If the base of the ladder is $6$ feet from the wall, how high up the wall does the ladder reach? Use your calculator to round your answer to the nearest tenth of a foot.

Answer: $13.7$ feet.

Search

Text Color

Text Size

Margin Size

Font Type