8.3: Completing the Square

In Introduction to Radical Notation, we showed how to solve equations such as $x^2 = 9$ both algebraically and graphically.

$$\begin{aligned} x^{2} &=9 \\ x &=\pm 3 \end{aligned} \nonumber$$

Figure $\PageIndex{1}$

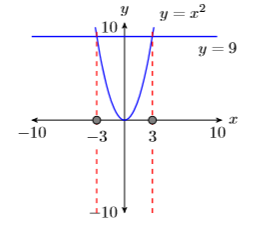
Note that when we take the square root of both sides of this equation, there are two answers, one negative and one positive.

A perfect square is nice, but not required. Indeed, we may even have to factor out a perfect square to put our final answer in simple form.

$$\begin{aligned} x^{2} &=8 \\ x &=\pm \sqrt{8} \\ x &=\pm \sqrt{4} \sqrt{2} \\ x &=\pm 2 \sqrt{2} \end{aligned} \nonumber$$

Figure $\PageIndex{2}$

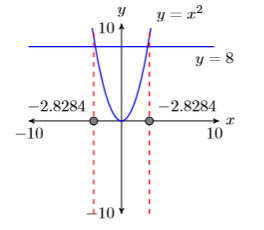
Readers should use their calculators to check that $-2 \sqrt{2} \approx -2.8284$ and $2 \sqrt{2} \approx 2.8284$.

Now, let’s extend this solution technique to a broader class of equations.

Example $\PageIndex{1}$

Solve for $x : (x-4)^{2}=9$

Solution

Much like the solutions of $x^2 = 9$ are $x = ±3$, we use a similar approach on $(x−4)^2 = 9$ to obtain:

$$\begin{array}{rlrl}{(x-4)^{2}} & {=9} & {} & \color {Red} {\text { Original equation. }} \\ {x-4} & {=\pm 3} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber$$

To complete the solution, add $4$ to both sides of the equation.

$$x=4 \pm 3 \quad \color {Red} \text { Add } 3 \text { to both sides. } \nonumber$$

Note that this means that there are two answers, namely:

$$\begin{array}{l}{x=4-3} \\ {x=1}\end{array} \nonumber$$

or

$$\begin{array}{l}{x=4+3} \\ {x=7}\end{array} \nonumber$$

Check: Check each solution by substituting it into the original equation.

Substitute $1$ for $x$:

$$\begin{aligned}(x-4)^{2} &=9 \\(1-4)^{2} &=9 \\(-3)^{2} &=9 \end{aligned} \nonumber$$

Substitute $7$ for $x$:

$$\begin{aligned}(x-4)^{2} &=9 \\(7-4)^{2} &=9 \\(3)^{2} &=9 \end{aligned} \nonumber$$

Because the last statement in each check is a true statement, both $x = 1$ and $x = 7$ are valid solutions of $(x−4)^2 = 9$.

Exercise $\PageIndex{1}$

Solve for $x :(x+6)^{2}=10$

Answer

$-2$, $-10$

In Example $\PageIndex{1}$, the right-hand side of the equation $(x−4)^2 = 9$ was a perfect square. However, this is not required, as the next example will show.

Example $\PageIndex{2}$

Solve for $x :(x+5)^{2}=7$

Solution

Using the same technique as in Example $\PageIndex{1}$, we obtain:

$$\begin{array}{rlrl}{(x+5)^{2}} & {=7} & {} & \color {Red} {\text { Original equation. }} \\ {x+5} & {=\pm \sqrt{7}} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber$$

To complete the solution, subtract 5 from both sides of the equation.

$$x=-5 \pm \sqrt{7} \quad \color {Red} \text { Subtract } 5 \text { from both sides.} \nonumber$$

Note that this means that there are two answers, namely:

$$x=-5-\sqrt{7} \quad \text { or } \quad x=-5+\sqrt{7} \nonumber$$

Check: Check each solution by substituting it into the original equation.

Substitute $-5-\sqrt{7}$ for $x$:

$$\begin{aligned}(x+5)^{2} &=7 \\((-5-\sqrt{7})+5)^{2} &=7 \\(-\sqrt{7})^{2} &=7 \end{aligned} \nonumber$$

Substitute $-5+\sqrt{7}$ for $x$:

$$\begin{aligned}(x+5)^{2} &=7 \\((-5+\sqrt{7})+5)^{2} &=7 \\(\sqrt{7})^{2} &=7 \end{aligned} \nonumber$$

Because the last statement in each check is a true statement, both $x=-5-\sqrt{7}$ and $x=-5+\sqrt{7}$ are valid solutions of $(x+5)^{2}=7$.

Exercise $\PageIndex{2}$

Solve for $x :(x-4)^{2}=5$

Answer

$4+\sqrt{5}, 4-\sqrt{5}$

Sometimes you will have to factor out a perfect square to put your answer in simple form.

Example $\PageIndex{3}$

Solve for $x :(x+4)^{2}=20$

Solution

Using the same technique as in Example $\PageIndex{1}$, we obtain:

$$\begin{array}{rlrl}{(x+4)^{2}} & {=20} & {} & \color {Red} {\text { Original equation. }} \\ {x+4} & {=\pm \sqrt{20}} & {} & \color {Red} {\text { There are two square roots. }} \\ {x+4} & {=\pm \sqrt{4} \sqrt{5}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x+4} & {=\pm 2 \sqrt{5}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber$$

To complete the solution, subtract $4$ from both sides of the equation.

$$x=-4 \pm 2 \sqrt{5} \quad \color {Red} \text { Subtract } 4 \text { from both sides. } \nonumber$$

Note that this means that there are two answers, namely:

$$x=-4-2 \sqrt{5} \quad \text { or } \quad x=-4+2 \sqrt{5} \nonumber$$

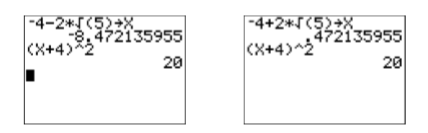
Check: Although it is possible to check the exact answers, let’s use our calculator instead. First, store $-4-2 \sqrt{5}$ in $\mathbf{X}$. Next, enter the left-hand side of the equation $(x + 4)^2 = 20$ (see image on the left in Figure $\PageIndex{3}$). Note that (x+4)2 simplifies to 20, showing that $-4-2 \sqrt{5}$ is a solution of $(x+4)^2 = 20$.

In similar fashion, the solution $-4+2 \sqrt{5}$ also checks in $(x + 4)^2 = 20$ (see image on the right in Figure $\PageIndex{3}$).

Figure $\PageIndex{3}$: Checking $-4-2 \sqrt{5}$ and $-4+2 \sqrt{5}$ in the equation $(x+4)^2 = 20$.

Exercise $\PageIndex{3}$

Solve for $x :(x+7)^{2}=18$

Answer

$-7+3 \sqrt{2},-7-3 \sqrt{2}$

Perfect Square Trinomials Revisited

Recall the squaring a binomial shortcut.

Squaring a Binomial

If $a$ and $b$ are any real numbers, then: $$(a±b)^2 = a^2 ±2ab + b^2 \nonumber$$ That is, you square the first term, take the product of the first and second terms and double the result, then square the third term.

Reminder examples:

$$\begin{aligned}(x+3)^{2} &=x^{2}+2(x)(3)+3^{2} \\ &=x^{2}+6 x+9 \end{aligned} \nonumber$$

$$\begin{aligned}(x-8)^{2} &=x^{2}-2(x)(8)+8^{2} \\ &=x^{2}-16 x+64 \end{aligned} \nonumber$$

Because factoring is “unmultiplying,” it is a simple matter to reverse the multiplication process and factor these perfect square trinomials.

$$x^{2}+6 x+9=(x+3)^{2} \nonumber$$

$$x^{2}-16 x+64=(x-8)^{2} \nonumber$$

Note how in each case we simply take the square root of the first and last terms.

Example $\PageIndex{4}$

Factor each of the following trinomials:

1. $x^{2}-12 x+36$
2. $x^{2}+10 x+25$
3. $x^{2}-34 x+289$

Solution

Whenever the first and last terms of a trinomial are perfect squares, we should suspect that we have a perfect square trinomial.

1. The first and third terms of $x^{2}-12 x+36$ are perfect squares. Hence, we take their square roots and try: $$x^{2}-12 x+36=(x-6)^{2} \nonumber$$ Note that $2(x)(6)=12 x$, which is the middle term on the left. The solution checks.
2. The first and third terms of $x^{2}+10 x+25$ are perfect squares. Hence, we take their square roots and try: $$x^{2}+10 x+25=(x+5)^{2} \nonumber$$ Note that $2(x)(5)=10 x$, which is the middle term on the left. The solution checks.
3. The first and third terms of $x^{2}-34 x+289$ are perfect squares. Hence, we take their square roots and try: $$x^{2}-34 x+289=(x-17)^{2} \nonumber$$ Note that $2(x)(17)=34 x$, which is the middle term on the left. The solution checks.

Exercise $\PageIndex{4}$

Factor: $x^2 + 30x + 225$

Answer

$(x+15)^{2}$

Completing the Square

In this section we start with the binomial $x^2 +bx$ and ask the question “What constant value should we add to $x^2 + bx$ so that the resulting trinomial is a perfect square trinomial?” The answer lies in this procedure.

Completing the square

To calculate the constant required to make $x^2 +bx$ a perfect square trinomial:

1. Take one-half of the coefficient of $x : \dfrac{b}{2}$
2. Square the result of step one: $\left(\dfrac{b}{2}\right)^{2}=\dfrac{b^{2}}{4}$
3. Add the result of step two to $x^{2}+b x : x^{2}+b x+\dfrac{b^{2}}{4}$

If you follow this process, the result will be a perfect square trinomial which will factor as follows:

$$x^{2}+b x+\dfrac{b^{2}}{4}=\left(x+\dfrac{b}{2}\right)^{2} \nonumber$$

Example $\PageIndex{5}$

Given $x^2 + 12 x$, complete the square to create a perfect square trinomial.

Solution

Compare $x^2 + 12x$ with $x^2 + bx$ and note that $b = 12$.

1. Take one-half of $12: 6$
2. Square the result of step one: $6^2 = 36$
3. Add the result of step two to $x^2 + 12x: x^2 + 12x + 36$

Check: Note that the first and last terms of $x^2 +12x+36$ are perfect squares. Take the square roots of the first and last terms and factor as follows:

$$x^{2}+12 x+36=(x+6)^{2} \nonumber$$

Note that $2(x)(6) = 12x$, so the middle term checks.

Exercise $\PageIndex{5}$

Given $x^2 + 16x$, complete the square to create a perfect square trinomial.

Answer

$x^{2}+16 x+64=(x+8)^{2}$

Example $\PageIndex{6}$

Given $x^2−3x$, complete the square to create a perfect square trinomial.

Solution

Compare $x^2 −3x$ with $x^2 + bx$ and note that $b =−3$.

1. Take one-half of $-3 : -\dfrac{3}{2}$
2. Square the result of step one: $\left(-\dfrac{3}{2}\right)^{2}=\dfrac{9}{4}$
3. Add the result of step two to $x^{2}-3 x : x^{2}-3 x+\dfrac{9}{4}$

Check: Note that the first and last terms of $x^{2}-3 x+\dfrac {9}{4}$ are perfect squares. Take the square roots of the first and last terms and factor as follows:

$$x^{2}-3 x+\dfrac{9}{4}=\left(x-\dfrac{3}{2}\right)^{2} \nonumber$$

Note that $2(x)\left (\dfrac {3}{2} \right)=3 x$, so the middle term checks.

Exercise $\PageIndex{6}$

Given $x^2 −5x$, complete the square to create a perfect square trinomial.

Answer

$x^{2}-5 x+\dfrac {10}{4}=\left(x-\dfrac {5}{2} \right)^{2}$

Solving Equations by Completing the Square

Consider the following nonlinear equation.

$$x^2 =2x +2 \nonumber$$

The standard approach is to make one side zero and factor. $$x^2 −2x−2=0 \nonumber$$ However, one quickly realizes that there is no integer pair whose product is $ac = −2$ and whose sum is $b = −2$. So, what does one do in this situation? The answer is “Complete the square.”

Example $\PageIndex{7}$

Use completing the square to help solve $x^2 =2x + 2$.

Solution

First, move $2x$ to the left-hand side of the equation, keeping the constant $2$ on the right-hand side of the equation. $$x^2 −2x =2 \nonumber$$ On the left, take one-half of the coefficient of $x: \left (\dfrac{1}{2} \right)(-2)=-1$. Square the result: $(-1)^{2}=1$. Add this result to both sides of the equation.

$$\begin{array}{l}{x^{2}-2 x+1=2+1} \\ {x^{2}-2 x+1=3}\end{array} \nonumber$$

We can now factor the left-hand side as a perfect square trinomial.

$$(x-1)^{2}=3 \nonumber$$

Now, as in Examples $\PageIndex{1}$, $\PageIndex{2}$, and $\PageIndex{3}$, we can take the square root of both sides of the equation. Remember, there are two square roots.

$$x-1=\pm \sqrt{3} \nonumber$$

Finally, add $1$ to both sides of the equation.

$$x=1 \pm \sqrt{3} \nonumber$$

Thus, the equation $x^2 =2x+ 2$ has two answers, $x=1-\sqrt{3}$ and $x=1+\sqrt{3}$.

Check: Let’s use the calculator to check the solutions. First, store $1-\sqrt{3}$ in $\mathbf{X}$ (see the image on the left in Figure $\PageIndex{4}$). Then enter the left- and right-hand sides of the equation $x^2 =2 x + 2$ and compare the results (see the image on the left in Figure $\PageIndex{4}$). In similar fashion, check the second answer $1+\sqrt{3}$ (see the image on the right in Figure $\PageIndex{4}$).

Figure $\PageIndex{4}$: Checking $1-\sqrt{3}$ and $1+\sqrt{3}$ in the equation $x^2 =2x + 2$.

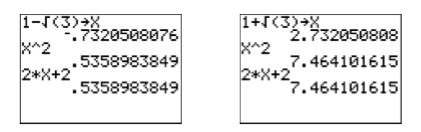
In both cases, note that the left- and right-hand sides of $x^2 =2x+2$ produce the same result. Hence, both $1-\sqrt{3}$ and $1+\sqrt{3}$ are valid solutions of $x^2 =2x+2$.

Exercise $\PageIndex{7}$

Use completing the square to help solve $x^2 =3−6x$.

Answer

$-3+2 \sqrt{3},-3-2 \sqrt{3}$

Example $\PageIndex{8}$

Solve the equation $x^2 −8x−12 = 0$, both algebraically and graphically. Compare your answer from each method.

Solution

First, move the constant $12$ to the right-hand side of the equation.

$$\begin{aligned} x^{2}-8 x-12=0 & \quad \color {Red} \text { Original equation. } \\ x^{2}-8 x=12 & \quad \color {Red} \text { Add } 12 \text { to both sides. } \end{aligned} \nonumber$$

Take half of the coefficient of $x :(1 / 2)(-8)=-4$. Square: $(-4)^{2}=16$. Now add $16$ to both sides of the equation.

$$\begin{aligned} x^{2}-8 x+16 & =12+16 \quad \color {Red} \text { Add } 16 \text { to both sides. } \\ (x-4)^{2} & =28 \quad \color {Red} \text { Factor left-hand side. } \\ x-4 &=\pm \sqrt{28} \quad \color {Red} \text { There are two square roots. }\end{aligned} \nonumber$$
Note that the answer is not in simple radical form.

$$\begin{array}{rlrl}{x-4} & {=\pm \sqrt{4} \sqrt{7}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x-4} & {=\pm 2 \sqrt{7}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {x} & {=4 \pm 2 \sqrt{7}} & {} & \color {Red} {\text { Add } 4 \text { to both sides. }}\end{array} \nonumber$$

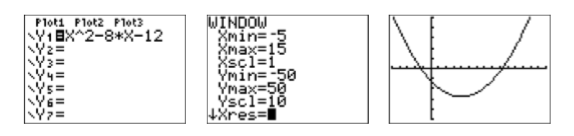
Graphical solution: Enter the equation $y = x^2 − 8x − 12$ in $\mathbf{Y1}$ of the Y= menu (see the first image in Figure $\PageIndex{5}$). After some experimentation, we settled on the WINDOW parameters shown in the middle image of Figure $\PageIndex{5}$. Once you’ve entered these WINDOW parameters, push the GRAPH button to produce the rightmost image in Figure $\PageIndex{5}$.

Figure $\PageIndex{5}$: Drawing the graph of $y = x^2 −8x−12$.

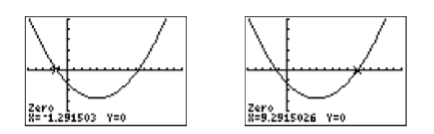
We’re looking for solutions of $x^2 −8x−12 = 0$, so we need to locate where the graph of $y = x^2 −8x−12$ intercepts the $x$-axis. That is, we need to find the zeros of $y = x^2 −8x−12$. Select 2:zero from the CALC menu, move the cursor slightly to the left of the first $x$-intercept and press ENTER in response to “Left bound.” Move the cursor slightly to the right of the first $x$-intercept and press ENTER in response to “Right bound.” Leave the cursor where it sits and press ENTER in response to “Guess.” The calculator responds by finding the $x$-coordinate of the $x$-intercept, as shown in the first image in Figure $\PageIndex{6}$.

Repeat the process to find the second $x$-intercept of $y = x^2−8x−12$ shown in the second image in Figure $\PageIndex{6}$.

Figure $\PageIndex{6}$: Calculating the zeros of $y = x^2 −8x−12$.

Reporting the solution on your homework: Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.

• Label the horizontal and vertical axes with $x$ and $y$, respectively (see Figure $\PageIndex{7}$).
• Place your WINDOW parameters at the end of each axis (see Figure $\PageIndex{7}$).
• Label the graph with its equation (see Figure $\PageIndex{7}$).
• Drop dashed vertical lines through each $x$-intercept. Shade and label the $x$-values of the points where the dashed vertical line crosses the $x$-axis. These are the solutions of the equation $x^2−8x−12 = 0$ (see Figure $\PageIndex{7}$).

Figure $\PageIndex{7}$: Reporting your graphical solution on your homework.

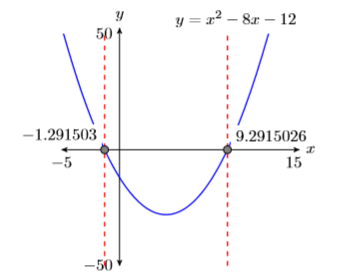
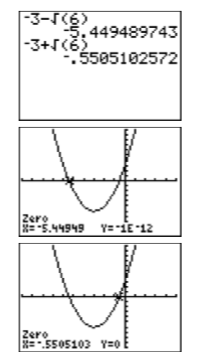
Thus, the graphing calculator reports that the solutions of $x^2 −8x−12 = 0$ are $x \approx-1.291503$ and $x \approx 9.2915026$.

Comparing exact and calculator approximations: How well do the graphing calculator solutions compare with the exact solutions, $x=4-2 \sqrt{7}$ and $x=4+2 \sqrt{7}$? After entering each in the calculator (see Figure $\PageIndex{8}$), the comparison is excellent!

Figure $\PageIndex{8}$: Approximating exact solutions $x=4-2 \sqrt{7}$ and $x=4+2 \sqrt{7}$.

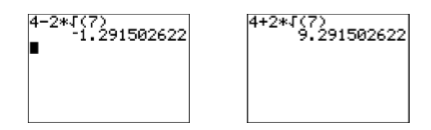
Exercise $\PageIndex{8}$

Solve the equation $x^2 +6x + 3 = 0$ both algebraically and graphically, then compare your answers.

Answer

$-3-\sqrt{6},-3+\sqrt{6}$