10.5: Solving Quadratic Equations Using the Method of Completing the Square
- Page ID
- 49405
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Logic Behind The Method
Suppose we wish to solve the quadratic equation \(x^2 - 3x - 1 = 0\). Since the equation is not of the form \(x^2 = K\), we cannot use extraction of roots. Next, we try factoring, but after a few trials we see that \(x^2 - 3x - 1\) is not factorable. We need another method for solving quadratic equations.
The method we shall study is based on perfect square trinomials and extraction of roots. The method is called solving quadratic equations by completing the square. Consider the equation
\[x^2 + 6x + 5 = 0.\]
This quadratic equation could be solved by factoring, but we'll use the method of completing the square. We will explain the method in detail after we look at this example. First we'll rewrite the equation as
\[x^2 + 6x = -5\]
Then, we'll add \(9\) to each side. We get
\[x^2 + 6x + 9 = -5 + 9\]
The left side factors as a perfect square trinomial.
\[(x + 3)^2 = 4\]
We can solve this by the extraction of roots.
\[\begin{array}{flushleft}
x + 3 &= \pm \sqrt{4}\\
x + 3 &= \pm 2\\
x &= \pm 2 - 3\\
x &= + 2 - 3 & \text{ and } & x = -2 - 3\\
x &= -1 & \text{ and } -5
\end{array}\]
Notice that when the roots are rational numbers, the equation is factorable.
The big question is, "How did we know to add 9 to each side of the equation?" We can convert any quadratic trinomial appearing in an equation into a perfect square trinomial if we know what number to add to both sides. We can determine that particular number by observing the following situation:
Consider the square of the binomial and the resulting perfect square trinomial
\[(x + p)^2 = x^2 + 2px + p^2\]
Notice that the constant term (the number we are looking for) can be obtained from the linear term \(2px\). If we take one half the coefficient of \(x\), \(\dfrac{20}{2} = p\), and square it, we get the constant term \(p^2\). This is true for every perfect square trinomial with a leading coefficient \(1\).
In a perfect square trinomial with leading coefficient \(1\), the constant term is the square of one-half the coefficient of the linear term.
Study these examples to see what constant term will make the given binomial into a perfect square trinomial.
\(x^2 + 6x\). The constant must be the square of one half the coefficient of \(x\). Since the coefficient of \(x\) is \(6\), we have
\(\dfrac{6}{2} = 3\) and \(3^2 = 9\)
The constant is \(9\).
\[x^2 + 6x + 9 = (x + 3)^2\]
This is a perfect square trinomial.
\(a^2 + 10a\). The constant must be the square of one half the coefficient of \(a\). Since the coefficient of \(a\) is \(10\), we have
\(\dfrac{10}{2} = 5\) and \(5^2 = 25\).
The constant is \(25\)
\[a^2 + 10a + 25 = (a + 5)^2\]
\(y^2 + 3y\). The constant must be the square of one-half the coefficient of \(y\). Since the coefficient of \(y\) is \(3\), we have
\(\dfrac{3}{2}\) and \((\dfrac{3}{2})^2 = \dfrac{9}{4}\)
The constant is \(\dfrac{9}{4}\).
\[y^2 + 3y + \dfrac{9}{4} = (y + \dfrac{3}{2})^2\]
The Method Of Completing The Square
Now, with these observations, we can describe the method of completing the square.
- Write the equation so that the constant term appears on the right side of the equation.
- If the leading coefficient is different from 1, divide each term of the equation by that coefficient.
- Take one half of the coefficient of the linear term, square it, then add it to both sides of the equation.
- The trinomial on the left is now a perfect square trinomial and can be factored as \(()^2\). The first term in the parentheses is the square root of the quadratic term. The last term in the parentheses is one-half the coefficient of the linear term.
- Solve this equation by extraction of roots.
Sample Set A
Solve the following equations.
\(\begin{array}{flushleft}
x^2 + 8x - 9 &= 0 & \text{ Add } 9 \text{ to both sides.}\\
x^2 + 8x &= 9 & \text{ One half the coefficient of } x \text{ is } 4, \text{ and } 4^2 \text{ is } 16. \text{ Add } 16 \text{ to both sides. }\\
x^2 + 8x + 16 &= 9 + 16\\
x^2 + 8x + 16 &= 25 & \text{ Factor. }\\
(x+4)^2 &= 25 & \text{ Take square roots. }\\
x + 4 &= \pm 5\\
x &= \pm 5 - 4 & +5 - 4 = 1, -5 - 4 = -9\\
x &= 1, -9
\end{array}\)
\(\begin{array}{flushleft}
x^2 - 3x - 1 &= 0 & \text{ Add } 1 \text{ to both sides.}\\
&& \text{ One half the coefficient of } x \text{ is } \dfrac{-3}{2}.\\
x^2 - 3x &= 1 & \text{ Square it: } (\dfrac{-3}{2})^2 = \dfrac{9}{4}. \text{ Add } \dfrac{9}{4} \text{to each side.}\\
x^2 - 3x + \dfrac{9}{4} &= 1 + \dfrac{9}{4}\\
x^2 - 3x + \dfrac{9}{4} &= \dfrac{13}{4} & \text{Factor. Notice that since the sign of the middle term of the trinomial is "-", its factored form has a "-" sign.}\\
(x - \dfrac{3}{2})^2 &= \dfrac{13}{4} & \text{ Now take square roots }\\
x - \dfrac{3}{2} &= \pm \sqrt{\dfrac{13}{4}}\\
x - \dfrac{3}{2} &= \pm \sqrt{\dfrac{13}{2}}\\
x &= \pm \dfrac{\sqrt{13}}{2} + \dfrac{3}{2}\\
x &= \dfrac{\pm \sqrt{13} + 3}{2}\\
x &= \dfrac{3 \pm \sqrt{13}}{2}
\end{array}\)
\(\begin{array}{flushleft}
3a^2 - 36a - 39 &= 0 & \text{ Add } 39 \text{ to both sides.}\\
3a^2 - 36a &= 39 & \text{ The leading coefficient is } 3 \text{ and we need it to be } 1. \text{ Divide each term by } 3 \text{. One half of the coefficient of } a \text{ is } -6\\
a^2 - 12a &= 13 & \text{ Square it: } (-6)^2 = 36 \text{ Add } 36 \text{ to each side. }\\
a^2 - 12a + 36 &= 13 + 36\\
a^2 - 12a + 36 &= 49\\
(a-6)^2 &= 49 & \text{ Factor. }\\
a - 6 &= \pm 7\\
a &= \pm 7 + 6 & +7 + 6 = 13, -7 + 6 = -1
\end{array}\)
\(a = 13, -1\).
\(\begin{array}{flushleft}
2x^2 + x + 4 &= 0\\
2x^2 + x &= -4\\
x^2 + \dfrac{1}{2}x &= -2\\
x^2 + \dfrac{1}{2}x + (\dfrac{1}{4})^2 &= -2 + (\dfrac{1}{4})^2
\end{array}\)
\((x + \dfrac{1}{4})^2 = -2 + \dfrac{1}{16} = \dfrac{-32}{16} + \dfrac{1}{16} = \dfrac{-31}{16}\)
Since we know that the square of any number is positive, this equation has no real number solution.
Calculator Problem:
Solve \(7a^2 - 5a - 1 = 0\). Round each solution to the nearest tenth.
\(\begin{array}{flushleft}
7a^2 - 5a - 1 &= 0\\
7a^2 - 5a &= 1\\
a^2 - \dfrac{5}{7}a &= \dfrac{1}{7}\\
a^2 - \dfrac{5}{7}a + (\dfrac{5}{14})^2 &= \dfrac{1}{7} + (\dfrac{5}{14})^2\\
(a - \dfrac{5}{14})^2 &= \dfrac{1}{7} + \dfrac{25}{196} &= \dfrac{28}{196} + \dfrac{25}{196} = \dfrac{53}{196}\\
a - \dfrac{5}{14} &= \pm \sqrt{\dfrac{53}{196}} &= \pm \dfrac{\sqrt{53}}{14}
\end{array}\)
\(a = \dfrac{5}{14} \pm \dfrac{\sqrt{53}}{14} = \dfrac{5 \pm \sqrt{53}}{14}\)
Rounding to tenths, we get \(a \approx -0.2\). Thus, \(a \approx 0.9\) and \(-0.2\) to the nearest tenth.
Practice Set A
Solve each of the following quadratic equations using the method of completing the square.
\(x^2 - 2x - 48 = 0\)
- Answer
-
\(x=−6, 8\)
\(x^2 + 3x - 5 = 0\)
- Answer
-
\(x = \dfrac{-3 \pm \sqrt{29}}{2}\)
\(4m^2 + 5m = -1\)
- Answer
-
\(m = \dfrac{-1}{4}, -1\)
\(5y^2 - 2y - 4 = 0\)
- Answer
-
\(y = \dfrac{1 \pm \sqrt{21}}{5}\)
Calculator problem:
Solve \(3x^2 - x - 1= 0\). Round each solution to the nearest tenth.
- Answer
-
\(x = 0.8, -0.4\)
Exercises
For the following problems, solve the equations by completing the square.
\(x^2 +2x - 8 = 0\)
- Answer
-
\(x=−4, 2\)
\(y^2 - 5y - 6 = 0\)
\(a^2 + 7a + 12 = 0\)
- Answer
-
\(a=−3, −4\)
\(x^2 - 10x + 16 = 0\)
\(y^2 - 2y - 24 = 0\)
- Answer
-
\(y = -4, 6\)
\(a^2 + 2a - 35 = 0\)
\(x^2 + 2x + 5 = 0\)
- Answer
-
No real number solution.
\(x^2 - 6x + 1 = 0\)
\(x^2 + 4x + 4 = 0\)
- Answer
-
\(x=−2\)
\(a^2 + 4a + 7 = 0\)
\(b^2 + 5b - 3 = 0\)
- Answer
-
\(b = \dfrac{-5 \pm \sqrt{37}}{2}\)
\(b^2 - 6b = 72\)
\(a^2 + 10a - 9 = 0\)
- Answer
-
\(a = -5 \pm \sqrt{34}\)
\(a^2 - 2a - 3 = 0\)
\(x^2 - 10x = 0\)
- Answer
-
\(x=10, 0\)
\(y^2 - 8y = 0\)
\(a^2 - 6a = 0\)
- Answer
-
\(a = 6, 0\)
\(b^2 + 6b = 0\)
\(-x^2 - 14x = 13\)
- Answer
-
\(x=−13, −1\)
\(-x^2 +8x = -84\)
\(2a^2 + 2a - 1 = 0\)
- Answer
-
\(a = \dfrac{-1 \pm \sqrt{3}}{2}\)
\(4b^2 - 8b = 16\)
\(9x^2 + 12x - 5 = 0\)
- Answer
-
\(x = \dfrac{1}{3}, -\dfrac{5}{3}\)
\(16y^2 - 8y - 3 = 0\)
\(2x^2 + 5x - 4 = 0\)
- Answer
-
\(x = \dfrac{-5 \pm \sqrt{57}}{4}\)
\(3a^2 + 2a - 24 = 0\)
\(x^2 + 2x + 8 = 0\)
- Answer
-
No real number solution.
\(y^2 - 3y + 10 = 0\)
\(7a^2 + 3a - 1 = 0\)
- Answer
-
\(a = \dfrac{-3 \pm \sqrt{37}}{14}\)
Calculator Problems
For the following problems, round each solution to the nearest hundredth.
\(5m^2 - 2m - 6 = 0\)
\(3y^2 + 5y = 7\)
- Answer
-
\(y=0.91, −2.57\)
\(1.8x^2 + 2.3x - 4.1 = 0\)
\(0.04a^2 - 0.03a + 0.02 = 0\)
- Answer
-
No real number solution.
Exercises For Review
Factor \(12ax - 6bx + 20ay - 10by\) by grouping.
Graph the compound inequality \(-6 \le -2x + 2 < -4\)
- Answer
-
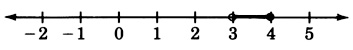
Find the equation of the line that passes through the points \((1, -2)\) and \((0, 4)\)
Find the product: \(\dfrac{x^2 - 4x - 12}{x^2 - 2x - 8} \cdot \dfrac{x^2 - 3x - 4}{x^2 - 3x - 18}\)
- Answer
-
\(\dfrac{x+1}{x+3}\)
Use the method of extraction of roots to solve \((x-2)^2 = 25\)