8.4: The Quadratic Formula

Last updated
Save as PDF

Page ID: 19901

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We ﬁrst start with the deﬁnition of a quadratic equation.

Quadratic equation

A second degree polynomial equation of the form \[ax^2 + bx + c =0 \nonumber \]where $a$, $b$, and $c$ are any real numbers, is called a quadratic equation in $x$.

The goal of this section is to develop a formulaic shortcut that will provide exact solutions of the quadratic equation ax2 +bx+c = 0. We start by moving the constant term to the other side of the equation.

\[\begin{array}{rlrl}{a x^{2}+b x+c} & {=0} & {} & \color{Red} {\text { Quadratic equation. }} \\ {a x^{2}+b x} & {=-c} & {} & \color{Red} {\text { Subtract } c \text { from both sides. }}\end{array} \nonumber \]

In preparation for completing the square, we next divide both sides of the equation by $a$.

\[x^{2}+\dfrac{b}{a} x=-\dfrac{c}{a} \quad \text { Divide both sides by } a \nonumber \]

Now we complete the square. Take one-half of the coeﬃcient of $x$, then square the result.

$\dfrac{1}{2} \cdot \dfrac{b}{a}=\dfrac{b}{2 a}$ when squared gives $\left(\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}$

We now add $\dfrac{b^{2}}{4 a^{2}}$ to both sides of the equation.

\[x^{2}+\dfrac{b}{a} x+\dfrac{b^{2}}{4 a^{2}}=-\dfrac{c}{a}+\dfrac{b^{2}}{4 a^{2}} \quad \color {Red} \text { Add } b^{2} /\left(4 a^{2}\right) \text { to both sides. } \nonumber \]

On the left, we factor the perfect square trinomial. On the right, we make equivalent fractions with a common denominator.

\[\begin{array}{ll}{\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{c}{a} \cdot \dfrac{4 a}{4 a}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { On the left, factor. On the right, }} \\ {} & \color {Red} {\text { create equivalent fractions with }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{4 a c}{4 a^{2}}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { Multiply numerators and denominators. }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}-4 a c}{4 a^{2}}} & \color {Red} {\text { Add fractions. }}\end{array} \nonumber \]

When we take the square root, there are two answers.

\[x+\dfrac{b}{2 a}=\pm \sqrt{\dfrac{b^{2}-4 a c}{4 a^{2}}} \quad \color {Red} \text { Two square roots. } \nonumber \]

When you take the square root of a fraction, you take the square root of both the numerator and denominator.

\[\begin{aligned} x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{\sqrt{4 a^{2}}} \\ x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Simplify: } \sqrt{4 a^{2}}=2 a \\ x &=-\dfrac{b}{2 a} \pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Subtract } b /(2 a) \text { from both sides } \end{aligned} \nonumber \]

Because both fractions have the same denominator, we can add and subtract numerators and put the answer over the common denominator.

\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]

The quadratic formula

The equation $a x^{2}+b x+c=0$ is called a quadratic equation. Its solutions are given by\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]called the quadratic formula.

Whew! Fortunately, the result is a lot easier to apply than it is to develop! Let’s try some examples.

Example $\PageIndex{1}$

Solve for $x: x^{2}-4 x-5=0$

Solution

The integer pair $1,−5$ has product $ac = −5$ and sum $b = −4$. Hence, this trinomial factors.

\[\begin{array}{r}{x^{2}-4 x-5=0} \\ {(x+1)(x-5)=0}\end{array} \nonumber \]

Now we can use the zero product property to write:

\[\begin{array}{rlrl}{x+1} & {=0} & {\text { or }} & {x-5} & {=0} \\ {x} & {=-1} & {} & {x} & {=5}\end{array} \nonumber \]

Thus, the solutions are $x =−1$ and $x = 5$. Now, let’s give the quadratic formula a try. First, we must compare our equation with the quadratic equation, then determine the values of $a$, $b$, and $c$.

\[\begin{array}{l}{a x^{2}+b x+c=0} \\ {x^{2}-4 x-5=0}\end{array} \nonumber \]

Comparing equations, we see that $a = 1$, $b = −4$, and $c = −5$. We will now plug these numbers into the quadratic formula. First, replace each occurrence of $a$, $b$, and $c$ in the quadratic formula with open parentheses.

\[\begin{aligned}
x &=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { The quadratic formula. } \\ x& = {\dfrac{-(\quad) \pm \sqrt{(\quad)^{2}-4( )( )}}{2( )} \quad \quad \color {Red} \text { Replace } a, b, \text { and } c \text { with open parentheses. }}\end{aligned} \nonumber \]

Now we can substitute: $1$ for $a$, $−4$ for $b$, and $−5$ for$c$.

\[\begin{array}{ll}{x=\dfrac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-5)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a,-4 \text { for } b} \\ {x=\dfrac{4 \pm \sqrt{16+20}}{2}} & \color {Red} {\text { Simplify. Exponent first, then }} \\ {x=\dfrac{4 \pm \sqrt{36}}{2}} & \color {Red} {\text { Add: } 16+20=36} \\ {x=\dfrac{4 \pm 6}{2}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Note that because of the “plus or minus” symbol, we have two answers.

\[\begin{array}{ll}{x=\dfrac{4-6}{2}} & \text {or} & {x=\dfrac{4+6}{2}} \\ {x=\dfrac{-2}{2}} && {x=\dfrac{10}{2}} \\ {x=-1} && {x=5}\end{array} \nonumber \]

Note that these answers match the answers found using the ac-test to factor the trinomial.

Exercise $\PageIndex{1}$

Solve for $x: x^{2}-8x+12=0$

Answer: $2$, $6$

Example $\PageIndex{2}$

Solve for $x : x^{2}=5 x+7$

Solution

The equation is nonlinear, make one side zero.

\[\begin{array}{rlrl}{x^{2}} & {=5 x+7} & {} & \color {Red} {\text { Original equation. }} \\ {x^{2}-5 x-7} & {=0} & {} & \color {Red} {\text { Nonlinear. Make one side zero. }}\end{array} \nonumber \]

Compare $x^2 −5x−7 = 0$ with $ax^2 + bx + c = 0$ and note that $a = 1$, $b = −5$, and $c = −7$. Replace each occurrence of $a$, $b$, and $c$ with open parentheses to prepare the quadratic formula for substitution.

\[\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color {Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color {Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber \]

Substitute $1$ for $a$, $−5$ for $b$, and $−7$ for $c$.

\[\begin{array}{ll}{x=\dfrac{-(-5) \pm \sqrt{(-5)^{2}-4(1)(-7)}}{2(1)}} & \color {Red} {\text { Substitute: } a=1, b=-5, c=-7} \\ {x=\dfrac{5 \pm \sqrt{25+28}}{2}} & \color {Red} {\text { Exponents and multiplication first. }} \\ {x=\dfrac{5 \pm \sqrt{53}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

Check: Use the calculator to check each solution (see Figure $\PageIndex{1}$). Note that in storing $(5-\sqrt{53}) / 2$ in $\mathbf{X}$, we must surround the numerator in parentheses.

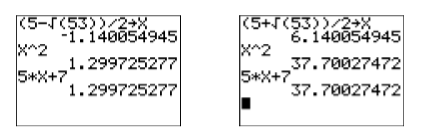
$fig 8.4.1.png$

Figure $\PageIndex{1}$: Check $(5-\sqrt{53}) / 2$ and $(5+\sqrt{53}) / 2$.

In each image in Figure $\PageIndex{1}$, after storing the solution in $\mathbf{X}$, note that the left and right-hand sides of the original equation $x^2 =5 x + 7$ produce the same number, verifying that our solutions are correct.

Exercise $\PageIndex{2}$

Solve for $x : x^{2}+7 x=10$

Answer: $(-7+\sqrt{89}) / 2,(-7-\sqrt{89}) / 2$

In addition to placing all square roots into simple radical form, sometimes you need to reduce your answer to lowest terms.

Example $\PageIndex{3}$

Solve for $x : 7 x^{2}-10 x+1=0$

Solution

Compare $7x^2 −10x + 1 = 0$ with $ax^2 + bx + c = 0$ and note that $a = 7$, $b = −10$, and $c = 1$. Replace each occurrence of $a$, $b$, and $c$ with open parentheses to prepare the quadratic formula for substitution.

\[\begin{aligned}
x &=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { The quadratic formula. } \\
x &= \dfrac{-(\quad) \pm \sqrt{( )^{2}-4( )( )}}{2( )} \quad \color {Red} \text { Replace } a, b, \text { and } c \text { with open parentheses.}
\end{aligned} \nonumber \]

Substitute $7$ for $a$, $−10$ for $b$, and $1$ for $c$.

\[\begin{array}{ll}{x=\dfrac{-(-10) \pm \sqrt{(-10)^{2}-4(7)(1)}}{2(7)}} & \color {Red} {\text { Substitute: } 7 \text { for } a} \\ {x=\dfrac{10 \pm \sqrt{100-28}}{14}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {x=\dfrac{10 \pm \sqrt{72}}{14}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

In this case, note that we can factor out a perfect square, namely $\sqrt{36}$.

\[\begin{array}{ll}{x=\dfrac{10 \pm \sqrt{36} \sqrt{2}}{14}} & \color {Red} {\sqrt{72}=\sqrt{36} \sqrt{2}} \\ {x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Finally, notice that both numerator and denominator are divisible by $2$.

\[\begin{aligned}
x&= \dfrac{\tfrac{10 \pm 6 \sqrt{2}}{2}}{\tfrac{14}{2}} \quad \color {Red} \text { Divide numerator and denominator by } 2. \\
x&= \dfrac{\tfrac{10}{2} \pm \tfrac{6 \sqrt{2}}{2}}{\tfrac{14}{2}} \quad \color {Red} \text { Distribute the } 2.\\ x&=\dfrac{5 \pm 3 \sqrt{2}}{7} \quad \color {Red} \text { Simplify. }
\end{aligned} \nonumber \]

Alternate simpliﬁcation: Rather than dividing numerator and denominator by $2$, some prefer to factor and cancel, as follows.

\[\begin{array}{ll}{x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Original answer. }} \\ {x=\dfrac{2(5 \pm 3 \sqrt{2})}{2(7)}} & \color {Red} {\text { Factor out a } 2} \\ {x=\dfrac{\not{2}(5 \pm 3 \sqrt{2})}{\not{2}(7)}} & \color {Red} {\text { Cancel. }} \\ {x=\dfrac{5 \pm 3 \sqrt{2}}{7}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

Note that we get the same answer using this technique.

Exercise $\PageIndex{3}$

Solve for $x : 3 x^{2}+8 x+2=0$

Answer: $(-4+\sqrt{10}) / 3,(-4-\sqrt{10}) / 3$

Example $\PageIndex{4}$

An object is launched vertically and its height $y$ (in feet) above ground level is given by the equation $y = 320+192t−16t^2$, wheret is the time (in seconds) that has passed since its launch. How much time must pass after the launch before the object returns to ground level? After placing the answer in simple form and reducing, use your calculator to round the answer to the nearest tenth of a second.

Solution

When the object returns to ground level, its height $y$ above ground level is $y = 0$ feet. To ﬁnd the time when this occurs, substitute $y = 0$ in the formula $y = 320 + 192t−16t^2$ and solve for $t$.

\[\begin{array}{ll}{y=320+192 t-16 t^{2}} & \color {Red} {\text { Original equation. }} \\ {0=320+192 t-16 t^{2}} & \color {Red} {\text { Set } y=0}\end{array} \nonumber \]

Each of the coeﬃcients is divisible by $−16$.

\[0=t^{2}-12 t-20 \quad \color{Red} \text { Divide both sides by }-16 \nonumber \]

Compare $t^2−12t−20 = 0$ with $at^2 +bt+c = 0$ and note that $a = 1$, $b = −12$, and $c = −20$. Replace each occurrence of $a$, $b$, and $c$ with open parentheses to prepare the quadratic formula for substitution. Note that we are solving for t this time, not $x$.

Substitute $1$ for $a$, $−12$ for $b$, and $−20$ for $c$.

\[\begin{array}{ll}{t=\dfrac{-(-12) \pm \sqrt{(-12)^{2}-4(1)(-20)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a} \\ {t=\dfrac{12 \pm \sqrt{144+80}}{2}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {t=\dfrac{12 \pm \sqrt{224}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

The answer is not in simple form, as we can factor out $\sqrt{16}$.

\[\begin{array}{ll}{t=\dfrac{12 \pm \sqrt{16} \sqrt{14}}{2}} & \color {Red} {\sqrt{224}=\sqrt{16} \sqrt{14}} \\ {t=\dfrac{12 \pm 4 \sqrt{14}}{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]

Use the distributive property to divide both terms in the numerator by $2$.

\[\begin{array}{ll}{t=\dfrac{12}{2} \pm \dfrac{4 \sqrt{14}}{2}} & \color{Red} {\text { Divide both terms by } 2} \\ {t=6 \pm 2 \sqrt{14}} & \color {Red} {\text { Simplify }}\end{array} \nonumber \]

Thus, we have two solutions, $t=6-2 \sqrt{14}$ and $t=6+2 \sqrt{14}$. Use your calculator to ﬁnd decimal approximations, then round to the nearest tenth.

$fig 8.4.2.png$

Figure $\PageIndex{2}$: Using calculator to ﬁnd decimal approximations

\[t \approx-1.5,13.5 \nonumber \]

The negative time is irrelevant, so to the nearest tenth of a second, it takes the object approximately $13.5$ seconds to return to ground level.

Exercise $\PageIndex{4}$

An object is launched vertically and its height $y$ (in feet) above ground level is given by the equation $y = 160 + 96t−16t^2$, where $t$ is the time (in seconds) that has passed since its launch. How much time must pass after the launch before the object returns to ground level?

Answer: $3+\sqrt{19} \approx 7.4$ seconds

Example $\PageIndex{5}$

Arnie gets on his bike at noon and begins to ride due north at a constant rate of $12$ miles per hour. At 1:00 PM, Barbara gets on her bike at the same starting point and begins to ride due east at a constant rate of $8$ miles per hour. At what time of the day will they be $50$ miles apart (as the crow ﬂies)? Don’t worry about simple form, just report the time of day, correct to the nearest minute.

Solution

At the moment they are $50$ miles apart, let $t$ represent the time that Arnie has been riding since noon. Because Barbara started at 1:00 PM, she has been riding for one hour less than Arnie. So, let $t−1$ represent the numbers of hours that Barbara has been riding at the moment they are $50$ miles apart.

Now, if Arnie has been riding at a constant rate of $12$ miles per hour for $t$ hours, then he has traveled a distance of $12t$ miles. Because Barbara has been riding at a constant rate of $8$ miles per hour for $t−1$ hours, she has traveled a distance of $8(t−1)$ miles.

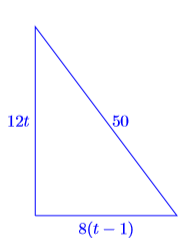
$fig 8.4.3.png$

Figure $\PageIndex{3}$: $50$ miles apart.

The distance and direction traveled by Arnie and Barbara are marked in Figure $\PageIndex{3}$. Note that we have a right triangle, so the sides of the triangle must satisfy the Pythagorean Theorem. That is,

\[(12 t)^{2}+[8(t-1)]^{2}=50^{2} \quad \color{Red} \text { Use the Pythagorean Theorem. } \nonumber \]

Distribute the $8$.

\[(12 t)^{2}+(8 t-8)^{2}=50^{2} \quad \color{Red} \text { Distribute the } 8 \nonumber \]

Square each term. Use $(a−b)^2 = a^2 −2ab + b^2$ to expand $(8t−8)^2$.

\[\begin{aligned} 144 t^{2}+64 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Square each term. } \\ 208 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Simplify: } 144 t^{2}+64 t^{2}=208 t^{2} \end{aligned} \nonumber \]

The resulting equation is nonlinear. Make one side equal to zero.

\[\begin{array}{rlrl}{208 t^{2}-128 t-2436} & {=0} & {} & \color{Red} {\text { Subtract } 2500 \text { from both sides. }} \\ {52 t^{2}-32 t-609} & {=0} & {} & \color{Red} {\text { Divide both sides by } 4 .}\end{array} \nonumber \]

Compare $52t^2 −32t−609 = 0$ with $at^2 + bt + c = 0$ and note that $a = 52$, $b = −32$, and $c = −609$. Replace each occurrence of $a$, $b$, and $c$ with open parentheses to prepare the quadratic formula for substitution. Note that we are solving for $t$ this time, not $x$.

\[\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color{Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color{Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber \]

Substitute $52$ for $a$, $−32$ for $b$, and $−609$ for $c$.

\[\begin{align*} t &= \dfrac{-(-32) \pm \sqrt{(-32)^{2}-4(52)(-609)}}{2(52)} \quad \color {Red} \text { Substitute: } 52 \text { for } a\\ t &= \dfrac{32 \pm \sqrt{1024+126672}}{104} \quad \color {Red} \text {Exponent, then multiplication.}\\ t &= \dfrac{32 \pm \sqrt{127696}}{104} \quad \color {Red} \text { Simplify. } \end{align*} \nonumber \]
Now, as the request is for an approximate time, we won’t bother with simple form and reduction, but proceed immediately to the calculator to approximate this last result (see Figure $\PageIndex{4}$). Thus, Arnie has been riding for approximately $3.743709336$ hours. To change the fractional part $0.743709336$ hours to minutes, multiply by $60$min/hr.

$fig 8.4.4.png$

Figure $\PageIndex{4}$: Approximate time that Arnie has been riding.

\[0.743709336 \mathrm{hr}=0.743709336 \mathrm{hr} \times \dfrac{60 \mathrm{min}}{\mathrm{hr}}=44.62256016 \mathrm{min} \nonumber \]

Rounding to the nearest minute, Arnie has been riding for approximately $3$ hours and $45$ minutes. Because Arnie started riding at noon, the time at which he and Barbara are $50$ miles apart is approximately 3:45 PM.

Exercise $\PageIndex{5}$

At 6:00 AM, a freight train passes through Sagebrush Junction heading west at $40$ miles per hour. At 8:00 AM, a passenger train passes through the junction heading south at $60$ miles per hour. At what time of the day, correct to the nearest minute, will the two trains be $180$ miles apart?

Answer: 9:42 AM

Search

Text Color

Text Size

Margin Size

Font Type