5.4: The Quadratic Formula
- Page ID
- 19709
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consider the general quadratic function \[f(x)=a x^{2}+b x+c \nonumber \]
In the previous section, we learned that we can find the zeros of this function by solving the equation \[f(x)=0 \nonumber \]
If we substitute \(f(x) = ax^2 + bx + c\), then the resulting equation \[a x^{2}+b x+c=0 \nonumber \]
is called a quadratic equation. In the previous section, we solved equations of this type by factoring and using the zero product property.
However, it is not always possible to factor the trinomial on the left-hand side of the quadratic equation (1) as a product of factors with integer coefficients. For example, consider the quadratic equation \[2 x^{2}+7 x-3=0 \nonumber \]
Comparing \(2x^2 + 7x − 3\) with \(ax^2 + bx + c\), let’s list all integer pairs whose product is ac = (2)(−3) = −6.

Not a single one of these integer pairs adds to b = 7. Therefore, the quadratic trinomial \(2x^2 + 7x − 3\) does not factor over the integers. Consequently, we’ll need another method to solve the quadratic equation (2).
The purpose of this section is to develop a formula that will consistently provide solutions of the general quadratic equation (1). However, before we can develop the “Quadratic Formula,” we need to lay some groundwork involving the square roots of numbers.
Square Roots
We begin our discussion of square roots by investigating the solutions of the equation \(x^2 = a\). Consider the rather simple equation
\[x^{2}=25 \nonumber \]
Because \((−5)^2 = 25\) and \((5)^2 = 25\), equation (3) has two solutions, x = −5 or x = 5. We usually denote these solutions simultaneously, using a “plus or minus” sign:
\[x=\pm 5 \nonumber \]
These solutions are called square roots of 25. Because there are two solutions, we need a different notation for each. We will denote the positive square root of 25 with the notation \(\sqrt{25}\) and the negative square root of 25 with the notation \(-\sqrt{25}\). Thus,
\[\sqrt{25}=5 \qquad \text { and } \qquad-\sqrt{25}=-5 \nonumber \]
In a similar vein, the equation \(x^{2}=36\) has two solutions, \(x=\pm \sqrt{36}\), or alternatively, \(x=\pm 6\). The notation \(\sqrt{36}\) calls for the positive square root, while the notation \(-\sqrt{36}\) calls for the negative square root. That is, \[\sqrt{36}=6 \qquad \text { and } \qquad-\sqrt{36}=-6 \nonumber \]
It is not necessary that the right-hand side of the equation \(x^2 = a\) be a “perfect square.” For example, the equation
\[x^{2}=7 \quad \text { has solutions } \quad x=\pm \sqrt{7} \nonumber \]
There is no rational square root of 7. That is, there is no way to express the square root of 7 in the form p/q, where p and q are integers. Therefore, \(\sqrt{7}\) is an example of an irrational number. However, \(\sqrt{7}\) is a perfectly valid real number and we’re perfectly comfortable leaving our answer in the form shown in equation (4).
However, if an approximation is needed for the square root of 7, we can reason that because 7 lies between 4 and 9, the square root of 7 will lie between 2 and 3. Because 7 is closer to 9 than 4, a reasonable approximation might be
\[\sqrt{7} \approx 2.6 \nonumber \]
A calculator can provide an even better approximation. For example, our TI83 reports
\[\sqrt{7} \approx 2.645751311 \nonumber \]
There are two degenerate cases involving the equation \(x^2 = a\) that demand our attention.
- The equation \(x^{2}=0\) has only one solution, namely x = 0. Thus, \(\sqrt{0} = 0\).
- The equation\(x^{2}=-4\) has no real solutions.4 It is not possible to square a real number and get −4. In this situation, we will simply state that “the equation \(x^{2}=-4\) has no real solutions (no solutions that are real numbers).”
Find all real solutions of the equations \(x^2 = 30, x^2 = 0, and x^2 = −14\).
Solution
The solutions follow.
- The equation \(x^2 = 30\) has two real solutions, namely \(x=\pm \sqrt{30}\).
- The equation \(x^2 = 0\) has one real solution, namely x = 0.
- The equation \(x^2 = -14\) has no real solutions.
Let’s try additional examples.
Find all real solutions of the equation \((x + 2)^2 = 43\).
Solution
There are two possibilities for x + 2, namely \[x+2=\pm \sqrt{43} \nonumber \]
To solve for x, subtract 2 from both sides of this last equation. \[x=-2 \pm \sqrt{43} \nonumber \]
Although this last answer is usually the preferable form of the answer, there are some times when an approximation is needed. So, our TI83 gives the following approximations.
\[-2-\sqrt{43} \approx-8.557438524 \qquad \text { and } \qquad-2+\sqrt{43} \approx 4.557438524 \nonumber \]
Find all real solutions of the equation \((x − 4)^2 = −15\).
Solution
If x is a real number, then so is x − 4. It’s not possible to square the real number x − 4 and get −15. Thus, this problem has no real solutions.
Development of the Quadratic Formula
We now have all the groundwork in place to pursue a solution of the general quadratic equation
\[a x^{2}+b x+c=0 \nonumber \]
We’re going to use a form of “completing the square” to solve this equation for x. Let’s begin by subtracting c from both sides of the equation.
\[a x^{2}+b x=-c \nonumber \]
Next, divide both sides of the equation by a. \[x^{2}+\frac{b}{a} x=-\frac{c}{a} \nonumber \]
Take half of the coefficient of x, as in (1/2)(b/a) = b/(2a). Square this result to get \(b^{2} /\left(4 a^{2}\right)\). Add this amount to both sides of the equation.
\[x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}=-\frac{c}{a}+\frac{b^{2}}{4 a^{2}} \nonumber \]
On the left we factor the perfect square trinomial. On the right we get a common denominator and add the resulting equivalent fractions.
\[\begin{array}{l}{\left(x+\frac{b}{2 a}\right)^{2}=-\frac{4 a c}{4 a^{2}}+\frac{b^{2}}{4 a^{2}}} \\ {\left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}}\end{array} \nonumber \]
Provided the right-hand side of this last equation is positive, we have two real solutions.
\[x+\frac{b}{2 a}=\pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}} \nonumber \]
On the right, we take the square root of the top and the bottom of the fraction.
\[x+\frac{b}{2 a}=\pm \frac{\sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
To complete the solution, we need only subtract b/(2a) from both sides of the equation.
\[x=-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Although this last answer is a perfectly good solution, we customarily rewrite the solution with a single common denominator.
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
This last result gives the solution to the general quadratic equation (8). The solution (9) is called the quadratic formula.
The solutions to the quadratic equation \[a x^{2}+b x+c=0 \nonumber \] are given by the quadratic formula \[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Although the development of the quadratic formula can be intimidating, in practice its application is quite simple. Let’s look at some examples.
Use the quadratic formula to solve the equation \[x^{2}=27-6 x \nonumber \]
Solution
The first step is to place the equation in the form \(ax^2 + bx + c = 0\) by moving every term to one side of the equation,7 arranging the terms in descending powers of x.
\[x^{2}+6 x-27=0 \nonumber \]
Next, compare \(x^2 + 6x − 27 = 0\) with the general form of the quadratic equation \(ax^2 + bx + c = 0\) and note that a = 1, b = 6, and c = −27. Copy down the quadratic formula.
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Substitute a = 1, b = 6, and c = −27 and simplify.
\[\begin{aligned} x &=\frac{-(6) \pm \sqrt{(6)^{2}-4(1)(-27)}}{2(1)} \\ x &=\frac{-6 \pm \sqrt{36+108}}{2} \\ x &=\frac{-6 \pm \sqrt{144}}{2} \end{aligned} \nonumber \]
In this case, 144 is a perfect square. That is, \(\sqrt{144} = 12\), so we can continue to simplify \[x=\frac{-6 \pm 12}{2} \nonumber \]
It’s important to note that there are two real answers, namely
\[x=\frac{-6-12}{2} \quad \text { or } \qquad x=\frac{-6+12}{2} \nonumber \]
Simplifying, \[x=-9 \qquad \text { or } \qquad x=3 \nonumber \]
It’s interesting to note that this problem could have been solved by factoring. Indeed,
\[\begin{aligned} x^{2}+6 x-27 &=0 \\(x-3)(x+9) &=0 \end{aligned} \nonumber \]
so the zero product property requires that either x − 3 = 0 or x + 9 = 0, which leads to x = 3 or x = −9, answers identical to those found by the quadratic formula.
We’ll have more to say about the “discriminant” soon, but it’s no coincidence that the quadratic \(x^2 + 6x − 27\) factored. Here is the relevant fact.
In the quadratic formula, \[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \] the number under the radical, \(b^2 − 4ac\), is called the discriminant. When the discriminant is a perfect square, the quadratic function will always factor.
However, it is not always the case that we can factor the given quadratic. Let’s look at another example.
Given the quadratic function \(f(x) = x^2 − 2x\), find all real solutions of f(x) = 2.
Solution
Because \(f(x) = x^2 − 2x\), the equation f(x) = 2 becomes
\[x^{2}-2 x=2 \nonumber \]
Set one side of the equation equal to zero by subtracting 2 from both sides of the equation.
\[x^{2}-2 x-2=0 \nonumber \]
Compare \(x^2 − 2x − 2 = 0\) with the general quadratic equation \(ax^2 + bx + c = 0\) and note that a = 1, b = −2 and c = −2. Write down the quadratic formula.
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Next, substitute a = 1, b = −2, and c = −2. Note the careful use of parentheses.
\[x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-2)}}{2(1)} \nonumber \]
Simplify. \[\begin{array}{l}{x=\frac{2 \pm \sqrt{4+8}}{2}} \\ {x=\frac{2 \pm \sqrt{12}}{2}}\end{array} \nonumber \]
In this case, 12 is not a perfect square, so we’ve simplified as much as is possible at this time.10 However, we can approximate these solutions with the aid of a calculator.
\[x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808 \nonumber \]
We will find these approximations useful in what follows.
The equations in Examples \(\PageIndex{4}\) and \(\PageIndex{5}\) represent a fundamental shift in our usual technique for solving equations. In the past, we’ve tried to “isolate” the terms containing x (or whatever unknown we are solving for) on one side of the equation, and all other terms on the other side of the equation. Now, in Examples \(\PageIndex{4}\) and \(\PageIndex{5}\), we find ourselves moving everything to one side of the equation, making one side of the equation equal to zero. This bears some explanation.
Let’s assume that the unknown we are solving for is x.
- If the highest power of x present in the equation is x to the first power, then the equation is linear. Thus, for example, each of the equations \[2 x+3=7, \quad 3-4 x=5 x+9, \quad \text { and } \qquad a x+b=c x+d \nonumber \] is linear.
- If there are powers of x higher than x to the first power in the equation, then the equation is nonlinear. Thus, for example, each of the equations \[x^{2}-4 x=9, \qquad x^{3}=2 x+3, \quad \text { and } \quad a x^{2}+b x=c x+d \nonumber \]is nonlinear.
The strategy for solving an equation will shift, depending on whether the equation is linear or nonlinear.
When solving equations, you must first ask if the equation is linear or nonlinear. Again, let’s assume the unknown we wish to solve for is x.
- If the equation is linear, move all terms containing x to one side of the equation, all the remaining terms to the other side of the equation.
- If the equation is nonlinear, move all terms to one side of the equation, making the other side of the equation zero.
Thus, because ax + b = cx + d is linear in x, the first step in solving the equation would be to move all terms containing x to one side of the equation, all other terms to the other side of the equation, as in
\[a x-c x=d-b \nonumber \]
On the other hand, the equation \(ax^2 + bx = cx + d\) is nonlinear in x, so the first step would be to move all terms to one side of the equation, making the other side of the equation equal to zero, as in \[a x^{2}+b x-c x-d=0 \nonumber \]
In Example \(\PageIndex{5}\), the equation \(x^2−2x = 2\) is nonlinear in x, so we moved everything to the left-hand side of the equation, making the right-hand side of the equation equal to zero, as in \(x^2 −2x−2 = 0\). However, it doesn’t matter which side you make equal to zero. Suppose instead that you move every term to the right-hand side of the equation, as in \[0=-x^{2}+2 x+2 \nonumber \]
Comparing \(0 = −x^2 + 2x + 2\) with general quadratic equation \(0 = ax^2 + bx + c\), note that a = −1, b = 2, and c = 2. Write down the quadratic formula.
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Next, substitute a = −1, b = 2, and c = 2. Again, note the careful use of parentheses.
\[x=\frac{-(2) \pm \sqrt{(2)^{2}-4(-1)(2)}}{2(-1)} \nonumber \]
This leads to two solutions, \[x=\frac{-2 \pm \sqrt{4+8}}{-2}=\frac{-2 \pm \sqrt{12}}{-2} \nonumber \]
In Example \(\PageIndex{5}\), we found the following solutions and their approximations.
\[x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808 \nonumber \]
It is a fair question to ask if our solutions \(x=(-2 \pm \sqrt{12}) /(-2)\) are the same. One way to find out is to find decimal approximations of each on our calculator.
\[x=\frac{-2-\sqrt{12}}{-2} \approx 2.732050808 \qquad x=\frac{-2+\sqrt{12}}{-2} \approx-0.7320508076 \nonumber \]
The fact that we get the same decimal approximations should spark confidence that we have the same solutions. However, we can also manipulate the exact forms of our solutions to show that they match the previous forms found in Example \(\PageIndex{5}\).
Take the two solutions and multiply both numerator and denominator by minus one.
\[\frac{-2-\sqrt{12}}{-2}=\frac{2+\sqrt{12}}{2} \qquad \text { and } \quad \frac{-2+\sqrt{12}}{-2}=\frac{2-\sqrt{12}}{2} \nonumber \]
This shows that our solutions are identical to those found in Example \(\PageIndex{5}\).
We can do the same negation of numerator and denominator in compact form.
\[\frac{-2 \pm \sqrt{12}}{-2}=\frac{2 \mp \sqrt{12}}{2} \nonumber \]
Note that this leads to the same two answers, \((2-\sqrt{12}) / 2\) and \((2+\sqrt{12}) / 2\).
Of the two methods (move all the terms to the left or all the terms to the right), we prefer the approach of Example \(\PageIndex{5}\). By moving the terms to the left-hand side of the equation, as in \(x^2 − 2x − 2 = 0\), the coefficient of \(x^2\) is positive (a = 1) and we avoid the minus sign in the denominator produced by the quadratic formula.
Intercepts
In Example \(\PageIndex{5}\), we used the quadratic formula to find the solutions of \(x^2 − 2x − 2 = 0\). These solutions, and their approximations, are shown in equation (14). It is important to make the connection that the solutions in equation (14) are the zeros of the quadratic function \(g(x) = x^2 − 2x − 2\). The zeros also provide the x-coordinates of the x-intercepts of the graph of g (a parabola). To emphasize this point, let’s draw the graph of the parabola having the equation \(g(x) = x^2 − 2x − 2\).
First, complete the square to place the quadratic function in vertex form. Take half the middle coefficient and square, as in \([(1/2)(−2)]^2 = 1\); then add and subtract this term so the equation remains balanced.
\[\begin{array}{l}{g(x)=x^{2}-2 x-2} \\ {g(x)=x^{2}-2 x+1-1-2}\end{array} \nonumber \]
Factor the perfect square trinomial, then combine the constants at the end. \[g(x)=(x-1)^{2}-3 \nonumber \]
This is a parabola that opens upward. It is shifted to the right 1 unit and down 3 units. This makes it easy to identify the vertex and draw the axis of symmetry, as shown in Figure \(\PageIndex{1}\)(a).
It will now be apparent why we used our calculator to approximate the solutions in (14). These are the x-coordinates of the x-intercepts. One x-intercept is located at approximately (−0.73, 0), the other at approximately (2.73, 0). These approximations are used to plot the location of the intercepts as shown in Figure \(\PageIndex{1}\)(b). However, the actual values of the intercepts are \(((2-\sqrt{12}) / 2,0)\) and \(((2+\sqrt{12}) / 2,0)\), and these exact values should be used to annotate the intercepts, as shown in Figure \(\PageIndex{1}\)(b).
Finally, to find the y-intercept, let x = 0 in \(g(x) = x^2 − 2x − 2\). Thus, g(0) = −2 and the y-intercept is (0, −2). The y-intercept and its mirror image across the axis of symmetry are both plotted in Figure \(\PageIndex{1}\)(c), where the final graph of the parabola is also shown.
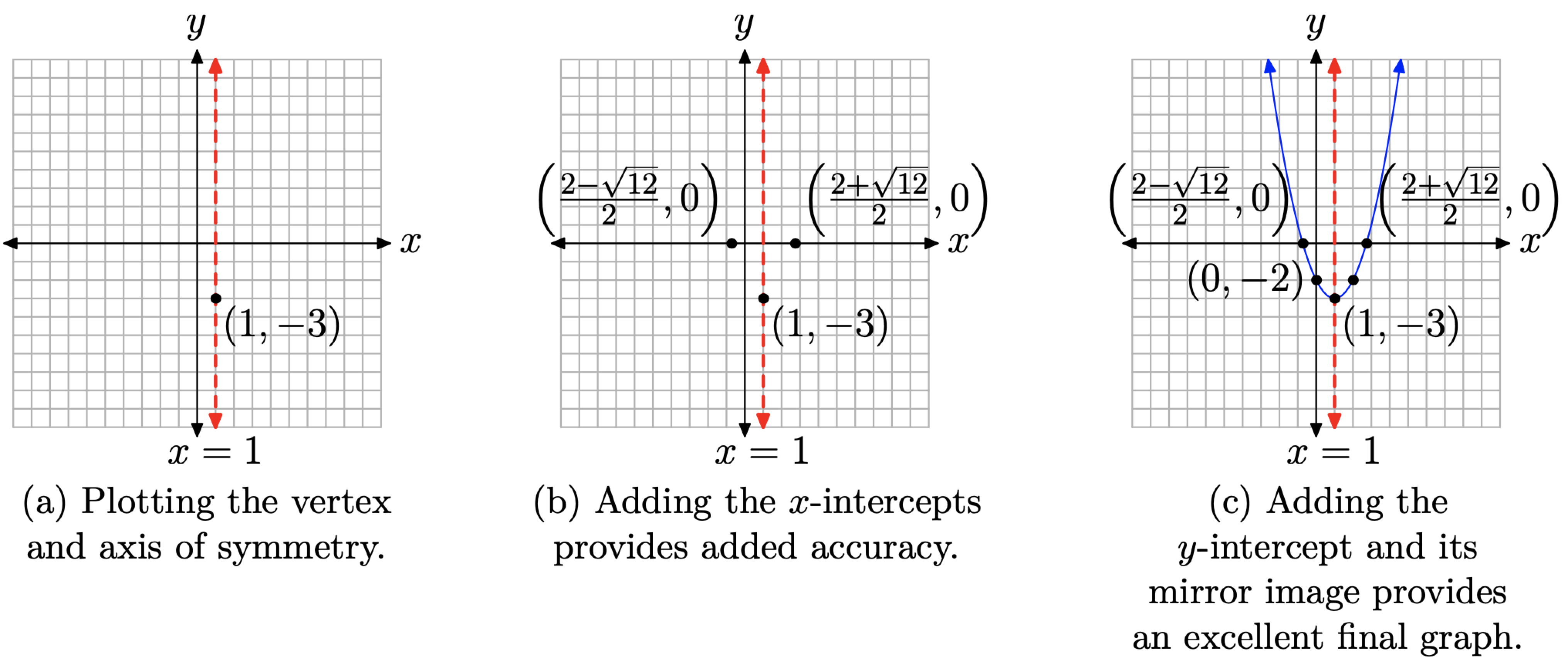
We’ve made an important point and we pause to provide emphasis.
Whenever you use the quadratic formula to solve the quadratic equation \[a x^{2}+b x+c=0 \nonumber \]
the solutions \[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
are the zeros of the quadratic function \[f(x)=a x^{2}+b x+c \nonumber \]
The solutions also provide the x-coordinates of the x-intercepts of the graph of f.
We need to discuss one final concept.
The Discriminant
Consider again the quadratic equation \(ax^2 + bx + c = 0\) and the solutions (zeros) provided by the quadratic formula
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
The expression under the radical, \(b^2 − 4ac\), is called the discriminant, which we denote by the letter D. That is, the formula for the discriminant is given by
\[D=b^{2}-4 a c \nonumber \]
The discriminant is used to determine the nature and number of solutions to the quadratic equation \(ax^2+bx+c = 0\). This is done without actually calculating the solutions.
Let’s look at three key examples.
Consider the quadratic equation \[x^{2}-4 x-4=0 \nonumber \] Calculate the discriminant and use it to determine the nature and number of the solutions.
Solution
Compare \(x^2 − 4x − 4 = 0\) with \(ax^2 + bx + c = 0\) and note that a = 1, b = −4, and c = −4. The discriminant is given by the calculation
\[D=b^{2}-4 a c=(-4)^{2}-4(1)(-4)=32 \nonumber \]
Note that the discriminant D is positive; i.e., D > 0.
Consider the quadratic function \(f(x) = x^2 − 4x − 4\), which can be written in vertex form
\[f(x)=(x-2)^{2}-8 \nonumber \]
This is a parabola that opens upward. It is shifted to the right 2 units, then downward 8 units. Therefore, it will cross the x-axis in two locations. Hence, one would expect that the quadratic formula would provide two real solutions (x-intercepts). Indeed,
\[x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-4)}}{2(1)}=\frac{4 \pm \sqrt{32}}{2} \nonumber \]
Note that the discriminant, D = 32 as calculated above, is the number under the square root. These solutions have approximations
\[x=\frac{4-\sqrt{32}}{2} \approx-0.8284271247 \qquad \text { and } \qquad x=\frac{4+\sqrt{32}}{2} \approx 4.828427125 \nonumber \]
which aid in plotting an accurate graph of \(f(x) = (x − 2)^2 − 8\), as shown in Figure \(\PageIndex{2}\).
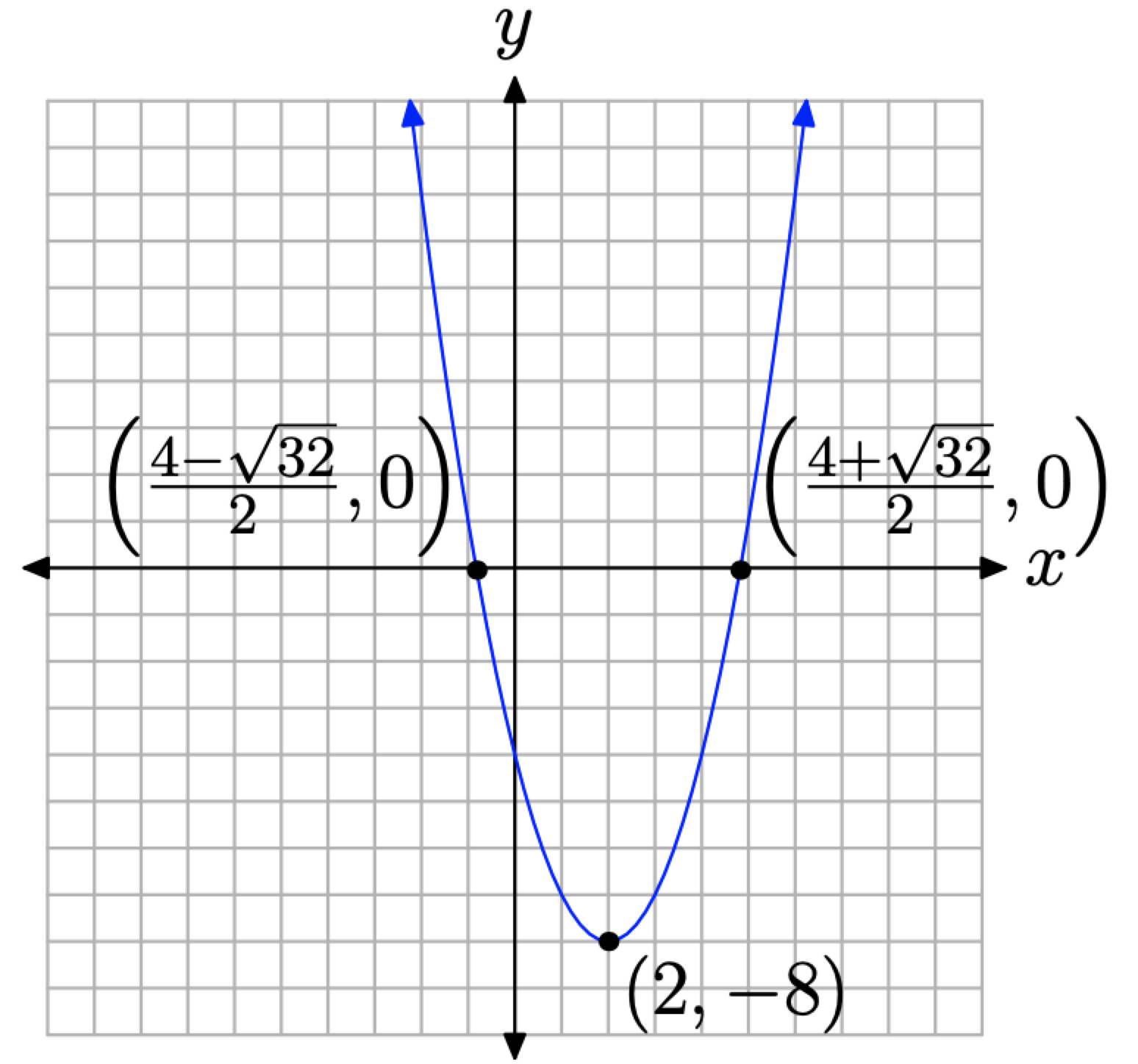
Thus, if the discriminant is positive, the parabola will have two real x-intercepts.
Next, let’s look at an example where the discriminant equals zero.
Consider again the quadratic equation \(ax^2 + bx + c = 0\) and the solutions (zeros) provided by the quadratic formula
\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \] The expression under the radical, \(b^2 − 4ac\), is called the discriminant, which we denote by the letter D. That is, the formula for the discriminant is given by \[D=b^{2}-4 a c \nonumber \]
The discriminant is used to determine the nature and number of solutions to the quadratic equation \(ax^2+bx+c = 0\). This is done without actually calculating the solutions. Consider the quadratic equation \[x^{2}-4 x+4=0 \nonumber \]
Calculate the discriminant and use it to determine the nature and number of the solutions.
Solution
Compare \(x^2 − 4x + 4 = 0\) with \(ax^2 + bx + c = 0\) and note that a = 1, b = −4, and c = 4. The discriminant is given by the calculation
\[D=b^{2}-4 a c=(-4)^{2}-4(1)(4)=0 \nonumber \]
Note that the discriminant equals zero.
Consider the quadratic function \(f(x) = x^2 − 4x + 4\), which can be written in vertex form
\[f(x)=(x-2)^{2} \nonumber \]
This is a parabola that opens upward and is shifted 2 units to the right. Note that there is no vertical shift, so the vertex of the parabola will rest on the x-axis, as shown in Figure \(\PageIndex{3}\). In this case, we found it necessary to plot two points to the right of the axis of symmetry, then mirror them across the axis of symmetry, in order to get an accurate plot of the parabola.
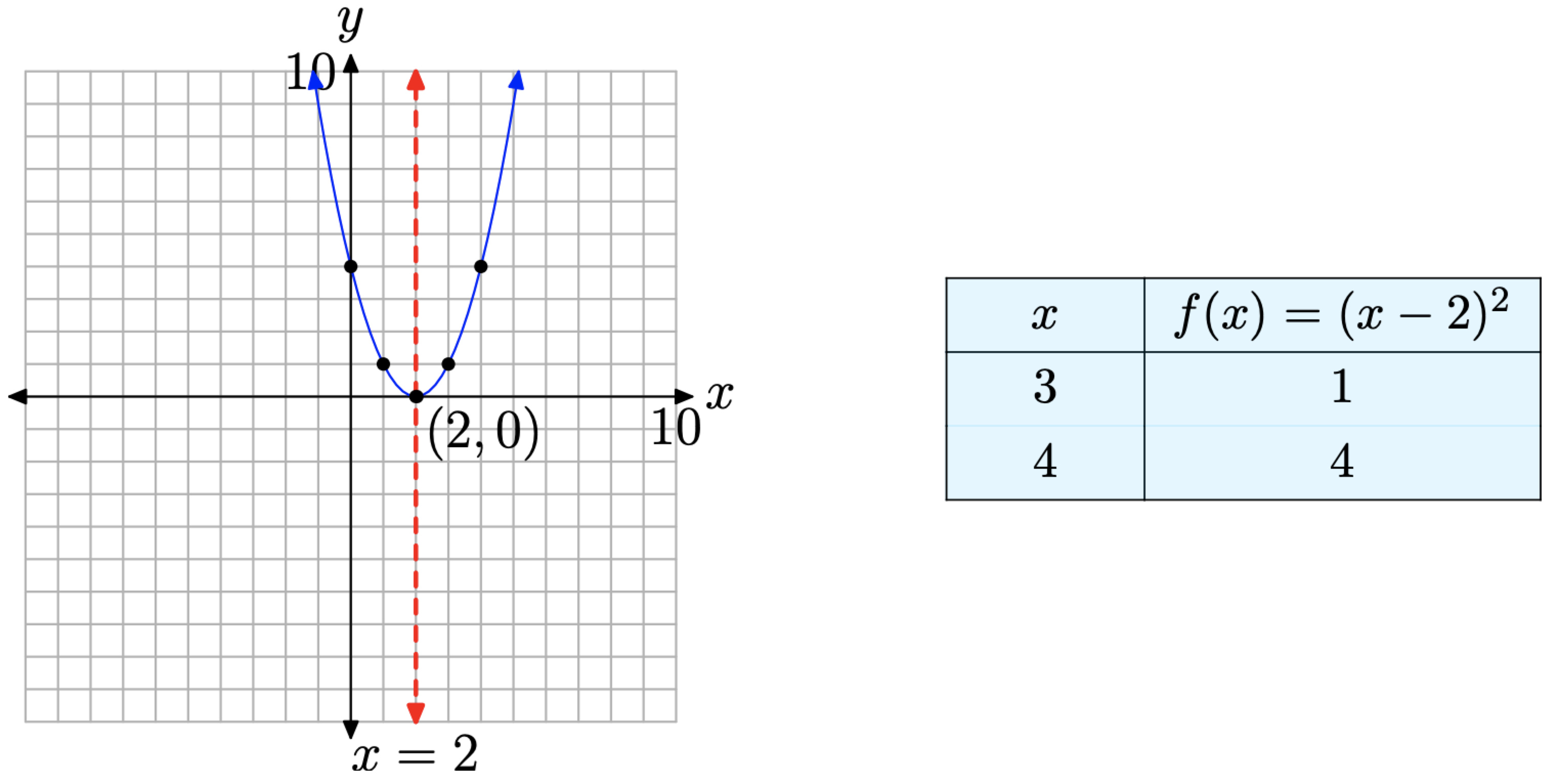
Take a closer look at equation (17). If we set f(x) = 0 in this equation, then we get \(0 = (x − 2)^2\). This could be written 0 = (x − 2)(x − 2) and we could say that the solutions are 2 and 2 again. However, mathematicians prefer to say that “2 is a solution of multiplicity 2” or “2 is a double solution.”11 Note how the parabola is tangent to the x-axis at the location of the “double solution.” That is, the parabola comes down from positive infinity, touches (but does not cross) the x-axis at x = 2, then rises again to positive infinity. Of course, the situation would be reversed in the parabola opened downward, as in \(g(x) = −(x − 2)^2\), but the graph would still “kiss” the x-axis at the location of the “double solution.”
Still, the key thing to note here is the fact that the discriminant D = 0 and the parabola has only one x-intercept. That is, the equation \(x^2 − 4x + 4 = 0\) has a single real solution.
Next, let’s look what happens when the discriminant is negative.
Consider the quadratic equation \[x^{2}-4 x+8=0 \nonumber \]
Calculate the discriminant and use it to determine the nature and number of the solutions.
Solution
Compare \(x^2 − 4x + 8 = 0\) with \(ax^2 + bx + c = 0\) and note that a = 1, b = −4, and c = 8. The discriminant is given by the calculation
\[D=b^{2}-4 a c=(-4)^{2}-4(1)(8)=-16 \nonumber \]
Note that the discriminant is negative.
Consider the quadratic function \(f(x) = x^2 − 4x + 8\), which can be written in vertex form
\[f(x)=(x-2)^{2}+4 \nonumber \]
This is a parabola that opens upward. Moreover, it has to be shifted 2 units to the right and 4 units upward, so there can be no x-intercepts, as shown in Figure \(\PageIndex{4}\). Again, we found it necessary in this example to plot two points to the right of the axis of symmetry, then mirror them, in order to get an accurate plot of the parabola.
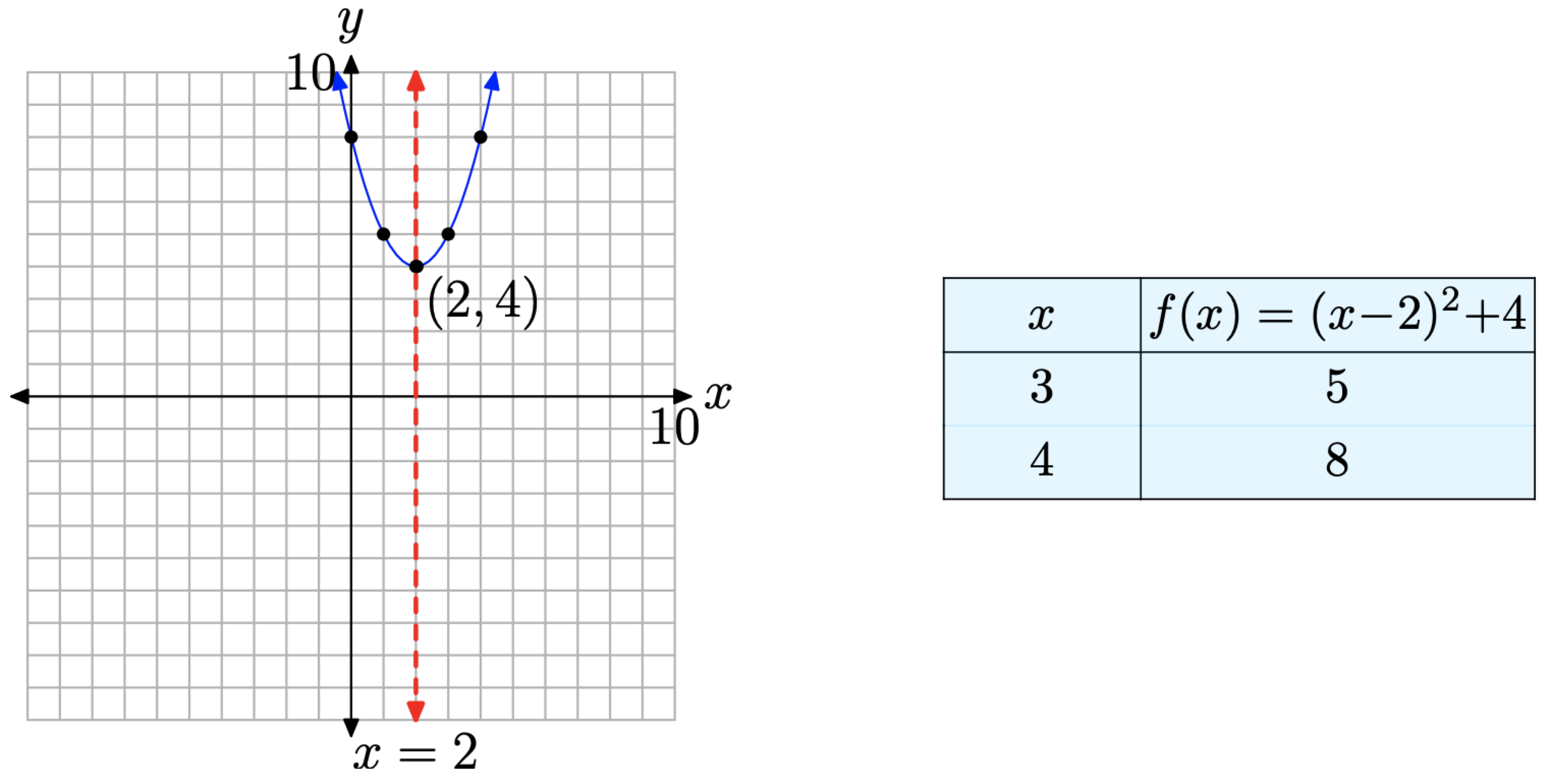
Once again, the key point in this example is the fact that the discriminant is negative and there are no real solutions of the quadratic equation (equivalently, there are no x-intercepts). Let’s see what happens if we actually try to find the solutions of \(x^2 − 4x + 8 = 0\) using the quadratic formula. Again, a = 1, b = −4, and c = 8, so \[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(8)}}{2(1)} \nonumber \] Simplifying, \[x=\frac{4 \pm \sqrt{-16}}{2} \nonumber \]
Again, remember that the number under the square root is the discriminant. In this case the discriminant is −16. It is not possible to square a real number and get −16. Thus, the quadratic equation \(x^2 − 4x + 8 = 0\) has no real solutions, as predicted.
Let’s summarize the findings in our last three examples.
Consider the quadratic equation \[a x^{2}+b x+c=0 \nonumber \]. The discriminant is defined as \[D=b^{2}-4 a c \nonumber \].
There are three possibilities:
- If D > 0, then the quadratic equation has two real solutions.
- If D = 0, then the quadratic equation has one real solution.
- If D < 0, then the quadratic equation has no real solutions.
This key result is reflected in the graph of the quadratic function.
Consider the quadratic function \[f(x)=a x^{2}+b x+c \nonumber \].
The graph of this function is a parabola. Three possibilities exist depending upon the value of the discriminant \(D = b^2 − 4ac\).
- If D > 0, the parabola has two x-intercepts.
- If D = 0, the parabola has exactly one x-intercept.
- If D < 0, the parabola has no x-intercepts.
Exercise
In Exercises 1-8, find all real solutions of the given equation. Use a calculator to approximate the answers, correct to the nearest hundredth (two decimal places).
\(x^2 = 36\)
- Answer
-
\(x = \pm 6\)
\(x^2 = 81\)
\(x^2 = 17\)
- Answer
-
\(x = \pm \sqrt{17} \approx \pm 4.12\)
\(x^2 = 13\)
\(x^2 = 0\)
- Answer
-
x = 0
\(x^2 = −18\)
\(x^2 = −12\)
- Answer
-
No real solution
\(x^2 = 3\)
In Exercises 9-16, find all real solutions of the given equation. Use a calculator to approximate your answers to the nearest hundredth.
\((x−1)^2 = 25\)
- Answer
-
x = −4 or x = 6
\((x+3)^2 = 9\)
\((x+2)^2 = 0\)
- Answer
-
x = −2
\((x−3)^2 = −9\)
\((x+6)^2 = −81\)
- Answer
-
No real solution
\((x+7)^2 = 10\)
\((x−8)^2 = 15\)
- Answer
- \(x = 8 \pm \sqrt{15} \approx 4.13, 11.87\)
\((x+10)^2 = 37\)
In Exercises 17-28, perform each of the following tasks for the given quadratic function.
- Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Remember to draw all lines with a ruler.
- Place the quadratic function in vertex form. Plot the vertex on your coordinate system and label it with its coordinates. Draw the axis of symmetry on your coordinate system and label it with its equation.
- Use the quadratic formula to find the x-intercepts of the parabola. Use a calculator to approximate each intercept, correct to the nearest tenth, and use these approximations to plot the x-intercepts on your coordinate system. However, label each x-intercept with its exact coordinates.
- Plot the y-intercept on your coordinate system and its mirror image across the axis of symmetry and label each with their coordinates.
- Using all of the information on your coordinate system, draw the graph of the parabola, then label it with the vertex form of the function. Use interval notation to state the domain and range of the quadratic function.
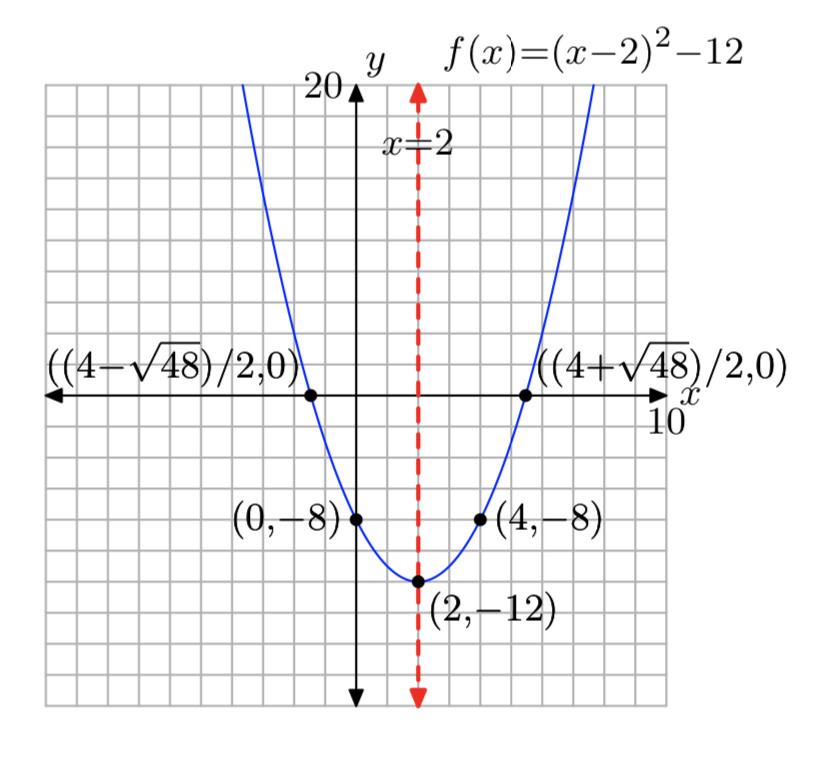
\(f(x) = x^2−4x−8\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = [−12, \(\infty\))
\(f(x) = x^2+6x−1\)
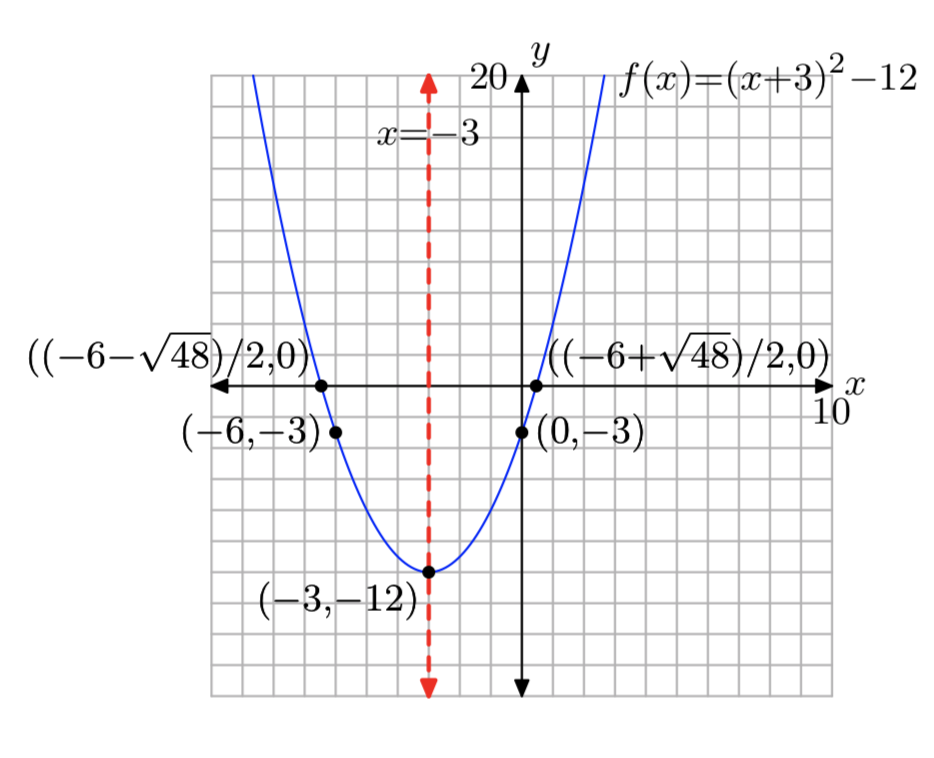
\(f(x) = x^2+6x−3\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = [−12, \(\infty\))
\(f(x) = x^2−8x+1\)
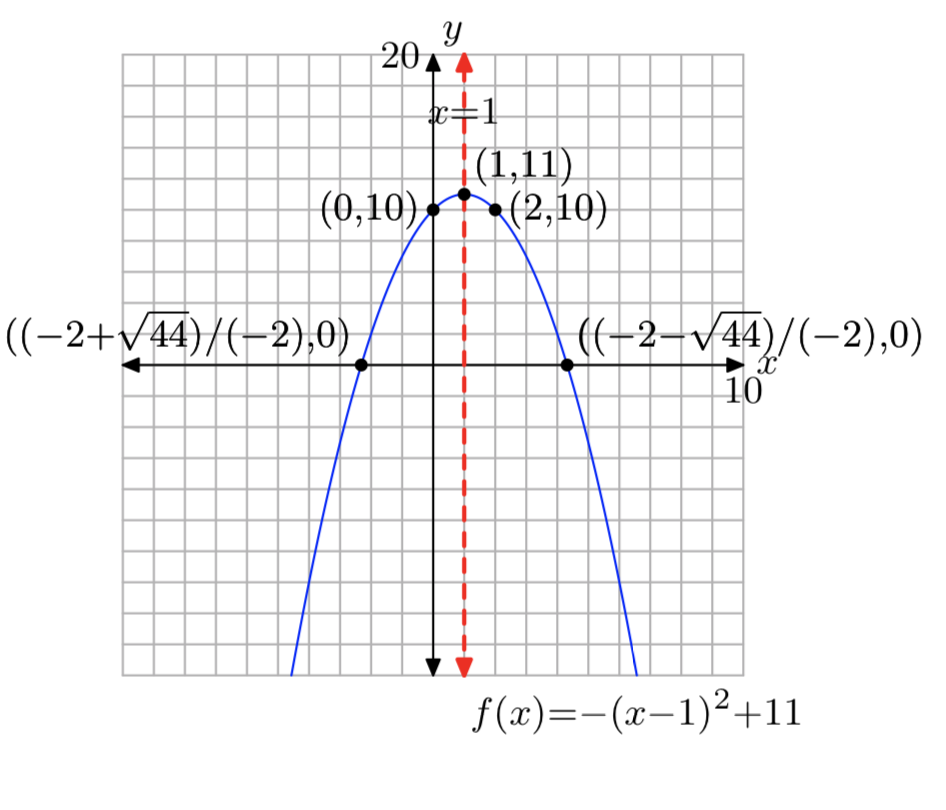
\(f(x) = −x^2+2x+10\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = (−\(\infty\), 11]
\(f(x) = −x^2−8x−8\)
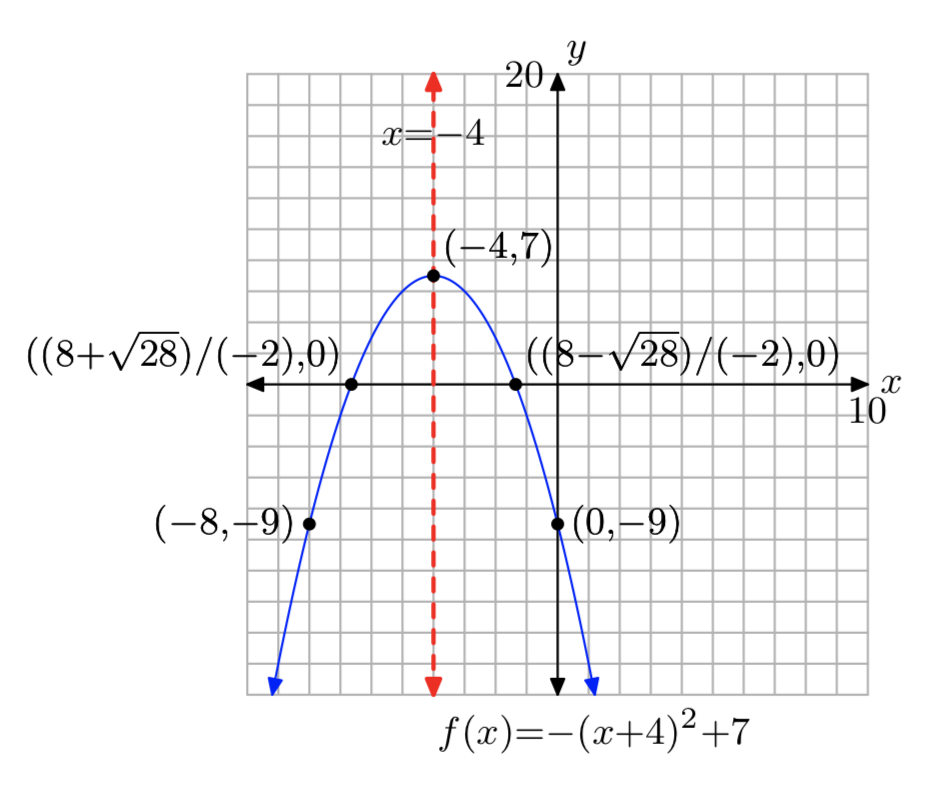
\(f(x) = −x^2−8x−9\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = (−\(\infty\), 7]
\(f(x) = −x^2+10x−20\)
\(f(x)=2x^2−20x+40\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = [−10, \(\infty\))
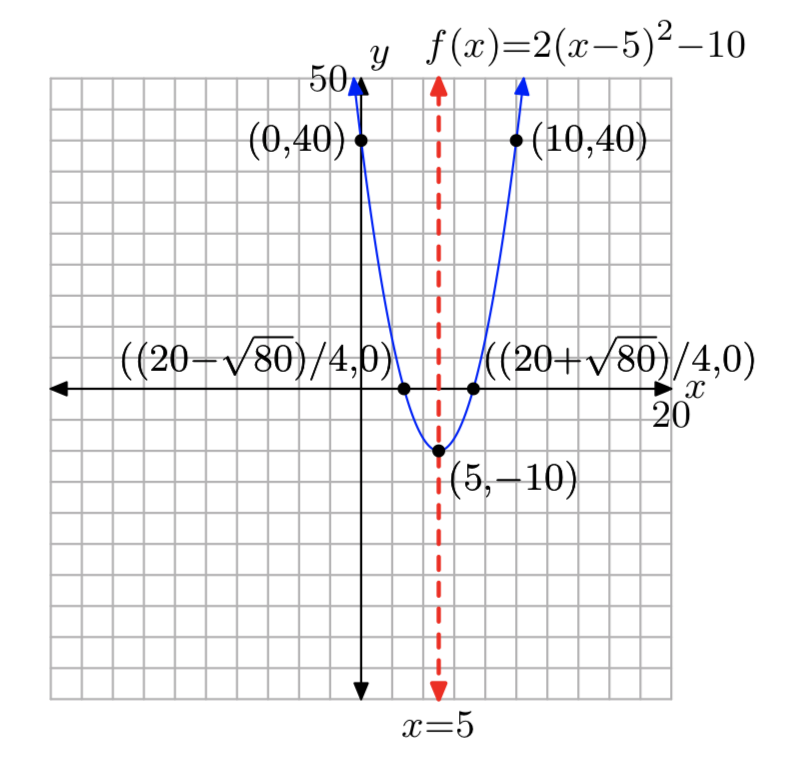
\(f(x) = 2x^2−16x+12\)
\(f(x) = −2x^2+16x+8\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = (−\(\infty\), 40]
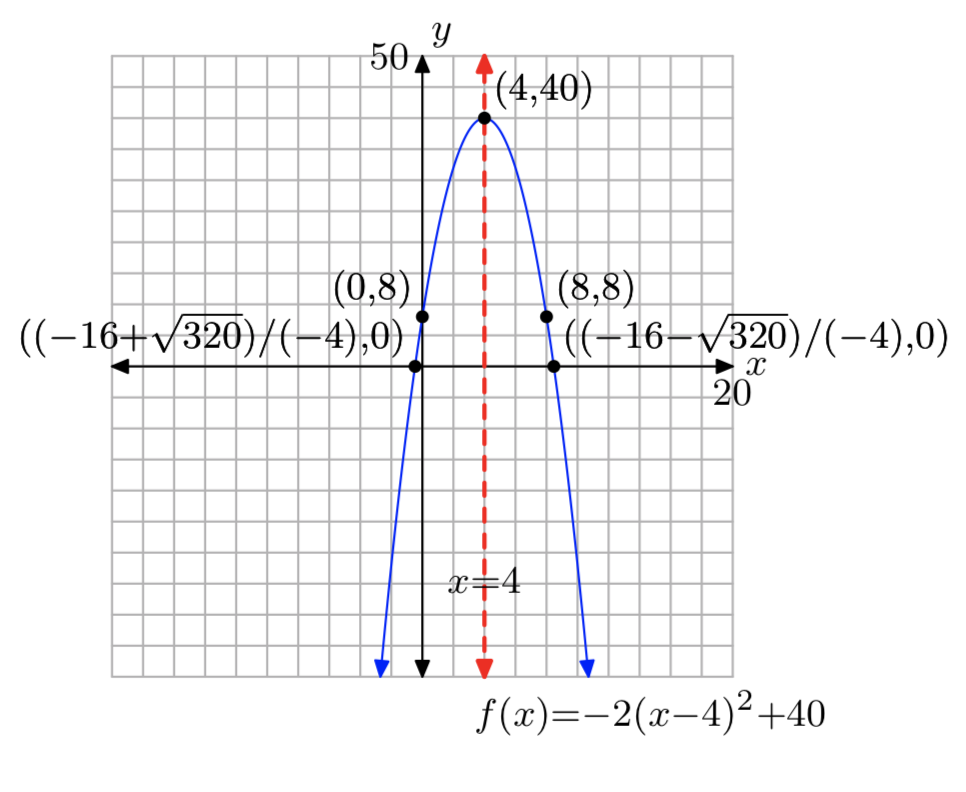
\(f(x) = −2x^2−24x−52\)
In Exercises 29-32, perform each of the following tasks for the given quadratic equation.
- Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Remember to draw all lines with a ruler.
- Show that the discriminant is negative.
- Use the technique of completing the square to put the quadratic function in vertex form. Plot the vertex on your coordinate system and label it with its coordinates. Draw the axis of symmetry on your coordinate system and label it with its equation.
- Plot the y-intercept and its mirror image across the axis of symmetry on your coordinate system and label each with their coordinates.
- Because the discriminant is negative (did you remember to show that?), there are no x-intercepts. Use the given equation to calculate one additional point, then plot the point and its mirror image across the axis of symmetry and label each with their coordinates.
- Using all of the information on your coordinate system, draw the graph of the parabola, then label it with the vertex form of function. Use interval notation to describe the domain and range of the quadratic function.
\(f(x) = x^2+4x+8\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = [4, \(\infty\))
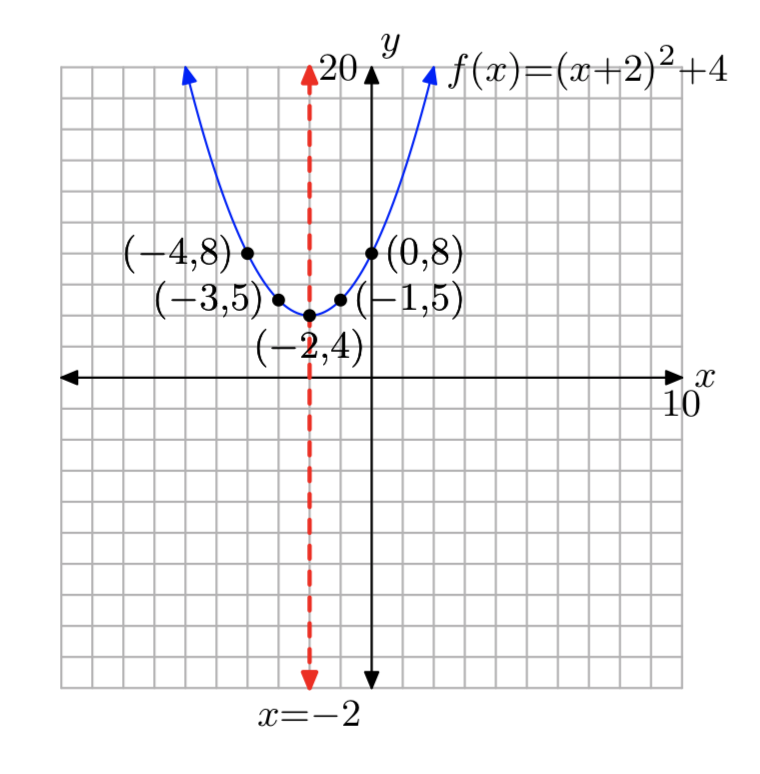
\(f(x) = x^2−4x+9\)
\(f(x) = −x^2+6x−11\)
- Answer
-
Domain = \((−\infty, \infty)\),
Range = (−\(\infty\), −2]
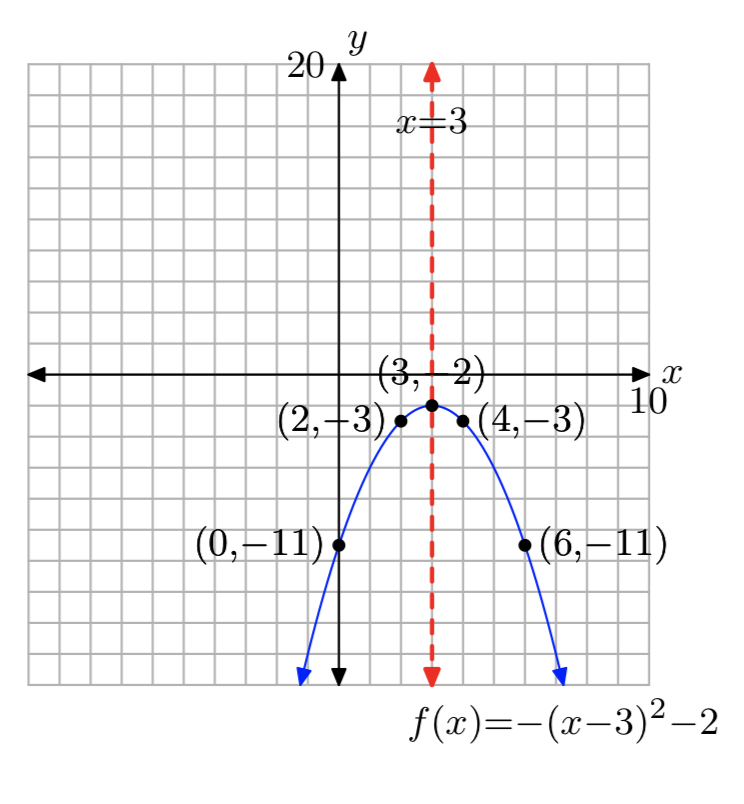
\(f(x) = −x^2−8x−20\)
In Exercises 33-36, perform each of the following tasks for the given quadratic function.
- Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Remember to draw all lines with a ruler.
- Use the discriminant to help determine the value of k so that the graph of the given quadratic function has exactly one x-intercept.
- Substitute this value of k back into the given quadratic function, then use the technique of completing the square to put the quadratic function in vertex form. Plot the vertex on your coordinate system and label it with its coordinates. Draw the axis of symmetry on your coordinate system and label it with its equation
- Plot the y-intercept and its mirror image across the axis of symmetry and label each with their coordinates.
- Use the equation to calculate an additional point on either side of the axis of symmetry, then plot this point and its mirror image across the axis of symmetry and label each with their coordinates.
- Using all of the information on your coordinate system, draw the graph of the parabola, then label it with the vertex form of the function. Use interval notation to describe the domain and range of the quadratic function.
\(f(x) = x^2−4x+4k\)
- Answer
-
k = 1
Domain = \((−\infty, \infty)\),
Range = [0, \(\infty\))
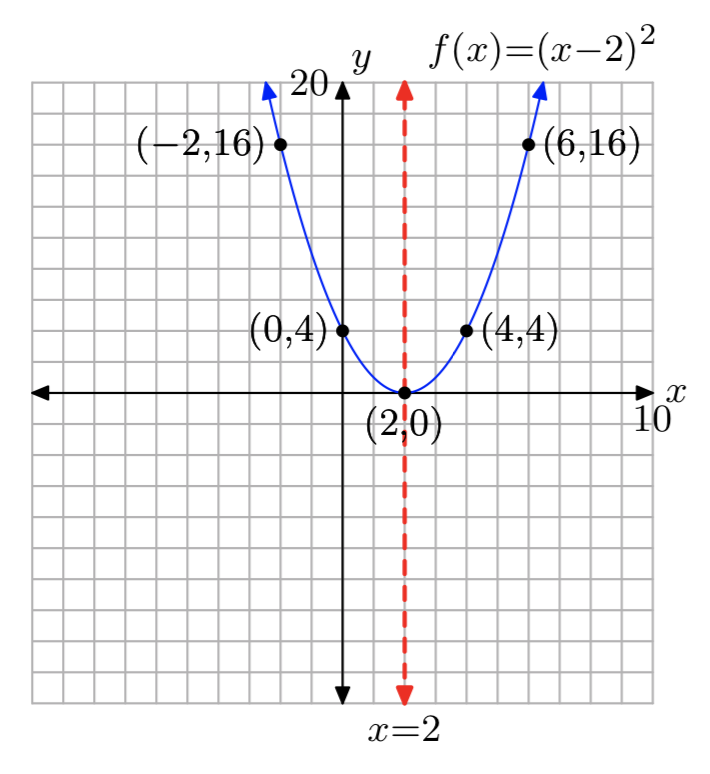
\(f(x) = x^2+6x+3k\)
\(f(x) = kx^2−16x−32\)
- Answer
-
k = −2
Domain = \((−\infty, \infty)\),
Range = (−\(\infty\), 0]
\(f(x) = kx^2−24x+48\)
Find all values of k so that the graph of the quadratic function \(f(x) = kx^2−3x+5\) has exactly two x-intercepts.
- Answer
-
{k: \(k < \frac{9}{20}\)}
Find all values of k so that the graph of the quadratic function \(f(x) = 2x^2+7x−4k\) has exactly two x-intercepts.
Find all values of k so that the graph of the quadratic function \(f(x) = 2x^2−x+5k\) has no x-intercepts.
- Answer
-
{k: \(k > \frac{1}{40}\)}
Find all values of k so that the graph of the quadratic function \(f(x) = kx^2−2x−4\) has no x-intercepts.
In Exercises 41-50, find all real solutions, if any, of the equation f(x) = b.
\(f(x) = 63x^2+74x−1\); b = 8
- Answer
-
\(−\frac{9}{7}, \frac{1}{9}\)
\(f(x) = 64x^2+128x+64\); b = 0
\(f(x) = x^2−x−5\); b = 2
- Answer
-
\(\frac{1+\sqrt{29}}{2}, \frac{1−\sqrt{29}}{2}\)
\(f(x) = 5x^2−5x\); b = 3
\(f(x) = 4x^2+4x−1\); b = −2
- Answer
-
\(−\frac{1}{2}\)
\(f(x) = 2x^2−9x−3\); b = −1
\(f(x) = 2x^2+4x+6\); b = 0
- Answer
-
no real solutions
\(f(x) = 24x^2−54x+27\); b = 0
\(f(x) = −3x^2+2x−13\); b = −5
- Answer
-
no real solutions
\(f(x) = x^2−5x−7\); b = 0
In Exercises 51-60, find all real solutions, if any, of the quadratic equation.
\(−2x^2+7 = −3x\)
- Answer
-
\(\frac{3−\sqrt{65}}{4}, \frac{3+\sqrt{65}}{4}\)
\(−x^2 = −9x+7\)
\(x^2−2 = −3x\)
- Answer
-
\(−\frac{3−\sqrt{17}}{2}, −\frac{3+\sqrt{17}}{2}\)
\(81x^2 = −162x−81\)
\(9x^2+81 = −54x\)
- Answer
-
−3
\(−30x^2−28 = −62x\)
\(−x^2+6 = 7x\)
- Answer
-
\(−\frac{7+\sqrt{73}}{2}, −\frac{7−\sqrt{73}}{2}\)
\(−8x^2 = 4x+2\)
\(4x^2+3 = −x\)
- Answer
-
no real solutions
\(27x^2 = −66x+16\)
In Exercises 61-66, find all of the x-intercepts, if any, of the given function.
\(f(x) = −4x^2−4x−5\)
- Answer
-
no x-intercepts
\(f(x) = 49x^2−28x+4\)
\(f(x) = −56x^2+47x+18\)
- Answer
-
(\(\frac{9}{8}\), 0), (\(−\frac{2}{7}\), 0)
\(f(x) = 24x^2+34x+12\)
\(f(x) = 36x^2+96x+64\)
- Answer
-
(\(−\frac{4}{3}\), 0)
\(f(x) = 5x^2+2x+3\)
In Exercises 67-74, determine the number of real solutions of the equation.
\(9x^2+6x+1 = 0\)
- Answer
-
1
\(7x^2−12x+7 = 0\)
\(−6x^2+4x−7 = 0\)
- Answer
-
0
\(−8x^2+11x−4 = 0\)
\(−5x^2−10x−5 = 0\)
- Answer
-
1
\(6x^2+11x+2 = 0\)
\(−7x^2−4x+5 = 0\)
- Answer
-
2
\(6x^2+10x+4 = 0\)


