5.5: Motion

If a particle moves with uniform or constant acceleration, then it must behave according to certain standard laws of kinematics. In this section we will develop these laws of motion and apply them to a number of interesting applications.

Uniform Speed

If an object travels with uniform (constant) speed v, then the distance d traveled in time t is given by the formula

\[d=v t \nonumber \]

or in words, “distance equals speed times time.” This concept is probably familiar to those of us who drive our cars on the highway. For example, if I drive my car at a constant speed of 50 miles per hour, in 3 hours I will travel 150 miles. That is,

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h} \nonumber \]

Note that this computation has the form “distance equals speed times time.” It is important to note how the units balance on each side of this result. This is easily seen by canceling units much as you would cancel numbers with ordinary fractions.

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\not{h}} \times 3 \not{h} \nonumber \]

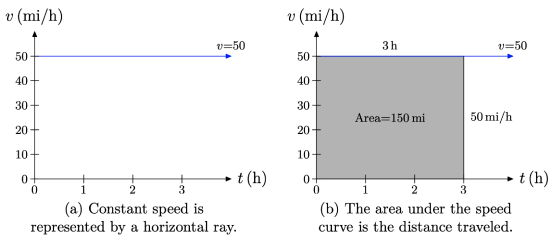
In Figure \(\PageIndex{1}\)(a) we’ve plotted the speed v of the car versus time t. Because the speed is uniform (constant), the graph is a horizontal ray, starting at time t = 0 and moving to the right. In Figure \(\PageIndex{1}\)(b), we’ve shaded the area under the constant speed ray over the time interval [0, 3] hours. Note that the area of the shaded rectangular region has height equal to 50 miles per hour (50 mi/h) and width equal to 3 hours (3 h), so the area of this rectangle is

\[\text { Area }=\text { height } \times \text { width }=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h}=150 \mathrm{mi} \nonumber \]

Note the units on the answer. The area under the constant speed ray is 150 miles. That is, the area under the speed curve is the distance traveled!

Our work has led us to the following result.

Uniform Speed

Suppose that an object travels with uniform (constant) speed v.

• The distance traveled d is given by the formula d = vt, where t is the time of travel.
• The graph of speed v versus time t will be a horizontal ray, starting at time t = 0 and moving to the right.
• The area of the rectangular region under the graph of v over the time interval [0, t] gives the distance traveled during that time period.

Figure \(\PageIndex{1}\)

Let’s look at another example.

Example \(\PageIndex{1}\)

An object is traveling with uniform speed v. The graph of v versus t is shown in the graph that follows.

Figure \(\PageIndex{2}\). The graph of the speed of the object versus time.

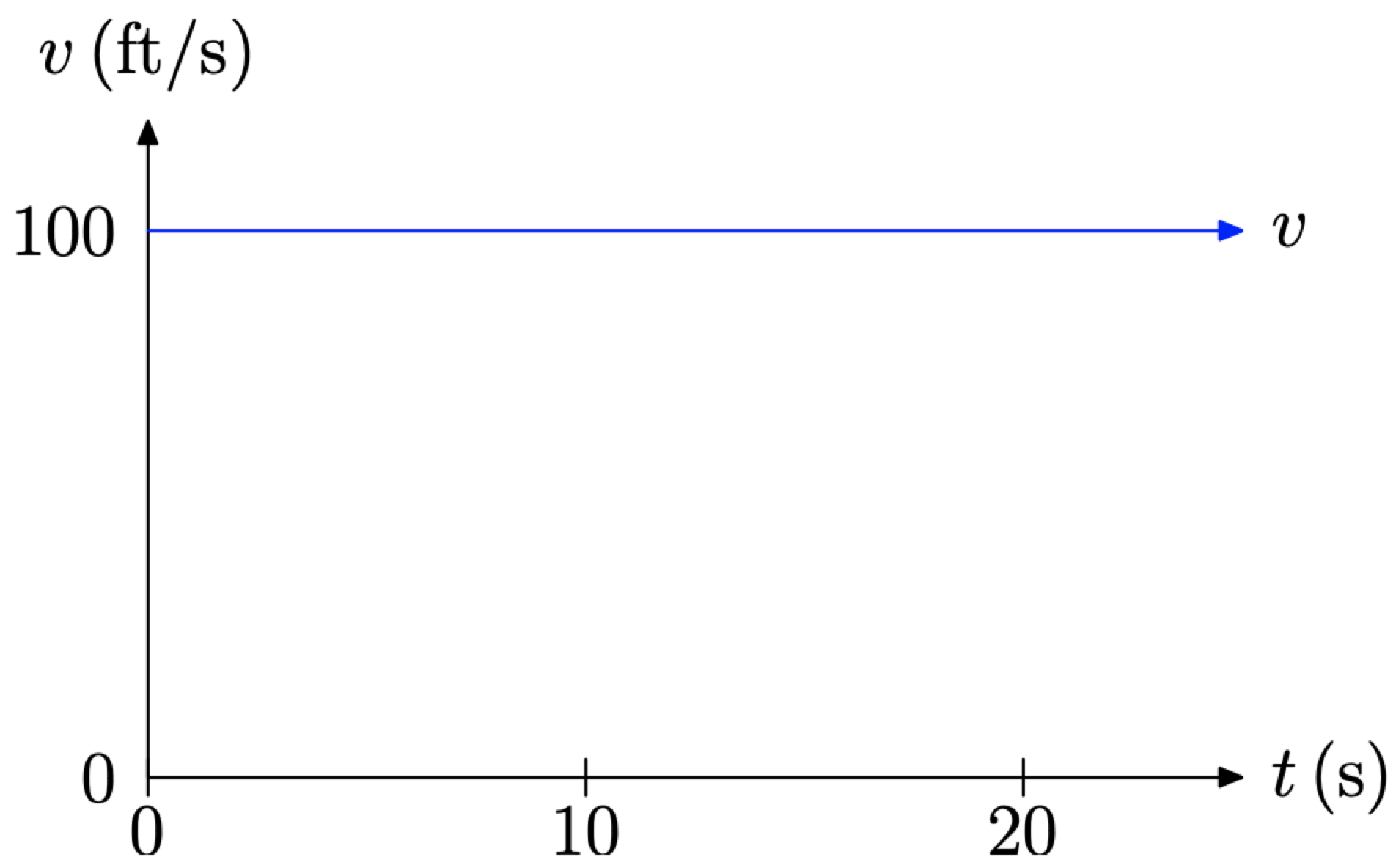
What is the speed of the object at any time t? How far will the object travel in 20 seconds?

Solution

We read the speed from the graph. Note that the ray representing the speed is level (constant) at 100 feet per second (100 ft/s). Therefore, the speed at any time t is v = 100. In function notation, we would write v(t) = 100, being mindful that the units are feet per second (ft/s).

To find the distance traveled in 20 seconds, we have two choices:

1. If we use the formula d = vt, then

\[\begin{aligned} d &=v t \\ d &=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s} \\ d &=2000 \mathrm{ft} \end{aligned} \nonumber \]

That is, the object travels 2000 feet in the 20 seconds.

2. We can also find the distance traveled by shading the area under the uniform speed curve over the 20 second time interval.

Figure \(\PageIndex{3}\). The area under the uniform speed curve represents the distance traveled.

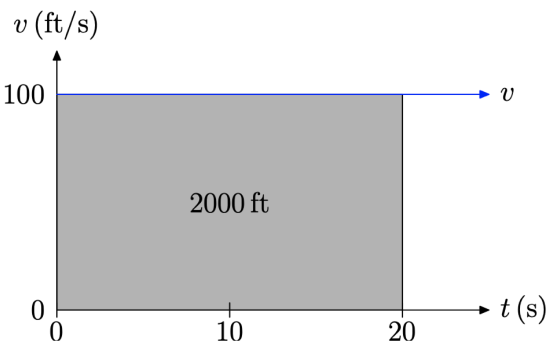
Note that the height of the shaded rectangular region in Figure \(\PageIndex{3}\) is 100 feet per second (100 ft/s) and the width is 20 seconds (20 s). Hence, the area of the shaded rectangular region is

\[\text { Area }=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s}=2000 \mathrm{ft} \nonumber \]

which is identical to the result found with the formula d = vt.

Uniform Acceleration

Let’s get back in the car again and drive down the highway at a steady (constant) speed of v = 30 miles per hour. We decide to overtake a truck in front of us, so we step on the accelerator of the car, which increases the speed of the car, allowing us to pass the truck.

Definition

Acceleration is the rate at which an object’s speed is changing with respect to time.

For example, suppose that when we step on the accelerator of the car, the speed of the car changes at a constant 20 miles per hour per hour. We would then say that the acceleration is uniform (constant) and would write

\[\text { Acceleration }=20 \frac{\mathrm{mi} / \mathrm{h}}{\mathrm{h}} \nonumber \]

or, more succinctly, as

\[\text { Acceleration }=20 \frac{\mathrm{mi}}{\mathrm{h}^{2}} \nonumber \]

The latter notation is preferred by scientists, but the notation a = 20 (mi/h)/h is much easier to understand. That is, the speed is increasing at a constant rate of 20 miles per hour every hour.

• At the moment we step on the accelerator to pass the truck, the initial speed of the car is v = 30 miles per hour. If we maintain a constant acceleration of 20 miles per hour per hour, after 1 hour, the speed increases by 20 miles per hour, so the speed of the car at the end of 1 hour is \[v=30+20(1) \nonumber \] or v = 50 miles per hour.
• At the end of two hours, the speed of the car is \[v=30+20(2) \nonumber \] or v = 70 miles per hour.
• At the end of three hours, the speed of the car is \[v = 30 + 20(3) \nonumber \], or v = 90 miles per hour.

Continuing in this manner, it’s easy to see that the speed of the car at the end of t hours will be given by the formula \[v=30+20 t \nonumber \]

It’s important to note that we are making an assumption that we keep our foot on that accelerator to maintain a uniform (constant) acceleration of 20 miles per hour per hour. Granted, this is a pretty silly example with very low acceleration (is that Fred Flintstone’s car?), but it does allow us to concentrate on the concept without having to deal with messy units.

If we follow the argument above, it’s not hard to develop the first equation of motion.

First Equation of Motion

If an object having initial speed \(v_{0}\) experiences a constant acceleration a, then its speed at time t is given by the formula \[v=v_{0}+a t \nonumber \].

We follow the scientific practice of denoting the initial speed by v0, the speed at time t = 0. That’s why we subscript v with zero.

Of course, the first equation of motion is valid only if each quantity possesses the proper units.

Example \(\PageIndex{2}\)

Suppose that a particle has an initial speed of 20 feet per second (20 ft/s) and is given a constant acceleration of 4 feet per second per second \(\left(4 f t / s^{2}\right)\). What will be the speed of the particle after 3 minutes (3 min)?

Solution

It is tempting to start with the formula \[v=v_{0}+a t \nonumber \]

and substitute \(v_{0}=20 \mathrm{ft} / \mathrm{s}, a=4 \mathrm{ft} / \mathrm{s}^{2},\) and \(t=3 \mathrm{min}\)

\[v=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft}}{\mathrm{s}^{2}} \times 3 \mathrm{min} \nonumber \]

However, note that the units will not cancel because the time is measured in minutes. What we need to do is change the time to seconds with the conversion

\[t=3 \not{min} \times 60 \frac{\mathrm{s}}{\not{min}}=180 \mathrm{s} \nonumber \]

Now the units should be correct. We substitute the time in seconds into the formula \(v = v_{0} + at\) and obtain

\[\begin{aligned} v &=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft} / \mathrm{s}}{\not{s}} \times 180 \not{\mathrm{s}} \\ &=20 \frac{\mathrm{ft}}{\mathrm{s}}+720 \frac{\mathrm{ft}}{\mathrm{s}} \\ &=740 \frac{\mathrm{ft}}{\mathrm{s}} \end{aligned} \nonumber \]

Hence, the speed of the particle at three minutes is v = 740 ft/s.

Let’s look at another example.

Example \(\PageIndex{3}\)

A ball is thrown into the air with an initial velocity of 180 feet per second (180 ft/s). It immediately begins to decelerate at a constant rate of 32 feet per second per second \((32 ft/s^2 )\). At what time will the ball reach its maximum height?

Solution

When the ball reaches its maximum height, its velocity will equal zero. That is, at the exact moment when the ball is at its maximum height, it will stop before it returns to the ground. Thus, to find the time when the ball is at its maximum height, substitute v = 0 in the formula \(v = v_{0} + at\) and solve for t.

\[\begin{aligned} 0 &=v_{0}+a t \\ a t &=-v_{0} \\ t &=-\frac{v_{0}}{a} \end{aligned} \nonumber \]

When we say that the ball decelerates at a constant rate of 32 ft/s every second, we are implying that the ball loses speed at a rate of 32 ft/s every second. Thus, the acceleration is negative in this case and we write \(a = −32 ft/s^2\).

Finally, we need only substitute the initial speed (v0 = 180 ft/s) and the acceleration \((a = −32 ft/s^2)\) into equation (6) and simplify.

\[t=-\frac{180 \mathrm{ft} / \mathrm{s}}{-32 \mathrm{ft} / \mathrm{s}^{2}} \nonumber \]

An analysis of the units is a good check that we are doing things correctly. Note that \[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s} \nonumber \]

Thus, the time for the ball to reach its maximum height is \[t = 5 s \nonumber \].

Area is Distance Traveled

If we plot the graph of the speed v versus the time t, note that the equation \(v = v_{0} +at\) has the form y = mx+b, particularly if we arrange the equation in the order \(v = at+v_{0}\). It is then easily seen that the graph will be a line with intercept equaling the initial velocity \(v_{0}\) and slope equaling the acceleration a. The graph of \(v = v_{0} + at\) is shown in Figure \(\PageIndex{4}\)(a).

In Figure \(\PageIndex{4}\)(b), we’ve shaded the area under the graph of \(v = v_{0} + at\) over the time interval [0, t]. There is a natural question to ask. Will the area under the graph of \(v = v_{0} + at\) in Figure \(\PageIndex{4}\)(b) represent the distance traveled during the time interval [0, t]?

Figure \(\PageIndex{4}\). The graph of \(v = v_{0} + at\) is a line with intercept v0 and slope a.

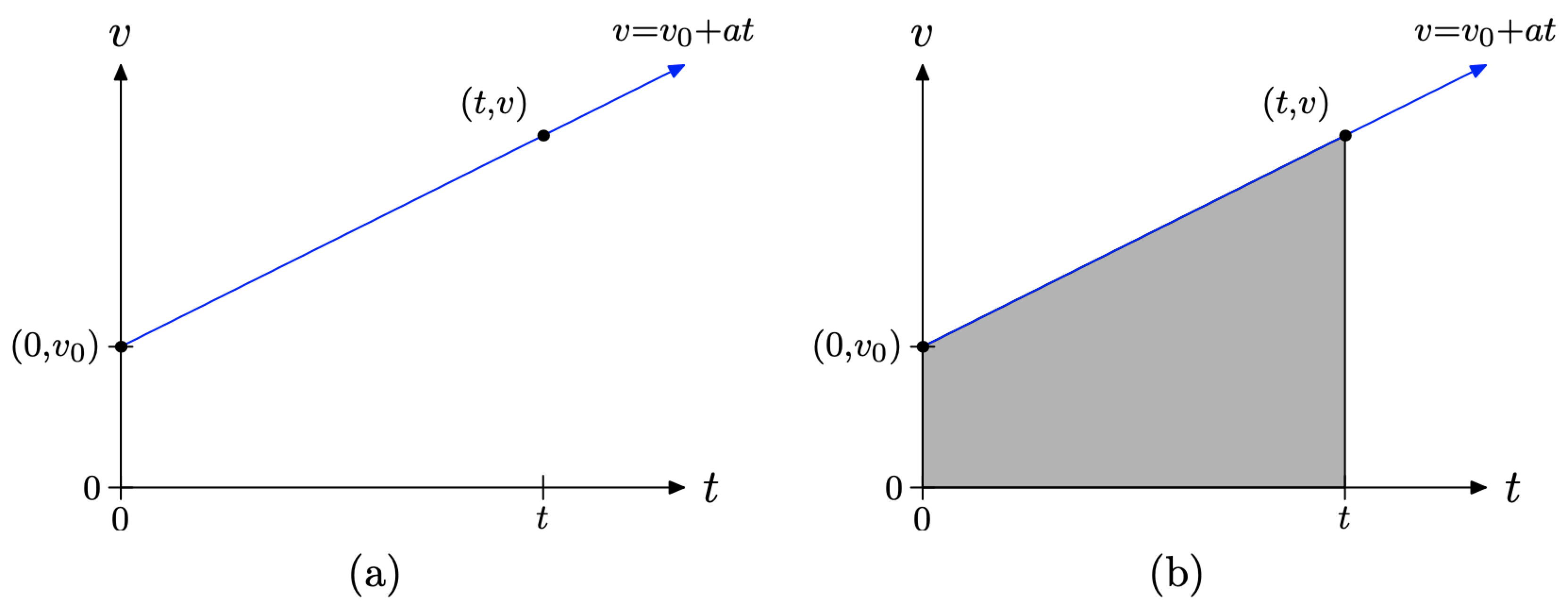
We know the area under a uniform (constant) speed ray will equal the distance traveled. Can we use this fact to answer our question on the shaded triangular region in Figure \(\PageIndex{4}\)(b)?

Let’s take the time interval [0, t] in Figure \(\PageIndex{4}\)(b) and divide it up into 4 equal subintervals of time, as shown in Figure \(\PageIndex{5}\)(a).

Figure \(\PageIndex{5}\). Subdividing the area into rectangles.

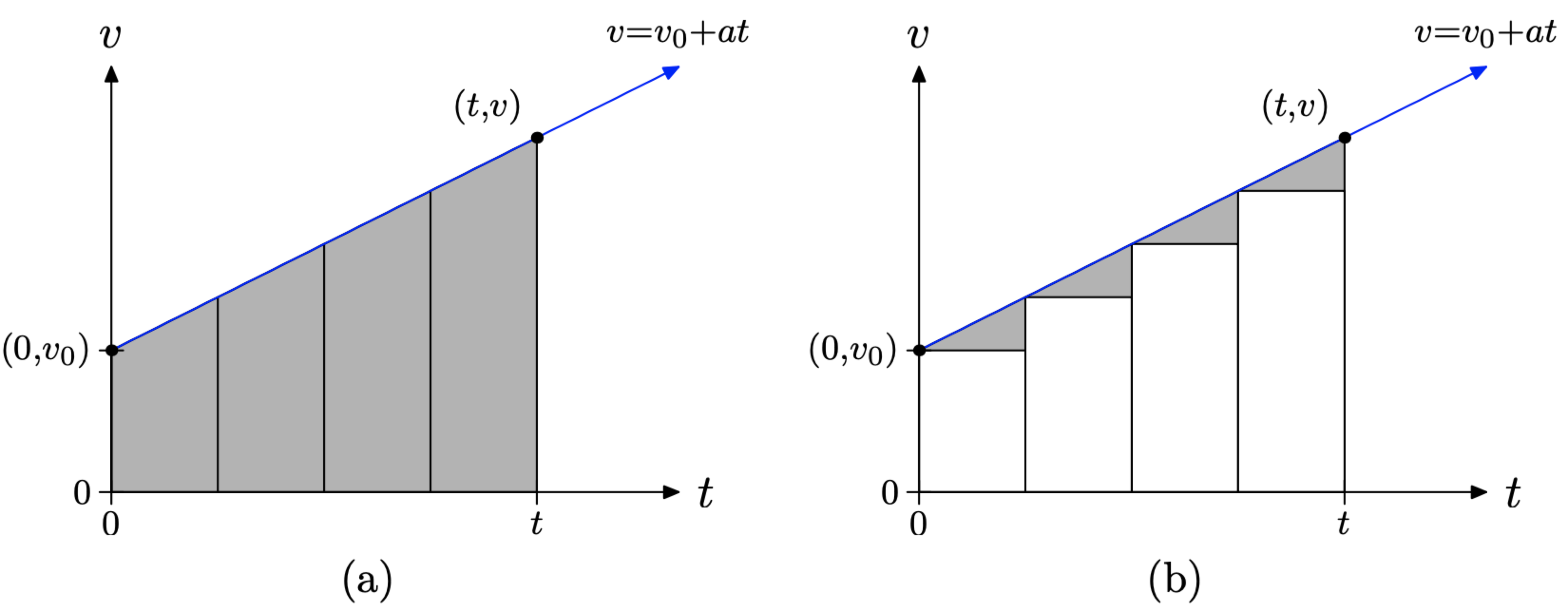
Next, use the left endpoint of each subinterval of time to draw four rectangles and fill them with the color white, as shown in Figure \(\PageIndex{5}\)(b). The top of each rectangle is horizontal, so we know that this represents uniform (constant) speed. Therefore, the area of each white rectangle represents the distance traveled during that subinterval of time. If we sum the areas of all four rectangles, then we get the total distance traveled during the time span [0, t], with, of course, the assumption that the speed is constant during each of the subintervals of time.

However, the speed is not constant during each subinterval of time, so the sum of the areas of the rectangles only approximates the total distance traveled on the time interval [0, t].

The key idea is to draw more rectangles. In Figure \(\PageIndex{6}\)(a), we’ve divided the time interval [0, t] into 8 equal subintervals of time. In Figure \(\PageIndex{6}\)(b), we again use the left endpoints of each subinterval of time to draw rectangles and we fill them with the color white.

Again, the top of each white rectangle is horizontal, which represents a uniform (constant) speed on that subinterval of time. Therefore, the area of each white rectangle again represents the distance traveled during that subinterval of time. The sum of all 8 rectangles represents the distance traveled during the time interval [0, t], assuming that the speed is constant during each of the subintervals of time.

However, the speed is not constant on the time interval [0, t], so the sum of the eight rectangles only offers an approximation of the distance traveled during the time interval [0, t], albeit a better approximation than that offered by the sum of the areas of only four rectangles in Figure \(\PageIndex{5}\)(b).

As we subdivide the time interval [0, t] further, two things will happen

Figure \(\PageIndex{6}\). Subdividing the area into rectangles.

1. The subintervals of time will become smaller (in fact, infinitesimally small). When that happens, it becomes more and more reasonable to assume that the speed is constant during that subinterval of time. Therefore, in the limit, the sum of the areas of the rectangles will represent the total distance traveled over the time interval [0, t].
2. The sum of the areas of the rectangles converges to the area of the shaded region under the speed curve in Figure \(\PageIndex{4}\)(a).

This argument leads to one compelling conclusion.

Area Equals Distance Traveled

The area under the speed curve \(v = v_{0} + at\) over the time interval [0, t] represents the distance traveled during the time interval [0, t].

In Figure \(\PageIndex{7}\), the shaded region under \(v = v_{0} + at\) is a trapezoid. To find the area of this trapezoid, we add the bases (parallel sides) together, multiply by the height, then take half of the result.

Figure \(\PageIndex{7}\). The area of the shaded trapezoidal region represents the distance traveled.

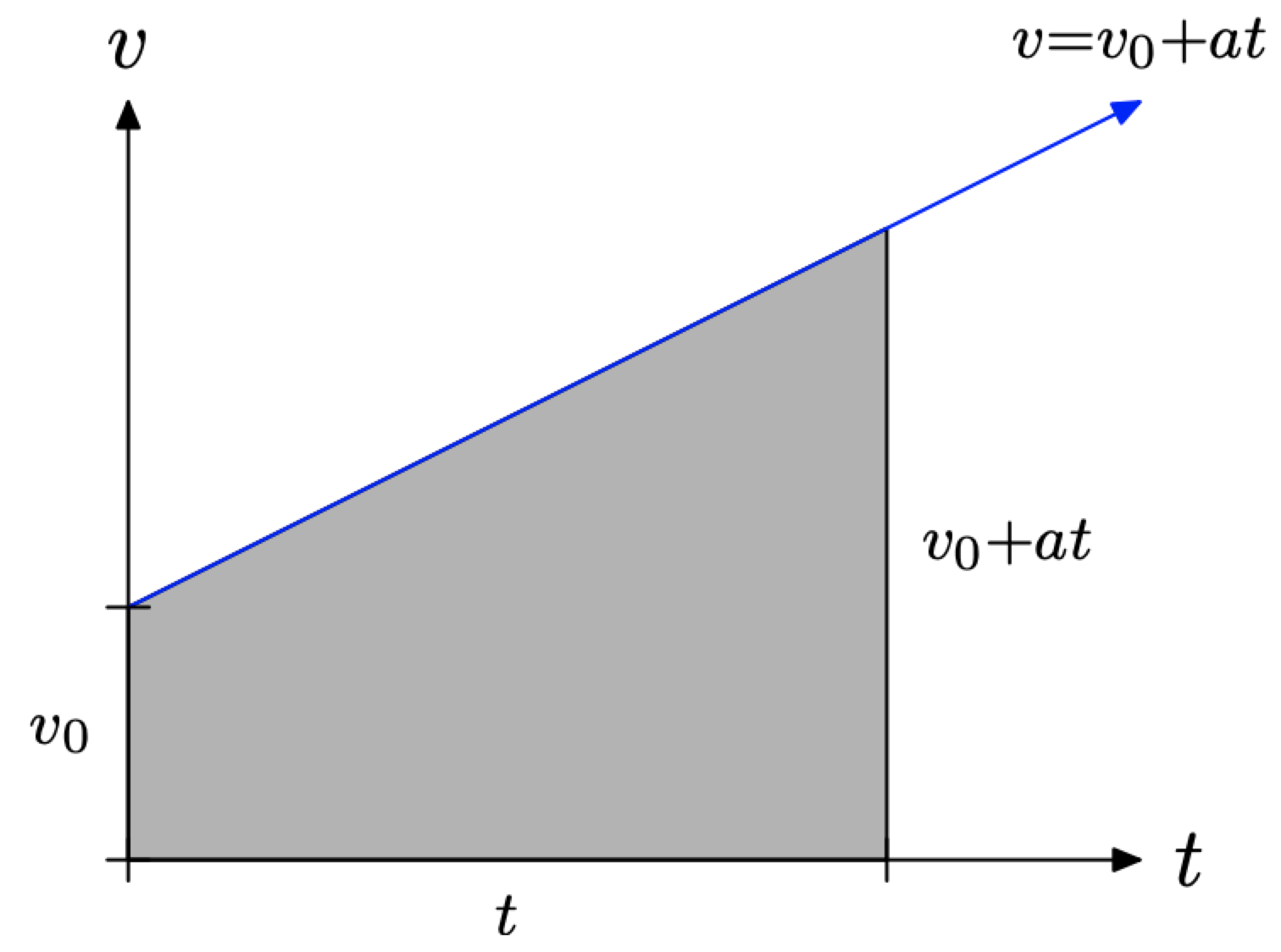
Thus, the area of the shaded region in Figure \(\PageIndex{7}\) is given by the formula

\[\text { Area }=\frac{1}{2}\left[v_{0}+\left(v_{0}+a t\right)\right] t \nonumber \]

Sum the quantity inside the parentheses, then distribute the 1/2 and the t to obtain

\[\text { Area }=v_{0} t+\frac{1}{2} a t^{2} \nonumber \]

Motion in One Dimension

Suppose that a particle is constrained to move along the real line. In addition, suppose that at time t = 0, the initial position of the particle is at \(x_{0}\) and the particle has initial speed \(v_{0}\) and is moving to the right (as shown in Figure \(\PageIndex{8}\)). Let’s assume that the particle experiences uniform acceleration a that is positive so that the particle continues to move to the right with increasing speed. At time t, let the particle’s position be denoted by x and its speed by v (also shown in Figure \(\PageIndex{8}\)).

Figure \(\PageIndex{8}\). A particle moves on the line with uniform acceleration.

Because we’ve assumed that the particle moves to the right with increasing speed, the distance traveled by the particle is given by the expression \(x − x_{0}\). However, we’ve also learned that the distance traveled is the area under the graph of the velocity (shown in Figure \(\PageIndex{7}\)), which we calculated in equation (7) to be \(v_{0} t+ (1/2)at^2\). We conclude that \[x-x_{0}=v_{0} t+\frac{1}{2} a t^{2} \nonumber \]

which leads to the second equation of motion.

Second Equation of Motion

Suppose that a particle moves on the real line with uniform acceleration a. Moreover, assume that the particle’s position and speed at time t = 0 are given by x0 and v0, respectively. Let x represent the particle’s position at time t. Then, the particle’s position at time t is given by the formula

\[x=x_{0}+v_{0} t+\frac{1}{2} a t^{2} \nonumber \]

In developing the equation of motion equation (9), we’ve avoided the notion of velocity. However, if a particle is constrained to move along the real line, it can move to the right or it can move to the left. This adds another dimension to speed.

Let’s draw a number line (as shown in Figure \(\PageIndex{9}\)), locate the origin, and agree that positive displacements are to the right and negative displacements are to the left.

Figure \(\PageIndex{9}\). Orienting the real line

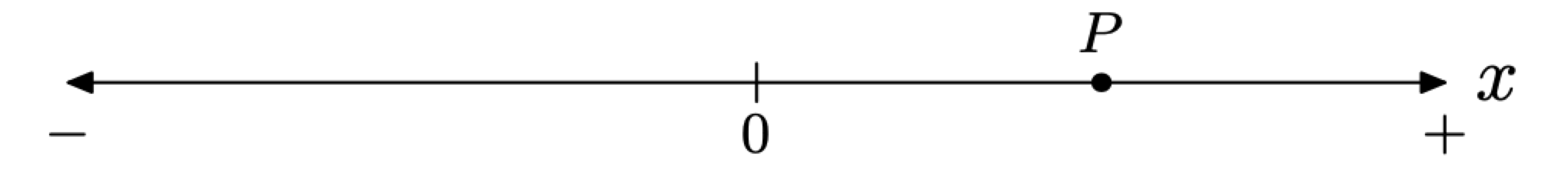
Next, we define what is meant by velocity

Definition

Velocity is the rate at which an object’s position is changing with respect to time.

For example, suppose that displacements on the oriented line in Figure \(\PageIndex{9}\) are measured in meters. Furthermore, suppose that the particle at point P in Figure \(\PageIndex{9}\) has velocity v = 20 meters per second. This would mean that the position of the particle is changing by a positive 20 meters each second. Because of the way we’ve oriented the line Figure \(\PageIndex{9}\), this means that the particle is moving to the right at a rate of 20 meters per second.

On the other hand, if the velocity of the particle at point P was v = −20 meters per second, this would mean that the position of the particle is changing by a negative 20 meters each second. Because of the orientation we’ve chosen in Figure \(\PageIndex{9}\), this would mean that the particle is moving to the left at a rate of 20 meters per second.

Note that in each case (positive or negative velocity) the speed is 20 meters per second. What velocity brings to the table is an additional attribute of orientation. The sign of the velocity indicates a direction, while the magnitude of the velocity indicates a speed.

It is important for us to state that the equations of motion apply equally well when we introduce the notion of velocity. Thus, we can summarize as follows.

The Equations of Motion

Suppose that a particle moves on an oriented real line with uniform acceleration a. Further, let \(x_{0}\) and \(v_{0}\) represent the initial position and velocity of the particle at time t = 0.

• The velocity v of the particle at time t is given by the formula \(v = v_{0} + at\).
• The position x of the particle at time t is given by the formula \(x = x_{0} + v_{0} t + \frac{1}{2} at^2\).

Let’s look at some applications of these Equations of Motion.

Example \(\PageIndex{4}\)

Orient the real line as in Figure \(\PageIndex{9}\). Suppose that at time t = 0 the particle is located 2 meters to the right of the origin and is moving at a rate of 3 meters per second. Further, suppose that particle is moving with a uniform acceleration of \(1.5 m/s^2\). Find the speed and position of the particle at the end of 10 seconds.

Solution

We’re given that \(v_{0} = 3\) m/s and \(a = 1.5 m/s^2\). Thus, after t = 10 seconds,

\[\begin{array}{l}{v=v_{0}+a t} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+1.5 \frac{\mathrm{m} / \mathrm{s}}{\not{s}} \times 10 \not{\mathrm{s}}} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+15 \frac{\mathrm{m}}{\mathrm{s}}} \\ {v=18 \frac{\mathrm{m}}{\mathrm{s}}}\end{array} \nonumber \]

We’re also given that \(x_{0} = 2\) m. Thus, after t = 10 seconds

\[\begin{aligned} x &=x_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\mathrm{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)(10 \mathrm{s})^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\not{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\not{\mathrm{s}^{2}}}\right)\left(100 \not{\mathrm{s}^{2}}\right) \\ x &=2 \mathrm{m}+30 \mathrm{m}+75 \mathrm{m} \\ x &=107 \mathrm{m} \end{aligned} \nonumber \]

Thus, at the end of t = 10 seconds, the particle is located 107 meters to the right of the origin and has velocity 18 meters per second (it is moving to the right with speed 18 meters per second)

Let’s look at another application of the Equations of Motion.

Example \(\PageIndex{5}\)

A car is traveling down the highway at a speed of 60 miles per hour. Suddenly, a deer appears in the road ahead and the driver applies the brakes, decelerating the car at a constant rate of 12.9 feet per second every second. How long does it take the car to stop and how far does it travel during this time

Solution

The velocity of the car is given by the formula v = v0 + at. The car will stop when v = 0. Therefore, substitute v = 0 in the formula and solve for t

\[\begin{array}{l}{v=v_{0}+a t} \\ {0=v_{0}+a t} \\ {t=-\frac{v_{0}}{a}}\end{array} \nonumber \]

At time t = 0, the car’s initial velocity is v0 = 60 mi/h. The car is decelerating so it is losing speed at the given rate of 12.9 feet per second every second; i.e., \(a = −12.9 ft/s^2\). We could try substituting these numbers into our last result

\[t=-\frac{60 \mathrm{mi} / \mathrm{h}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}} \nonumber \]

The problem is immediately apparent: the units will not cancel. We have two choices; we can either (1) change the initial velocity into feet per second, or (2) change the acceleration into miles per hour per hour. We will do the former with the following calculation.

\[v_{0} = \frac{60\not{\text{mi}}}{\not{\text{h}}} \times \frac{5280\text{ft}}{\not{\text{mi}}} \times \frac{1\not{\text{h}}}{60\not{\text{min}}} \times \frac{1\not{\text{min}}}{60\not{\text{s}}} = 88\text{ft/s} \nonumber \]

We’ll substitute this number in equation (13).

\[\begin{aligned} t &=-\frac{v_{0}}{a} \\ t &=-\frac{88 \mathrm{ft} / \mathrm{s}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx 6.8 \mathrm{s} \end{aligned} \nonumber \]

Again, it is important to check the units. Note that

\[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s} \nonumber \]

which is the correct unit for time.

We’ll now find the stopping distance by letting the initial position of the car be \(x_{0} = 0\) feet. Thus, \(x = x_{0} + v_{0} t + (1/2)at^2\) becomes

\[x=v_{0} t+\frac{1}{2} a t^{2} \nonumber \]

and x will represent the stopping distance.

Now, substitute the initial speed v0 = 88 feet per second, the acceleration a = −12.9 feet per second each second, and the stopping time t = 6.8 seconds. Thus,

\[\begin{aligned} x &=v_{0} t+\frac{1}{2} a t^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\mathrm{s}}\right)(6.8 \mathrm{s})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft} / \mathrm{s}}{\mathrm{s}}\right)(6.8 \mathrm{s})^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\not{s}}\right)(6.8 \not{\mathrm{s}})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft}}{\not{\mathrm{s}^{2}}}\right)\left(46.24 \not{\mathrm{s}^{2}}\right) \\ x &=598.4 \mathrm{ft}-298.248 \mathrm{ft} \\ x & \approx 300 \mathrm{ft} \end{aligned} \nonumber \]

where we’ve rounded the stopping distance to the nearest foot.

The Acceleration Due to Gravity

If we neglect air resistance, then a body will fall to the surface of the earth with uniform acceleration. Physicists use the letter g to represent the acceleration due to gravity. Near the surface of the earth, this acceleration is given by \(g=32 \mathrm{ft} / \mathrm{s}^{2}\) or, in the metric system, \(g=9.8 \mathrm{m} / \mathrm{s}^{2}\).

Remember, acceleration is the rate at which a body’s velocity is changing with respect to time. Consequently, if we drop a body from rest at a very large height, after 1 second, its velocity will be 32 feet per second. After 2 seconds, its speed will be 64 feet per second. After 3 seconds, its speed will be 96 feet per second. Note how the speed is changing at a rate of 32 feet per second every second of time.

Gravity always attracts an object to the center of the earth, so we have to keep this in mind when using the Equations of Motion.

Let’s look at an example.

Example \(\PageIndex{6}\)

A ball is released from rest from a hot-air balloon that is hovering at a distance of 2000 feet above the surface of the earth. How long will it take until the ball strikes the ground?

Solution

In this exercise, we’ll rotate the real line so that it is vertical, as shown in Figure \(\PageIndex{10}\)(a). We’ll set the origin at ground level and let the positive y-direction point upward (indicated by the + sign at the top of the line in Figure \(\PageIndex{10}\)(a).

Figure \(\PageIndex{10}\).

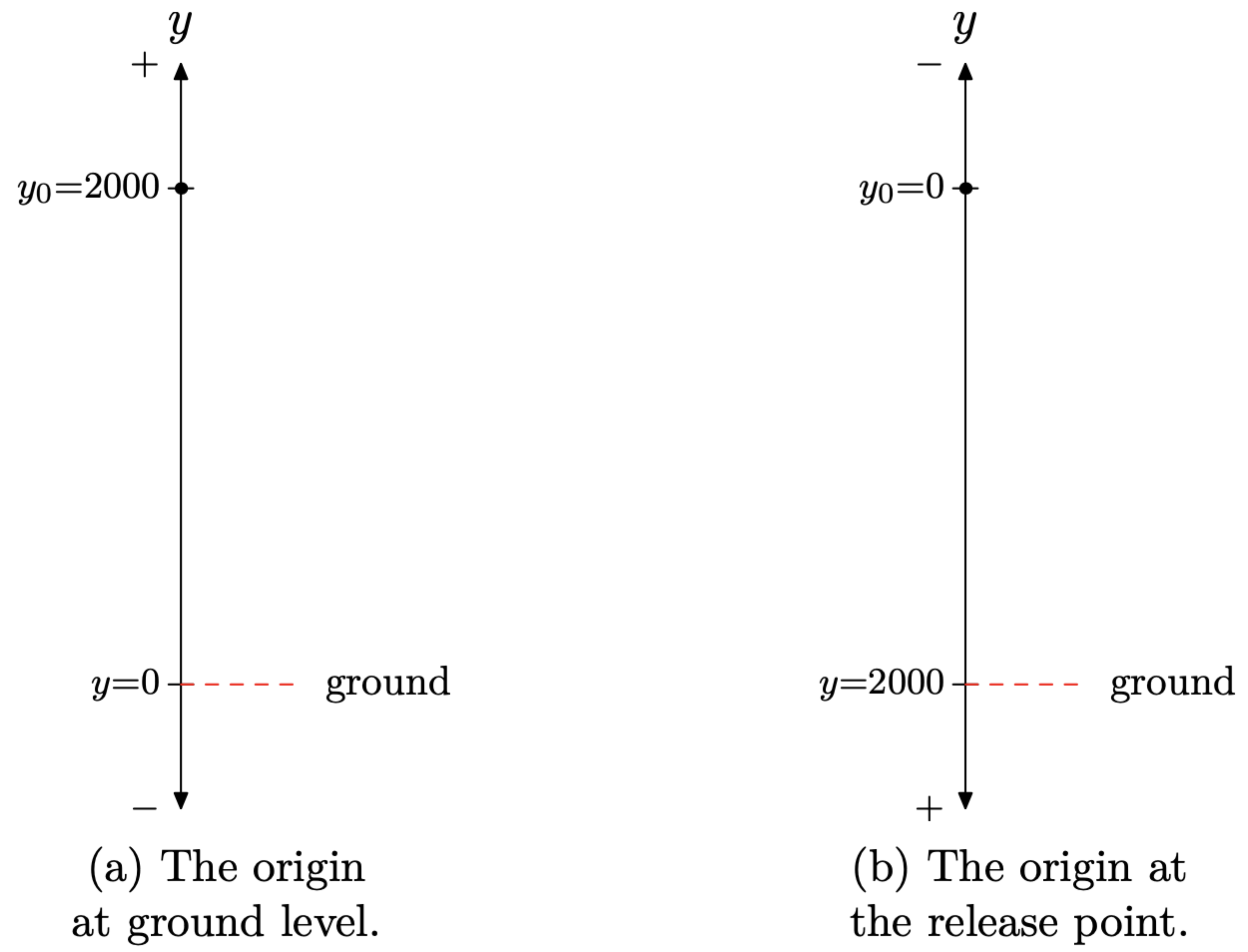
We’ll start with the equation \(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\), and then note that the initial velocity is \(v_{0} = 0\) feet per second (the ball is released from rest), so the equation becomes \[y=y_{0}+\frac{1}{2} a t^{2} \nonumber \]

We’re asked to find when the ball hits the ground, so that means we’re asked to find when y = 0 (see Figure \(\PageIndex{10}\)(a). Set y = 0 in the last equation and solve for t.

\[\begin{aligned} 0 &=y_{0}+\frac{1}{2} a t^{2} \\ t^{2} &=-\frac{2 y_{0}}{a} \\ t &=\sqrt{-\frac{2 y_{0}}{a}} \end{aligned} \nonumber \]

Note that positive displacements are upward (see Figure 10(a)). If the velocity is positive, the ball is moving upward. In our case, the ball is moving downward, so the velocity is negative. As the ball moves downward, its speed becomes greater, so the velocity becomes more and more negative. Hence, the acceleration must be negative; i.e., \(a = −32 ft/s^2\). Substitute this acceleration and the initial position y0 = 2000 ft into the last result and simplify

\[\begin{aligned} t &=\sqrt{-\frac{2(2000 \mathrm{ft})}{-32 \mathrm{ft} / \mathrm{s}^{2}}} \\ t & \approx 11.2 \mathrm{s} \end{aligned} \nonumber \]
We’ve rounded the result to the nearest tenth of a second. Again, checking the units is important. In this case,

\[\sqrt{\frac{\mathrm{ft}}{\mathrm{ft} / \mathrm{s}^{2}}}=\sqrt{\mathrm{ft} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}}=\sqrt{\mathrm{s}^{2}}=\mathrm{s} \nonumber \]

Alternatively, we could set up the real line as shown in Figure 10(b), where we’ve placed the origin at the point of release and reversed the orientation (the positive ydirection is now downward). Thus, the initial position is \(y_{0} = 0\) feet and the initial velocity is \(v_{0} = 0\) feet per second (the ball is released from rest). Set these values in the equation \(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) and solve for t.

\[\begin{aligned} y &=\frac{1}{2} a t^{2} \\ t^{2} &=\frac{2 y}{a} \\ t &=\sqrt{\frac{2 y}{a}} \end{aligned} \nonumber \]

Positive displacements are in the downward direction (note the reversal of orientation in Figure \(\PageIndex{10}\)(b)). This means that when the velocity is positive, the ball is moving downward. When we release the ball, it is going to pick up more speed, so the velocity becomes more and more positive. Hence, the acceleration is positive in this orientation; i.e., \(a = 32 ft/s^2\).

When the ball hits ground level, the position is y = 2000 ft. Substitute this value of y and the acceleration in the last result and simplify (check the units).

\[t=\sqrt{\frac{2(2000 \mathrm{ft})}{32 \mathrm{ft} / \mathrm{s}^{2}}} \nonumber \]

Note that this will give the same result as before; i.e., \(t \approx 11.2\) seconds.

Example \(\PageIndex{7}\)

A ball is thrown into the air from shoulder height (about 5 feet) with an initial upward velocity of 100 feet per second. Find the time it takes the ball to return to the ground.

Solution

Let’s find a solution using the graphing calculator. Using the orientation of Figure \(\PageIndex{10}\)(a), start with the equation

\[y=y_{0}+v_{0} t+\frac{1}{2} a t^{2} \nonumber \]

and note that the initial position is \(y_{0}=5\) feet, the initial velocity is \(v_{0} = 100\) feet per second, and the acceleration is a = −32 feet per second per second. Substitute these numbers into the previous equation to obtain

\[\begin{array}{l}{y=5+100 t+\frac{1}{2}(-32) t^{2}} \\ {y=5+100 t-16 t^{2}}\end{array} \nonumber \]

Enter this equation into the Y= menu as shown in Figure \(\PageIndex{11}\)(a). Adjust the window parameters as shown in Figure \(\PageIndex{11}\)(b) to produce the image shown in Figure \(\PageIndex{11}\)(c).

Figure \(\PageIndex{11}\) Using the graphing calculator to determine the time to return to the ground.

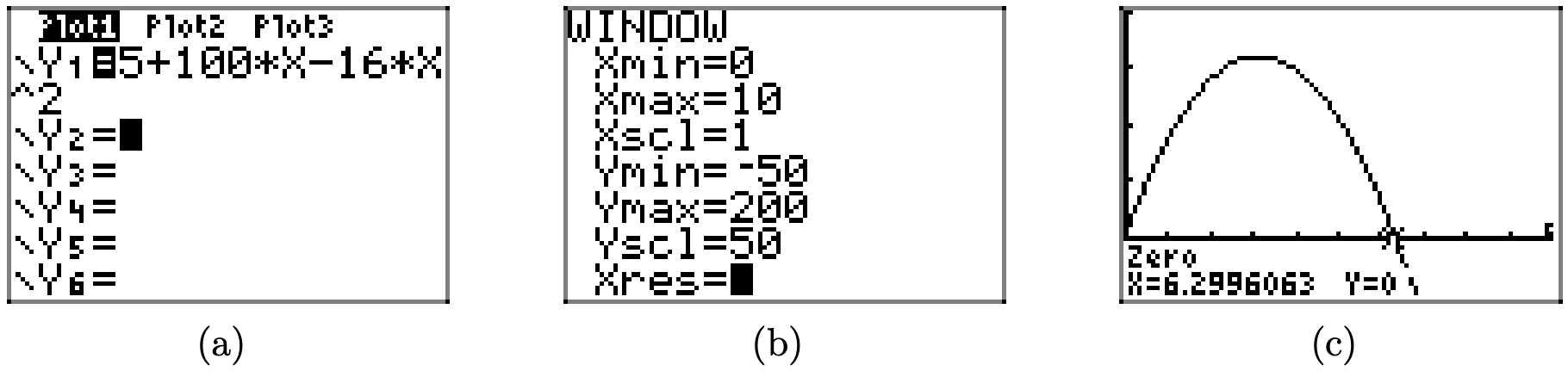
To determine the time it takes the ball to return to the ground, we must locate where the height of the ball is y = 0 feet. Because the graph in Figure \(\PageIndex{11}\)(c) is a plot of height or position (on the vertical axis) versus time (on the horizontal axis), this occurs when the graph in Figure \(\PageIndex{11}\)(c) crosses the horizontal axis; that is, at a zero of the function defined by \(y=5+100 t-16 t^{2}\). To determine this time, use the utility 2:zero in the CALC menu to determine the zero. The result is shown in Figure \(\PageIndex{11}\)(c), where we determine it takes approximately\(t \approx 6.29\) seconds for the ball to return to the ground.

Alternatively, we can set y = 0 in the equation \(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) and use the quadratic formula to solve for the time t.

\[\begin{aligned} 0 &=y_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-4\left(\frac{1}{2} a\right)\left(y_{0}\right)}}{2\left(\frac{1}{2} a\right)} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-2 a y_{0}}}{a} \end{aligned} \nonumber \]

We can now insert \(y_{0}=5 \mathrm{ft}, v_{0}=100 \mathrm{ft} / \mathrm{s},\) and \(a=-32 \mathrm{ft} / \mathrm{s}^{2}\), and then use a calculator to obtain

\[\begin{aligned} t &=\frac{-100 \mathrm{ft} / \mathrm{s} \pm \sqrt{(100 \mathrm{ft} / \mathrm{s})^{2}-2\left(-32 \mathrm{ft} / \mathrm{s}^{2}\right)(5 \mathrm{ft})}}{-32 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx-0.05,6.29 \mathrm{s} \end{aligned} \nonumber \]

The negative answer does not apply in this situation, so we keep the solution \(t \approx 6.29\) seconds. Note how this agrees with the solution found on the graphing calculator.

Again, it is important to make sure the units check. Underneath the radical, both terms have units \(\mathrm{ft}^{2} / \mathrm{s}^{2}\). When the square root is taken, these units become ft/s. Thus, both terms in the numerator are in ft/s, but the denominator has units \(\mathrm{ft} / \mathrm{s}^{2}\). When you invert and multiply, as we saw in Example \(\PageIndex{5}\), the units simplify to seconds.

Exercise

In Exercises 1-12, write down the formula d = vt and solve for the unknown quantity in the problem. Once that is completed, substitute the known quantities in the result and simplify. Make sure to check that your units cancel and provide the appropriate units for your solution.

Exercise \(\PageIndex{1}\)

If Martha maintains a constant speed of 30 miles per hour, how far will she travel in 5 hours?

Answer

150 miles

Exercise \(\PageIndex{2}\)

If Jamal maintains a constant speed of 25 miles per hour, how far will he travel in 5 hours?

Exercise \(\PageIndex{3}\)

If Arturo maintains a constant speed of 30 miles per hour, how long will it take him to travel 120 miles?

Answer

4 hours

Exercise \(\PageIndex{4}\)

If Mei maintains a constant speed of 25 miles per hour, how long will it take her to travel 150 miles?

Exercise \(\PageIndex{5}\)

If Allen maintains a constant speed and travels 250 miles in 5 hours, what is is his constant speed?

Answer

50 miles per hour

Exercise \(\PageIndex{6}\)

If Jane maintains a constant speed and travels 300 miles in 6 hours, what is is her constant speed?

Exercise \(\PageIndex{7}\)

If Jose maintains a constant speed of 15 feet per second, how far will he travel in 5 minutes?

Answer

4500 feet

Exercise \(\PageIndex{8}\)

If Tami maintains a constant speed of 1.5 feet per second, how far will she travel in 4 minutes?

Exercise \(\PageIndex{9}\)

If Carmen maintains a constant speed of 80 meters per minute, how far will she travel in 600 seconds?

Answer

800 meters

Exercise \(\PageIndex{10}\)

If Alphonso maintains a constant speed of 15 feet per second, how long will it take him to travel 1 mile? Note: 1 mile equals 5280 feet.

Exercise \(\PageIndex{11}\)

If Hoshi maintains a constant speed of 200 centimeters per second, how long will it take her to travel 20 meters? Note: 100 centimeters equals 1 meter.

Answer

10 seconds

Exercise \(\PageIndex{12}\)

If Maeko maintains a constant speed and travels 5 miles in 12 minutes, what is her speed in miles per hour?

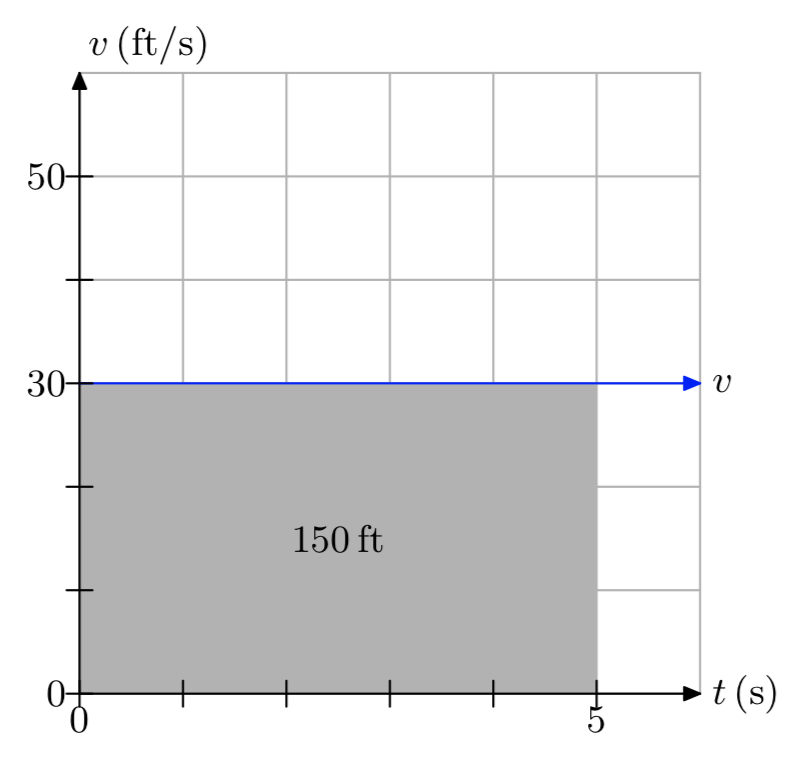
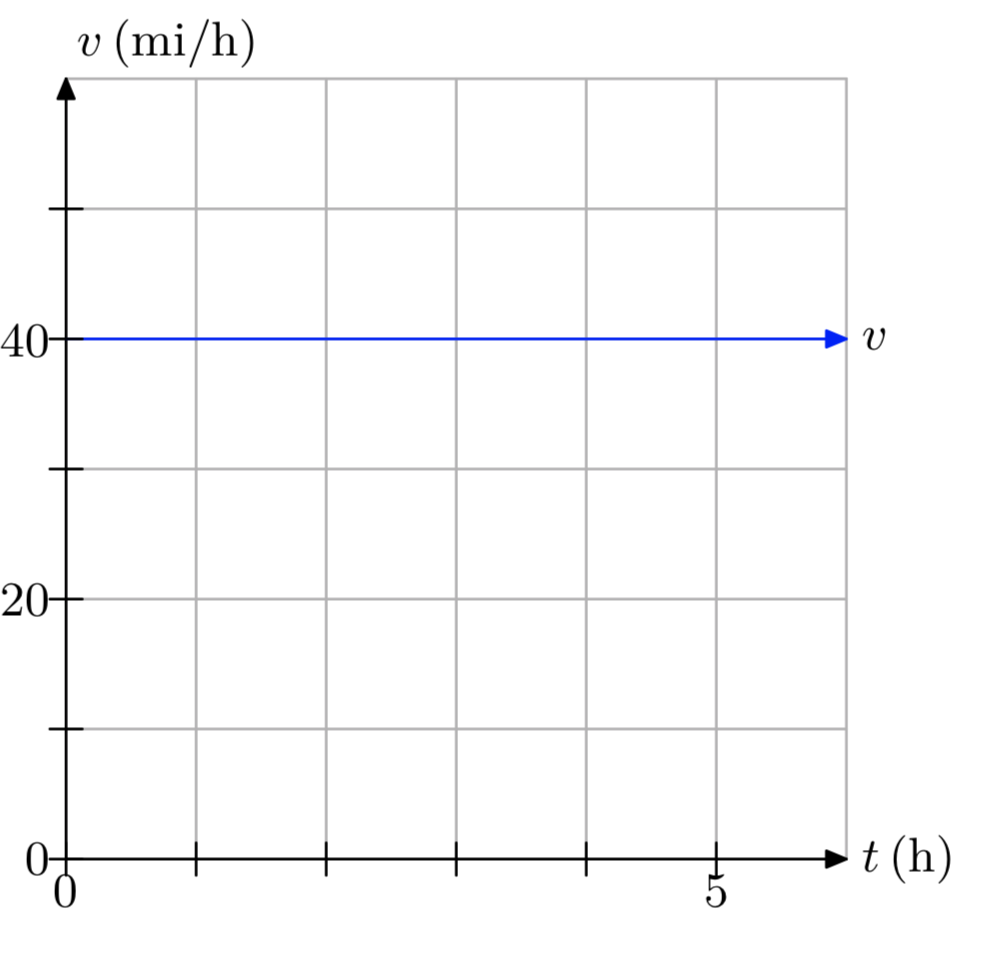
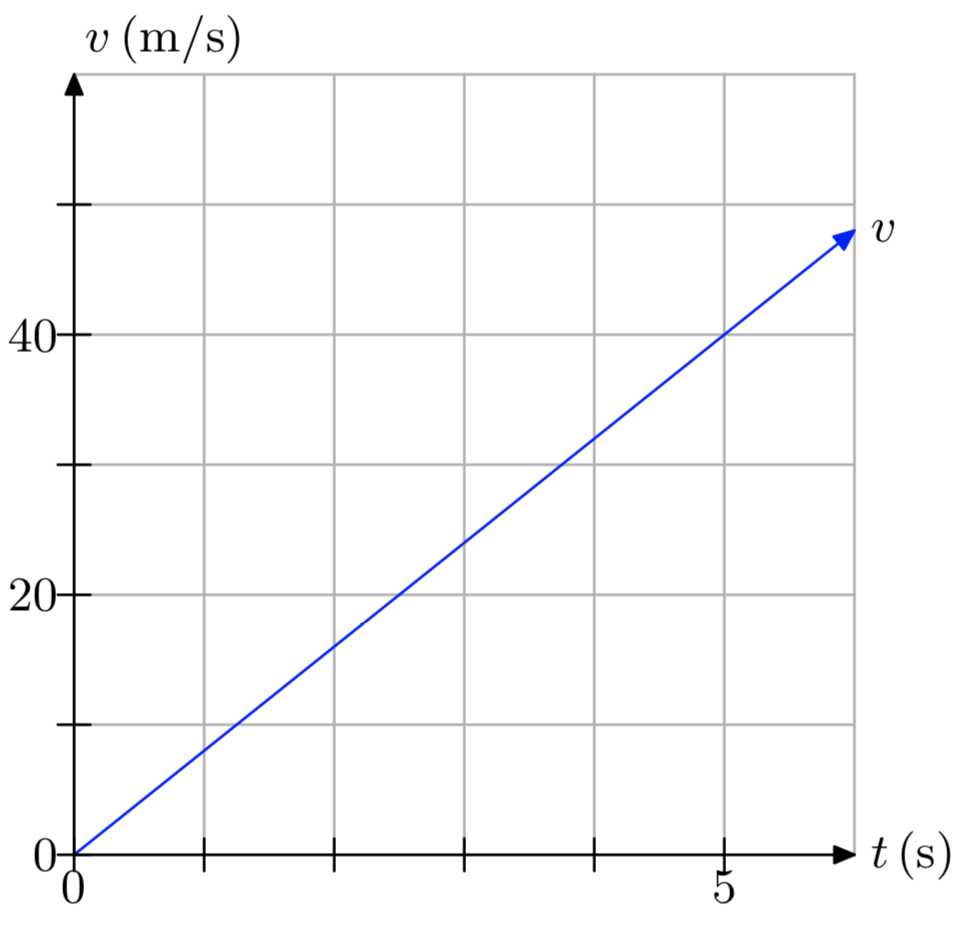
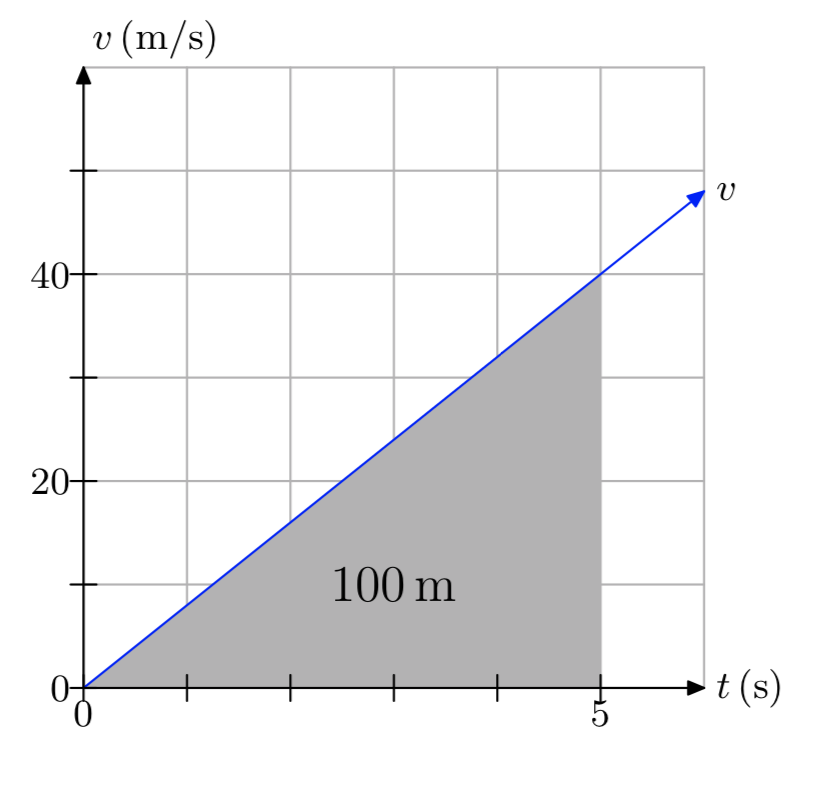
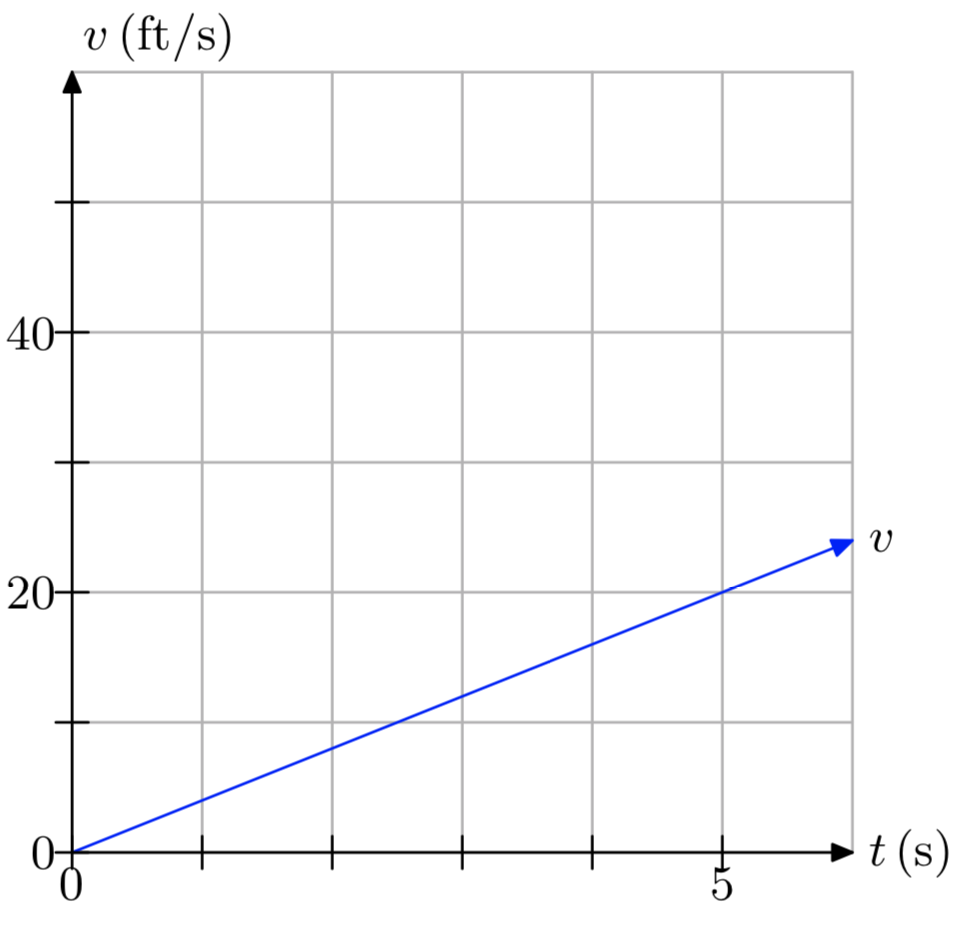
In Exercises 13-18, a plot of speed v versus time t is presented.

1. Make an accurate duplication of the plot on graph paper. Label and scale each axis. Mark the units on each axis.
2. Use the graph to determine the distance traveled over the time period [0,5], using the time units given on the graph.

Exercise \(\PageIndex{13}\)

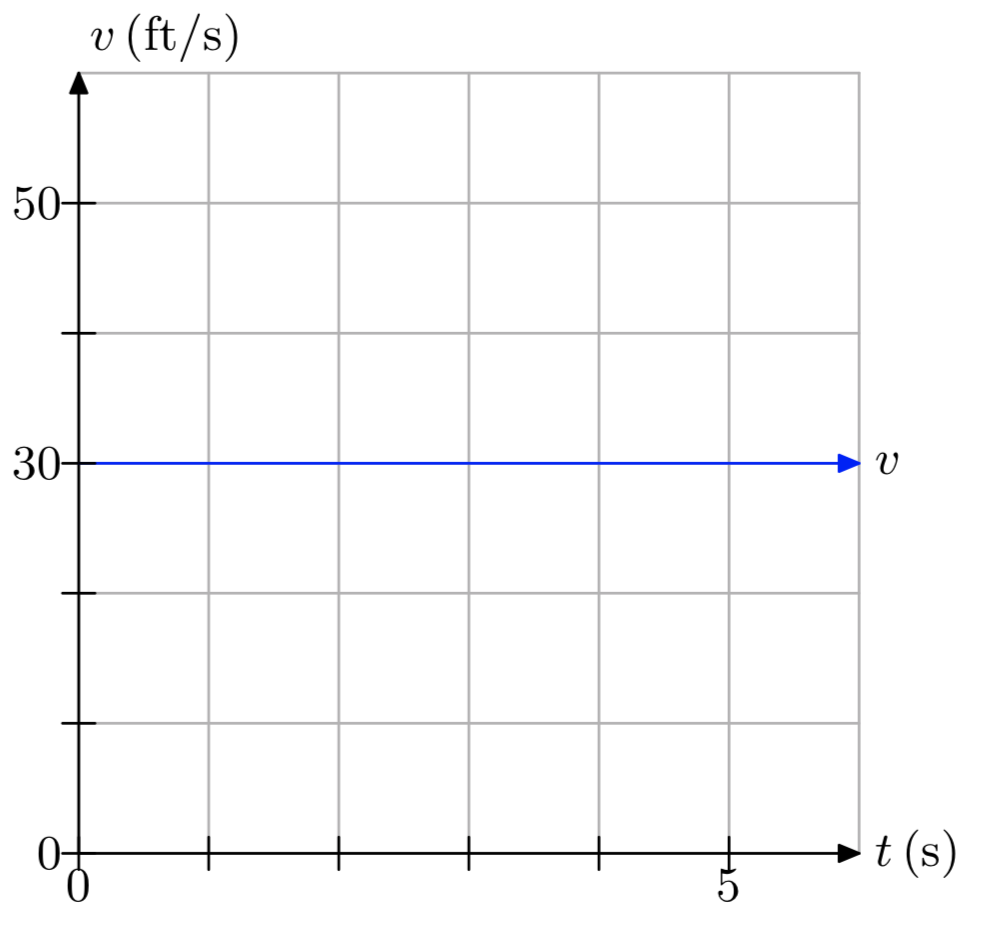
Answer

The distance traveled is 150 feet.

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Answer

The distance traveled is 100 meters.

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

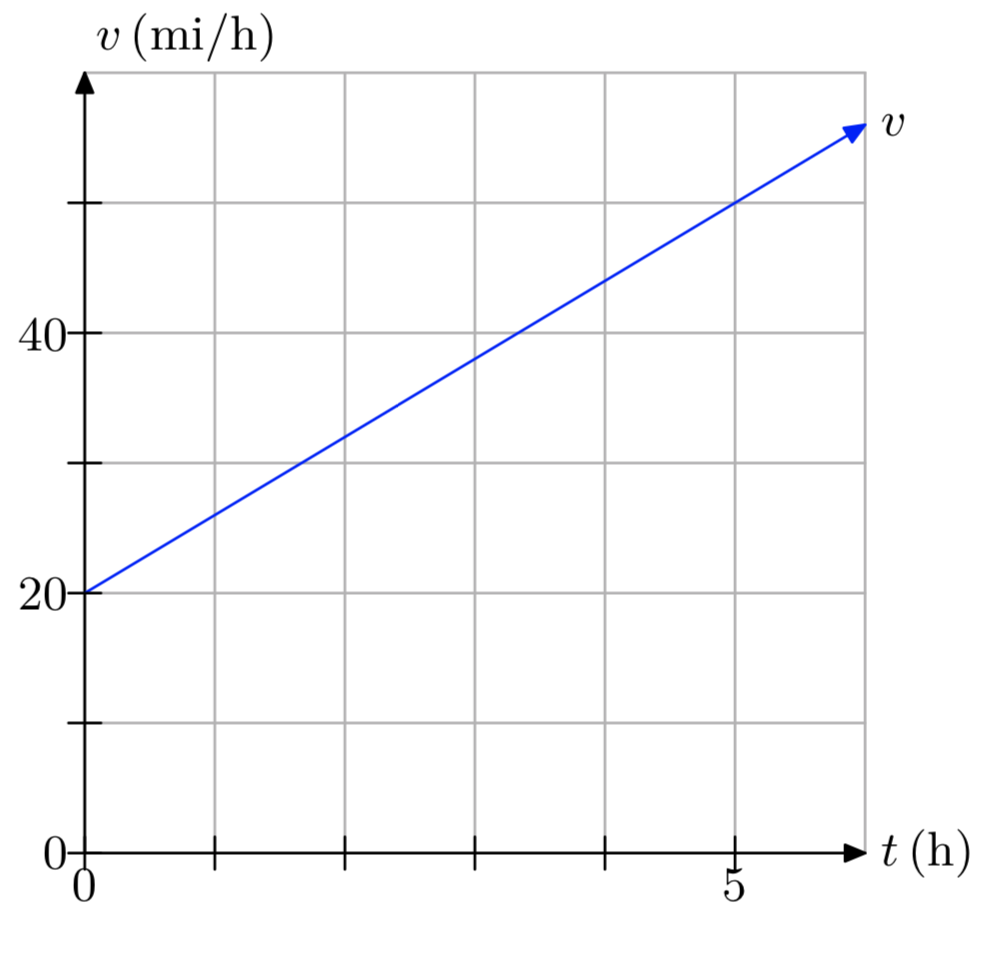
Answer

The distance traveled is 175 miles.

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

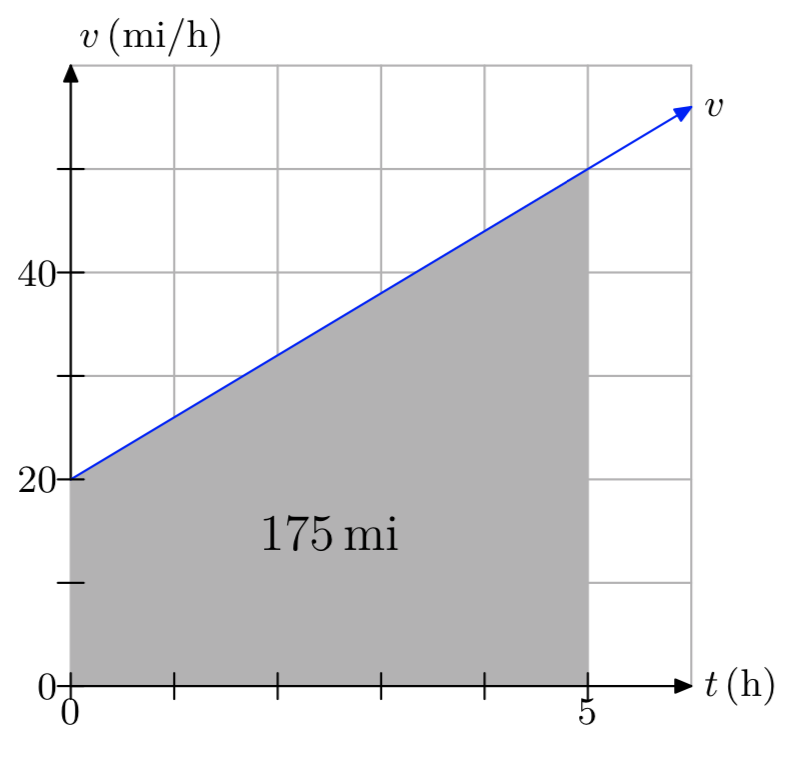
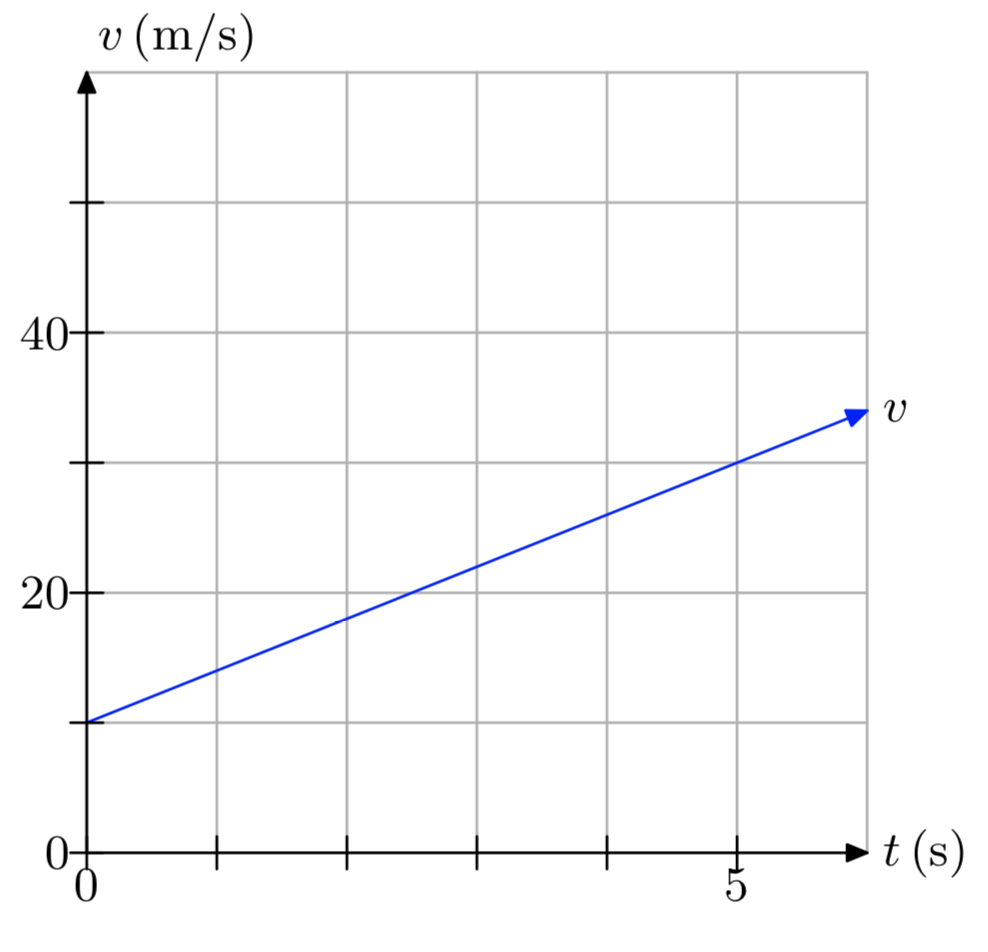
You’re told that a car moves with a constant acceleration of 7.5 ft/\(s^2\). In your own words, explain what this means.

Answer

It means that the velocity of the car increases at a rate of 7.5 feet per second every second.

Exercise \(\PageIndex{20}\)

You’re told that an object will fall on a distant planet with constant acceleration 6.5 m/\(s^2\). In your own words, explain what this means.

Exercise \(\PageIndex{21}\)

You’re told that the acceleration of a car is −18 ft/\(s^2\). In your own words, explain what this means.

Answer

It means that the velocity of the car is decreasing at a rate of 18 feet per second every second.

Exercise \(\PageIndex{22}\)

An observer on a distant planet throws an object into the air and as it moves upward he reports that the object has a constant acceleration of −4.5 m/\(s^2\). In your own words, explain what this means.

In Exercises 23-28, perform each of the following tasks.

1. Solve the equation \(v = v_{0} + at\) for the unknown quantity.
2. Substitute the known quantities (with units) into your result, then simplify. Make sure the units cancel and provide appropriate units for your solution.

Exercise \(\PageIndex{23}\)

A rocket accelerates from rest with constant acceleration 15.8 m/\(s^2\). What will be the speed of the rocket after 3 minutes?

Answer

2,844 m/s

Exercise \(\PageIndex{24}\)

A stone is dropped from rest on a distant planet and it accelerates towards the ground with constant acceleration 3.8ft/\(s^2\). What will be the speed of the stone after 2 minutes?

Exercise \(\PageIndex{25}\)

A stone is thrown downward on a distant planet with an initial speed of 20 ft/s. If the stone experiences constant acceleration of 32ft/\(s^2\), what will be the speed of the stone after 1 minute?

Answer

1,940 ft/s

Exercise \(\PageIndex{26}\)

A ball is hurled upward with an initial speed of 80m/s. If the ball experiences a constant acceleration of −9.8 m/\(s^2\), what will be the speed of the ball at the end of 5 seconds?

Exercise \(\PageIndex{27}\)

An object is shot into the air with an initial speed of 100m/s. If the object experiences constant deceleration of 9.8 m/\(s^2\), how long will it take the ball to reach its maximum height?

Answer

Approximately 10.2 seconds.

Exercise \(\PageIndex{28}\)

An object is released from rest on a distant planet and after 5 seconds, its speed is 98m/s. If the object falls with constant acceleration, determine the acceleration of the object.

In Exercises 29-42, use the appropriate equation of motion, either \(v = v_{0} + at\) or \(x = x_{0}+v_{0}t+\frac{1}{2}at^2\) or both, to solve the question posed in the exercise.

1. Select the appropriate equation of motion and solve for the unknown quantity.
2. Substitute the known quantities (with their units) into your result and simplify. Check that cancellation of units provide units appropriate for your solution.
3. Find a decimal approximation for your answer.

Exercise \(\PageIndex{29}\)

A rocket with initial velocity 30 m/s moves along a straight line with constant acceleration 2.5 m/\(s^2\). Find the velocity and the distance traveled by the rocket at the end of 10 seconds.

Answer

Velocity = 55 m/s, Distance traveled = 425 m.

Exercise \(\PageIndex{30}\)

A car is traveling at 88 ft/s when it applies the brakes and begins to slow with constant deceleration of 5 ft/\(s^2\). What is its speed and how far has it traveled at the end of 5 seconds?

Exercise \(\PageIndex{31}\)

A car is traveling at 88 ft/s when it applies the brakes and slows to 58 ft/s in 10 seconds. Assuming constant deceleration, find the deceleration and the distance traveled by the car in the 10 second time interval. Hint: Compute the deceleration first.

Answer

Acceleration = −3 ft/\(s^2\), Distance traveled = 730 ft.

Exercise \(\PageIndex{32}\)

A stone is hurled downward from above the surface of a distant planet with initial speed 45 m/s. At then end of 10 seconds, the velocity of the stone is 145 m/s. Assuming constant acceleration, find the acceleration of the stone and the distance traveled in the 10 second time period.

Exercise \(\PageIndex{33}\)

An object is shot into the air from the surface of the earth with an initial velocity of 180 ft/s. Find the maximum height of the object and the time it takes the object to reach that maximum height.Hint: The acceleration due to gravity near the surface of the earth is well known.

Answer

Time to max height = 5.625 s, Max height = 506.25 ft.

Exercise \(\PageIndex{34}\)

An object is shot into the air from the surface of a distant planet with an initial velocity of 180 m/s. Find the maximum height of the object and the time it takes the object to reach that maximum height. Assume that the acceleration due to gravity on this distant planet is 5.8 m/\(s^2\). Hint: Calculate the time to the maximum height first.

Exercise \(\PageIndex{35}\)

A car is traveling down the high- way at 55 mi/h when the driver spots a slide of rocks covering the road ahead and hits the brakes, providing a constant deceleration of 12 ft/\(s^2\). How long does it take the car to come to a halt and how far does it travel during this time period?

Answer

Time to stop \(\approx\) 6.72 s, Distance traveled \(\approx\) 271 ft

Exercise \(\PageIndex{36}\)

A car is traveling down the highway in Germany at 81 km/h when the driver spots that traffic is stopped in the road ahead and hits the brakes, providing a constant deceleration of 2.3 m/\(s^2\). How long does it take the car to come to a halt and how far does it travel during this time period? Note: 1 kilometer equals 1000 meters.

Exercise \(\PageIndex{37}\)

An object is released from rest at some distance over the surface of the earth. How far (in meters) will the object fall in 5 seconds and what will be its velocity at the end of this 5 second time period? Hint: You should know the acceleration due to gravity near the surface of the earth.

Answer

Distance = 122.5 m, Velocity = −49 m/s.

Exercise \(\PageIndex{38}\)

An object is released from rest at some distance over the surface of a distant planet. How far (in meters) will the object fall in 5 seconds and what will be its velocity at the end of this 5 second time period? Assume the acceleration due to gravity on the distant planet is 13.5 m/\(s^2\).

Exercise \(\PageIndex{39}\)

An object is released from rest at a distance of 352 feet over the surface of the earth. How long will it take the object to impact the ground?

Answer

Time \(\approx\) 4.69 s

Exercise \(\PageIndex{40}\)

An object is released from rest at a distance of 400 meters over the surface of a distant planet. How long will it take the object to impact the ground? Assume that the acceleration due to gravity on the distant planet equals 5.3 m/ (s^2\).

Exercise \(\PageIndex{41}\)

On earth, a ball is thrown upward from an initial height of 5 meters with an initial velocity of 100 m/s. How long will it take the ball to return to the ground?

Answer

Time \(\approx\) 20.5 s

Exercise \(\PageIndex{42}\)

On earth, a ball is thrown upward from an initial height of 5 feet with an initial velocity of 100 ft/s. How long will it take the ball to return to the ground?

A ball is thrown into the air near the surface of the earth. In Exercises 43-46, the initial height of the ball and the initial velocity of the ball are given. Complete the following tasks.

1. Use \(y = y_{0} +v_{0}t+\frac{1}{2}at^2\) to set up a formula for the height y of the ball as a function of time t. Use the appropriate constant for the acceleration due to gravity near the surface of the earth.
2. Load the equation from the previous part into Y1 in your graphing calculator. Adjust your viewing window so that both the vertex and the time when the ball returns to the ground are visible. Copy the image onto your homework paper. Label and scale each axis with xmin, xmax, ymin, and ymax.
3. Use the zero utility in the CALC menu of your graphing calculator to determine the time when the ball returns to the ground. Record this answer in the appropriate location on your graph.
4. Use the quadratic formula to determine the time the ball returns to the ground. Use your calculator to find a decimal approximation of your solution. It should agree with that found using the zero utility on your graphing calculator. Be stubborn! Check your work until the answers agree.

Exercise \(\PageIndex{43}\)

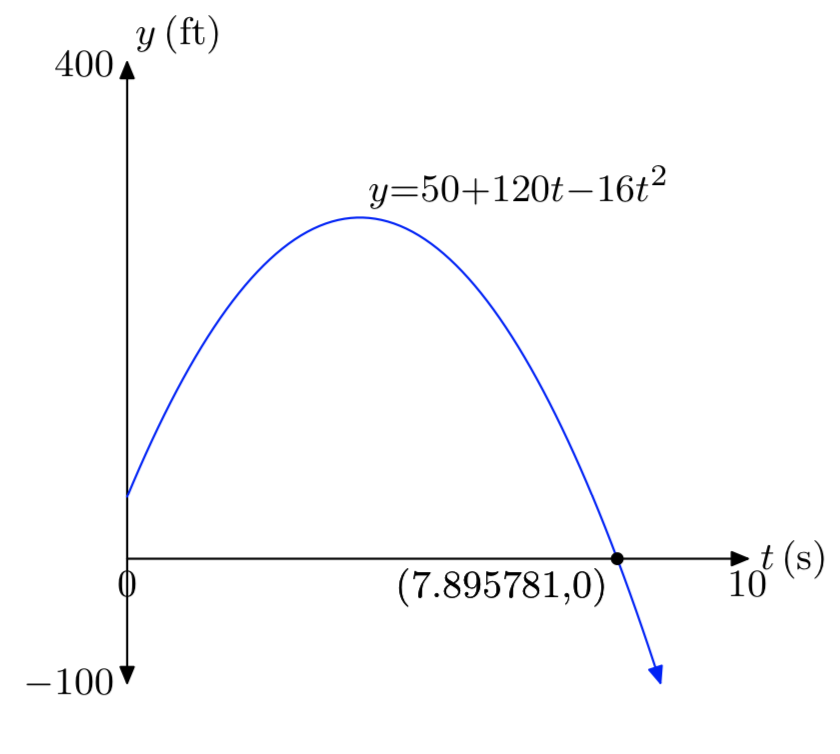
\(y_{0}\) = 50 ft, \(v_{0}\) = 120 ft/s.

Answer

Exercise \(\PageIndex{44}\)

\(y_{0}\) = 30 m, \(v_{0}\) = 100 m/s.

Exercise \(\PageIndex{45}\)

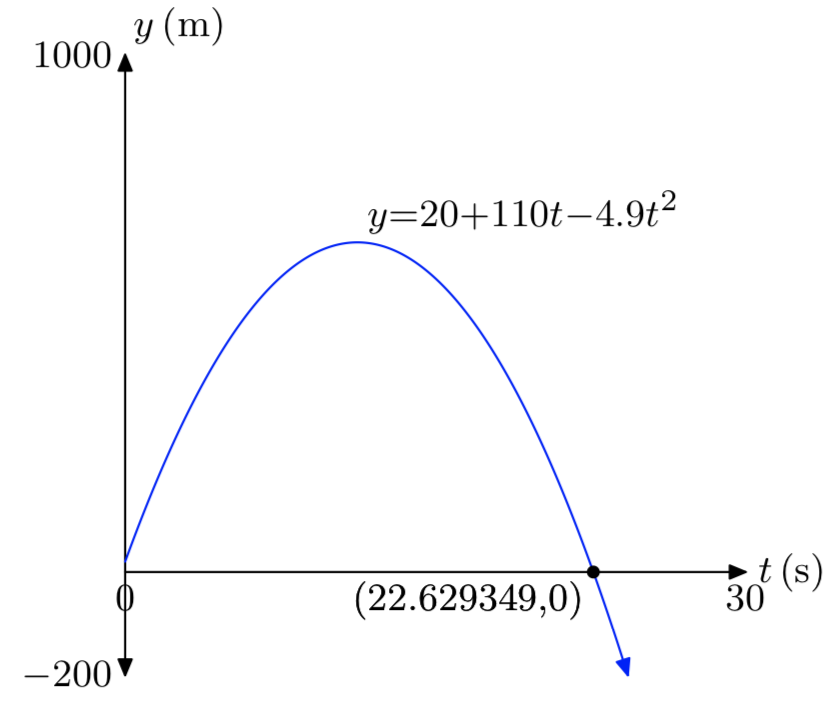
\(y_{0}\) = 20m, \(v_{0}\) = 110m/s.

Answer

Exercise \(\PageIndex{46}\)

\(y_{0}\) = 100ft, \(v_{0}\) = 200ft/s.

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{47}\)

A rock is thrown upward at an initial speed of 64 ft/s. How many seconds will it take the rock to rise 61 feet? Round your answer to the nearest hundredth of a second.

Answer

1.57 seconds

Exercise \(\PageIndex{48}\)

A penny is thrown downward from the top of a tree at an initial speed of 28 ft/s. How many seconds will it take the penny to fall 289 feet? Round your answer to the nearest hundredth of a second.

Exercise \(\PageIndex{49}\)

A water balloon is thrown downward from the roof of a building at an initial speed of 24 ft/s. The building is 169 feet tall. How many seconds will it take the water balloon to hit the ground? Round your answer to the nearest hundredth of a second.

Answer

2.59 seconds

Exercise \(\PageIndex{50}\)

A rock is thrown upward at an initial speed of 60 ft/s. How many seconds will it take the rock to rise 51 feet? Round your answer to the nearest hundredth of a second.

Exercise \(\PageIndex{51}\)

A ball is thrown upward from a height of 42 feet at an initial speed of 63 ft/s. How many seconds will it take the ball to hit the ground? Round your answer to the nearest hundredth of a second.

Answer

4.52 seconds

Exercise \(\PageIndex{52}\)

A rock is thrown upward from a height of 32 feet at an initial speed of 25 ft/s. How many seconds will it take the rock to hit the ground? Round your answer to the nearest hundredth of a second.

Exercise \(\PageIndex{53}\)

A penny is thrown downward from the top of a tree at an initial speed of 16 ft/s. The tree is 68 feet tall. How many seconds will it take the penny to hit the ground? Round your answer to the nearest hundredth of a second.

Answer

1.62 seconds

Exercise \(\PageIndex{54}\)

A penny is thrown downward off of the edge of a cliff at an initial speed of 32 ft/s. How many seconds will it take the penny to fall 210 feet? Round your answer to the nearest hundredth of a second.