5.6: Optimization

In this section we will explore the science of optimization. Suppose that you are trying to find a pair of numbers with a fixed sum so that the product of the two numbers is a maximum. This is an example of an optimization problem. However, optimization is not limited to finding a maximum. For example, consider the manufacturer who would like to minimize his costs based on certain criteria. This is another example of an optimization problem. As you can see, optimization can encompass finding either a maximum or a minimum.

Optimization can be applied to a broad family of different functions. However, in this section, we will concentrate on finding the maximums and minimums of quadratic functions. There is a large body of real-life applications that can be modeled by quadratic functions, so we will find that this is an excellent entry point into the study of optimization.

Finding the Maximum or Minimum of a Quadratic Function

Consider the quadratic function

\[f(x)=-x^{2}+4 x+2 \nonumber \]

Let’s complete the square to place this quadratic function in vertex form. First, factor out a minus sign.

\[f(x)=-\left[x^{2}-4 x-2\right] \nonumber \]

Take half of the coefficient of \(x\) and square, as in \([(1 / 2)(-4)]^{2}=4\). Add and subtract this amount to keep the equation balanced.

\[f(x)=-\left[x^{2}-4 x+4-4-2\right] \nonumber \]

Factor the perfect square trinomial, combine the constants at the end, and then redistribute the minus sign to place the quadratic function in vertex form.

\[\begin{array}{l}{f(x)=-\left[(x-2)^{2}-6\right]} \\ {f(x)=-(x-2)^{2}+6}\end{array} \nonumber \]

This is a parabola that opens downward, has been shifted 2 units to the right and 6 units upward. This places the vertex of the parabola at (2, 6), as shown in Figure 1. Note that the maximum function value (y-value) occurs at the vertex of the parabola. A mathematician would say that the function “attains a maximum value of 6 at \(x\) equals 2.”

Note that 6 is greater than or equal to any other y-value (function value) that occurs on the parabola. This gives rise to the following definition.

Figure \(\PageIndex{1}\). The maximum value of the function, 6, occurs at the vertex of the parabola, (2, 6).

Definition: Maximum

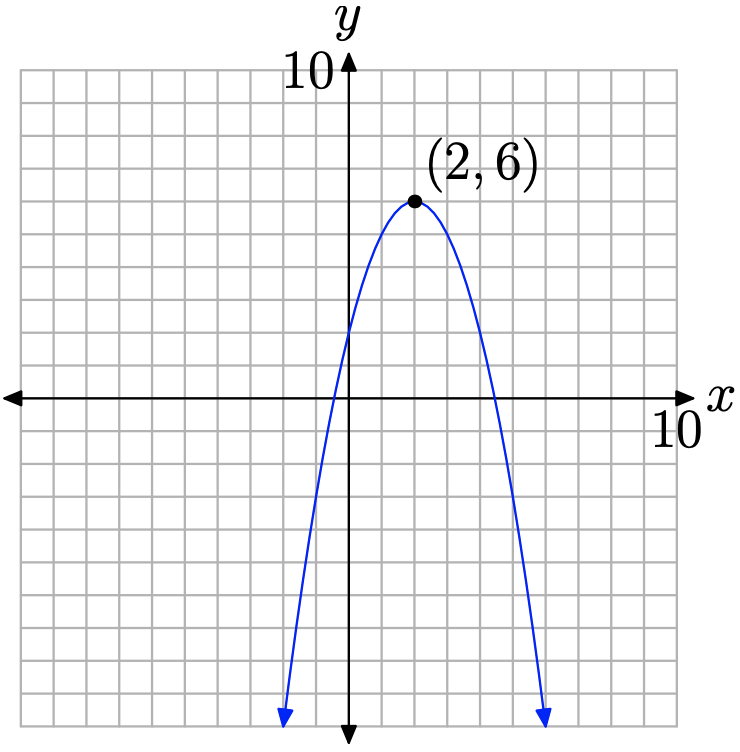
Let \(c\) be in the domain of \(f\). The function \(f\) is said to achieve a maximum at \(x=c\) if \(f(c) \geq f(x)\) for all \(x\) in the domain of \(f\).

Next, let’s look at a quadratic function that attains a minimum on its domain.

Example \(\PageIndex{1}\)

Next, let’s look at a quadratic function that attains a minimum on its domain.

\[f(x)=2 x^{2}+12 x+12 \nonumber \]

Solution

Factor out a 2. \[f(x)=2\left[x^{2}+6 x+6\right] \nonumber \]

Take half of the coefficient of x and square, as in \([(1 / 2)(6)]^{2}=9\). Add and subtract this amount to keep the equation balanced.

\[f(x)=2\left[x^{2}+6 x+9-9+6\right] \nonumber \]

Factor the trinomial and combine the constants, and then redistribute the 2 in the next step.

\[\begin{array}{l}{f(x)=2\left[(x+3)^{2}-3\right]} \\ {f(x)=2(x+3)^{2}-6}\end{array} \nonumber \]

The graph is a parabola that opens upward, shifted 3 units to the left and 6 units downward. This places the vertex at (−3, −6), as shown in Figure \(\PageIndex{2}\). Note that the minimum function value (y-value) occurs at the vertex of the parabola. A mathematician would say that the function “attains a minimum value of −6 at x equals −3.

Figure \(\PageIndex{2}\). The minimum value of the function, -6, occurs at the vertex of the parabola, (−3, −6).

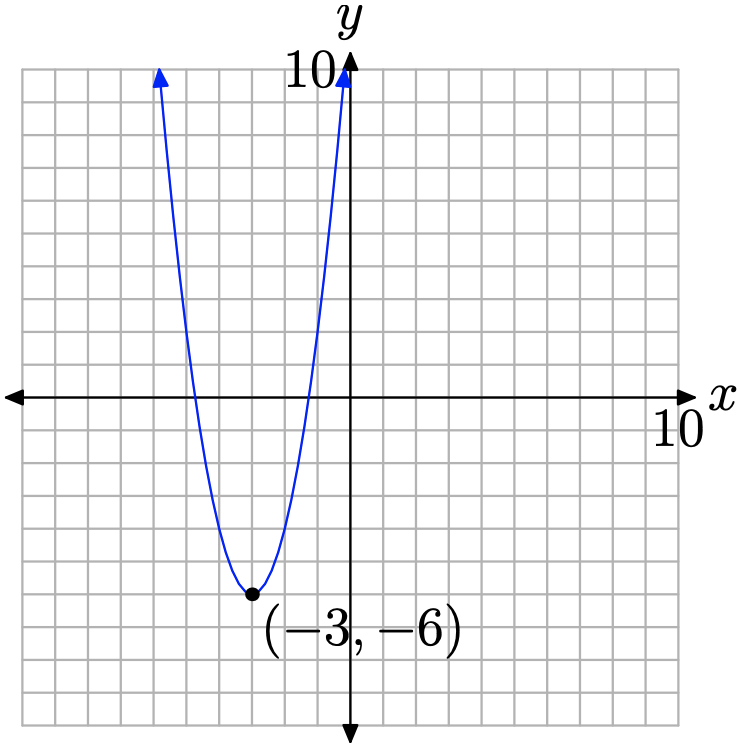
Note that −6 is less than or equal to any other y-value (function value) that occurs on the parabola.

This last example gives rise to the following definition.

Definition

Let c be in the domain of f. The function f is said to achieve a minimum at x = c if \(f(c) \leq f(x)\) for all x in the domain of f.

A Shortcut for the Vertex

It should now be clear that the vertex of the parabola plays a crucial role when optimizing a quadratic function. We also know that we can complete the square to find the coordinates of the vertex. However, it would be nice if we had a quicker way of finding the coordinates of the vertex. Let’s look at the general quadratic function

\[y=a x^{2}+b x+c \nonumber \]

and complete the square to find the coordinates of the vertex. First, factor out the a.

\[y=a\left[x^{2}+\frac{b}{a} x+\frac{c}{a}\right] \nonumber \]

Take half of the coefficient of x and square, as in \([(1 / 2)(b / a)]^{2}=[b /(2 a)]^{2}=b^{2} /\left(4 a^{2}\right)\). Add and subtract this amount to keep the equation balanced.

\[y=a\left[x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}-\frac{b^{2}}{4 a^{2}}+\frac{c}{a}\right] \nonumber \]

Factor the perfect square trinomial and make equivalent fractions for the constant terms with a common denominator.

\[\begin{array}{l}{y=a\left[\left(x+\frac{b}{2 a}\right)^{2}-\frac{b^{2}}{4 a^{2}}+\frac{4 a c}{4 a^{2}}\right]} \\ {y=a\left[\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\right]}\end{array} \nonumber \]

Finally, redistribute that a. Note how multiplying by a cancels one a in the denominator of the constant term.

\[y=a\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a} \nonumber \]

Now, here’s the key idea. The results depend upon the values of a, b, and c, but it should be clear that the coordinates of the vertex are

\[\left(-\frac{b}{2 a}, \frac{4 a c-b^{2}}{4 a}\right) \nonumber \]

The y-value of the vertex is a bit hard to memorize, but the x-value of the vertex is easy to memorize.

Vertex Shortcut

Given the parabola represented by the quadratic function \[y=a x^{2}+b x+c \nonumber \]

the x-coordinate of the vertex is given by the formula \[x_{\text { vertex }}=-\frac{b}{2 a} \nonumber \]

Let’s test this with the quadratic function given in Example \(\PageIndex{1}\).

Example \(\PageIndex{2}\)

Use the formula \(x_{\text { vertex }}=-b /(2 a)\) to find the x-coordinate of the vertex of the parabola represented by the quadratic function in Example \(\PageIndex{1}\).

Solution

In Example \(\PageIndex{1}\), the quadratic function was represented by the equation \[f(x)=2 x^{2}+12 x+12 \nonumber \]

In vertex form \[f(x)=2(x+3)^{2}-6 \nonumber \]

the coordinates of the vertex were easily seen to be (−3, −6) (see Figure \(\PageIndex{2}\)). Let’s see what the new formula for the x-coordinate of the vertex reveals.

As usual, compare \(f(x)=2 x^{2}+12 x+12\) with \(f(x)=a x^{2}+b x+c\) and note that a = 2, b = 12 and c = 12. Thus, the x-coordinate of the vertex is given by

\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{12}{2(2)}=-3 \nonumber \]

Note that this agrees with the previous result (see Figure \(\PageIndex{2}\)). We could find the y-coordinate of the vertex with

\[y_{\text { vertex }}=\frac{4 a c-b^{2}}{4 a}=\frac{4(2)(12)-(12)^{2}}{4(2)}=\frac{-48}{8}=-6 \nonumber \]

but we find this formula for the y-coordinate of the vertex a bit hard to memorize. We find it easier to do the following. Since we know the x-coordinate of the vertex is x = −3, we can find the y-coordinate of the vertex by simply substituting x = −3 in the equation of the parabola. That is, with \(f(x)=2 x^{2}+12 x-12\),

\[f(-3)=2(-3)^{2}+12(-3)+12=-6 \nonumber \]

Let’s highlight this last technique.

Finding the y-coordinate of the Vertex

Given the parabola represented by the quadratic function \[f(x)=a x^{2}+b x+c \nonumber \]

we’ve seen that the x-coordinate of the vertex is given by x = −b/(2a). To find the y-coordinate of the vertex, it is probably easiest to evaluate the function at x = −b/(2a). That is, the y-coordinate of the vertex is given by

\[y_{\text { vertex }}=f\left(-\frac{b}{2 a}\right) \nonumber \]

Let’s look at another example.

Example \(\PageIndex{3}\)

Consider the parabola having equation \[f(x)=-2 x^{2}+3 x-8 \nonumber \]

Find the coordinates of the vertex.

Solution

First, use the new formula to find the x-coordinate of the vertex.

\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{3}{2(-2)}=\frac{3}{4} \nonumber \]

Next, substitute x = 3/4 to find the corresponding y-coordinate.

\[\begin{aligned} f\left(\frac{3}{4}\right) &=-2\left(\frac{3}{4}\right)^{2}+3\left(\frac{3}{4}\right)-8 \\ &=-2\left(\frac{9}{16}\right)+\frac{9}{4}-8 \\ &=-\frac{9}{8}+\frac{18}{8}-\frac{64}{8} \\ &=-\frac{55}{8} \end{aligned} \nonumber \]

Thus, the coordinates of the vertex are (3/4, −55/8).

Applications

We’re now in a position to do some applications of optimization. Let’s start with an easy example.

Example \(\PageIndex{4}\)

Find two real numbers x and y that sum to 50 and that have a product that is a maximum.

Solution

Before we apply the theory of the previous examples, let’s just play with the numbers a bit to get a feel for what we are being asked to do. We need to find two numbers that sum to 50, so let’s start with x = 5 and y = 45. Clearly, the sum of these two numbers is 50. On the other hand, their product is xy = (5)(45) = 225. Let’s place this result in a table.

x	y	xy
5	45	225

For a second guess, select x = 10 and y = 40. The sum of these two numbers is 50 and their product is xy = 400. For a third guess, select x = 20 and y = 30. The sum of these two numbers is 50 and their product is xy = 600. Let’s add these results to our table.

x	y	xy
5	45	225
10	40	400
20	30	600

Thus far, the best pair is x = 20 and y = 30, because their product is the maximum in the table above. But is there another pair with a larger product? Remember our goal is to find a pair with a product that is a maximum. That is, our pair must have a product larger than any other pair. Can you find a pair that has a product larger than 600?

Now that we have a feel for what we are being asked to do (find two numbers that sum to 50 and that have a product that is a maximum), let’s try an approach that is more abstract than the “guess and check” approach of our tables. Our first constraint is the fact that the sum of the numbers x and y must be 50. We can model this constraint with the equation

\[x+y=50 \nonumber \]

We’re being asked to maximize the product. Thus, you want to find a formula for the product. Let’s let P represent the product of x and y and write

\[P=x y \nonumber \]

Note that P is a function of two variables x and y. However, all of our functions in this course have thus far been a function of a single variable. So, how can we get rid of one of the variables? Simple, first solve equation (8) for y.

\[\begin{aligned} x+y &=50 \\ y &=50-x \end{aligned} \nonumber \]

Now, substitute equation (10) into the product in equation (9).

\[P=x(50-x) \nonumber \]

or, equivalently,

\[P=-x^{2}+50 x \nonumber \]

Note that P is now a function of a single variable x. Note further that the function defined by equation (11) is quadratic. If we compare \(P=-x^{2}+50 x\) with the general form \(P=a x^{2}+b x+c\), note that a = −1 and b = 50 (we have no need of the fact that c = 0). Therefore, if we plot P versus x, the graph is a parabola that opens downward (see Figure \(\PageIndex{3}\)) and the maximum value of P will occur at the vertex. The x-coordinate of the vertex is found with

\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{50}{2(-1)}=25 \nonumber \]

Figure \(\PageIndex{3}\). The maximum product P=625 occurs at the vertex of the parabola, (25, 625).

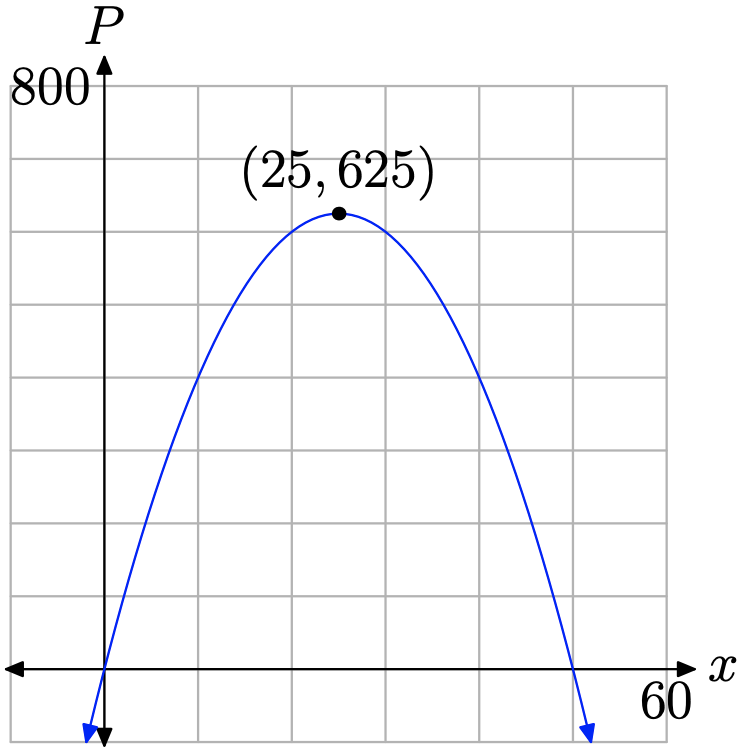
Thus, our first number is x = 25. We can find the second number y by substituting x = 25 in equation (10).

\[y=50-x=50-25=25 \nonumber \]

Note that the sum of x and y is x + y = 25 + 25 = 50. There are two ways that we can find their product. Since we now know the numbers x and y, we can multiply to find P = xy = (25)(25) = 625. Alternatively, we could substitute x = 25 in equation (11) to get

\[P=-x^{2}+50 x=-(25)^{2}+50(25)=-625+1250=625 \nonumber \]

When you compare this result with our experimental tables, things come together. We’ve found two numbers x and y that sum to 50 with a product that is a maximum. No other numbers that sum to 50 have a larger product.

Our little formula \(x_{\text { vertex }}=-b /(2 a)\) has proven to be a powerful ally. Let’s try another example.

Example \(\PageIndex{5}\)

Find two real numbers with a difference of 8 such that the sum of the squares of the two numbers is a minimum.

Solution

Let’s begin by letting x and y represent the numbers we seek. Next, let’s play a bit as we did in the previous example. Try x = 9 and y = 1. The difference of these two numbers is certainly 8. The sum of the squares of these two numbers is \(S=9^{2}+1^{2}=82\). Let’s put this result in tabular form.

x	y	\(S=x^{2}+y^{2}\)
9	1	82

For a second guess, select x = 8 and y = 0. The difference is x − y = 8 − 0 = 8, but this time the sum of the squares is \(S=8^{2}+0^{2}=64\). For a third guess, try x = 7 and y = −1. Again, the difference is x − y = 7 − (−1) = 8, but the sum of the squares is now \(S=7^{2}+(-1)^{2}=50\). Let’s add these results to our table.

x	y	\(S=x^{2}+y^{2}\)
9	1	82
8	0	64
7	-1	50

Thus far, the pair that minimizes the sum of the squares is x = 7 and y = −1. However, could there be another pair with a difference of 8 and the sum of the squares is smaller than 50? Experiment further to see if you can best the current minimum of 50.

Let’s try an analytical approach. Our first constraint is the fact that the difference of the two numbers must equal 8. This is easily expressed as

\[x-y=8 \nonumber \]

Next, we’re asked to minimize the sum of the squares of the two numbers. This requires that we find a formula for the sum of the squares. Let S represent the sum of the squares of x and y. Thus,

\[S=x^{2}+y^{2} \nonumber \]

Note that S is a function of two variables. We can eliminate one of the variables by solving equation (13) for x, \[x=y+8 \nonumber \]

then substituting this result in equation (14).

\[S=(y+8)^{2}+y^{2} \nonumber \]

Expand and simplify. \[S=2 y^{2}+16 y+64 \nonumber \]

Compare \(S=2 y^{2}+16 y+64\) with the general quadratic \(S=a y^{2}+b y+c\) and note that a = 2 and b = 16. Thus, the plot of S versus y will be a parabola that opens upward (see Figure \(\PageIndex{4}\)) and the minimum value of S will occur at the vertex. The y-coordinate of the vertex is found with

\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{16}{2(2)}=-4 \nonumber \]

Figure \(\PageIndex{4}\) Plotting the sum of the squares S versus y. The minimum S, 32, occurs at the vertex, (−4, 32).

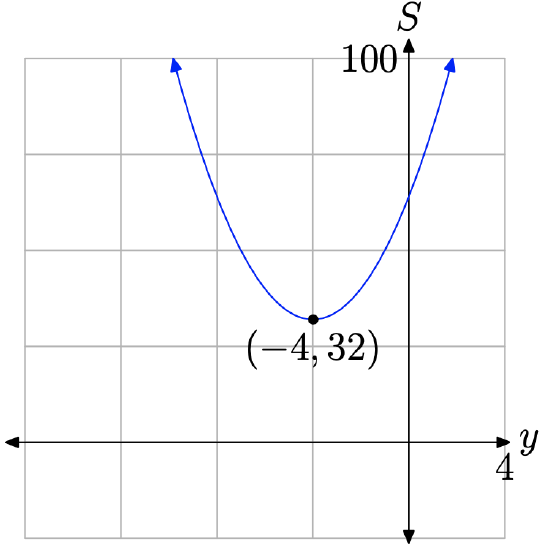
Thus, the first number we seek is y = −4. We can find the second number by substituting y = −4 in equation (15).

\[x=y+8=(-4)+8=4 \nonumber \]

Hence, the numbers we seek are x = 4 and y = −4. Note that the difference of these two numbers is x−y = 4−(−4) = 8 and the sum of their squares is \(S=(4)^{2}+(-4)^{2}=32\), which is smaller than the best result found in our tabular experiment above. Indeed, our work show that this is the smallest possible value of S.

Alternatively, you can find S by substituting y = −4 in equation (16). We’ll leave it to our readers to verify that this also gives a minimum value of S = 32.

Let’s look at another application.

Example \(\PageIndex{6}\)

Mary wants to fence a rectangular garden to keep the deer from eating her fruit and vegetables. One side of her garden abuts her shed wall so she will not need to fence that side. However, she also wants to use material to separate the rectangular garden in two sections (see Figure \(\PageIndex{5}\)). She can afford to buy 80 total feet of fencing to use for the perimeter and the section dividing the rectangular garden. What dimensions will maximize the total area of the rectangular garden?

Figure \(\PageIndex{5}\) Mary’s rectangular garden needs fencing on three sides and also for the fence to divide the garden.

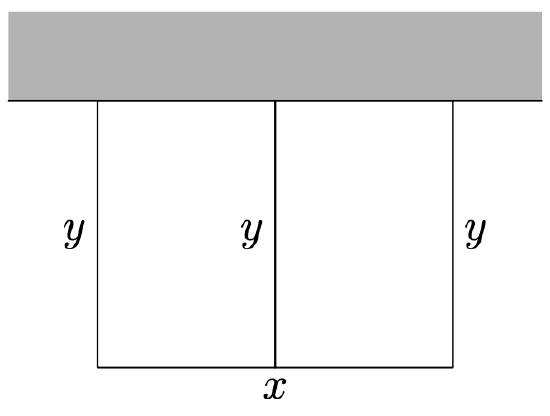
Solution

Again, before we take an algebraic approach, let’s just experiment. Note that we’ve labeled the width with the letter x and the height with the letter y in our sketch of the garden in Figure \(\PageIndex{5}\).

There is a total of 80 feet of fence material. Suppose that we let y = 5 ft. Because there are three sides of length y = 5 ft, we’ve used 15 feet of material. That leaves 65 feet of material which will be used to fence the width of the garden. That is, the width is x = 65 ft. Thus, the dimensions of the garden are x = 65 ft by y = 5 ft. The area equals the product of these two measures, so \(A=325 \mathrm{ft}^{2}\). Let’s put this result into a table.

x	y	A=xy
65 ft	5 ft	325 \(\text{ft}^{2}\)

Suppose instead that we let the height be y = 10 ft. Again, there are three sections with this length, so this will take 30 ft of material. That leaves 50 ft of material, so the width x = 50 ft. The area is the product of these two measures, so \(A=500 \mathrm{ft}^{2}\). As a third experiment, let the height y = 15 ft. Subtracting three of these lengths from 80 ft, we see that the width x = 35 ft. The area is the product of these measures, so \(A=525 \mathrm{ft}^{2}\). Let’s add these last two number experiments to our table.

x	y	A=xy
65 ft	5 ft	325 \(\text{ft}^{2}\)
50 ft	10 ft	500 \(\text{ft}^{2}\)
35 ft	15 ft	525 \(\text{ft}^{2}\)

At this point, the last set of dimensions yields the maximum area, but is it possible that another choice of x and y will yield a larger area? Experiment further with numbers of your choice to see if you can find dimensions that will yield an area larger than the current maximum in the table, namely 525 \(\mathrm{ft}^{2}\).

Let’s now call on what we’ve learned in this section to attack this model. First, we’re constrained by the amount of material we have for the job, a total of 80 ft of fencing. This constraint requires that 3 times the height of the garden, added to the width of the garden, should equal the available amount of fencing material. In symbols,

\[x+3 y=80 \nonumber \]

We’re asked to maximize the area, so we focus our efforts on finding a formula for the area of the rectangular garden. Because the area A of the rectangular garden is the product of the width and the height, \[A=x y \nonumber \]

We now have a formula for the area of the rectangular garden, but unfortunately we have the area A as a function of two variables. We need to eliminate one or the other of these variables. This is easily done by solving equation (18) for x. \[x=80-3 y \nonumber \]

Next, substitute this result in equation (19) to get \[A=(80-3 y) y \nonumber \]

or, equivalently, \[A=-3 y^{2}+80 y \nonumber \]

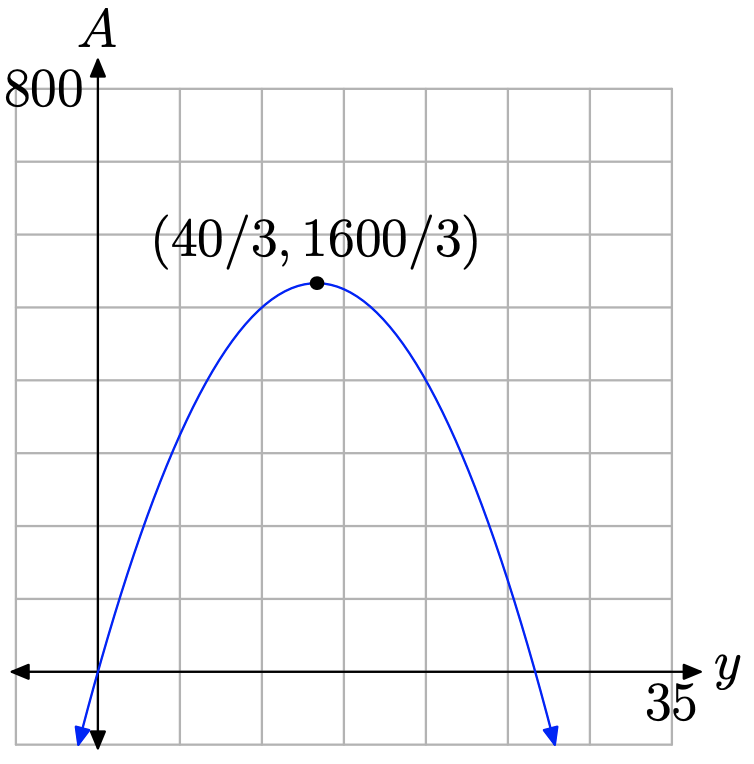
Note that we have expressed the area A as a function of a single variable y. Also, the function defined by equation (21) is quadratic. Compare \(A=-3 y^{2}+80 y\) with the general form \(A=a y^{2}+b y+c\) and note that a = −3 and b = 80 (we have no need of the fact that c = 0). Therefore, if we plot A versus y, the graph is a parabola that opens downward (see Figure \(\PageIndex{6}\)), so the maximum value of A will occur at the vertex. The y-coordinate of the vertex is found with

\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{80}{2(-3)}=\frac{80}{6}=\frac{40}{3} \nonumber \]

To find the width of the rectangular garden, substitute y = 40/3 into equation (20) and solve for x.

\[x=80-3 y=80-3\left(\frac{40}{3}\right)=80-40=40 \nonumber \]

Thus, the width of the rectangular garden is 40 ft. We can find the area of the garden by multiplying the width and the height.

\[A=x y=(40)\left(\frac{40}{3}\right)=\frac{1600}{3}=533 \frac{1}{3} \nonumber \]

Note that the resulting area, \(A=533 \frac{1}{3} \mathrm{ft}^{2}\), is only slightly bigger the last tabular entry found with our numerical experiments.

You can also find the area of the rectangular region by substituting y = 40/3 into equation (21). We’ll leave it to our readers to check that this provides the same measure for the area. You will also notice that the second coordinate of the vertex in Figure \(\PageIndex{6}\) is the maximum area \(A=1600 / 3 \mathrm{ft}^{2}\).

Figure \(\PageIndex{6}\). The maximum area, A=1600\(/ 3 \mathrm{ft}^{2}\), occurs at the vertex of the parabola, (40/3, 1600/3).

Exercise

Exercise \(\PageIndex{1}\)

Find the exact maximum value of the function \(f(x) = −x^2−3x\).

Answer

\(\frac{9}{4}\)

Exercise \(\PageIndex{2}\)

Find the exact maximum value of the function \(f(x) = −x^2−5x−2\).

Exercise \(\PageIndex{3}\)

Find the vertex of the graph of the function \(f(x) = −3x^2−x−6\).

Answer

\((−\frac{1}{6}, −\frac{71}{12})\)

Exercise \(\PageIndex{4}\)

Find the range of the function \(f(x) = −2x^2−9x+2\).

Exercise \(\PageIndex{5}\)

Find the exact maximum value of the function \(f(x) = −3x^2−9x−4\).

Answer

\(\frac{11}{4}\)

Exercise \(\PageIndex{6}\)

Find the equation of the axis of symmetry of the graph of the function \(f(x) = −x^2−5x−9\).

Exercise \(\PageIndex{7}\)

Find the vertex of the graph of the function \(f(x) = 3x^2+3x+9\).

Answer

\((−\frac{1}{2}, \frac{33}{4})\)

Exercise \(\PageIndex{8}\)

Find the exact minimum value of the function \(f(x) = x^2+x+1\).

Exercise \(\PageIndex{9}\)

Find the exact minimum value of the function \(f(x) = x^2+9x\).

Answer

\(−\frac{81}{4}\)

Exercise \(\PageIndex{10}\)

Find the range of the function \(f(x) = 5x^2−3x−4\).

Exercise \(\PageIndex{11}\)

Find the range of the function \(f(x) = −3x^2+8x−2\).

Answer

\((−\infty, \frac{10}{3}]\) = {\(x|x \le \frac{10}{3}\)}

Exercise \(\PageIndex{12}\)

Find the exact minimum value of the function \(f(x) = 2x^2+5x−6\).

Exercise \(\PageIndex{13}\)

Find the range of the function \(f(x) = 4x^2+9x−8\).

Answer

\([−\frac{209}{16}, \infty)\) = {\(x|x \ge −\frac{209}{16}\)}

Exercise \(\PageIndex{14}\)

Find the exact maximum value of the function \(f(x) = −3x^2−8x−1\).

Exercise \(\PageIndex{15}\)

Find the equation of the axis of symmetry of the graph of the function \(f(x) = −4x^2−2x+9\).

Answer

\(x = −\frac{1}{4}\)

Exercise \(\PageIndex{16}\)

Find the exact minimum value of the function \(f(x) = 5x^2+2x−3\).

Exercise \(\PageIndex{17}\)

A ball is thrown upward at a speed of 8 ft/s from the top of a 182 foot high building. How many seconds does it take for the ball to reach its maximum height? Round your answer to the nearest hundredth of a second.

Answer

0.25

Exercise \(\PageIndex{18}\)

A ball is thrown upward at a speed of 9 ft/s from the top of a 143 foot high building. How many seconds does it take for the ball to reach its maximum height? Round your answer to the nearest hundredth of a second.

Exercise \(\PageIndex{19}\)

A ball is thrown upward at a speed of 52 ft/s from the top of a 293 foot high building. What is the maximum height of the ball? Round your answer to the nearest hundredth of a foot.

Answer

335.25

Exercise \(\PageIndex{20}\)

A ball is thrown upward at a speed of 23 ft/s from the top of a 71 foot high building. What is the maximum height of the ball? Round your answer to the nearest hundredth of a foot.

Exercise \(\PageIndex{21}\)

Find two numbers whose sum is 20 and whose product is a maximum.

Answer

10 and 10

Exercise \(\PageIndex{22}\)

Find two numbers whose sum is 36 and whose product is a maximum.

Exercise \(\PageIndex{23}\)

Find two numbers whose difference is 12 and whose product is a minimum.

Answer

6 and −6

Exercise \(\PageIndex{24}\)

Find two numbers whose difference is 24 and whose product is a minimum.

Exercise \(\PageIndex{25}\)

One number is 3 larger than twice a second number. Find two such numbers so that their product is a minimum.

Answer

\(\frac{3}{2}\) and \(−\frac{3}{4}\)

Exercise \(\PageIndex{26}\)

One number is 2 larger than 5 times a second number. Find two such numbers so that their product is a minimum.

Exercise \(\PageIndex{27}\)

Among all pairs of numbers whose sum is −10, find the pair such that the sum of their squares is the smallest possible.

Answer

−5, −5

Exercise \(\PageIndex{28}\)

Among all pairs of numbers whose sum is −24, find the pair such that the sum of their squares is the smallest possible.

Exercise \(\PageIndex{29}\)

Among all pairs of numbers whose sum is 14, find the pair such that the sum of their squares is the smallest possible.

Answer

7, 7

Exercise \(\PageIndex{30}\)

Among all pairs of numbers whose sum is 12, find the pair such that the sum of their squares is the smallest possible.

Exercise \(\PageIndex{31}\)

Among all rectangles having perimeter 40 feet, find the dimensions (length and width) of the one with the greatest area.

Answer

10 feet by 10 feet

Exercise \(\PageIndex{32}\)

Among all rectangles having perimeter 100 feet, find the dimensions (length and width) of the one with the greatest area.

Exercise \(\PageIndex{33}\)

A farmer with 1700 meters of fencing wants to enclose a rectangular plot that borders on a river. If no fence is required along the river, what is the largest area that can be enclosed?

Answer

361250 square meters

Exercise \(\PageIndex{34}\)

A rancher with 1500 meters of fencing wants to enclose a rectangular plot that borders on a river. If no fence is required along the river, and the side parallel to the river is x meters long, find the value of x which will give the largest area of the rectangle.

Exercise \(\PageIndex{35}\)

A park ranger with 400 meters of fencing wants to enclose a rectangular plot that borders on a river. If no fence is required along the river, and the side parallel to the river is x meters long, find the value of x which will give the largest area of the rectangle.

Answer

200

Exercise \(\PageIndex{36}\)

A rancher with 1000 meters of fencing wants to enclose a rectangular plot that borders on a river. If no fence is required along the river, what is the largest area that can be enclosed?

Exercise \(\PageIndex{37}\)

Let x represent the demand (the number the public will buy) for an object and let p represent the object’s unit price (in dollars). Suppose that the unit price and the demand are linearly related by the equation \(p = −\frac{1}{3}x + 40\).

1. Express the revenue R (the amount earned by selling the objects) as a function of the demand x.
2. Find the demand that will maximize the revenue.
3. Find the unit price that will maximize the revenue.
4. What is the maximum revenue?

Answer

1. \(R = −\frac{1}{3}x^2+40x\)
2. x = 60 objects
3. p = 20 dollars
4. R = $1200

Exercise \(\PageIndex{38}\)

Let x represent the demand (the number the public will buy) for an object and let p represent the object’s unit price (in dollars). Suppose that the unit price and the demand are linearly related by the equation \(p = −\frac{1}{5}x + 200\).

1. Express the revenue R (the amount earned by selling the objects) as a function of the demand x.
2. Find the demand that will maximize the revenue.
3. Find the unit price that will maximize the revenue.
4. What is the maximum revenue?

Exercise \(\PageIndex{39}\)

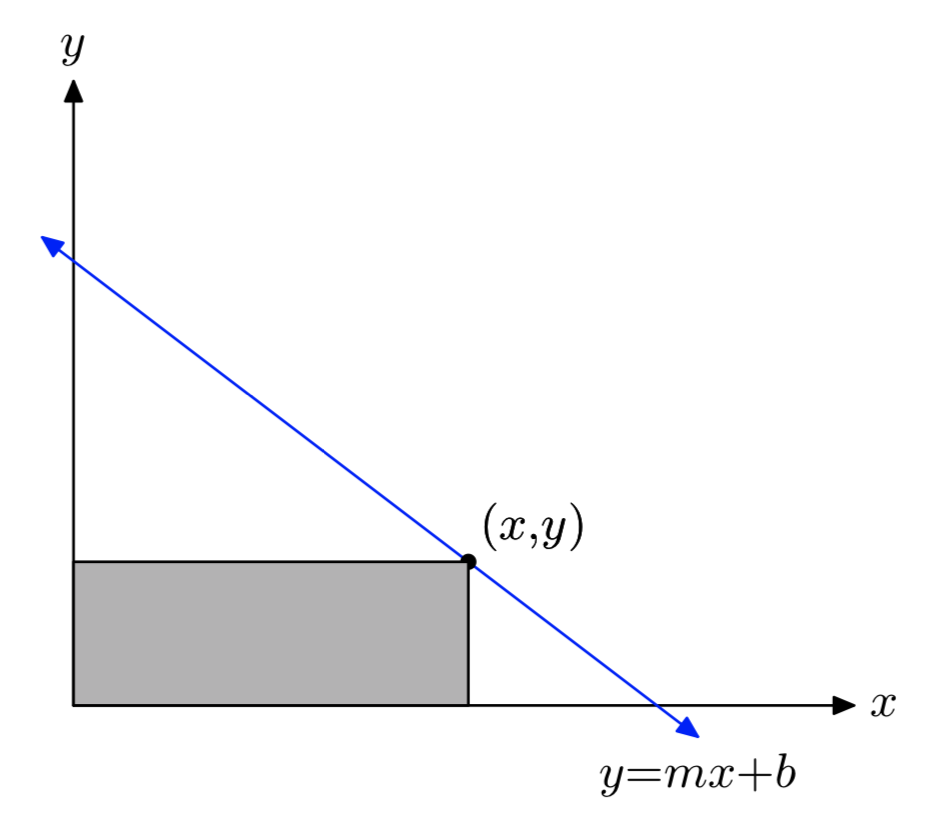
A point from the first quadrant is selected on the line y = mx + b. Lines are drawn from this point parallel to the axes to form a rectangle under the line in the first quadrant. Among all such rectangles, find the dimensions of the rectangle with maximum area. What is the maximum area? Assume m < 0.

Answer

\(x = −\frac{b}{2m}\),

\(y = \frac{b}{2}\),

\(A = −\frac{b^2}{4m}\)

Exercise \(\PageIndex{40}\)

A rancher wishes to fence a rectangular area. The east-west sides of the rectangle will require stronger support due to prevailing east-west storm winds. Consequently, the cost of fencing for the east-west sides of the rectangular area is $18 per foot. The cost for fencing the north-south sides of the rectangular area is $12 per foot. Find the dimension of the largest possible rectangular area that can be fenced for $7200.