5.2: Vertex Form
- Page ID
- 19707
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the previous section, you learned that it is a simple task to sketch the graph of a quadratic function if it is presented in vertex form
\[f(x)=a(x-h)^{2}+k \nonumber \]
The goal of the current section is to start with the most general form of the quadratic function, namely
\[f(x)=a x^{2}+b x+c \nonumber \]
and manipulate the equation into vertex form. Once you have your quadratic function in vertex form, the technique of the previous section should allow you to construct the graph of the quadratic function. However, before we turn our attention to the task of converting the general quadratic into vertex form, we need to review the necessary algebraic fundamentals. Let’s begin with a review of an important algebraic shortcut called squaring a binomial.
Squaring a Binomial
A monomial is a single algebraic term, usually constructed as a product of a number (called a coefficient) and one or more variables raised to nonnegative integral powers, such as \(-3 x^{2}\) or 14\(y^{3} z^{5}\). The key phrase here is “single term.” A binomial is an algebraic sum or difference of two monomials (or terms), such as \(x+2 y\) or \(3 a b^{2}-2 c^{3}\). The key phrase here is “two terms.”
To “square a binomial,” start with an arbitrary binomial, such as a+b, then multiply it by itself to produce its square (a + b)(a + b), or, more compactly, \((a+b)^{2}\). We can use the distributive property to expand the square of the binomial a + b.
\[\begin{aligned}(a+b)^{2} &=(a+b)(a+b) \\ &=a(a+b)+b(a+b) \\ &=a^{2}+a b+b a+b^{2} \end{aligned} \nonumber \]
Because ab = ba, we can add the two middle terms to arrive at the following property.
The square of the binomial a + b is expanded as follows.
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber \]
Expand \((x+4)^{2}\)
Solution
We could proceed as follows.
\[\begin{align*}(x+4)^{2} &=(x+4)(x+4) \\ &=x(x+4)+4(x+4) \\ &=x^{2}+4 x+4 x+16 \\ &=x^{2}+8 x+16 \end{align*} \]
Although correct, this technique will not help us with our upcoming task. What we need to do is follow the algorithm suggested by Property 3.
To square the binomial a + b, proceed as follows:
- Square the first term to get \(a^2\).
- Multiply the first and second terms together, and then multiply the result by two to get 2ab.
- Square the second term to get \(b^2\).
Thus, to expand \((x + 4)^2\), we should proceed as follows.
- Square the first term to get \(x^2\)
- Multiply the first and second terms together and then multiply by two to get 8x.
- Square the second term to get 16.
Proceeding in this manner allows us to perform the expansion mentally and simply write down the solution.
\[(x+4)^{2}=x^{2}+2(x)(4)+4^{2}=x^{2}+8 x+16 \nonumber \]
Here are a few more examples. In each, we’ve written an extra step to help clarify the procedure. In practice, you should simply write down the solution without any intermediate steps.
\[\begin{array}{l}{(x+3)^{2}=x^{2}+2(x)(3)+3^{2}=x^{2}+6 x+9} \\ {(x-5)^{2}=x^{2}+2(x)(-5)+(-5)^{2}=x^{2}-10 x+25} \\ {\left(x-\frac{1}{2}\right)^{2}=x^{2}+2(x)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)^{2}=x^{2}-x+\frac{1}{4}}\end{array} \nonumber \]
It is imperative that you master this shortcut before moving on to the rest of the material in this section.
Perfect Square Trinomials
Once you’ve mastered squaring a binomial, as in
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber \]
it’s a simple matter to identify and factor trinomials (three terms) having the form \(a^{2}+2 a b+b^{2}\). You simply “undo” the multiplication. Whenever you spot a trinomial whose first and third terms are perfect squares, you should suspect that it factors as follows.
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \nonumber \]
A trinomial that factors according to this rule or pattern is called a perfect square trinomial.
For example, the first and last terms of the following trinomial are perfect squares.
\[x^{2}+16 x+64 \nonumber \]
The square roots of the first and last terms are x and 8, respectively. Hence, it makes sense to try the following.
\[x^{2}+16 x+64=(x+8)^{2} \nonumber \]
It is important that you check your result using multiplication. So, following the three-step algorithm for squaring a binomial:
- Square x to get \(x^2\).
- Multiply x and 8 to get 8x, then multiply this result by 2 to get 16x.
- Square 8 to get 64.
Hence, \(x^2 + 16x + 64\) is a perfect square trinomial and factors as \((x + 8)^2\).
As another example, consider \(x^2 − 10x + 25\). The square roots of the first and last terms are x and 5, respectively. Hence, it makes sense to try
\[x^{2}-10 x+25=(x-5)^{2} \nonumber \]
Again, you should check this result. Note especially that twice the product of x and −5 equals the middle term on the left, namely, −10x.
Completing the Square
If a quadratic function is given in vertex form, it is a simple matter to sketch the parabola represented by the equation. For example, consider the quadratic function
\[f(x)=(x+2)^{2}+3 \nonumber \]
which is in vertex form. The graph of this equation is a parabola that opens upward. It is translated 2 units to the left and 3 units upward. This is the advantage of vertex form. The transformations required to draw the graph of the function are easy to spot when the equation is written in vertex form.
It’s a simple matter to transform the equation \(f(x) = (x + 2)^2 + 3\) into the general form of a quadratic function, \(f(x) = ax^2 + bx + c\). We simply use the three-step algorithm to square the binomial; then we combine like terms.
\[\begin{array}{l}{f(x)=(x+2)^{2}+3} \\ {f(x)=x^{2}+4 x+4+3} \\ {f(x)=x^{2}+4 x+7}\end{array} \nonumber \]
Note, however, that the result of this manipulation, \(f(x) = x^2 + 4x+ 7\), is not as useful as vertex form, as it is difficult to identify the transformations required to draw the parabola represented by the equation \(f(x) = x^2 + 4x + 7\).
It’s really the reverse of the manipulation above that is needed. If we are presented with an equation in the form \(f(x) = ax^2 + bx + c\), such as \(f(x) = x^2 + 4x + 7\), then an algebraic method is needed to convert this equation to vertex form \(f(x) = a(x−h)^2+k\); or in this case, back to its original vertex form \(f(x) = (x + 2)^2 + 3\).
The procedure we seek is called completing the square. The name is derived from the fact that we need to “complete” the trinomial on the right side of \(y = x^2 + 4x + 7\) so that it becomes a perfect square trinomial.
The procedure for completing the square involves three key steps.
- Take half of the coefficient of x and square the result.
- Add and subtract the quantity from step one so that the right-hand side of the equation does not change.
- Factor the resulting perfect square trinomial and combine constant terms.
Let’s follow this procedure and place \(f(x) = x^2 + 4x + 7\) in vertex form.
- Take half of the coefficient of x. Thus, (1/2)(4) = 2. Square this result. Thus, \(2^2 = 4\).
- Add and subtract 4 on the right side of the equation \(f(x) = x^2 + 4x + 7\) \[f(x)=x^{2}+4 x+4-4+7 \nonumber \]
- Group the first three terms on the right-hand side. These form a perfect square trinomial.
\[f(x)=\left(x^{2}+4 x+4\right)-4+7 \nonumber \]
Now factor the perfect square trinomial and combine the constants at the end to get
\[f(x)=(x+2)^{2}+3 \nonumber \]
That’s it, we’re done! We’ve returned the general quadratic \(f(x) = x^2 + 4x + 7\) back to vertex form \(f(x) = (x + 2)^2 + 3\).
Let’s try that once more.
Place the quadratic function \(f(x) = x^2 − 8x − 9\) in vertex form.
Solution
We follow the three-step algorithm for completing the square.
- Take half of the coefficient of x and square: i.e., \[[(1 / 2)(-8)]^{2}=[-4]^{2}=16 \nonumber \]
- Add and subtract this amount to the right-hand side of the function. \[f(x)=x^{2}-8 x+16-16-9 \nonumber \]
- Group the first three terms on the right-hand side. These form a perfect square trinomial. \[f(x)=\left(x^{2}-8 x+16\right)-16-9 \nonumber \]
Factor the perfect square trinomial and combine the coefficients at the end.
\[f(x)=(x-4)^{2}-25 \nonumber \]
Now, let’s see how we can use the technique of completing the square to help in drawing the graphs of general quadratic functions.
Working with \(f(x) = x^2 + bx + c\)
The examples in this section will have the form \(f(x) = x^2 + bx + c\). Note that the coefficient of \(x^2\) is 1. In the next section, we will work with a harder form, \(f(x) = ax^2 + bx + c\), where \(a \neq 1\).
Complete the square to place \(f(x) = x^2 + 6x + 2\) in vertex form and sketch its graph.
Solution
First, take half of the coefficient of x and square; i.e., \([(1/2)(6)]^2 = 9\). On the right side of the equation, add and subtract this amount so as to not change the equation.
\[f(x)=x^{2}+6 x+9-9+2 \nonumber \]
Group the first three terms on the right-hand side.
\[f(x)=\left(x^{2}+6 x+9\right)-9+2 \nonumber \]
The first three terms on the right-hand side form a perfect square trinomial that is easily factored. Also, combine the constants at the end.
\[f(x)=(x+3)^{2}-7 \nonumber \]
This is a parabola that opens upward. We need to shift the parabola 3 units to the left and then 7 units downward, placing the vertex at (−3, −7) as shown in Figure \(\PageIndex{1}\)(a). The axis of symmetry is the vertical line x = −3. The table in Figure \(\PageIndex{1}\)(b) calculates two points to the right of the axis of symmetry, and mirror points on the left of the axis of symmetry make for an accurate plot of the parabola.
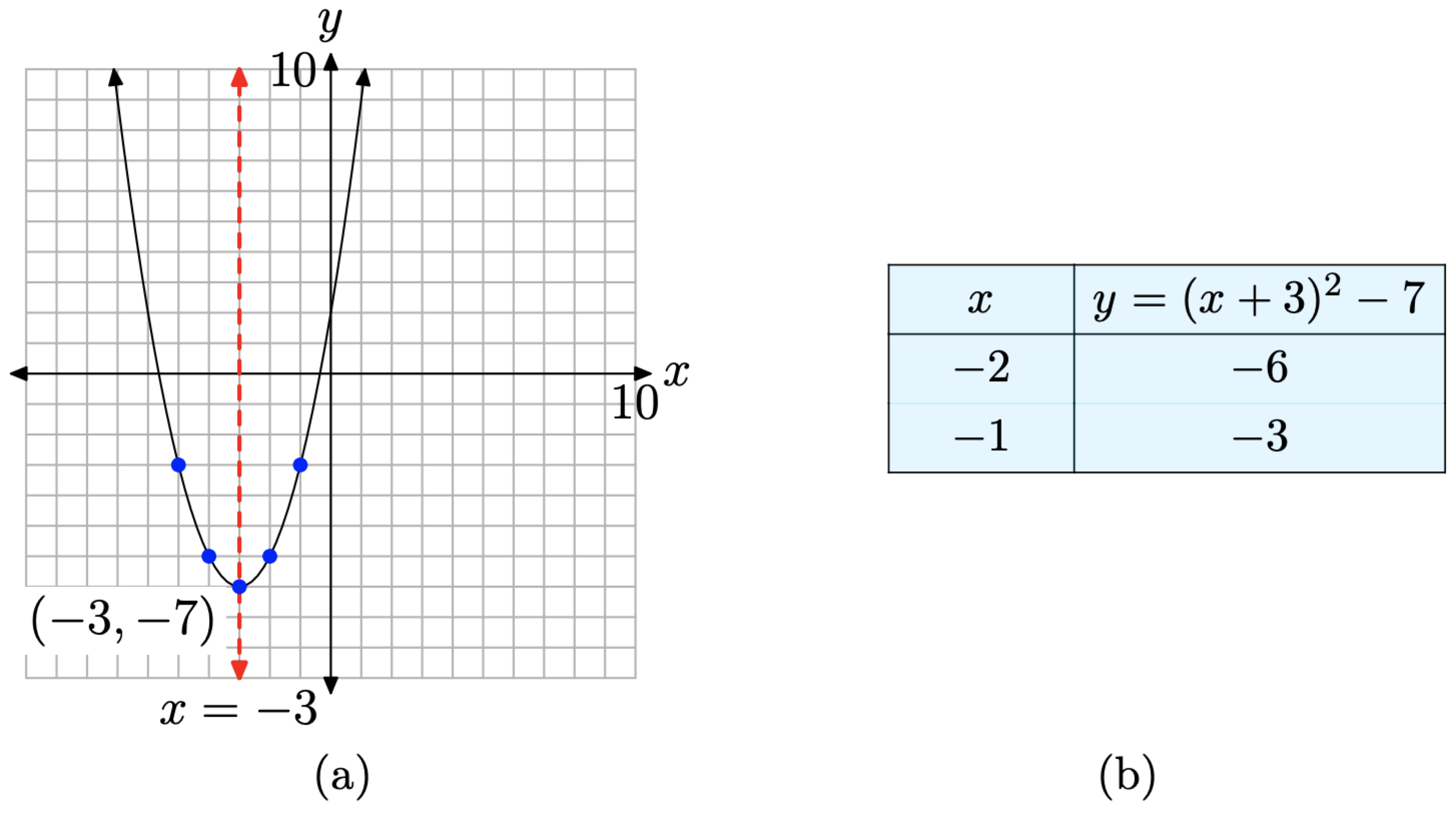
Let’s look at another example.
Complete the square to place \(f(x) = x^2 − 8x + 21\) in vertex form and sketch its graph.
Solution
First, take half of the coefficient of x and square; i.e., \([(1/2)(−8)]^2 = 16\). On the right side of the equation, add and subtract this amount so as to not change the equation.
\[f(x)=x^{2}-8 x+16-16+21 \nonumber \]
Group the first three terms on the right-hand side of the equation.
\[f(x)=\left(x^{2}-8 x+16\right)-16+21 \nonumber \]
The first three terms form a perfect square trinomial that is easily factored. Also, combine constants at the end.
\[f(x)=(x-4)^{2}+5 \nonumber \]
This is a parabola that opens upward. We need to shift the parabola 4 units to the right and then 5 units upward, placing the vertex at (4, 5), as shown in Figure \(\PageIndex{2}\)(a). The table in Figure \(\PageIndex{2}\)(b) calculates two points to the right of the axis of symmetry, and mirror points on the left of the axis of symmetry make for an accurate plot of the parabola.
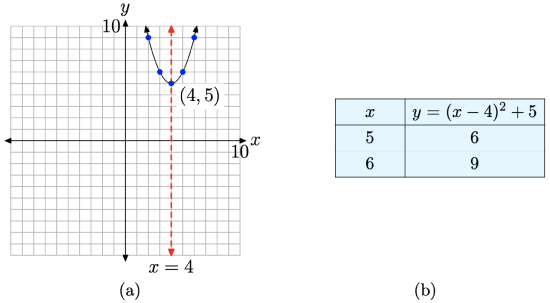
Working with \(f(x) = ax^2 + bx + c\)
In the last two examples, the coefficient of \(x^2\) was 1. In this section, we will learn how to complete the square when the coefficient of \(x^2\) is some number other than 1.
Complete the square to place \(f(x)=2 x^{2}+4 x-4\) in vertex form and sketch its graph.
Solution
In the last two examples, we gained some measure of success when the coefficient of \(x^2\) was a 1. We were just getting comfortable with that situation and we’d like to continue to be comfortable, so let’s start by factoring a 2 from each term on the right-hand side of the equation.
\[f(x)=2\left[x^{2}+2 x-2\right] \nonumber \]
If we ignore the factor of 2 out front, the coefficient of \(x^2\) in the trinomial expression inside the parentheses is a 1. Ah, familiar ground! We will proceed as we did before, but we will carry the factor of 2 outside the parentheses in each step. Start by taking half of the coefficient of x and squaring the result; i.e., \([(1/2)(2)]^2 = 1\).
Add and subtract this amount inside the parentheses so as to not change the equation.
\[f(x)=2\left[x^{2}+2 x+1-1-2\right] \nonumber \]
Group the first three terms inside the parentheses and combine constants.
\[f(x)=2\left[\left(x^{2}+2 x+1\right)-3\right] \nonumber \]
The grouped terms inside the parentheses form a perfect square trinomial that is easily factored.
\[f(x)=2\left[(x+1)^{2}-3\right] \nonumber \]
Finally, redistribute the 2.
\[f(x)=2(x+1)^{2}-6 \nonumber \]
This is a parabola that opens upward. In addition, it is stretched by a factor of 2, so it will be somewhat narrower than our previous examples. The parabola is also shifted 1 unit to the left, then 6 units downward, placing the vertex at (−1, −6), as shown in Figure \(\PageIndex{3}\)(a). The table in Figure \(\PageIndex{3}\)(b) calculates two points to the right of the axis of symmetry, and mirror points on the left of the axis of symmetry make for an accurate plot of the parabola.
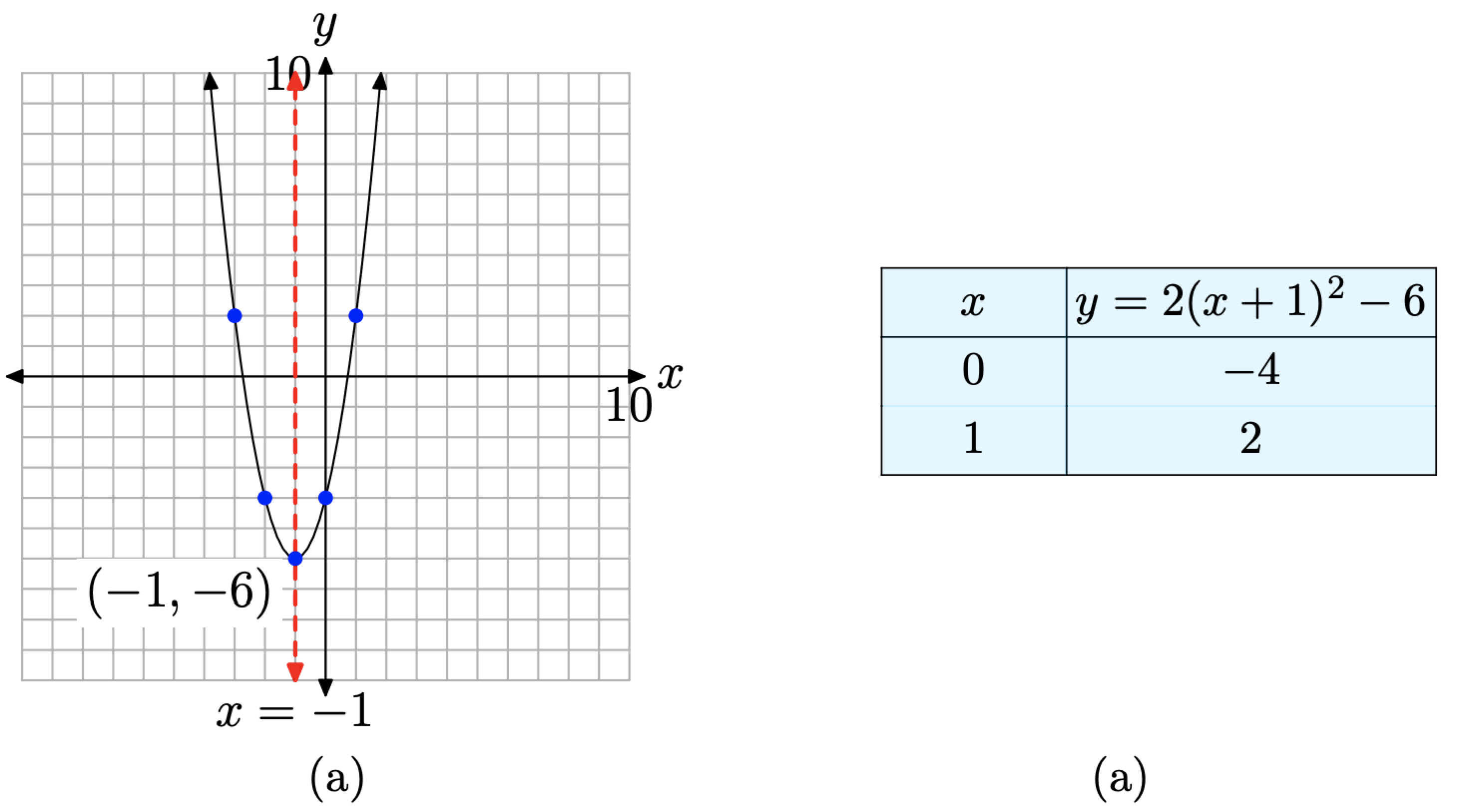
Let’s look at an example where the coefficient of \(x^2\) is negative.
Complete the square to place \(f(x) = −x^2 + 6x − 2\) in vertex form and sketch its graph.
Solution
In the last example, we factored out the coefficient of \(x^2\). This left us with a trinomial having leading coefficient 1, which enabled us to proceed much as we did before: halve the middle coefficient and square, add and subtract this amount, factor the resulting perfect square trinomial. Since we were successful with this technique in the last example, let’s begin again by factoring out the leading coefficient, in this case a −1.
\[f(x)=-1\left[x^{2}-6 x+2\right] \nonumber \]
If we ignore the factor of −1 out front, the coefficient of \(x^2\) in the trinomial expression inside the parentheses is a 1. Again, familiar ground! We will proceed as we did before, but we will carry the factor of −1 outside the parentheses in each step. Start by taking half of the coefficient of x and squaring the result; i.e., \([(1/2)(−6)]^2 = 9\).
Add and subtract this amount inside the parentheses so as to not change the equation.
\[f(x)=-1\left[x^{2}-6 x+9-9+2\right] \nonumber \]
Group the first three terms inside the parentheses and combine constants.
\[f(x)=-1\left[\left(x^{2}-6 x+9\right)-7\right] \nonumber \]
The grouped terms inside the parentheses form a perfect square trinomial that is easily factored.
\[f(x)=-1\left[(x-3)^{2}-7\right] \nonumber \]
Finally, redistribute the −1.
\[f(x)=-(x-3)^{2}+7 \nonumber \]
This is a parabola that opens downward. The parabola is also shifted 3 units to the right, then 7 units upward, placing the vertex at (3, 7), as shown in Figure \(\PageIndex{4}\)(a). The table in Figure \(\PageIndex{4}\)(b) calculates two points to the right of the axis of symmetry, and mirror points on the left of the axis of symmetry make for an accurate plot of the parabola.
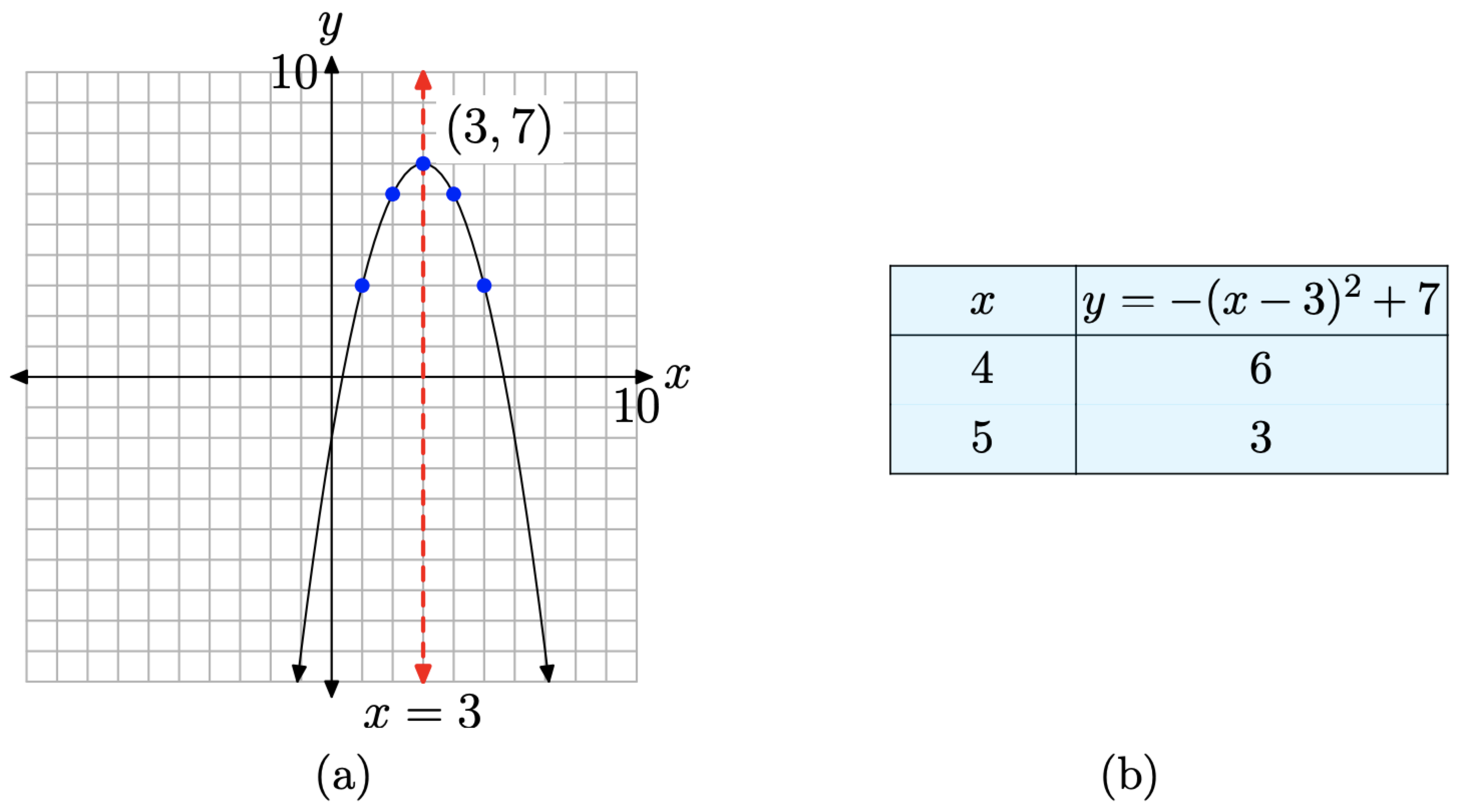
Let’s try one more example.
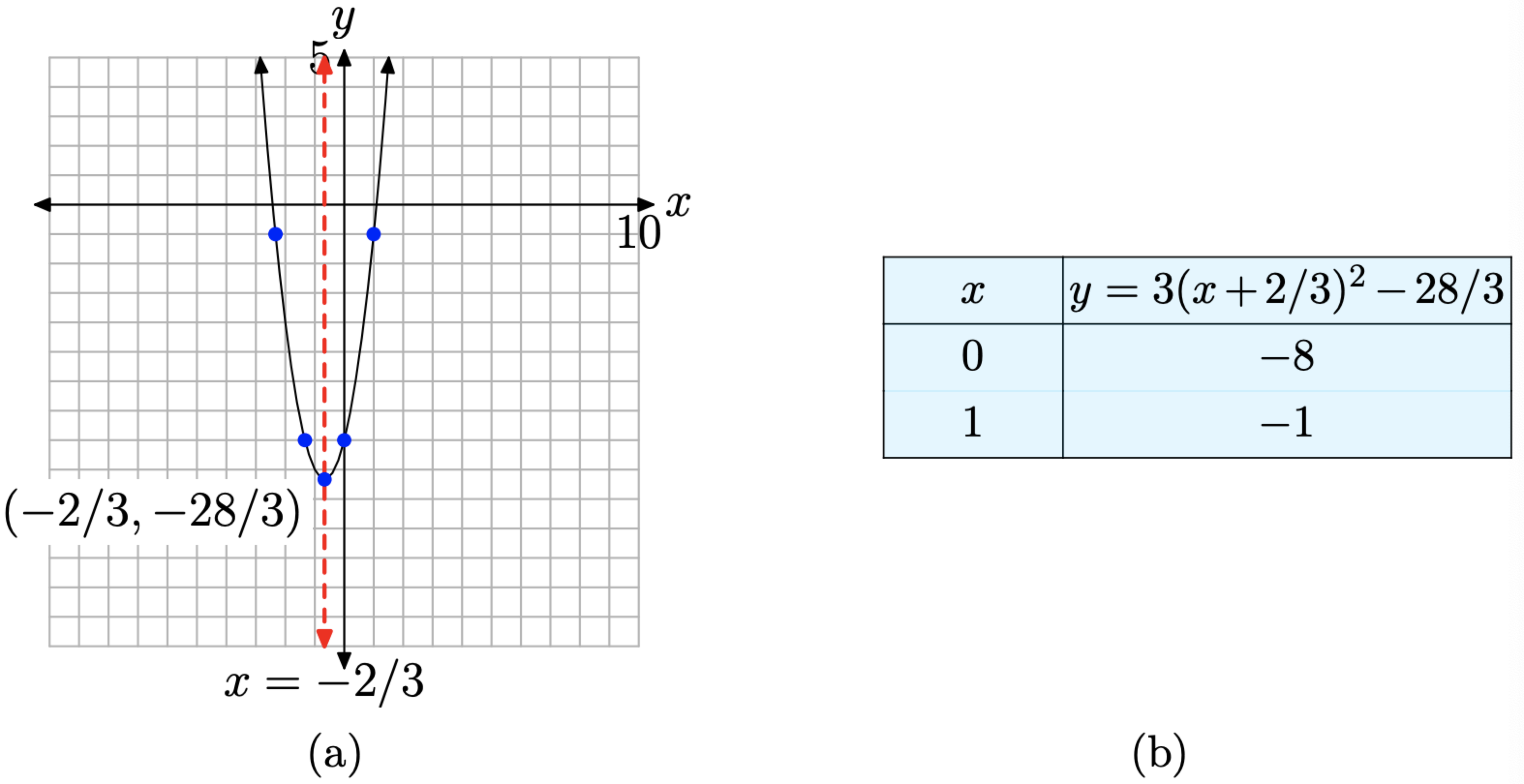
Complete the square to place \(f(x) = 3x^2 + 4x − 8\) in vertex form and sketch its graph.
Solution
Let’s begin again by factoring out the leading coefficient, in this case a 3.
\[f(x)=3\left[x^{2}+\frac{4}{3} x-\frac{8}{3}\right] \nonumber \]
Fractions add a degree of difficulty, but, if you follow the same routine as in the previous examples, you should be able to get the needed result. Take half of the coefficient of x and square the result; i.e., \([(1/2)(4/3)]^2 = [2/3]^2 = 4/9\).
Add and subtract this amount inside the parentheses so as to not change the equation.
\[f(x)=3\left[x^{2}+\frac{4}{3} x+\frac{4}{9}-\frac{4}{9}-\frac{8}{3}\right] \nonumber \]
Group the first three terms inside the parentheses. You’ll need a common denominator to combine constants.
\[f(x)=3\left[\left(x^{2}+\frac{4}{3} x+\frac{4}{9}\right)-\frac{4}{9}-\frac{24}{9}\right] \nonumber \]
The grouped terms inside the parentheses form a perfect square trinomial that is easily factored.
\[f(x)=3\left[\left(x+\frac{2}{3}\right)^{2}-\frac{28}{9}\right] \nonumber \]
Finally, redistribute the 3.
\[f(x)=3\left(x+\frac{2}{3}\right)^{2}-\frac{28}{3} \nonumber \]
This is a parabola that opens upward. It is also stretched by a factor of 3, so it will be narrower than all of our previous examples. The parabola is also shifted 2/3 units to the left, then 28/3 units downward, placing the vertex at (−2/3, −28/3), as shown in Figure \(\PageIndex{5}\)(a). The table in Figure \(\PageIndex{5}\)(b) calculates two points to the right of the axis of symmetry, and mirror points on the left of the axis of symmetry make for an accurate plot of the parabola.
Exercise
In Exercises 1-8, expand the binomial.
\((x+\frac{4}{5})^2\)
- Answer
-
\(x^2+\frac{8}{5}x+\frac{16}{25}\)
\((x−\frac{4}{5})^2\)
\((x+3)^2\)
- Answer
-
\(x^2+6x+9\)
\((x+5)^2\)
\((x−7)^2\)
- Answer
-
\(x^2−14x+49\)
\((x−\frac{2}{5})^2\)
\((x−6)^2\)
- Answer
-
\(x^2−12x+36\)
\((x−\frac{5}{2})^2\)
In Exercises 9-16, factor the perfect square trinomial.
\(x^2−\frac{6}{5}x+\frac{9}{25}\)
- Answer
-
\((x−\frac{3}{5})^2\)
\(x^2+5x+\frac{25}{4}\)
\(x^2−12x+36\)
- Answer
-
\((x−6)^2\)
\(x^2+3x+\frac{9}{4}\)
\(x^2+12x+36\)
- Answer
-
\((x+6)^2\)
\(x^2−\frac{3}{2}x+\frac{9}{16}\)
\(x^2+18x+81\)
- Answer
-
\((x+9)^2\)
\(x^2+10x+25\)
In Exercises 17-24, transform the given quadratic function into vertex form \(f(x) = (x−h)^2+k\) by completing the square.
\(f(x) = x^2−x+8\)
- Answer
-
\((x−\frac{1}{2})^2+\frac{31}{4}\)
\(f(x) = x^2+x−7\)
\(f(x) = x^2−5x−4\)
- Answer
-
\((x−\frac{5}{2})^2−\frac{41}{4}\)
\(f(x) = x^2+7x−1\)
\(f(x) = x^2+2x−6\)
- Answer
-
\((x+1)^2−7\)
\(f(x) = x^2+4x+8\)
\(f(x) = x^2−9x+3\)
- Answer
-
\((x−\frac{9}{2})−\frac{69}{4}\)
\(f(x) = x^2−7x+8\)
In Exercises 25-32, transform the given quadratic function into vertex form \(f(x) = a(x−h)^2+k\) by completing the square.
\(f(x) = −2x^2−9x−3\)
- Answer
-
\(−2(x+\frac{9}{4})^2+\frac{57}{8}\)
\(f(x) = −4x^2−6x+1\)
\(f(x) = 5x^2+5x+5\)
- Answer
-
\(5(x+\frac{1}{2})^2+\frac{15}{4}\)
\(f(x) = 3x^2−4x−6\)
\(f(x) = 5x^2+7x−3\)
- Answer
-
\(5(x+\frac{7}{10})^2−\frac{109}{20}\)
\(f(x) = 5x^2+6x+4\)
\(f(x) = −x^2−x+4\)
- Answer
-
\(−1(x+\frac{1}{2})^2+\frac{17}{4}\)
\(f(x) = −3x^2−6x+4\)
In Exercises 33-38, find the vertex of the graph of the given quadratic function.
\(f(x) = −2x^2+5x+3\)
- Answer
-
\((\frac{5}{4}, \frac{49}{8})\)
\(f(x) = x^2+5x+8\)
\(f(x) = −4x^2−4x+1\)
- Answer
-
\((−\frac{1}{2}, 2)\)
\(f(x) = 5x^2+7x+8\)
\(f(x) = 4x^2+2x+8\)
- Answer
-
\((−\frac{1}{4}, \frac{31}{4})\)
\(f(x) = x^2+x−7\)
In Exercises 39-44, find the axis of symmetry of the graph of the given quadratic function.
\(f(x) = −5x^2−7x−8\)
- Answer
-
\(x = −\frac{7}{10}\)
\(f(x) = x^2+6x+3\)
\(f(x) = −2x^2−5x−8\)
- Answer
-
\(x = −\frac{5}{4}\)
\(f(x) = −x^2−6x+2\)
\(f(x) = −5x^2+x+6\)
- Answer
-
\(x = \frac{1}{10}\)
\(f(x) = x^2−9x−6\)
For each of the quadratic functions in Exercises 45-66, perform each of the following tasks.
- Use the technique of completing the square to place the given quadratic function in vertex form.
- Set up a coordinate system on a sheet of graph paper. Label and scale each axis.
- Draw the axis of symmetry and label it with its equation. Plot the vertex and label it with its coordinates.
- Set up a table near your coordinate system that calculates the coordinates of two points on either side of the axis of symmetry. Plot these points and their mirror images across the axis of symmetry. Draw the parabola and label it with its equation
- Use the graph of the parabola to determine the domain and range of the quadratic function. Describe the domain and range using interval notation.
\(f(x) = x^2−8x+12\)
- Answer
-
\(f(x) = (x−4)^2−4\)
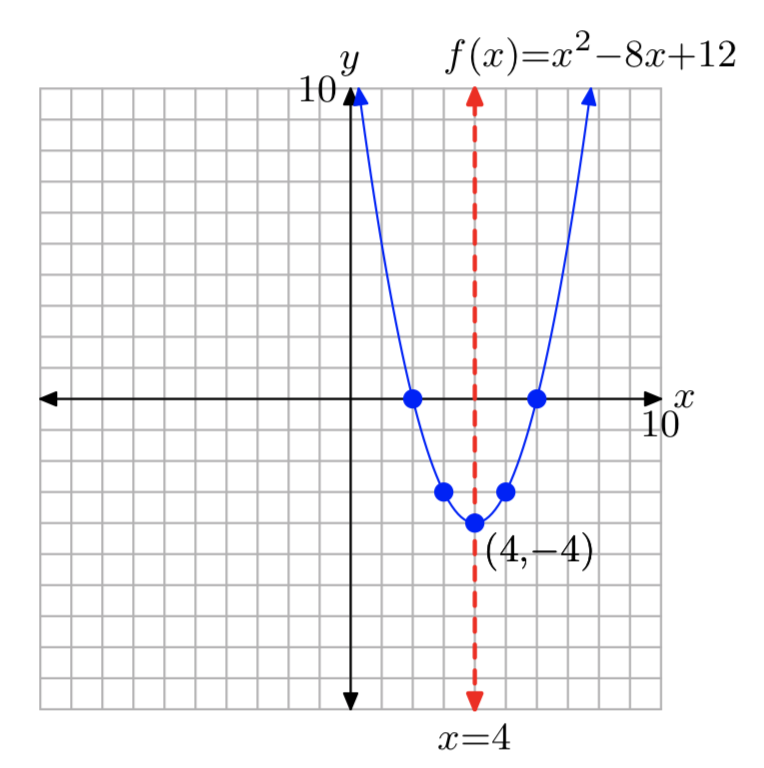
Domain = \(\mathbb{R}\), Range = [−4, \(\infty\))
\(f(x) = x^2+4x−1\)
\(f(x) = x^2+6x+3\)
- Answer
-
\(f(x) = (x+3)^2−6\)
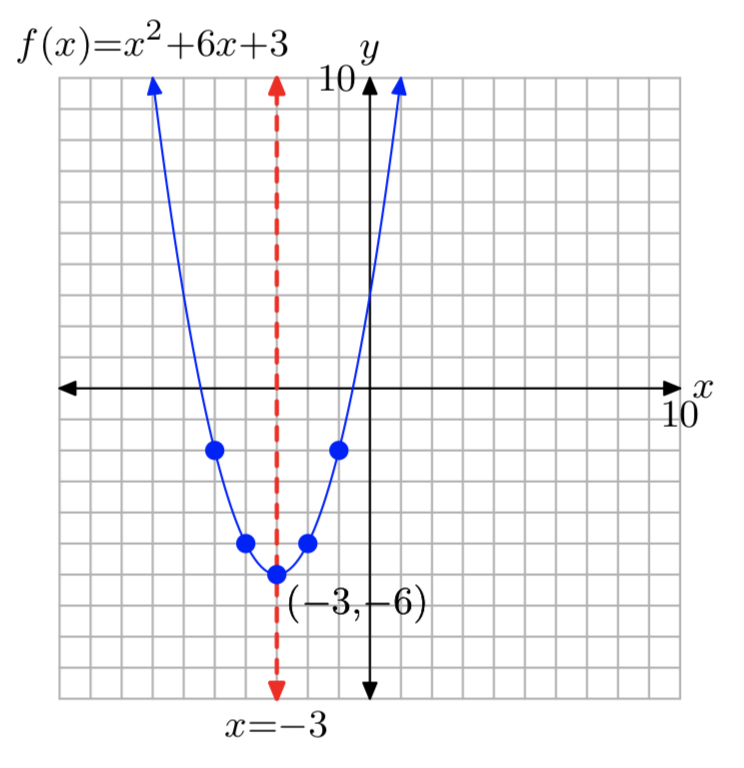
Domain = \(\mathbb{R}\), Range = [−6, \(\infty\))
\(f(x)=x^2−4x+1\)
\(f(x) = x^2−2x−6\)
- Answer
-
\(f(x) = (x−1)^2−7\)
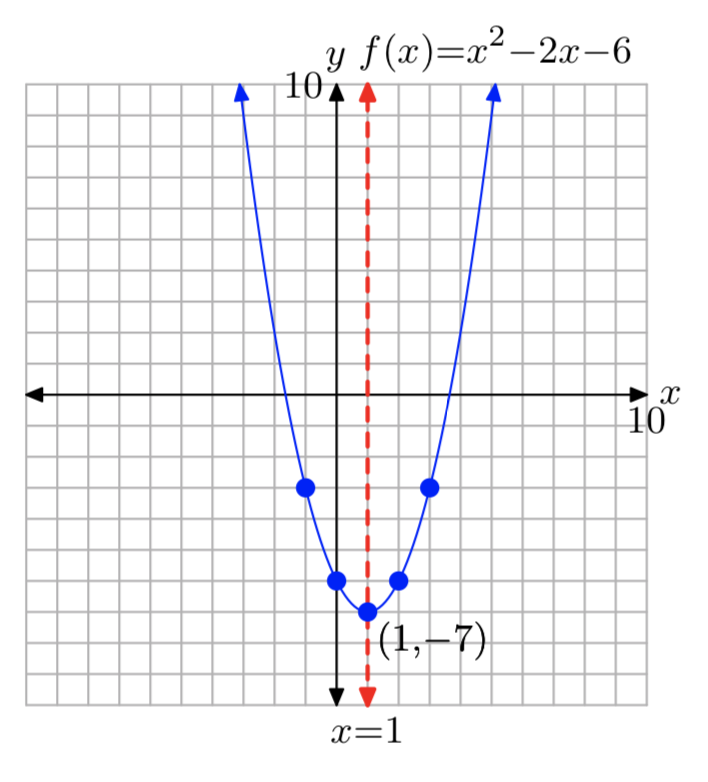
Domain = \(\mathbb{R}\), Range = [−7, \(\infty\))
\(f(x) = x^2+10x+23\)
\(f(x) = −x^2+6x−4\)
- Answer
-
\(f(x) = −(x−3)^2+5\)
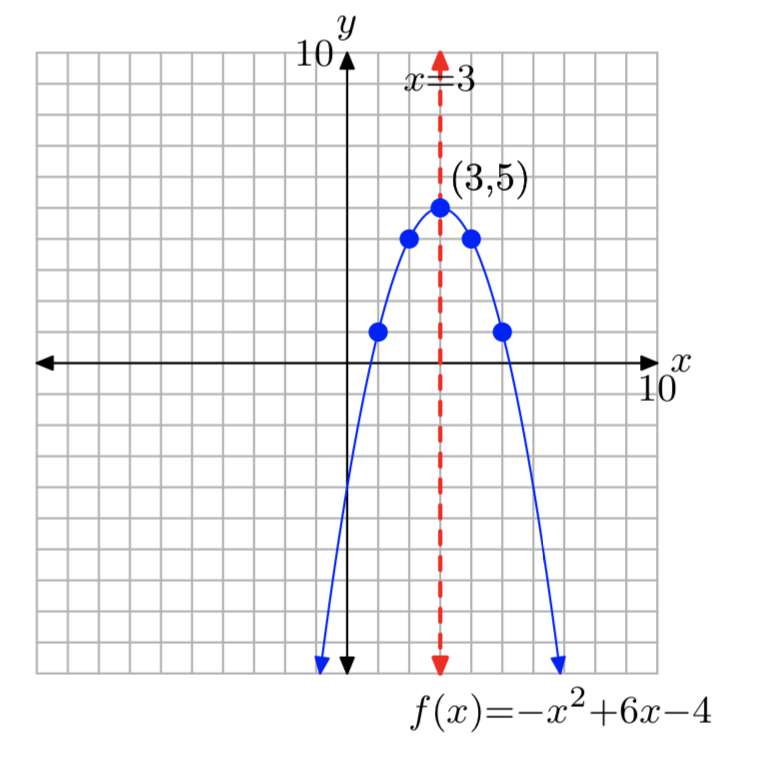
Domain = \(\mathbb{R}\), Range = (−\(\infty\), 5]
\(f(x) = −x^2−6x−3\)
\(f(x) = −x^2−10x−21\)
- Answer
-
\(f(x) = −(x+5)^2+4\)
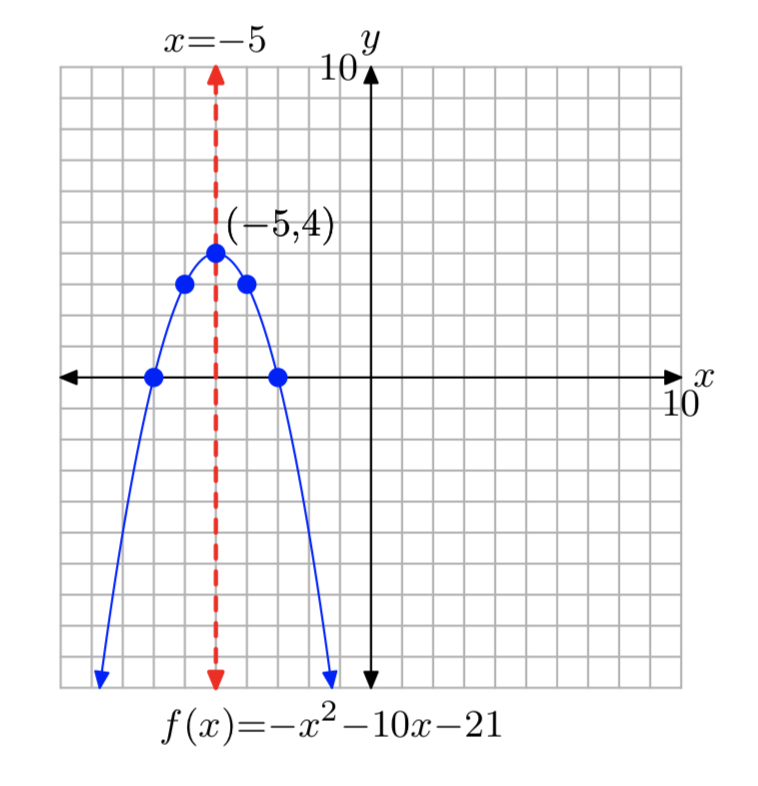
Domain = \(\mathbb{R}\), Range = (−\(\infty\), 4]
\(f(x) = −x^2+12x−33\)
\(f(x) = 2x^2−8x+3\)
- Answer
-
\(f(x) = 2(x−2)^2−5\)
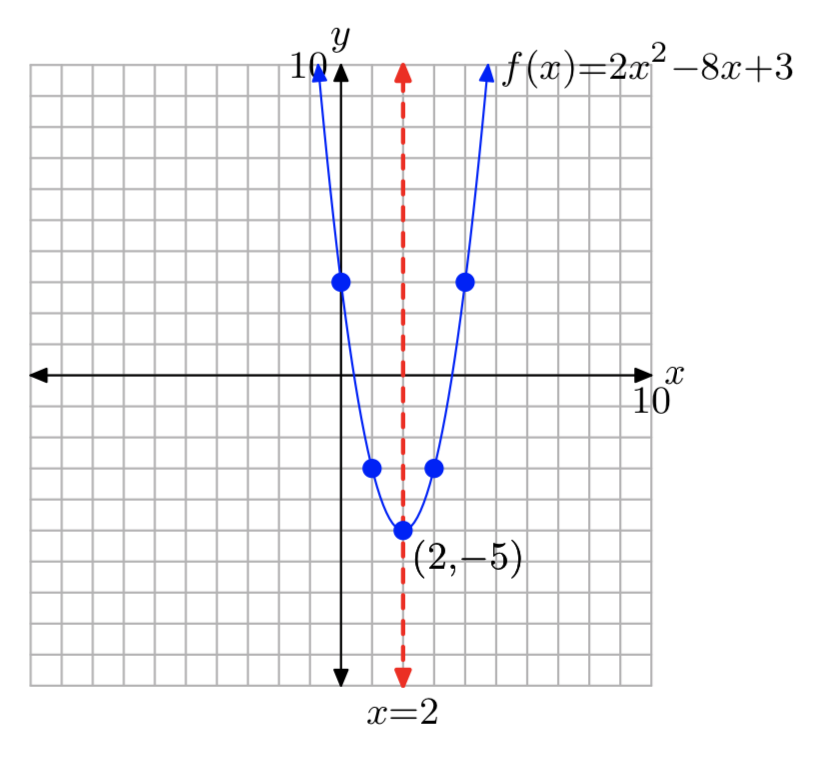
Domain = \(\mathbb{R}\), Range = [−5, \(\infty\))
\(f(x) = 2x^2+8x+4\)
\(f(x) = −2x^2−12x−13\)
- Answer
-
\(f(x) = −2(x+3)^2+5\)
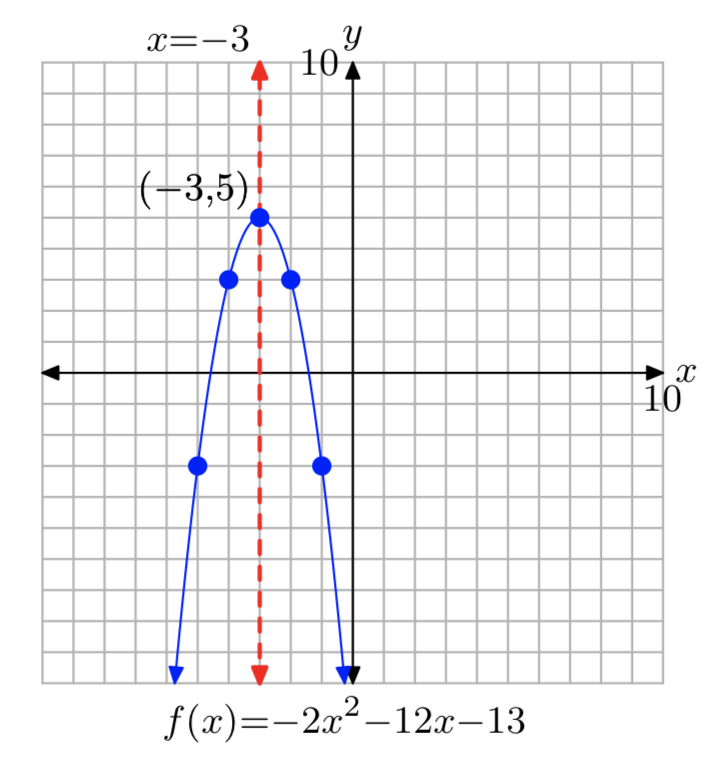
Domain = \(\mathbb{R}\), Range = (−\(\infty\), 5]
\(f(x) = −2x^2+24x−70\)
\(f(x) = \frac{1}{2}x^2−4x+5\)
- Answer
-
\(f(x) = \frac{1}{2}(x−4)^2−3\)
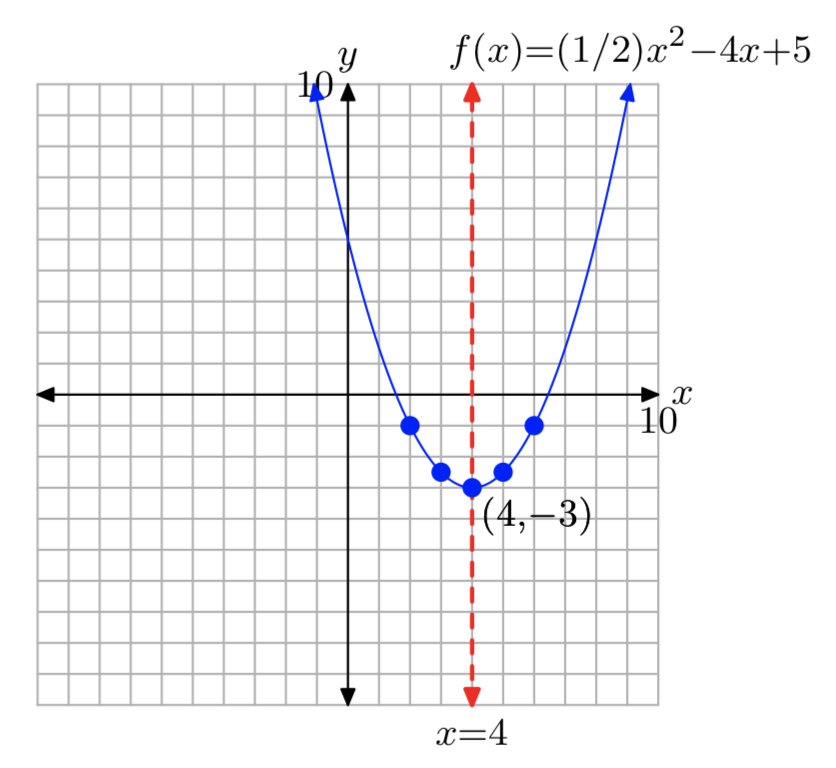
Domain = \(\mathbb{R}\), Range = [−3, \(\infty\))
\(f(x) = \frac{1}{2}x^2+4x+6\)
\(f(x) = −\frac{1}{2}x^2−3x+\frac{1}{2}\)
- Answer
-
\(f(x) = −\frac{1}{2}(x+3)^2+5\)
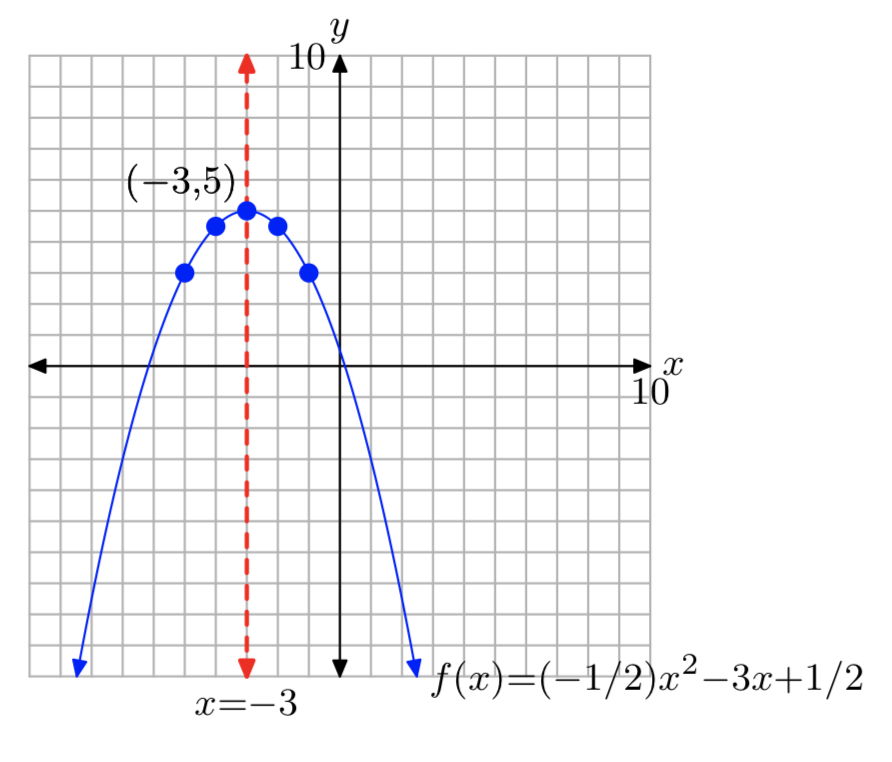
Domain = \(\mathbb{R}\), Range = (−\(\infty\), 5]
\(f(x) = −\frac{1}{2}x^2+4x−2\)
\(f(x) = 2x^2+7x−2\)
- Answer
-
\(f(x) = 2(x+\frac{7}{4})^2− \frac{65}{8}\)
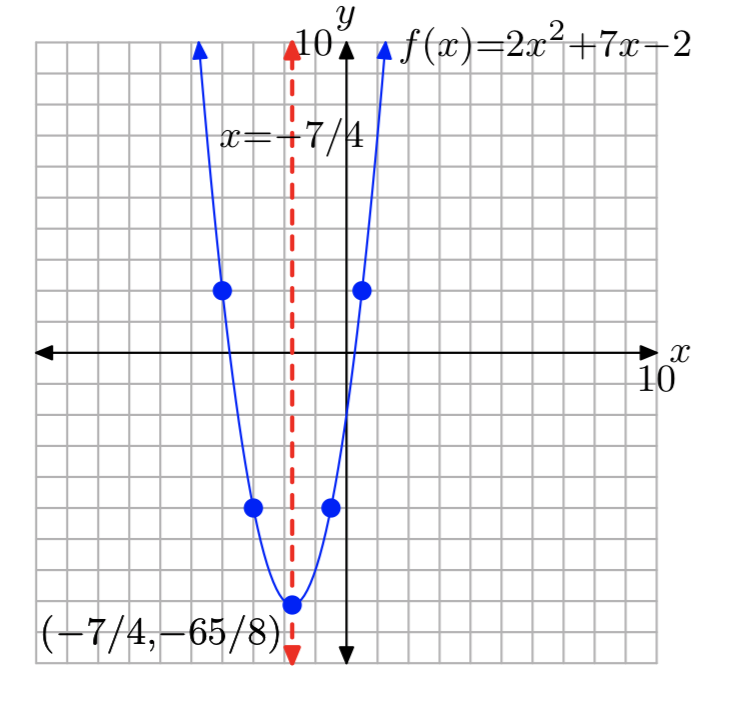
Domain = \(\mathbb{R}\), Range = [\(−\frac{65}{8}\), \(\infty\))
\(f(x) = −2x^2−5x−4\)
\(f(x) = −3x^2+8x−3\)
- Answer
-
\(f(x) = −3(x−\frac{4}{3})^2+\frac{7}{3}\)
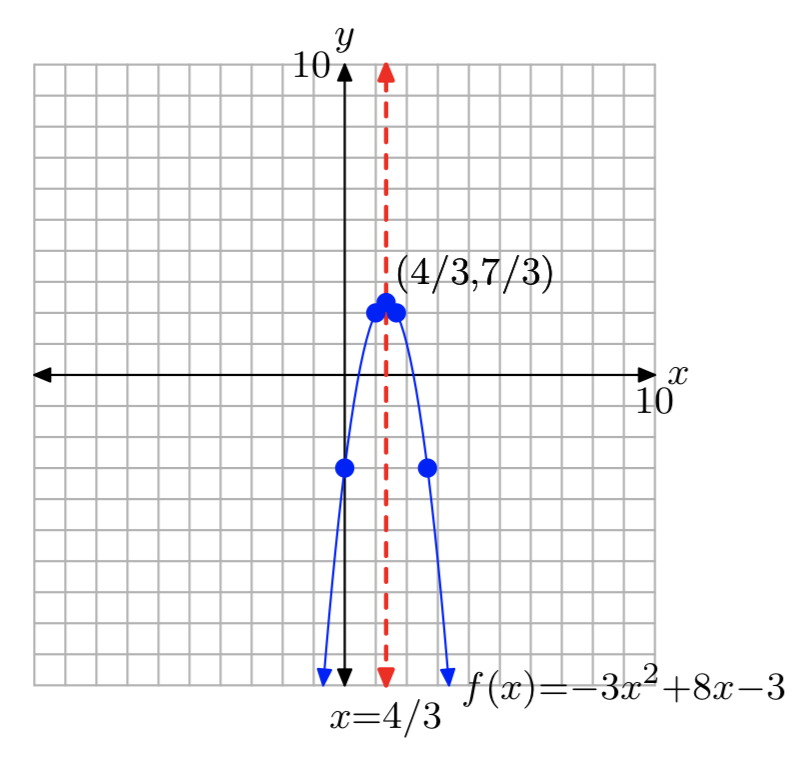
Domain = \(\mathbb{R}\), Range = (−\(\infty\), \(\frac{7}{3}\)]
\(f(x) = 3x^2+4x−6\)
In Exercises 67-72, find the range of the given quadratic function. Express your answer in both interval and set notation.
\(f(x) = −2x^2+4x+3\)
- Answer
-
(\(−\infty\), 5] = {x|\(x \le 5\)}
\(f(x) = x^2+4x+8\)
\(f(x) = 5x^2+4x+4\)
- Answer
-
[\(\frac{16}{5}\), \(\infty\)) = {x| \(x \ge 5\)}
\(f(x) = 3x^2−8x+3\)
\(f(x) = −x^2−2x−7\)
- Answer
-
(\(−\infty\),−6] = {x|\(x \le −6\)}
\(f(x) = x^2+x+9\)
Drill for Skill. In Exercises 73-76, evaluate the function at the given value b.
\(f(x) = 9x^2−9x+4\); b = −6
- Answer
-
382
\(f(x) = −12x^2+5x+2\); b = −3
\(f(x) = 4x^2−6x−4\); b = 11
- Answer
-
414
\(f(x) = −2x^2−11x−10\); b = −12
Drill for Skill. In Exercises 77-80, evaluate the function at the given expression.
Evaluate f(x+4) if \(f(x) = −5x^2+4x+2\).
- Answer
-
\(−5x^2−36x−62\)
Evaluate f(−4x−5) if \(f(x) = 4x^2+x+1\).
Evaluate f(4x−1) if \(f(x) = 4x^2+3x−3\).
- Answer
-
\(64x^2−20x−2\)
Evaluate f(−5x−3) if \(f(x) = −4x^2+x+4\).


