8.E: Quadratic Functions (Exercises)

Last updated
Save as PDF

Page ID: 19902

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

8.1: Introduction to Radical Notation

1) List all real square roots of $-400$.

Answer: There are no real square roots.

2) List all real square roots of $64$.

3) List all real square roots of $-25$.

Answer: There are no real square roots.

4) List all real square roots of $81$.

5) List all real square roots of $49$.

Answer: $-7,7$

6) List all real square roots of $-100$.

7) List all real square roots of $324$.

Answer: $-18,18$

8) List all real square roots of $36$.

9) List all real square roots of $-225$.

Answer: There are no real square roots.

10) List all real square roots of $0$.

11) List all real solutions of $x^2 = -225$.

Answer: There are no real solutions.

12) List all real solutions of $x^2 = -25$.

13) List all real solutions of $x^2 = 361$.

Answer: $-19,19$

14) List all real solutions of $x^2 = 256$.

15) List all real solutions of $x^2 = -400$.

Answer: There are no real solutions.

16) List all real solutions of $x^2 = 0$.

17) List all real solutions of $x^2 = 169$.

Answer: $-13,13$

18) List all real solutions of $x^{2}=-100$.

19) List all real solutions of $x^{2}=625$.

Answer: $-25,25$

20) List all real solutions of $x^{2}=324$.

In Exercises 21-30, simplify each of the given expressions.

21) $\sqrt{64}$

Answer: $8$

22) $-\sqrt{-529}$

23) $-\sqrt{-256}$

Answer: The expression is not a real number.

24) $\sqrt{-529}$

25) $-\sqrt{361}$

Answer: $-19$

26) $\sqrt{-361}$

27) $-\sqrt{100}$

Answer: $-10$

28) $-\sqrt{196}$

29) $\sqrt{441}$

Answer: $21$

30) $\sqrt{49}$

In Exercises 31-38, simplify each of the given expressions.

31) $(-\sqrt{17})^{2}$

Answer: $17$

32) $(-\sqrt{31})^{2}$

33) $(\sqrt{59})^{2}$

Answer: $59$

34) $(\sqrt{43})^{2}$

35) $(-\sqrt{29})^{2}$

Answer: $29$

36) $(-\sqrt{89})^{2}$

37) $(\sqrt{79})^{2}$

Answer: $79$

38) $(\sqrt{3})^{2}$

In Exercises 39-42, for each of the given equations, ﬁrst use the 5:intersect utility on the CALC menu of the graphing calculator to determine the solutions. Follow the Calculator Submission Guidelines, as demonstrated in Example 8.1.9 in reporting the solution on your homework paper. Second, solve the equation algebraically, then use your calculator to ﬁnd approximations of your answers and compare this second set with the ﬁrst set of answers.

39) $x^{2}=37$

Answer

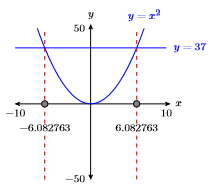
$Answer 8.1.39.png$

$\pm \sqrt{37} \approx \pm 6.082763$

40) $x^{2}=32$

41) $x^{2}=11$

Answer

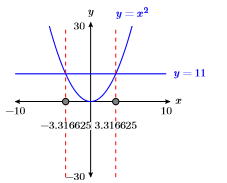
$Answer 8.1.41.png$

$\pm \sqrt{11} \approx \pm 3.316625$

42) $x^{2}=42$

8.2: Simplifying Radical Expressions

In Exercises 1-6, simplify the given expression, writing your answer using a single square root symbol. Check the result with your graphing calculator.

1) $\sqrt{5} \sqrt{13}$

Answer: $\sqrt{65}$

2) $\sqrt{2} \sqrt{7}$

3) $\sqrt{17} \sqrt{2}$

Answer: $\sqrt{34}$

4) $\sqrt{5} \sqrt{11}$

5) $\sqrt{5} \sqrt{17}$

Answer: $\sqrt{85}$

6) $\sqrt{17} \sqrt{3}$

In Exercises 7-26, convert each of the given expressions to simple radical form.

7) $\sqrt{56}$

Answer: $2 \sqrt{14}$

8) $\sqrt{45}$

9) $\sqrt{99}$

Answer: $3 \sqrt{11}$

10) $\sqrt{75}$

11) $\sqrt{150}$

Answer: $5 \sqrt{6}$

12) $\sqrt{90}$

13) $\sqrt{40}$

Answer: $2 \sqrt{10}$

14) $\sqrt{171}$

15) $\sqrt{28}$

Answer: $2 \sqrt{7}$

16) $\sqrt{175}$

17) $\sqrt{153}$

Answer: $3 \sqrt{17}$

18) $\sqrt{125}$

19) $\sqrt{50}$

Answer: $5 \sqrt{2}$

20) $\sqrt{88}$

21) $\sqrt{18}$

Answer: $3 \sqrt{2}$

22) $\sqrt{117}$

23) $\sqrt{44}$

Answer: $2 \sqrt{11}$

24) $\sqrt{20}$

25) $\sqrt{104}$

Answer: $2 \sqrt{26}$

26) $\sqrt{27}$

In Exercises 27-34, ﬁnd the length of the missing side of the right triangle. Your ﬁnal answer must be in simple radical form.

27)

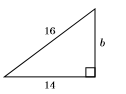
Answer: $2 \sqrt{15}$

28)

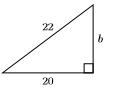
29)

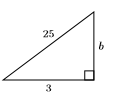
Answer: $2 \sqrt{154}$

30)

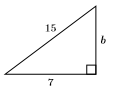
31)

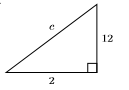
Answer: $2 \sqrt{37}$

32)

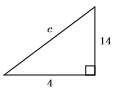
33)

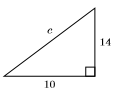
Answer: $2 \sqrt{74}$

34)

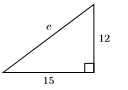
35) In the ﬁgure below, a right triangle is inscribed in a semicircle. What is the area of the shaded region?

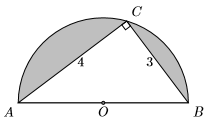
Answer: $\dfrac{25}{8} \pi-6$

36) In the ﬁgure below, a right triangle is inscribed in a semicircle. What is the area of the shaded region?

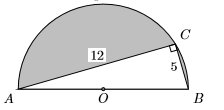
37) The longest leg of a right triangle is $10$ feet longer than twice the length of its shorter leg. The hypotenuse is $4$ feet longer than three times the length of the shorter leg. Find the lengths of all three sides of the right triangle.

Answer: $7,24,25$

38) The longest leg of a right triangle is $2$ feet longer than twice the length of its shorter leg. The hypotenuse is $3$ feet longer than twice the length of the shorter leg. Find the lengths of all three sides of the right triangle.

39) A ladder $19$ feet long leans against the garage wall. If the base of the ladder is $5$ feet from the garage wall, how high up the garage wall does the ladder reach? Use your calculator to round your answer to the nearest tenth of a foot.

Answer: $18.3$ feet

40) A ladder $19$ feet long leans against the garage wall. If the base of the ladder is $6$ feet from the garage wall, how high up the garage wall does the ladder reach? Use your calculator to round your answer to the nearest tenth of a foot.

8.3: Completing the Square

In Exercises 1-8, ﬁnd all real solutions of the given equation. Place your ﬁnal answers in simple radical form.

1) $x^{2}=84$

Answer: $\pm 2 \sqrt{21}$

2) $x^{2}=88$

3) $x^{2}=68$

Answer: $\pm 2 \sqrt{17}$

4) $x^{2}=112$

5) $x^{2}=-16$

Answer: No real solutions

6) $x^{2}=-104$

7) $x^{2}=124$

Answer: $\pm 2 \sqrt{31}$

8) $x^{2}=148$

In Exercises 9-12, ﬁnd all real solutions of the given equation. Place your ﬁnal answers in simple radical form.

9) $(x+19)^{2}=36$

Answer: $-25,-13$

10) $(x-4)^{2}=400$

11) $(x+14)^{2}=100$

Answer: $-24,-4$

12) $(x-15)^{2}=100$

In Exercises 13-18, square each of the following binomials.

13) $(x+23)^{2}$

Answer: $x^{2}+46 x+529$

14) $(x-5)^{2}$

15) $(x+11)^{2}$

Answer: $x^{2}+22 x+121$

16) $(x-7)^{2}$

17) $(x-25)^{2}$

Answer: $x^{2}-50 x+625$

18) $(x+4)^{2}$

In Exercises 19-24, factor each of the following trinomials.

19) $x^{2}+24 x+144$

Answer:: $(x+12)^{2}$

20) $x^{2}-16 x+64$

21) $x^{2}-34 x+289$

Answer:: $(x-17)^{2}$

22) $x^{2}+8 x+16$

23) $x^{2}-20 x+100$

Answer:: $(x-10)^{2}$

24) $x^{2}+16 x+64$

In Exercises 25-36, for each expression, complete the square to form a perfect square trinomial. Check your answer by factoring your result. Be sure to check your middle term.

25) $x^{2}-20 x$

Answer: $x^{2}-20 x+100$

26) $x^{2}-10 x$

27) $x^{2}-6 x$

Answer: $x^{2}-6 x+9$

28) $x^{2}-40 x$

29) $x^{2}+20 x$

Answer: $x^{2}+20 x+100$

30) $x^{2}+26 x$

31) $x^{2}+7 x$

Answer: $x^{2}+7 x+\frac {49}{4}$

32) $x^{2}+19 x$

33) $x^{2}+15 x$

Answer: $x^{2}+15 x+\frac {225}{4}$

34) $x^{2}+25 x$

35) $x^{2}-5 x$

Answer: $x^{2}-5 x+\frac {25}{4}$

36) $x^{2}-3 x$

In Exercises 37-52, ﬁnd all real solutions, if any, of the given equation. Place your ﬁnal answers in simple radical form.

37) $x^{2}=18 x-18$

Answer: $9-3 \sqrt{7}, 9+3 \sqrt{7}$

38) $x^{2}=12 x-18$

39) $x^{2}=16 x-16$

Answer: $8-4 \sqrt{3}, 8+4 \sqrt{3}$

40) $x^{2}=12 x-4$

41) $x^{2}=-16 x-4$

Answer: $-8-2 \sqrt{15},-8+2 \sqrt{15}$

42) $x^{2}=-12 x-12$

43) $x^{2}=18 x-9$

Answer: $9-6 \sqrt{2}, 9+6 \sqrt{2}$

44) $x^{2}=16 x-10$

45) $x^{2}=16 x-8$

Answer: $8-2 \sqrt{14}, 8+2 \sqrt{14}$

46) $x^{2}=10 x-5$

47) $x^{2}=-18 x-18$

Answer: $-9-3 \sqrt{7},-9+3 \sqrt{7}$

48) $x^{2}=-10 x-17$

49) $x^{2}=-16 x-20$

Answer: $-8-2 \sqrt{11},-8+2 \sqrt{11}$

50) $x^{2}=-16 x-12$

51) $x^{2}=-18 x-1$

Answer: $-9-4 \sqrt{5},-9+4 \sqrt{5}$

52) $x^{2}=-12 x-8$

In Exercises 53-56, solve the given equation algebraically, stating your ﬁnal answers in simple radical form. Next, use the graphing calculator to solve the equation, following the technique outlined in Example 8.3.8. Use the Calculator Submission Guidelines, as demonstrated inExample 8, when reporting the solution on your homework. Compare the solutions determined by the two methods.

53) $x^{2}-2 x-17=0$

Answer: $1-3 \sqrt{2}, 1+3 \sqrt{2}$

54) $x^{2}-4 x-14=0$

55) $x^{2}-6 x-3=0$

Answer: $3-2 \sqrt{3}, 3+2 \sqrt{3}$

56) $x^{2}-4 x-16=0$

8.4: The Quadratic Formula

In Exercises 1-8, solve the given equation by factoring the trinomial using the $ac$-method, then applying the zero product property. Secondly, craft a second solution using the quadratic formula. Compare your answers.

1) $x^{2}-3 x-28=0$

Answer: $-4,7$

2) $x^{2}-4 x-12=0$

3) $x^{2}-8 x+15=0$

Answer: $3,5$

4) $x^{2}-6 x+8=0$

5) $x^{2}-2 x-48=0$

Answer: $-6,8$

6) $x^{2}+9 x+8=0$

7) $x^{2}+x-30=0$

Answer: $-6,5$

8) $x^{2}-17 x+72=0$

In Exercises 9-16, use the quadratic formula to solve the given equation. Your ﬁnal answers must be reduced to lowest terms and all radical expressions must be in simple radical form.

9) $x^{2}-7 x-5=0$

Answer: $\dfrac{7 \pm \sqrt{69}}{2}$

10) $3 x^{2}-3 x-4=0$

11) $2 x^{2}+x-4=0$

Answer: $\dfrac{-1 \pm \sqrt{33}}{4}$

12) $2 x^{2}+7 x-3=0$

13) $x^{2}-7 x-4=0$

Answer: $\dfrac{7 \pm \sqrt{65}}{2}$

14) $x^{2}-5 x+1=0$

15) $4 x^{2}-x-2=0$

Answer: $\dfrac{1 \pm \sqrt{33}}{8}$

16) $5 x^{2}+x-2=0$

In Exercises 17-24, use the quadratic formula to solve the given equation. Your ﬁnal answers must be reduced to lowest terms and all radical expressions must be in simple radical form.

17) $x^{2}-x-11=0$

Answer: $\dfrac{1 \pm 3 \sqrt{5}}{2}$

18) $x^{2}-11 x+19=0$

19) $x^{2}-9 x+9=0$

Answer: $\dfrac{9 \pm 3 \sqrt{5}}{2}$

20) $x^{2}+5 x-5=0$

21) $x^{2}-3 x-9=0$

Answer: $\dfrac{3 \pm 3 \sqrt{5}}{2}$

22) $x^{2}-5 x-5=0$

23) $x^{2}-7 x-19=0$

Answer: $\dfrac{7 \pm 5 \sqrt{5}}{2}$

24) $x^{2}+13 x+4=0$

In Exercises 25-32, use the quadratic formula to solve the given equation. Your ﬁnal answers must be reduced to lowest terms and all radical expressions must be in simple radical form.

25) $12 x^{2}+10 x-1=0$

Answer: $\dfrac{-5 \pm \sqrt{37}}{12}$

26) $7 x^{2}+6 x-3=0$

27) $7 x^{2}-10 x+1=0$

Answer: $\dfrac{5 \pm 3 \sqrt{2}}{7}$

28) $7 x^{2}+4 x-1=0$

29) $2 x^{2}-12 x+3=0$

Answer: $\dfrac{6 \pm \sqrt{30}}{2}$

30) $2 x^{2}-6 x-13=0$

31) $13 x^{2}-2 x-2=0$

Answer: $\dfrac{1 \pm 3 \sqrt{3}}{13}$

32) $9 x^{2}-2 x-3=0$

33) An object is launched vertically and its height $y$ (in feet) above ground level is given by the equation $y = 240 + 160t− 16t^2$, where $t$ is the time (in seconds) that has passed since its launch. How much time must pass after the launch before the object returns to ground level? After placing the answer in simple form and reducing, use your calculator to round the answer to the nearest tenth of a second.

Answer: $11.3$ seconds

34) An object is launched vertically and its height $y$ (in feet) above ground level is given by the equation $y = 192 + 288t− 16t^2$, where $t$ is the time (in seconds) that has passed since its launch. How much time must pass after the launch before the object returns to ground level? After placing the answer in simple form and reducing, use your calculator to round the answer to the nearest tenth of a second.

35) A manufacturer’s revenue $R$ accrued from selling $x$ widgets is given by the equation $R = 6000x − 5x^2$. The manufacturer’s costs for building $x$ widgets is given by the equation $C = 500000 + 5.25x$. The break even point for the manufacturer is deﬁned as the number of widgets built and sold so the the manufacturer’s revenue and costs are identical. Find the number of widgets required to be built and sold so that the manufacturer “breaks even.” Round your answers to the nearest widget.

Answer: $90$ widgets, $1109$ widgets

36) A manufacturer’s revenue $R$ accrued from selling $x$ widgets is given by the equation $R = 4500x−15.25x^2$. How many widgets must be sold so that the manufacturer’s revenue is $\$125,000$? Round your answers to the nearest widget.

37) Mike gets on his bike at noon and begins to ride due north at a constant rate of $6$ miles per hour. At 2:00 pm, Todd gets on his bike at the same starting point and begins to ride due east at a constant rate of $8$ miles per hour. At what time of the day will they be $60$ miles apart (as the crow ﬂies)? Don’t worry about simple form, just report the time of day, correct to the nearest minute.

Answer: 7:12 pm

38) Mikaela gets on her bike at noon and begins to ride due north at a constant rate of $4$ miles per hour. At 1:00 pm, Rosemarie gets on her bike at the same starting point and begins to ride due east at a constant rate of $6$ miles per hour. At what time of the day will they be $20$ miles apart (as the crow ﬂies)? Don’t worry about simple form, just report the time of day, correct to the nearest minute.

39) The area of a rectangular ﬁeld is $76$ square feet. The length of the ﬁeld is $7$ feet longer than its width. Find the dimensions of the ﬁeld, correct to the nearest tenth of a foot.

Answer: $5.9$ by $12.9$ feet

40) The area of a rectangular ﬁeld is $50$ square feet. The length of the ﬁeld is $8$ feet longer than its width. Find the dimensions of the ﬁeld, correct to the nearest tenth of a foot.

41) Mean concentrations of carbon dioxide over Mauna Loa, Hawaii, are gathered by the Earth System Research Laboratory (ESRL) in conjunction with the National Oceanic and Atmosphere Administration (NOAA). Mean annual concentrations in parts per million for the years 1962, 1982, and 2002 are shown in the following table.

Year	1962	1982	2002
Concentration (ppm)	318	341	373

A quadratic model is ﬁtted to this data, yielding \[C =0 .01125t^2 +0 .925t+ 318 \nonumber \] where $t$ is the number of years since 1962 and $C$ is the mean annual concentration (in parts per million) of carbon dioxide over Mauna Loa. Use the model to ﬁnd the year when the mean concentration of carbon dioxide was $330$ parts per million. Round your answer to the nearest year.

Answer: 1973

42) The U.S. Census Bureau provides historical data on the number of Americans over the age of $85$.

Year	1970	1990	2010
Population over 85 (millions)	1.4	3.0	5.7

A quadratic model is ﬁtted to this data, yielding \[P =0 .01375t^2 +0 .0525t+1 .4 \nonumber \] where $t$ is the number of years since 1970 and $P$ is number of Americans (in millions) over the age of $85$. Use the model to ﬁnd the year when the number of Americans over the age of $85$ was $2,200,000$. Round your answer to the nearest year.

Search

Text Color

Text Size

Margin Size

Font Type