8.1: Introduction to Radical Notation
- Page ID
- 19898
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We know how to square a number. For example:
- \(5^2 = 25\)
- \((−5)^2 = 25\)
Taking the square root of a number is the opposite of squaring.
- The nonnegative square root of \(25\) is \(5\).
- The negative square root of \(25\) is \(−5\).
Thus, when searching for a square root of a number, we are searching for number whose square is equal to our number.
Example \(\PageIndex{1}\)
Find the square roots of \(81\).
Solution
We are looking for a number whose square is \(81\).
- Because \(9^2 = 81\), the nonnegative square root of \(81\) is \(9\).
- Because \((−9)^2 = 81\), the negative square root of \(81\) is \(−9\).
Hence, \(81\) has two square roots, \(−9\) and \(9\).
Exercise \(\PageIndex{1}\)
Find the square roots of \(64\).
- Answer
-
\(8\) and \(−8\)
Example \(\PageIndex{2}\)
Find the square roots of \(0\).
Solution
We are looking for a number whose square is \(0\).
- Because \(0^2 = 0\), the nonnegative square root of \(0\) is \(0\).
No other number squared will equal zero. Hence, zero has exactly one square root, namely zero.
Exercise \(\PageIndex{2}\)
Find the square roots of \(100\).
- Answer
-
\(10\) and \(−10\)
Example \(\PageIndex{3}\)
Find the square roots of \(−36\).
Solution
We are looking for a number whose square is \(−36\). However, every time you square a real number, the result is never negative. Hence, \(−36\) has no real square roots.1
Exercise \(\PageIndex{3}\)
Find the square roots of \(−25\).
- Answer
-
no real square roots
The introductions in Examples \(\PageIndex{1}\), \(\PageIndex{2}\), and \(\PageIndex{3}\) lead to the following definition.
Defining the Square Roots of a Number
The solutions of \(x^2 = a\) are called square roots of \(a\).
Case: \(a>0\). The equation \(x^2 = a\) has two real solutions, namely \(x =\pm \sqrt{a}\).
- The notation\(\sqrt{a}\) calls for the nonegative square root.
- The notation \(−\sqrt{a}\) calls for the negative square root.
Case: \(a = 0\). The equation \(x^2 = 0\) has exactly one solution, namely \(x = 0\).
Case: \(a<0\). The equation \(x^2 = a\) has no real solutions.
Example \(\PageIndex{4}\)
Solve \(x^2 = 9\) for \(x\), then simplify your answers.
Solution
Because the right-hand side of \(x^2 = 9\) is positive, the equation has two solutions.
\[\begin{align*} x^2 &= 9 \quad \color {Red} \text {Original equation.}\\ x &= \pm \sqrt{9} \quad \color {Red} \text {Two answers: } -\sqrt{9} \text { and } \sqrt{9} \end{align*} \nonumber\]
To simplify these answers, we need to understand the following facts:
- \(\sqrt{9}\) calls for the nonnegative square root of \(9\). Because \((3)^2 = 9\), the nonnegative square root of \(9\) is \(3\). Hence, \(\sqrt{9} = 3\).
- \(-\sqrt{9}\) calls for the negative square root of \(9\). Because \((−3)^2 = 9\), the negative square root of \(9\) is \(−3\). Hence, \(-\sqrt{9}=−3\).
Thus, the solutions of \(x^2 = 9\) are \(x = \pm 3\), which is equivalent to saying “\(x =−3\) or \(x = 3\).”
Exercise \(\PageIndex{4}\)
Solve \(x^2 = 16\) for \(x\), then simplify your answers.
- Answer
-
\(4\), \(-4\)
Example \(\PageIndex{5}\)
Solve \(x^2 = 0\) for \(x\), then simplify the answer.
Solution
There is only one number whose square equals \(0\), namely \(0\).
\[\begin{align*} x^2 &= 0 \quad \color {Red} \text {Original equation.}\\ x &= 0 \quad \color {Red} \text {One answer: } (0)^2 = 0. \end{align*} \nonumber\]
Thus, the only solution of \(x^2 = 0\) is \(x = 0\). Consequently, the nonnegative square root of zero is zero. Hence, \(\sqrt{0} = 0\).
Exercise \(\PageIndex{5}\)
Solve \(x^2 = 49\) for \(x\), then simplify the answers.
- Answer
-
\(7\), \(-7\)
Example \(\PageIndex{6}\)
Solve \(x^2 =−4\) for \(x\), then simplify the answer.
Solution
You cannot square a real number and get a negative result. Hence, \(x^2 = −4\) has no real solutions. Therefore, \(\sqrt{-4}\) is not a real number.
Exercise \(\PageIndex{6}\)
Solve \(x^2 = −9\) for \(x\), then simplify the answers.
- Answer
-
no real solutions
Example \(\PageIndex{7}\)
Simplify each of the following:
- \(\sqrt{121}\)
- -\(\sqrt{225}\)
- \(\sqrt{-100}\)
- -\(\sqrt{324}\)
Solution
Remember, the notation \(\sqrt{a}\) calls for the nonnegative square root of \(a\), while the notation -\(\sqrt{a}\) calls for the negative square root of \(a\).
- Because \(11^2 = 121\), the nonnegative square root of \(225\) is \(-15\). Thus:\[-\sqrt{225} = -15 \nonumber \]
- Because \((-15)^2 = 225\), the nonnegative square root of \(121\) is \(11\). Thus:\[\sqrt{121} = 11 \nonumber \]
- You cannot square a real number and get \(−100\). Therefore, \(\sqrt{-100}\) is not a real number.
- Because \((-18)^2 = 324\), the nonnegative square root of \(324\) is \(-18\). Thus:\[-\sqrt{324} = -18 \nonumber \]
Exercise \(\PageIndex{7}\)
Simplify: \(−\sqrt{144}\)
- Answer
-
\(-12\)
Squaring “undoes” taking the square root.
Squaring square roots
If \(a>0\), then both \(-\sqrt{a}\) and \(\sqrt{a}\) are solutions of \(x^2 = a\). Consequently, if we substitute each of them into the equation \(x^2 = a\), we get:
\((-\sqrt{a})^2 = a\) and \((\sqrt{a})^2 = a\)
Example \(\PageIndex{8}\)
Simplify each of the following expressions:
- \((\sqrt{5})^2\)
- \((-\sqrt{7})^2\)
- \((\sqrt{-11})^2\)
Solution
We’ll handle each case carefully.
- Because \(\sqrt{5}\) is a solution of \(x^2 = 5\), if we square \(\sqrt{5}\), we should get \(5\).\[(\sqrt{5})^2 =5 \nonumber \]
- Because \(-\sqrt{7}\) is a solution of \(x^2 = 7\), if we square \(-\sqrt{7}\), we should get \(7\).\[(-\sqrt{7})^2 =7 \nonumber \]
- Because \(x^2 = −11\) has no real answers, \(\sqrt{-11}\) is not a real number. Advanced courses such as college algebra or trigonometry will introduce the complex number system and show how to handle this expression.
Exercise \(\PageIndex{8}\)
Simplify: \((−\sqrt{21})^2\)
- Answer
-
\(21\)
Using the Graphing Calculator
Up to this point, the equation \(x^2 = a\) has involved perfect squares. For example, if we start with \(x^2 = 25\), then the solutions are \(x = \pm \sqrt {25}\). Because \(25\) is a perfect square, we can simplify further, arriving at \(x =\pm 5\).
However, the right-hand side of \(x^2 = a\) does not have to be a perfect square. For example, the equation \(x^2 = 7\) has two real solutions, \(x =\pm \sqrt {7}\). Because \(7\) is not a perfect square, we cannot simplify further. In the next example, we’ll use the graphing calculator to compare this algebraic solution with a graphical solution and hopefully provide some assurance that \(−\sqrt{7}\) and \(\sqrt {7}\) are perfectly valid solutions of \(x^2 = 7\).
Example \(\PageIndex{9}\)
Use the graphing calculator to solve \(x^2 = 7\). Then solve the equation algebraically and compare answers.
Solution
Enter each side of the equation \(x^2 = 7\) in the Y= menu (see Figure \(\PageIndex{1}\)), then select 6:ZStandard to produce the image in Figure \(\PageIndex{1}\).
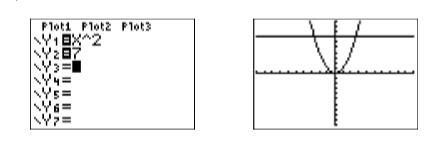
Use the 5:intersect utility on the CALC menu to find the points of intersection. Press ENTER in response to “First curve,” press ENTER in response to “Second curve,” then use the arrow keys to move the cursor closer to the point of intersection on the left than the one on the right. Press ENTER in response to “Guess.” This will produce the point of intersection shown in image on the left in Figure \(\PageIndex{2}\). Repeat the procedure to find the point of intersection in the image on the right in Figure \(\PageIndex{2}\).
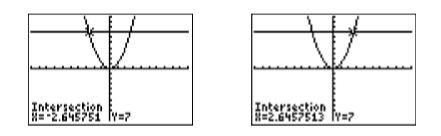
The approximate solutions of \(x^2 = 7\) are \(x≈− 2.645751\) and \(x ≈2.6457513\).
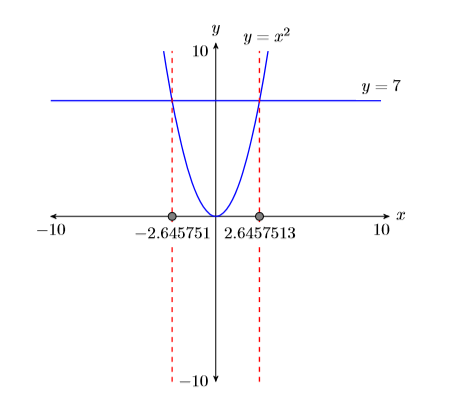
Reporting the solution on your homework: Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{3}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{3}\)).
- Label each graph with its equation (see Figure \(\PageIndex{3}\)).
- Drop dashed vertical lines through each point of intersection. Shade and label the x-values of the points where the dashed vertical line crosses the x-axis. These are the solutions of the equation \(x^2 = 7\) (see Figure \(\PageIndex{3}\)).
Now we solve the equation algebraically.
\[\begin{align*} x^2 &= 7 \\ x &= \pm \sqrt{7} \end{align*} \nonumber\]
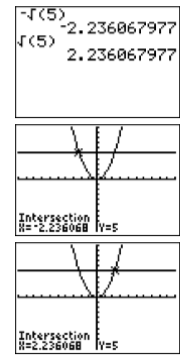
At this point, the question is: “Do these algebraic solutions match the graphical solutions in Figure \(\PageIndex{3}\)?” Let’s use our calculator to compare results. Locate the square root symbol \(\sqrt{ }\) on the calculator case above the \(x^2\) key in the leftmost column on the calculator keyboard. Note that we will have to use the \(2^{nd}\) key to access this operator. Enter \(-\sqrt{(7)}\) and press ENTER. Then enter \(\sqrt{(7)}\) and press ENTER. The results are shown in Figure \(\PageIndex{4}\).
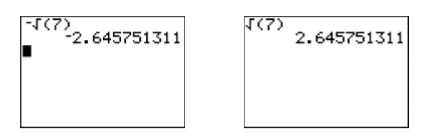
Thus, \(-\sqrt{7} ≈− 2.645751311\) and \(\sqrt{7} ≈ 2.645751311\). Note how these closely match the graphical approximations in Figure \(\PageIndex{3}\).
Exercise \(\PageIndex{9}\)
Solve the equation \(x^2 =5\) both algebraically and graphically, then compare your answers.
- Answer
-
\(-\sqrt{5}\), \(\sqrt{5}\)
Example \(\PageIndex{10}\)
Use the graphing calculator to solve \(x^2 = −5\). Then solve the equation algebraically and compare answers.
Solution
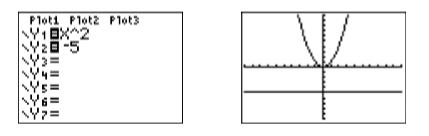
Enter each side of the equation \(x^2 = −5\) in the Y= menu (see Figure \(\PageIndex{5}\)), then select 6:ZStandard to produce the image in Figure \(\PageIndex{5}\).
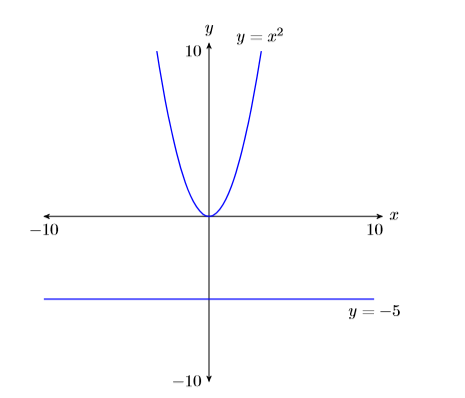
Reporting the solution on your homework: Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.
- Label the horizontal and vertical axes with \(x\) and \(y\), respectively (see Figure \(\PageIndex{6}\)).
- Place your WINDOW parameters at the end of each axis (see Figure \(\PageIndex{6}\)).
- Label each graph with its equation (see Figure \(\PageIndex{6}\)).
Because there are no points of intersection, the graph in Figure \(\PageIndex{6}\) informs us that the equation \(x^2 = −5\) has no real solutions. Now we solve the equation algebraically. \(x^2 = −5\) However, you cannot square a real number and get a negative answer. Hence, the equation \(x^2 = −5\) has no real solutions. This agrees completely with the graph in Figure \(\PageIndex{6}\).
Approximating Square Roots
| \(n\) | \(n^2\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
| 21 | 441 |
| 22 | 484 |
| 23 | 529 |
| 24 | 576 |
| 25 | 625 |
The squares in the “List of Squares” shown in Table \(\PageIndex{1}\) are called perfect squares. Each is the square of a whole number. But not all numbers are perfect squares. For example, in the case of \(\sqrt{24}\), there is no whole number whose square is equal to \(24\). However, this does not prevent \(\sqrt{24}\) from being a perfectly good number.
We can use the “List of Squares” to find decimal approximations when the radicand is not a perfect square.
Example \(\PageIndex{11}\)
Estimate \(\sqrt{24}\) by guessing. Use a calculator to find a more accurate result and compare this result with your guess.
Solution
From the “List of Squares,” note that \(24\) lies between \(16\) and \(25\), so \(\sqrt{24}\) will lie between \(4\) and \(5\), with \(\sqrt{24}\) much closer to \(5\) than it is to \(4\).

Let’s guess \[\sqrt{24}≈ 4.8\nonumber \]. As a check, let’s square \[4.8. (4.8)^2 = (4 .8)(4.8) = 23.04 \nonumber \] Not quite \(24\)! Clearly, \(\sqrt{24}\) must be a little bit bigger than \(4.8\).
Let’s use a scientific calculator to get a better approximation. From our calculator, using the square root button, we find \[\sqrt{24}≈ 4.89897948557 \nonumber \].
Even though this is better than our estimate of \(4.8\), it is still only an approximation. Our calculator was only capable of providing \(11\) decimal places. However, the exact decimal representation of \(\sqrt{24}\) is an infinite decimal that never terminates and never establishes a pattern of repetition.
Just for fun, here is a decimal approximation of \(\sqrt{24}\) that is accurate to \(1000\) places, courtesy of www.wolframalpha.com

If you were to multiply this number by itself (square the number), you would get a number that is extremely close to \(24\), but it would not be exactly \(24\). There would still be a little discrepancy.
Exercise \(\PageIndex{11}\)
Estimate: \(\sqrt{83}\)
- Answer
-
\(9.1\)
Reference
1 When we say that \(−36\) has no real square roots, we mean there are no real numbers that are square roots of \(−36\). The reason we emphasize the word real in this situation is the fact that \(−36\) does have two square roots that are elements of the complex numbers, a set of numbers that are usually introduced in advanced courses such as college algebra or trigonometry.


