4.3: Equations
- Page ID
- 49362
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Equations
An equation is a statement that two algebraic expressions are equal
An equation is composed of three parts.
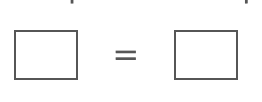
Each of the boxes represents an algebraic expression. An equation consists of two expressions separated by an equal sign. The equal sign makes the statement that the two expressions are equivalent, that is, they represent the same value. For example:
\(f = 32a\)
The equation expresses the relationship between the variables \(f\) and \(a\). It states that the value of \(f\) is always \(32\) times that of \(a\).
\(y = 6x + 8\)
The equation expresses the relationship between the variables \(x\) and \(y\). It states that the value of \(y\) is always \(8\) more than \(6\) times the value of \(x\).
Numerical Evaluation
Numerical evaluation is the process of determining a value by substituting numbers for letters.
Formulas
In various areas (business, statistics, physics, chemistry, astronomy, sociology, psychology, etc.), particular equations occur quite frequently. Such equations are called formulas. Numerical evaluation is used frequently with formulas.
Sample Set A
\(f = 32a\). Determine the value of \(f\) is \(a = 2\)
\(f = 32(2)\). Replace \(a\) by \(2\).
\( = 64\)
\(p = \dfrac{10,000}{v}\).
This chemistry equation expresses the relationship between the pressure \(p\) of a gas and the volume \(v\) of a gas.
Determine the value of \(p\) if \(v = 500\).
\(p = \dfrac{10,000}{500}\) Replace \(v\) by \(500\)
\(z = \dfrac{x-u}{s}\).
This statistics equation expresses the relationship between the variables \(z, x, u\), and \(s\). Determine the value of \(z\) is \(x = 41\), \(u = 45\), and \(s = 1.3\). Round to two decimal places.
\(\begin{aligned} z &=\dfrac{41-45}{1.3} \\ &=\dfrac{-4}{1.3} \\ &=-3.08 \end{aligned}\)
\(p = 5w^3 + w^2 - w - 1\).
This equation expresses the relationship between \(p\) and \(w\). Determine the value of \(p\) if \(w = 5\).
\(\begin{aligned} p &=5(5)^{3}+(5)^{2}-(5)-1 \\ &=5(125)+25-(5)-1 \\ &=625+25-5-1 \\ &=644 \end{aligned}\)
Practice Set A
\(f = 32a\). Determine the value of \(f\) if \(a = 6\).
- Answer
-
\(192\)
\(p = \dfrac{10,000}{v}\). Determine the value of \(p\) is \(v = 250\).
- Answer
-
\(40\)
\(F = \dfrac{9}{5}C + 32\). Determine the value of \(F\) if \(C = 10\)
- Answer
-
\(50\)
\(y = -9x - 14\). Determine the value of \(y\) if \(x = -3\).
- Answer
-
\(13\)
\(m = 5p^3 - 2p + 7\). Determine the value of \(m\) if \(p = -2\).
- Answer
-
\(-29\)
Exercises
For the following problems, observe the equations and state the relationship being expressed.
\(x = 6y\)
- Answer
-
The value of \(x\) is equal to six times the value of \(y\).
\(y = x + 4\)
\(e = g - 9\)
- Answer
-
\(e\) is equal to \(9\) less then the value of \(g\).
\(y = x - 7\)
\(3t = 6s\)
- Answer
-
The value of three times \(t\) is equal to six times \(s\).
\(u = v^5\)
\(r = \dfrac{2}{9}s\)
- Answer
-
The value of \(r\) is equal to two ninth times the value of \(s\).
\(b = \dfrac{3}{4}a\)
\(f = 0.97k + 55\)
- Answer
-
The value of \(f\) is equal to \(55\) more then \(\dfrac{97}{100}\) times the value of \(k\).
\(w = 4z^3 - 21\)
\(q^2 = 9x^8 + 2y\)
- Answer
-
The value of \(q^2\) is equal to nine times the value of \(x^8\) plus two times the value of \(y\).
\(I = m^2qb^5 + 3.115p\)
Use numerical evaluation on the equations for the following problems.
Geometry (circumference of a circle)
\(C = 2\pi r\). Find \(C\) if \(\pi\) is approximated by \(3.14\) and \(r = 5\)
- Answer
-
\(31.4\)
Geometry (area of a rectangle)
\(A = lw\). Find \(A\) if \(l = 15\) and \(w = 9\).
Electricity (current in a circuit)
\(I = \dfrac{E}{R}\). Find \(I\) if \(E = 21\) and \(R = 7\).
- Answer
-
\(3\)
Electricity (current in a circuit)
\(I = \dfrac{E}{R}\). Find \(I\) if \(E = 106\) and \(R = 8\).
Business (simple interest)
\(I = prt\). Find \(I\) if \(p = 3000\), \(r = 0.12\), and \(t = 1\).
- Answer
-
\(360\)
Business (simple interest)
\(I = prt\). Find \(I\) if \(p = 250\), \(r = 0.07\), and \(t = 6\).
Geometry (area of a parallelogram)
\(A = bh\). Find \(A\) if \(b = 16\) and \(h = 6\).
- Answer
-
\(96\)
Geometry (area of a triangle)
\(A = \dfrac{1}{2}bh\). Find \(A\) if \(b = 25\) and \(h = 10\).
Geometry (perimeter of a rectangle)
\(P = 2l + 2w\). Find \(P\) if \(l = 3\) and \(w = 1\).
- Answer
-
\(8\)
Geometry (perimeter of a rectangle)
\(P = 2l + 2w\). Find \(P\) if \(l = 74\) and \(w = 16\).
Geometry (perimeter of a rectangle)
\(P = 2l + 2w\). Find \(P\) if \(l = 8\dfrac{1}{4}\) and \(w = 12\dfrac{8}{9}\).
- Answer
-
\(42\dfrac{5}{18}\)
Physics (force)
\(F = 32m\). Find \(F\) if \(m = 6\).
Physics (force)
\(F = 32m\). Find \(F\) if \(m = 14\).
- Answer
-
\(448\)
Physics (force)
\(F = 32m\). Find \(F\) if \(m = 14\).
- Answer
-
\(448\)
Physics (force)
\(F = 32m\). Find \(F\) if \(m = 6.42\).
- Answer
-
\(205.44\)
Physics (momentum)
\(p = mv\). Find \(p\) if \(m = 18\) and \(v = 5\)
Physics (momentum)
\(p = mv\). Find \(p\) if \(m = 44\) and \(v = 9\)
- Answer
-
\(396\).
Physics (momentum)
\(p = mv\). Find \(p\) if \(m = 9.18\) and \(v = 16.5\)
Physics (energy)
\(E = \dfrac{1}{2}mv^2\). Find \(E\) if \(m = 12\) and \(v = 5\).
- Answer
-
\(150\)
Physics (energy)
\(E = \dfrac{1}{2}mv^2\). Find \(E\) if \(m = 8\) and \(v = 15\).
Physics (energy)
\(E = \dfrac{1}{2}mv^2\). Find \(E\) if \(m = 24.02\) and \(v = 7\).
- Answer
-
\(588.49\)
Astronomy (Kepler’s law of planetary motion)
\(P^2 = ka^3\). Find \(P^2\) if \(k = 1\) and \(a = 4\).
Astronomy (Kepler’s law of planetary motion)
\(P^2 = ka^3\). Find \(P^2\) if \(k = 8\) and \(a = 31\).
- Answer
-
238,328
Astronomy (Kepler’s law of planetary motion)
\(P^2 = ka^3\). Find \(P^2\) if \(k = 4\) and \(a = 5.1\).
Astronomy (Kepler’s law of planetary motion)
\(P^2 = ka^3\). Find \(P^2\) if \(k = 53.7\) and \(a = 0.7\).
- Answer
-
\(18.4191\)
Business (profit, revenue, and cost)
\(P = R - C\). Find \(P\) if \(R = 3100\) and \(C = 2500\).
Business (profit, revenue, and cost)
\(P = R - C\). Find \(P\) if \(R = 4240\) and \(C = 3590\).
- Answer
-
\(650\)
Geometry (area of a circle)
\(A = \pi r^2\). Find \(A\) if \(\pi\) is approximately \(3.14\) and \(r = 3\).
Geometry (area of a circle)
\(A = \pi r^2\). Find \(A\) if \(\pi\) is approximately \(3.14\) and \(r = 11\).
- Answer
-
\(379.94\)
\(t = 21x + 6\). Find \(t\) if \(x = 3\)
\(t = 21x + 6\). Find \(t\) if \(x = 97\)
- Answer
-
\(2,043\)
\(E = mc^2\). Find \(E\) if \(m = 2\) and \(c = 186,000\).
\(E = mc^2\). Find \(E\) if \(m = 5\) and \(c = 186,000\).
- Answer
-
\(1.7298 \times 10^{11}\).
An object travels on a horizontal line. The distance it travels is represented by \(d\) and is measured in meters. The equation relating time of travel, \(t\), and distance of travel, \(d\), is
\(d=t2−4t+20\)
Determine the distance traveled by the object if it has been in motion for \(6\) seconds.
In medicine, there are several rules of thumb used by physicians to determine a child’s dose, \(D_c\), of a particular drug. One such rule, Young’s Rule, relates a child’s dose of a drug to an adult’s dose of that drug, \(D_a\). Young’s Rule is
\(D_c = \dfrac{t}{t+12} \cdot D_a\)
where \(t\) is the child's age in years. What does should be given to a child 8 years old if the corresponding adult dosage is 15 units?
- Answer
-
6 units
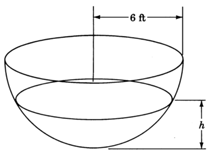
A hemispherical water tank of radius \(6\) feet has water dripping into it. The equation relating the volume, \(V\), of water in the tank at any time is \(V=6\pi h^2−\pi 3h^3\),where \(h\) represents the depth of the water. Using \(3.14\) to approximate the irrational number \(\pi\), determine the volume of water in the tank when the depth of the water is \(3\) feet.
The equation \(W=3.51L−192\) has been established by the International Whaling Commission to relate the weight, \(W\) (in long tons), of a mature blue whale to its length, \(L\) (in feet). The equation is only used when \(L \ge 70\). When
\(0<L<70\)
blue whales are considered immature. At birth, a blue whale is approximately \(24\) feet long. Determine the weight of a blue whale that measures \(83\) feet in length.
- Answer
-
\(99.33\) tons
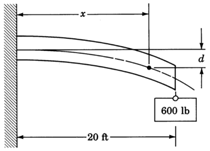
A relationship exists between the length of a cantilever beam and the amount it is deflected when a weight is attached to its end. If a cantilever beam \(20\) feet long has a \(600\) pound weight attached to its end, the equation relating beam length and amount of deflection is
\(d = \dfrac{60x^2-x^3}{16,000}\)
where \(d\) is the amount of deflection measured in inches and \(x\) is the length from the supported part of the beam to some point on the beam at which the amount of deflection is measured. Find the amount of deflection of the beam \(17\) feet from the supported end.
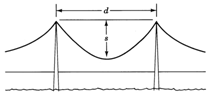
There is a relationship between the length of a suspension bridge cable that is secured between two vertical supports and the amount of sag of the cable. If we represent the length of the cable by \(c\), the horizontal distance between the vertical supports by \(d\), and the amount of sag by \(s\), the equation is \(c=d + \dfrac{8s^2}{3d} - \dfrac{32s^4}{5d^3}\). If the horizontal distance between the two vertical supports is \(190\) feet and the amount of sag in a cable that is suspended between the two supports is \(20\) feet, what is the length of the cable?
- Answer
-
\(195.46474\)
Exercises for Review
Simplify \((4x^3y^8)(3x^2y)\)
Simplify \(-|-8|\)
- Answer
-
\(-8\)
Find the value of \(4^{-2} \cdot 8^2 - 3^2\).
For the expression \(5(a + b) + 2x^2\), write the number of terms that appear and then write the terms themselves.
- Answer
-
\(2; 5(a + b), 2x^2\)
How many \(xy^3\)'s are there in \(5x^2y^5\)?


