4.6: Combining Polynomials Using Multiplication
- Page ID
- 49365
Multiplying a Polynomial by a Monomial
Multiplying a polynomial by a monomial is a direct application of the distributive property.
Distributive Property
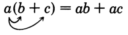
The distributive property suggests the following rule.
To multiply a polynomial by a monomial, multiply every term of the polynomial by the monomial and then add the resulting products together.
Sample Set A
\(\begin{aligned}
3(x+9) &=3 \cdot x+3 \cdot 9 \\
&=3 x+27
\end{aligned}\)
\(\begin{aligned}
6\left(x^{3}-2 x\right)=6\left(x^{3}+(-2 x)\right) &=6 \cdot x^{3}+6(-2 x) \\
&=6 x^{3}-12 x
\end{aligned}\)
\(\begin{aligned}
(x-7) x &=x \cdot x+x(-7) \\
&=x^{2}-7 x
\end{aligned}\)
\(\begin{aligned}
8 a^{2}\left(3 a^{4}-5 a^{3}+a\right) &=8 a^{2} \cdot 3 a^{4}+8 a^{2}\left(-5 a^{3}\right)+8 a^{2} \cdot a \\
&=24 a^{6}-40 a^{5}+8 a^{3}
\end{aligned}\)
\(\begin{aligned}
4 x^{2} y^{7} z\left(x^{6} y+8 y^{2} z^{2}\right) &=4 x^{2} y^{7} z \cdot x^{5} y+4 x^{2} y^{7} z \cdot 8 y^{2} z^{2} \\
&=4 x^{7} y^{8} z+32 x^{2} y^{9} z^{3}
\end{aligned}\)
\(10 a b^{2} c\left(125 a^{2}\right)=1250 a^{3} b^{2} c\)
\(\begin{aligned}
\left(9 x^{2} z+4 w\right)\left(5 z w^{3}\right) &=9 x^{2} z \cdot 5 z w^{3}+4 w \cdot 5 z w^{3} \\
&=45 x^{2} z^{2} w^{3}+20 z w^{4} \\
&=45 x^{2} w^{3} z^{2}+20 w^{4} z
\end{aligned}\)
Practice Set A
Determine the following products.
\(3(x + 8)\)
- Answer
-
\(3x+24\)
\((2+a)4\)
- Answer
-
\(4a+8\)
\((a^2 - 2b + 6)2a\)
- Answer
-
\(2a^3 - 4ab + 12a\)
\(8a^2b^3(2a + 7b + 3)\)
- Answer
-
\(16a^3b^3 + 56a^2b^4 + 24a^2b^3\)
\(4x(2x^5 + 6x^4 - 8x^3 - x^2 + 9x - 11)\)
- Answer
-
\(8x^6 + 24x^5 - 32x^4 - 4x^3 + 36x^2 - 44x\)
\((3a^2b)(2ab^2 + 4b^3)\)
- Answer
-
\(6a^3b^3 + 12a^2b^4\)
\(5mn(m^2n^2 + m + n^0), n \not = 0\)
- Answer
-
\(5m^3n^3 + 5m^2n + 5mn\)
\(6.03(2.11a^3 + 8.00a^2b)\)
- Answer
-
\(12.7233a^3 + 48.24a^2b\)
Simplifying \(+(a+b)\) and \(−(a+b)\)
\(+(a+b)\) and \(−(a+b)\)
Oftentimes, we will encounter multiplications of the form
\(+1(a+b)\) or \(−1(a+b)\)
These terms will actually appear as
\(+(a+b)\) and \(−(a+b)\)
Using the distributive property, we can remove the parentheses.
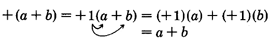
The parentheses have been removed and the sign of each term has remained the same.
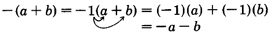
The parentheses have been removed and the sign of each term has been changed to its opposite.
- To remove a set of parentheses preceded by a "+" sign, simply remove the parentheses and leave the sign of each term the same.
- To remove a set of parentheses preceded by a “−” sign, remove the parentheses and change the sign of each term to its opposite sign.
Sample Set B
Simplify the expressions.
\((6x−1)\).
This set of parentheses is preceded by a “\(+\)’’ sign (implied). We simply drop the parentheses.
\((6x−1)=6x−1\)
\((14a^2 - 6a^3b^2 + ab^4) = 14a^2b^3 - 6a^3b^2 + ab^4\)
\(-(21a^2 + 7a - 18)\)
This set of parentheses is preceded by a “\(−\)” sign. We can drop the parentheses as long as we change the sign of every term inside the parentheses to its opposite sign.
\(-(21a^2 + 7a - 18) = -21a^2 - 7a + 18\)
\(-(7y^3 - 2y^2 + 9y + 1) = -7y^3 + 2y^2 - 9y - 1\)
Practice Set B
Simplify by removing the parentheses.
\((2a+3b)\)
- Answer
-
\(2a + 3b\)
\((a^2 - 6a + 10)\)
- Answer
-
\(a^2 - 6a + 10\)
\(−(x+2y)\)
- Answer
-
\(−x−2y\)
\(−(5m−2n)\)
- Answer
-
\(−5m+2n\)
\(-(-3s^2 - 7s + 9)\)
- Answer
-
\(3s^2 + 7s - 9\)
Multiplying a Polynomial by a Polynomial
Since we can consider an expression enclosed within parentheses as a single quantity, we have, by the distributive property,
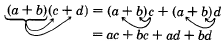
For convenience, we will use the commutative property of addition to write this expression so that the first two terms contain a and the second two contain b.
\((a+b)(c+d)=ac+ad+bc+bd\)
This method is commonly called the FOIL method.
- F: First Terms
- O: Outer Terms
- I: Inner Terms
- L: Last Terms
\((a+b)(2+3)=\underbrace{(a+b)+(a+b)}_{2 \text { terms }}+\underbrace{(a+b)+(a+b)+(a+b)}_{3 \text { terms }}\)
Rearranging,
\(\begin{array}{l}
=a+a+b+b+a+a+a+b+b+b \\
=2 a+2 b+3 a+3 b
\end{array}\)
Combining like terms,
\(\begin{array}{l}
=5a + 5b
\end{array}\)
This use of the distributive property suggests the following rule.
To multiply two polynomials together, multiply every term of one polynomial by every term of the other polynomial.
Sample Set C
Perform the following multiplications and simplify.
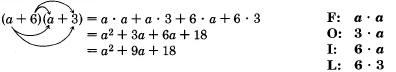
With some practice, the second and third terms can be combined mentally.
\(\begin{aligned}
(m-3)^{2} &=(m-3)(m-3) \\
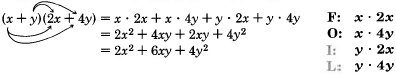
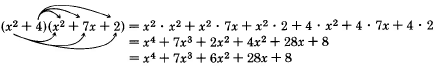
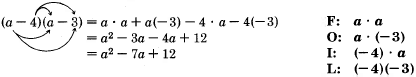
&=m \cdot m+m(-3)-3 \cdot m-3(-3) \\
&=m^{2}-3 m-3 m+9 \\
&=m^{2}-6 m+9
\end{aligned}\)
\(\begin{aligned}
(x+5)^{3} &=(x+5)(x+5)(x+5) & \text { Associate the first two factors. } \\
&=[(x+5)(x+5)](x+5) \\
&=\left[x^{2}+5 x+5 x+25\right](x+5) \\
&=\left[x^{2}+10 x+25\right](x+5) \\
&=x^{2} \cdot x+x^{2} \cdot 5+10 x \cdot x+10 x \cdot 5+25 \cdot x+25 \cdot 5 \\
&=x^{3}+5 x^{2}+10 x^{2}+50 x+25 x+125 \\
&=x^{3}+15 x^{2}+75 x+125
\end{aligned}\)
Practice Set C
Find the following products and simplify.
\((a+1)(a+4)\)
- Answer
-
\(a^2 + 5a + 4\)
\((m−9)(m−2)\)
- Answer
-
\(m^2 - 11m + 18\)
\((2x+4)(x+5)\)
- Answer
-
\(2x^2 + 14x + 20\)
\((x+y)(2x−3y)\)
- Answer
-
\(2x^2 - xy - 3y^2\)
\((3a^2 - 1)(5a^2 + a)\)
- Answer
-
\(15a^4 + 3a^3 - 5a^2 - a\)
\((2x^2y^3 + xy^2)(5x^3y^2 + x^2y)\)
- Answer
-
\(10x^5y^5 + 7x^4y^4 + x^3y^3\)
\((a+3)(a^2+3a+6)\)
- Answer
-
\(a^3 + 6a^2 + 15a + 18\)
\((a+4)(a+4)\)
- Answer
-
\(a^2 + 8a + 16\)
\((r−7)(r−7)\)
- Answer
-
\(r^2 - 14r + 49\)
\((x+6)^2\)
- Answer
-
\(x^2 + 12x + 36\)
\((y-8)^2\)
- Answer
-
\(y^2 - 16y + 64\)
Sample Set D
Perform the following additions and subtractions.
\(3x+7+(x-3)\). We must first remove the parentheses. They are preceded by a "\(+\)" sign, so we remove them and leave the sign of each term the same.
\(3x+7+x-3\) Combine like terms.
\(4x+4\)
\(5 y^{3}+11-\left(12 y^{3}-2\right)\). We first remove the parentheses. They are preceded by a "\(-\)" sign, so we remove them and change the sign of each term inside them.
\(5y^{3}+11-12 y^{3}+2\) Combine like terms.
\(-7y^{3}+13\)
Add \(4x^2 + 2x - 8\) to \(3x^2 - 7x - 10\)
\(\begin{array}{l}
\left(4 x^{2}+2 x-8\right)+\left(3 x^{2}-7 x-10\right) \\
4 x^{2}+2 x-8+3 x^{2}-7 x-10 \\
7 x^{2}-5 x-18
\end{array}\)
Subtract \(8x^2 - 5x + 2\) from \(3x^2 + x - 12\).
\(\begin{array}{l}
\left(3 x^{2}+x-12\right)-\left(8 x^{2}-5 x+2\right) \\
3 x^{2}+x-12-8 x^{2}+5 x-2 \\
-5 x^{2}+6 x-14
\end{array}\)
Be very careful not to write this problem as:
\(3x^2 + x - 12 - 8x^2 - 5x + 2\)
This form has us subtracting only the very first term, \(8x^2\), rather than the entire expression. Use parentheses.
Another incorrect form is:
\(8x^2 - 5x + 2 - (3x^2 + x - 12)\)
This form has us performing the subtraction in the wrong order.
Practice Set D
Perform the following additions and subtractions.
\(6y^2 + 2y - 1 + (5y^2 - 18)\)
- Answer
-
\(11y^2 + 2y - 19\)
\((9m−n)−(10m+12n)\)
- Answer
-
\(−m−13n\)
Add \(2r^2 + 4r - 1\) to \(3r^2 - r - 7\)
- Answer
-
\(5r^2 + 3r - 8\)
Subtract \(4s−3\) from \(7s+8\).
- Answer
-
Add texts here. Do not delete this text first.
Exercises
For the following problems, perform the multiplication and combine any like terms.
\(7(x+6)\)
- Answer
-
\(7x+42\)
\(4(y+3)\)
\(6(y+4)\)
- Answer
-
\(6y+24\)
\(8(m+7)\)
\(5(a−6)\)
- Answer
-
\(5a−30\)
\(2(x−10)\)
\(3(4x+2)\)
- Answer
-
\(12x+6\)
\(6(3x+4)\)
\(9(4y−3)\)
- Answer
-
\(36y−27\)
\(5(8m−6)\)
\(−9(a+7)\)
- Answer
-
\(−9a−63\)
\(−3(b+8)\)
\(−4(x+2)\)
- Answer
-
\(−4x−8\)
\(−6(y+7)\)
\(−3(a−6)\)
- Answer
-
\(−3a+18\)
\(−9(k−7)\)
\(−5(2a+1)\)
- Answer
-
\(−10a−5\)
\(−7(4x+2)\)
\(−3(10y−6)\)
- Answer
-
\(−30y+18\)
\(−8(4y−11)\)
\(x(x+6)\)
- Answer
-
\(x^2 + 6x\)
\(y(y+7)\)
\(m(m−4)\)
- Answer
-
\(m^2 - 4m\)
\(k(k−11)\)
\(3x(x+2)\)
- Answer
-
\(3x^2 + 6x\)
\(4y(y+7)\)
\(6a(a−5)\)
- Answer
-
\(6a^2 - 30a\)
\(9x(x−3)\)
\(3x(5x+4)\)
- Answer
-
\(15x^2 + 12x\)
\(4m(2m+7)\)
\(2b(b−1)\)
- Answer
-
\(2b^2 - 2b\)
\(7a(a−4)\)
\(3x^2(5x^2 + 4)\)
- Answer
-
\(15x^4 + 12x^2\)
\(9y^3(3y^2 + 2)\)
\(4a^4(5a^3 + 3a^2 + 2a)\)
- Answer
-
\(20a^7 + 12a^6 + 8a^5\)
\(2x^4(6x^3 - 5x^2 - 2x + 3)\)
\(-5x^2(x + 2)\)
- Answer
-
\(-5x^3 - 10x^2\)
\(-6y^3(y + 5)\)
\(2x^2y(3x^2y^2 - 6x)\)
- Answer
-
\(6x^4y^3 - 12x^3y\)
\(8a^3b^2c(2ab^3 + 3b)\)
\(b^5x^2(2bx - 11)\)
- Answer
-
\(2b^6x^3 - 11b^5x^2\)
\(4x(3x^2-6x+10)\)
\(9y^3(2y^4 - 3y^3 + 8y^2 + y - 6)\)
- Answer
-
\(18y^7 - 27y^6 + 72y^5 + 9y^4 - 54y^3\)
\(-a^2b^3(6ab^4 + 5ab^3 - 8b^2 + 7b - 2)\)
\((a+4)(a+2)\)
- Answer
-
\(a^2 + 6a + 8\)
\((x+1)(x+7)\)
\((y+6)(y−3)\)
- Answer
-
\(y^2 + 3y - 18\)
\((t+8)(t−2)\)
\((i−3)(i+5)\)
- Answer
-
\(i^2 + 2i - 15\)
\((x−y)(2x+y)\)
\((3a−1)(2a−6)\)
- Answer
-
\(6a^2 - 20a + 6\)
\((5a−2)(6a−8)\)
\((6y+11)(3y+10)\)
- Answer
-
\(18y^2 + 93y + 110\)
\((2t+6)(3t+4)\)
\((4+x)(3−x)\)
- Answer
-
\(-x^2 - x + 12\)
\((6+a)(4+a)\)
\((x^2 + 2)(x + 1)\)
- Answer
-
\(x^3 + x^2 + 2x + 2\)
\((x^2 + 5)(x + 4)\)
\((3x^2 - 5)(2x^2 + 1)\)
- Answer
-
\(6x^4 - 7x^2 - 5\)
\((4a^2b^3 - 2a)(5a^2b - 3b)\)
\((6x^3y^4 + 6x)(2x^2y^3 + 5y)\)
- Answer
-
\(12x^5y^7 + 30x^3y^5 + 12x^3y^3 + 30xy\)
\(5(x−7)(x−3)\)
\(4(a+1)(a−8)\)
- Answer
-
\(4a^2 - 28a - 32\)
\(a(a−3)(a+5)\)
\(x(x+1)(x+4)\)
- Answer
-
\(x^3 + 5x^2 + 4x\)
\(y^3(y-3)(y-2)\)
- Answer
-
\(y^5 - 5y^4 + 6y^3\)
\(2a^2(a + 4)(a + 3)\)
\(5y^6(y + 7)(y + 1)\)
- Answer
-
\(5y^8 + 40y^7 + 35y^6\)
\(ab^2(a^2 - 2b)(a + b^4)\)
\(x^3y^2(5x^2y^2 - 3)(2xy - 1)\)
- Answer
-
\(10x^6y^5 - 5x^5y^4 - 6x^4y^3 + 3x^3y^2\)
\(6(a^2 + 5a + 3)\)
\(8(c^3 + 5c + 11)\)
- Answer
-
\(8c^3 + 40c + 88\)
\(3a^2(2a^3 - 10a^2 - 4a + 9)\)
\(6a^3b^3(4a^2b^6 + 7ab^8 + 2b^{10} +14)\)
- Answer
-
\(24a^5b^9 + 42a^4b^{11} + 12a^3b^{13}+18a^3b^3\)
\((a-4)(a^2 + a - 5)\)
\((x-7)(x^2 + x - 3)\)
- Answer
-
\(x^3 - 6x^2 - 10x + 21\)
\((2x + 1)(5x^3 + 6x^2 + 8)\)
\((7a^2 + 2)(3a^5 - 4a^3 - a - 1)\)
- Answer
-
\(21a^7 - 22a^5 - 15a^3 - 7a^2 - 2a - 2\)
\((x+y)(2x^2 + 3xy + 5y^2)\)
\((2a+b)(5a^2 + 4a^2b - b - 4)\)
- Answer
-
\(10a^3 + 8a^3b + 4a^2b^2 + 5a^2b - b^2 - 8a - 4b - 2ab\)
\((x+3)^2\)
\((x+1)^2\)
- Answer
-
\(x^2 + 2x + 1\)
\((x-5)^2\)
\((a+2)^2\)
- Answer
-
\(a^2 + 4a + 4\)
\((a-9)^2\)
\(-(3x-5)^2\)
- Answer
-
\(-9x^2 + 30x - 25\)
\(-(8t+7)^2\)
For the following problems, perform the indicated operations and combine like terms.
\(3x^2 + 5x - 2 + (4x^2 - 10x - 5)\)
- Answer
-
\(7x^2 - 5x - 7\)
\(-2x^3 + 4x^2 + 5x - 8 + (x^3 - 3x^2 - 11x + 1)\)
\(-5x - 12xy + 4y^2 + (-7x + 7xy - 2y^2)\)
- Answer
-
\(2y^2 - 5xy - 12x\)
\((6a^2 - 3a + 7) - 4a^2 + 2a - 8\)
\((5x^2 - 24x - 15) + x^2 - 9x + 14\)
- Answer
-
\(6x^2 - 33x - 1\)
\((3x^3 - 7x^2 + 2) + (x^3 + 6)\)
\((9a^2b - 3ab + 12ab^2) + ab^2 + 2ab\)
- Answer
-
\(9a^2b + 13ab^2 - ab\)
\(6x^2 - 12x + (4x^2 - 3x - 1) + 4x^2 - 10x - 4\)
\(5a^3 - 2a - 26 + (4a^3 - 11a^2 + 2a) - 7a + 8a^3 + 20\)
- Answer
-
\(17a^3 - 11a^2 - 7a - 6\)
\(2xy - 15 - (5xy + 4)\)
Add \(4x + 6\) to \(8x - 15\).
- Answer
-
\(12x - 9\)
Add \(5y^2 - 5y + 1\) to \(-9y^2 + 4y - 2\)
Add \(3(x+6)\) to \(4(x-7)\)
- Answer
-
\(7x - 10\)
Add \(-2(x^2 - 4)\) to \(5(x^2 + 3x - 1)\)
Add four times \(5x + 2\) to three times \(2x - 1\)
- Answer
-
\(26x + 5\)
Add five times \(-3x + 2\) to seven times \(4x + 3\)
Add \(-4\) times \(9x + 6\) to \(-2\) times \(-8x - 3\).
- Answer
-
\(-20x - 18\)
Subtract \(6x^2 - 10x + 4\) from \(3x^2 - 2x + 5\)
Subtract \(a^2 - 16\) from \(a^2 - 16\)
- Answer
-
\(0\)
Exercises for Review
Simplify \((\dfrac{15x^2y^4}{5xy^2})^4\)
Express the number \(198,000\) using scientific notation.
- Answer
-
\(1.98 \times 10^5\)
How many \(4a^2x^3\)'s are there in \(-16a^4x^5\)?
State the degree of the polynomial \(4xy^3 + 3x^5y - 5x^3y^3\), and write the numerical coefficient of each term.
- Answer
-
Degree is 6; 4, 3, -5
Simplify \(3(4x-5) + 2(5x-2) - (x-3)\).