4.5: Combining Polynomials Using Addition and Subtraction
( \newcommand{\kernel}{\mathrm{null}\,}\)
Like Terms
Like Terms
Terms whose variable parts, including the exponents, are identical are called like terms. Like terms is an appropriate name since terms with identical variable parts and different numerical coefficients represent different amounts of the same quantity. As long as we are dealing with quantities of the same type we can combine them using addition and subtraction.
An algebraic expression can be simplified by combining like terms.
Sample Set A
Combine the like terms.
6 houses + 4 houses = 10 houses. 6 and 4 are the same type give 10 of that type.
6 houses + 4 houses+ 2 motels = 10 houses + 2 motels . 6 and 4 of the same type give 10 of that type. Thus, we have 10 of one type and 2 of another type.
Suppose we let the letter x represent "house." Then, 6x+4x=10x. 6 and 4 of the same type give 10 of that type.
Suppose we let x represent "house" and y represent "motel."
6x+4x+2y=10x+2y
Practice Set A
Like terms with the same numerical coefficient represent equal amounts of the same quantity.
Like terms with different numerical coefficients represent
- Answer
-
different amounts of the same quantity
Combining Like Terms
Since like terms represent amounts of the same quantity, they may be combined, that is, like terms may be added together.
Simplify each of the following polynomials by combining like terms.
2x+5x+3x.
There are 2x's, then 5 more, then 3 more. This makes a total iof 10x's.
7x+8y−3x.
From 7x's, we lose 3x's. This makes 4x's. The 8y's represent a quantity different from the x's and therefore will not combine with them.
7x+8y−3x=4x+8y.
4a3−2a2+8a3+a2−2a3.
4a3,8a3, and −2a3 represent quantities of the same type.
4a3+8a3−2a3=10a3.
−2a2 and a2 represent quantities of the same type.
−2a2+a2=−a2.
Thus,
4a3−2a2+8a3+a2−2a3=10a3−a2.
Practice Set B
Simplify each of the following expressions.
4y+7y
- Answer
-
11y
3x+6x+11x
- Answer
-
20x
5a+2b+4a−b−7b
- Answer
-
9a−6b
10x3−4x3+3x2−12x3+5x2+2x+x3+8x
- Answer
-
−5x3+8x2+10x
2a5−a5+1−4ab−9+9ab−2−3−a5.
- Answer
-
5ab−13.
Simplifying Expressions Containing Parentheses
Simplifying Expressions Containing Parentheses
When parentheses occur in expressions, they must be removed before the expression can be simplified. Parentheses can be removed using the distributive property.
Distributive Property
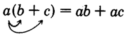
Sample Set C
Simplify each of the following expressions by using the distributive property and combining like terms.
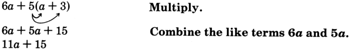
4x+9(x2−6x−2)+5 Remove parentheses.
4x+9x2−54x−18+5 Combine like terms.
−50x+9x2−13
By convention, the terms in an expression are placed in descending order with the highest degree term appearing first. Numerical terms are placed at the right end of the expression. The commutative property of addition allows us to change the order of the terms.
9x2−50x−13
2+2[5+4(1+a)]
Eliminate the innermost set of parentheses first
2+2[5+4+4a]
By the order of operations, simplify inside the parentheses before multiplying (by the 2)
2+2[9+4a] Remove this set of parentheses.
2+18+8a Combine like terms.
20+8a Write in descending order.
8a+20
x(x−3)+6x(2x+3)
Use the rule for multiplying powers with the same base.
x2−3x+12x2+18x Combine like terms.
13x2+15x
Practice Set C
Simplify each of the following expressions by using the distributive property and combining like terms.
4(x+6)+3(2+x+3x2)−2x2
- Answer
-
7x2+7x+30
7(x+x3)−4x3−x+1+4(x2−2x3+7)
- Answer
-
−5x3+4x2+6x+29
5(a+2)+6a−7+(8+4)(a+3a+2)
- Answer
-
59a+27
x(x+3)+4x2+2x
- Answer
-
5x2+5x
a3(a2+a+5)+a(a4+3a2+4)+1
- Answer
-
2a5+a4+8a3+4a+1
2[8−3(x−3)]
- Answer
-
−6x+34
x2+3x+7[x+4x2+3(x+x2)]
- Answer
-
50x2+31x
Exercises
For the following problems, simplify each of the algebraic expressions.
x+3x
- Answer
-
4x
4x+7x
9a+12a
- Answer
-
21a
5m−3m
10x−7x
- Answer
-
3x
7y−9y
6k−11k
- Answer
-
−5k
3a+5a+2a
9y+10y+2y
- Answer
-
21y
5m−7m−2m
h−3h−5h
- Answer
-
−7h
a+8a+3a
7ab+4ab
- Answer
-
11ab
8ax+2ax+6ax
3a2+6a2+2a2
- Answer
-
11a2
14a2b+4a2b+19a2b
10y−15y
- Answer
-
−5y
7ab−9ab+4ab
210ab4+412ab4+100a4b (Look closely at the exponents.)
- Answer
-
622ab4+100a4b
5x2y0+3x2y+2x2y+1,y≠0 (Look closely at the exponents.)
8w2−12w2−3w2
- Answer
-
−7w2
6xy−3xy+7xy−18xy
7x3−2x2−10x+1−5x2−3x3−12+x
- Answer
-
4x3−7x2−9x−11
21y−15x+40xy−6−11y+7−12x−xy
1x+1y−1x−1y+x−y
- Answer
-
x−y
5x2−3x−7+2x2−x
−2z+15z+4z3+z2−6z2+z
- Answer
-
2z3−5z2+16z
18x2y−14x2y−20x2y
−9w5−9w4−9w5+10w4
- Answer
-
−18w5+w4
2x4+4x3−8x2+12x−1−7x3−1x4−6x+2
17d3r+3d3r−5d3r+6d2r+d3r−30d2r+3−7+2
- Answer
-
16d3r−24d2r−2
a0+2a0−4a0,a≠0
4x0+3x0−5x0+7x0−x0,x≠0
- Answer
-
8
2a3b2c+3a2b2c0+4a2b2−a3b2c,c≠0
3z−6z+8z
- Answer
-
5z
3z2−z+3z3
6x3+12x+5
- Answer
-
6x3+12x+5
3(x+5)+2x
7(a+2)+4
- Answer
-
7a+18
y+5(y+6)
2b+6(3−5b)
- Answer
-
−28b+18
5a−7c+3(a−c)
8x−3x+4(2x+5)+3(6x−4)
- Answer
-
31x+8
2z+4ab+5z−ab+12(1−ab−z)
(a+5)4+6a−20
- Answer
-
10a
(4a+5b−2)3+3(4a+5b−2)
(10x+3y2)4+4(10x+3y2)
- Answer
-
80x+24y2
2(x−6)+5
1(3x+15)+2x−12
- Answer
-
5x+3
1(2+9a+4a2)+a2−11a
1(2x−6b+6a2b+8b2)+1(5x+2b−3a2b
- Answer
-
3a2b+8b2−4b+7x
After observing the following problems, can you make a conjecture about 1(a+b)?
1(a+b) =
Using the result of problem 52, is it correct to write
(a+b)=a+b?
- Answer
-
yes
3(2a+2a2)+8(3a+3a2)
x(x+2)+2(x2+3x−4
- Answer
-
3x2+8x−8
A(A+7)+4(A2+3a+1)
b(2b3+5b2+b+6)−6b2−4b+2
- Answer
-
2b4+5b3−5b2+2b+2
4a−a(a+5)
x−3x(x2−7x−1)
- Answer
-
−3x3+21x2+4x
ab(a−5)−4a2b+2ab−2
xy(3xy+2x−5y)−2x2y2−5x2y+4xy2
- Answer
-
x2y2−3x2y−xy2
3h[2h+5(h+2)]
2k[5k+3(1+7k)]
- Answer
-
52k2+6k
8a[2a−4ab+9(a−5−ab)]
6m+5n[n+3(n−1)]+2n2−4n2−9m
- Answer
-
128n2−90n−3m
5[4(r−2s)−3r−5s]+12s
89[b−2a+6c(c+4)−4c2]+4a+b−3b
- Answer
-
144c2−112a+77b+1728c
5[4(6x−3)+x]−2x−25x+4
3xy2(4xy+5y)+2xy3+6x2y3+4y3−12xy3
- Answer
-
18x2y3+5xy3+4y3
9a3b7(a3b5−2a2b2+6)−2a(a2b7−5a5b12+3a4b9)−a3b7
−8(3a+2)
- Answer
-
−24a−16
−4(2x−3y)
−4xy2[7xy−6(5−xy2)+3(−xy+1)+1]
- Answer
-
−24x2y4−16x2y3+104xy2
Exercises for Review
Simplify (x10y8z2x2y6)3
Find the value of −3(4−9)−6(−3)−123
- Answer
-
4
Write the expression 42x2y5z321x4y7 so that no denominator appears.
How many (2a+5)'s are there in 3x(2a+5)
- Answer
-
3x
Simplify 3(5n+6m2)−2(3n+4m2)


