4.7: Special Binomial Products
- Page ID
- 58529
Three binomial products occur so frequently in algebra that we designate them as special binomial products. We have seen them before, but we will study them again because of their importance as time saving devices and in solving equations (which we will study in a later chapter).
These special products can be shown as the squares of a binomial
\((a+b)^2\) and \((a-b)^2\)
and as the sum and difference of two terms.
\[(a+b)(a-b) \nonumber\]
There are two simple rules that allow us to easily expand (multiply out) these binomials. They are well worth memorizing, as they will save a lot of time in the future.
Expanding \((a+b)^2\) and \((a−b)^2\)
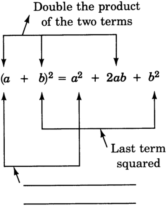
To square a binomial:
- Square the first term.
- Take the product of the two terms and double it.
- Square the last term.
- Add the three results together
\((a+b)^2 = a^2 + 2ab + b^2\)
\((a-b)^2 = a^2 - 2ab + b^2\)
Expanding (a+b)(a−b)
To expand the sum and difference of two terms:†
- Square the first term and square the second term.
- Subtract the square of the second term from the square of the first term.
\((a+b)(a-b) = a^2 - b^2\)
Sample Set A
\((x+4)^{2}\)
Square the first term: \(x^{2}\).
The product of both terms is \(4x\). Double it: \(8x\).
Square the last term: 16.
Add them together: \(x^{2}+8x+16\)
\((x+4)^{2}=x^{2}+8 x+16\)
Note that \((x+4)^{2} \neq x^{2}+4^{2}\). The \(8x\) term is missing!
\((a-8)^{2}\)
Square the first term: \(a^{2}\).
The product of both terms is \(-8a\). Double it: \(-16a\).
Square the last term: 64.
Add them together: \(a^2 + (-16a) + 64\)
\[(a-8)^2 = a^2 - 16a + 64 \nonumber\]
Notice that the sign of the last term in this expression is “\(+\).” This will always happen since the last term results from a number being squared. Any nonzero number times itself is always positive.
\((+)(+) = +\) and \((-)(-) = +\)
The sign of the second term in the trinomial will always be the sign that occurs inside the parentheses.
\((y-1)^{2}\)
Square the first term: \(y^{2}\).
The product of both terms is \(-y\). Double it: \(-2y\).
Square the last term: +1.
Add them together: \(y^2 + (-2y) + 1\)
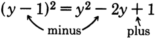
\((5x+3)^{2}\)
Square the first term: \(25x^{2}\).
The product of both terms is \(15x\). Double it: \(30x\).
Square the last term: 9.
Add them together: \(25x^2 + 30x + 9\)
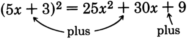
\((7b-2)^{2}\)
Square the first term: \(49b^{2}\).
The product of both terms is \(-14b\). Double it: \(-28b\).
Square the last term: 4.
Add them together: \(49b^2 + (-28b) + 4\)
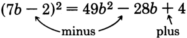
\((x+6)(x-6)\)
Square the first term: \(x^2\).
Subtract the square of the second term (\(36\)) from the square of the first term: \(x^2 - 36\)
\((x+6)(x-6) = x^2 - 36\)
\((4a−12)(4a+12)\)
Square the first term: \(16a^2\).
Subtract the square of the second term (\(144\)) from the square of the first term: \(16a^2-144\)
\((4a-12)(4a+12) = 16a^2 - 144\)
\((6x+8y)(6x−8y)\)
Square the first term: \(36x^2\).
Subtract the square of the second term (\(64y^2\)) from the square of the first term: \(36x^2 - 64y^2\)
\((6x+8y)(6x-8y) = 36x^2 - 64y^2\)
Practice Set A
Find the following products.
\((x+5)^2\)
- Answer
-
\(x^2 + 10x + 25\)
\((x+7)^2\)
- Answer
-
\(x^2 + 14x + 49\)
\((y-6)^2\)
- Answer
-
\(y^2 - 12y + 36\)
\((3a+b)^2\)
- Answer
-
\(9a^2 + 6ab + b^2\)
\((9m-n)^2\)
- Answer
-
\(81m^2 - 18mn + n^2\)
\((10x - 2y)^2\)
- Answer
-
\(100x^2 - 40xy + 4y^2\)
\((12a - 7b)^2\)
- Answer
-
\(144a^2 - 168ab + 49b^2\)
\((5h - 15k)^2\)
- Answer
-
\(25h^2 - 150hk + 225k^2\)
Exercises
For the following problems, find the products.
\((x+3)^2\)
- Answer
-
\(x^2 + 6x + 9\)
\((x+5)^2\)
\((x+8)^2\)
- Answer
-
\(x^2 + 16x + 64\)
\((x+6)^2\)
\((y+9)^2\)
- Answer
-
\(y^2 + 18y + 81\)
\((y+1)^2\)
\((a-4)^2\)
- Answer
-
\(a^2 - 8a + 16\)
\((a-6)^2\)
\((a-7)^2\)
- Answer
-
\(a^2 - 14a + 49\)
\((b+10)^2\)
\((b+15)^2\)
- Answer
-
\(b^2 + 30b + 225\)
\((a-10)^2\)
\((x-12)^2\)
- Answer
-
\(x^2 - 24x + 144\)
\((x+20)^2\)
\((y-20)^2\)
- Answer
-
\(y^2 - 40y + 400\)
\((3x + 5)^2\)
\((4x + 2)^2\)
- Answer
-
\(16x^2 + 16x + 4\)
\((6x - 2)^2\)
\((7x - 2)^2\)
- Answer
-
\(49x^2 - 28x + 4\)
\((5a - 6)^2\)
\((3a - 9)^2\)
- Answer
-
\(9a^2 - 54a + 81\)
\((3w - 2z)^2\)
\((5a - 3b)^2\)
- Answer
-
\(25a^2 - 30ab + 9b^2\)
\((6t - 7s)^2\)
\((2h - 8k)^2\)
- Answer
-
\(4h^2 - 32hk + 64k^2\)
\((a + \dfrac{1}{2})^2\)
\((a + \dfrac{1}{3})^2\)
- Answer
-
\(a^2 + \dfrac{2}{3}a + \dfrac{1}{9}\)
\((x + \dfrac{3}{4})^2\)
\((x + \dfrac{2}{5})^2\)
- Answer
-
\(x^2 + \dfrac{4}{5}x + \dfrac{4}{25}\)
\((x - \dfrac{2}{3})^2\)
\((y-\dfrac{5}{6})^2\)
- Answer
-
\(y^2 - \dfrac{5}{3}y + \dfrac{25}{36}\)
\((y + \dfrac{2}{3})^2\)
\((x + 1.3)^2\)
- Answer
-
\(x^2 + 2.6x + 1.69\)
\((x + 5.2)^2\)
\((a + 0.5)^2\)
- Answer
-
\(a^2 + a + 0.25\)
\((a + 0.08)^2\)
\((x - 3.1)^2\)
- Answer
-
\(x^2 - 6.2x + 9.61\)
\((y - 7.2)^2\)
\((b - 0.04)^2\)
- Answer
-
\(b^2 - 0.08b + 0.0016\)
\((f - 1.006)^2\)
\((x + 5)(x - 5)\)
- Answer
-
\(x^2 - 25\)
\((x+6)(x-6)\)
\((x+1)(x−1)\)
- Answer
-
\(x^2 - 1\)
\((t−1)(t+1)\)
\((f+9)(f−9)\)
- Answer
-
\(f^2 - 81\)
\((y−7)(y+7)\)
\((2y+3)(2y−3)\)
- Answer
-
\(4y^2 - 9\)
\((5x+6)(5x−6)\)
\((2a−7b)(2a+7b)\)
- Answer
-
\(4a^2 - 49b^2\)
\((7x+3t)(7x−3t)\)
\((5h−2k)(5h+2k)\)
- Answer
-
\(25h^2 - 4k^2\)
\((x + \dfrac{1}{3})(x - \dfrac{1}{3})\)
\((a + \dfrac{2}{9})(a - \dfrac{2}{9})\)
- Answer
-
\(a^2 - \dfrac{4}{81}\)
\((x + \dfrac{7}{3})(x - \dfrac{7}{3})\)
\((2b + \dfrac{6}{7})(2b - \dfrac{6}{7})\)
- Answer
-
\(4b^2 - \dfrac{36}{49}\)
Expand \((a+b)^2\) to prove it is equal to \(a^2 + 2ab + b^2\).
Expand \((a-b)^2\) to prove it is equal to \(a^2 - 2ab + b^2\).
- Answer
-
\((a-b)(a-b) = a^2 - ab - ab + b^2 = a^2 - 2ab + b^2\)
Expand \((a+b)(a-b)\) to prove it is equal to \(a^2-b^2\).
Fill in the missing label in the equation below.
- Answer
-
First term squared
Label the parts of the equation below.
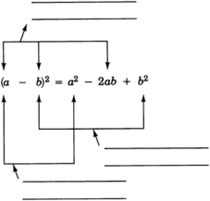
Label the parts of the equation below.
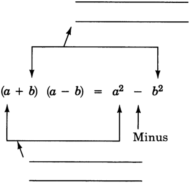
- Answer
-
a) Square the first term.
b) Square the second term and subtract it from the first term.
Exercises for Review
Simplify \((x^3y^0z^4)^5\).
Find the value of \(10^{-1} \cdot 2^{-3}\)
- Answer
-
\(\dfrac{1}{80}\)
Find the product.
\((x+6)(x-7)\).
Find the product.
\((5m - 3)(2m + 3)\)
- Answer
-
\(10m^2 + 9m - 9\)
Find the product.
\((a+4)(a^2 - 2a + 3)\)